数学ガールの第6巻「ポアンカレ予想」がついに発売されましたね。tsujimotterも夢中になって読んでいます*1。
今回の数学ガールのテーマは「ポアンカレ予想」です。「位相空間」や「多様体」といった幾何学のトピックがたくさん登場して、普段は数論ばかりで幾何学に触れてこなかったtsujimotterにとっては、大変勉強になる本となっています。数学ガールを読んで、頭の中が幾何学モードになっています。
さて、本日のブログ記事の主役は 「ド・ラームコホモロジー」 です。ド・ラームコホモロジー、多様体という幾何学的な対象の上で考えられる「微分積分」に深く関連した重要な概念です。以前からブログに書きたいと思っていたのですが、なかなか取りかかれませんでした。せっかく頭が幾何学モードになっているので、熱があるうちにブログにまとめたくなったのです。
「ド・ラームコホモロジー」については、以下の本の3章が大変参考になります。今回の記事の元ネタでもあります。
少し長い話になりますが、面白い内容だと思いますので、ぜひ最後まで読んでもらえると嬉しいです。
0. あらすじ
全体を通して考えたいテーマは「(可微分)多様体上の微分積分」です。高校生くらいまでで習う「微分積分」というのは、ユークリッド空間上の微分積分でした。実は、ユークリッド空間でなくとも、局所的にユークリッド空間とみなされる「多様体」と呼ばれる空間上では、同様に微分積分の理論を組み立てることができます。
この「多様体上の微分積分」における、特に「ド・ラームコホモロジー」という概念について紹介したいと思います。ド・ラームコホモロジーというのは、簡単に言ってしまうと、「多様体上である形をした微分方程式に解が存在するかどうか?」をあらわす群のことです。これは多様体の不変量となっています。
多様体として円周 を考えると、面白いことに、そのド・ラームコホモロジーがフーリエ級数の定数項と関係し具体的に計算できます。
以上のことを理解するためには「多様体」「微分形式」の基本的なことがらを理解する必要があります。この記事では「位相空間ぐらいは知っている」ことを前提に、多様体の基礎的な部分から説明していきたいと思います。
1. (可微分)多様体とは
まずは、今回微分積分を展開する土台となる 多様体 について説明したいと思います。
多様体とは「局所的にはユークリッド空間 の座標によって書ける位相空間
」のことです。
まず
とは一体どういうことでしょうか。これが理解できれば多様体の定義がわかったといっていいでしょう。
は位相空間なので、その開集合をとることができます。1つの開集合をとってきて、
としましょう。
に対して、
のある開集合
への同相写像
があるとします。
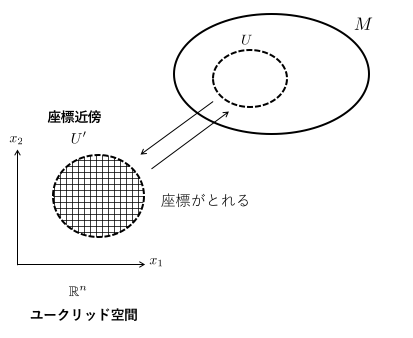
このような状況を考えると、 はユークリッド空間(の開集合)なので、
-座標によって
上の点を表すことができます。
と
は同相なので、同相写像(の逆写像)によって
を
に写すと、
に
-座標が入っているとみなすことができるでしょう。これが「局所的にユークリッド空間
の座標によって書ける」の意味するところです。ユークリッド空間の開集合
を座標近傍といい、その座標系
を局所座標と呼びます。
多様体の定義においては、 上の任意の開集合に対してユークリッド空間が対応する必要はありません。いくつかの代表的な開集合を選んで、それらがユークリッド空間と対応していれば良いのです。ただし、
の任意の点
に対し、
を含む座標近傍が存在することだけは要請されます。つまり、
上の点で、座標によって表せないものは存在しないということです。
次に、 の2つの開集合
を考えましょう。
は共通部分
を持つとします。
には、それぞれ座標近傍としてユークリッド空間の開集合
を割り当てます。
における座標系を
とし、
に対応する座標系を
としましょう。
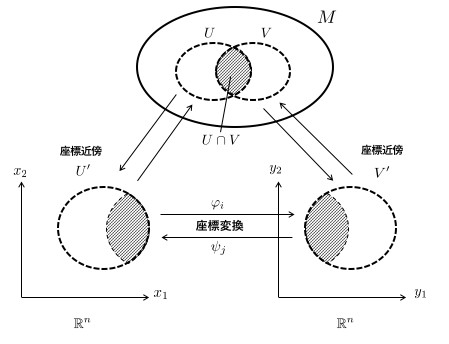
の共通部分
は、
と
という2種類の座標によって記述されています。ここで、
と
の間の「座標変換のルール」を定めましょう。座標変換のルールは、以下のように相互の座標系の間の関係を表す写像
によって定義できます。
この がそれぞれ無限回微分可能であるとき、
の上で微分積分を考えることができます。このような
を
次元可微分多様体といいます。
ここで定義した多様体が、議論の土台となります。まとめると、多様体とは以下の条件を満たすものです:
- 局所的にはユークリッド座標で書くことができる位相空間
- 2つ以上の座標系によって書くことができる部分については、各座標系の変換ルールがあり、そのルールが整合的(具体的には、変換ルールを表す写像が無限回微分可能)
多様体の「こころ」は、なかなか捉えずらいと思っています。(少なくとも)局所的には座標で書けるので、座標を使って議論することできて便利、という感じなのでしょうか。
ところで、これまで散々座標を使って議論してきましたが、この座標という概念はできれば捨て去りたいという気持ちがあります。というのも、座標系に依存した形で微分積分を考えても「多様体上の微分積分」とは言えないからです。変数変換をして変わってしまうような対象は、多様体のものとは言い難いでしょう。そのため、座標を使って定義しておきつつも、最終的には座標を忘れてしまう、という感覚が多様体の理解のポイントだと私は思うのです。この辺の感覚は、議論を進めるにつれて、次第にわかってくるのではないかと思います。
それでは舞台が整ったので、多様体上で「微分」と「積分」を考えていきましょう。
2. 微分形式と定積分
まずは 「微分」 から。今回は簡単のために、 として1次元の多様体を考えたいと思います。1次元の例は、このあとの議論において中心的な役割を果たします。
微分形式(1-形式)
座標近傍を とし、対応する局所座標を
としましょう。すると単純に1変数の微分積分が展開できます。座標変換のルールは、
とします。 上で定義された関数
を考えましょう。
の任意の点を
として、次のように表せます:
しかしながら、この関数の導関数 はうまく定義できないことがわかります。なぜかというと、
は
の座標系で2通りに表せるわけですが、
座標で定義された
の導関数
と、
座標で定義された
の導関数
が一般に一致しないからです。座標の取り方で導関数の値が変わってしまっては、「多様体上の」微分とは認め難いですよね。
そこで、少し考え方を変えて「微分」を定義します。 の2通りの座標をそれぞれ
とするとき、
が成り立ちます。この を
で微分すると
となります。これは、連鎖律と呼ばれるものですね。微分の変換のために という係数がかかっていますが、これがヤコビアンと呼ばれるものです。
この式の両辺に を形式的にかけると、
が得られます。式からわかるように、この量は 座標でも
座標でも同じ値をとります!座標の取り方によらないわけです!よって、多様体における「微分」にふさわしいものといえるでしょう。この
を
の外微分(がいびぶん)といいます。
はそれぞれ
の関数なので、それぞれ
とおきます。すると
という形でかけます。この を
とおいて
と表した式を1次微分形式(略して1-形式)と呼びます。
定積分
今定義した1-形式は、どういう意味を持った量なのでしょうか。
式の形を見ると、局所座標を としたときは「
の関数」に「
」をかけたものになっています。みなさんは「このような形をした式」が積分の中に入っているのを、見たことがあると思います。そう、1-形式は「積分」ができるのです。ここでは1-形式の 「定積分」 をしてみましょう。
今度は1次元として、図を描いてみましょう。
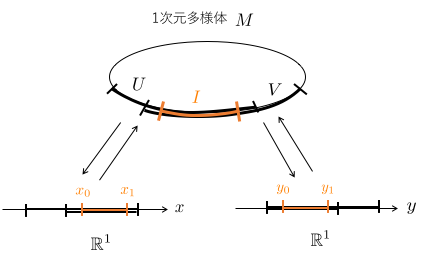
上に閉区間
を考えます。この区間
に沿って、1-形式
を定積分します。
は座標によって
や
のように表されます。
座標で表せれば、今までのように区間を決めて積分ができます。1-形式 の定積分を以下のように計算します:
この定積分は、 で計算しても、
で計算しても同じ値になります。すなわち、座標の選び方によらないものです。そのため、多様体上の1-形式
の、多様体上の区間
における定積分を一意的に定めることができます。
だんだん座標を捨て去る感覚がわかってきましたでしょうか。
0-形式, 2-形式, 3-形式
続いて、0-形式を定義します。0-形式とは、 と表せる式のことです。すなわち関数です。ただし、局所座標の関数というよりは、あくまで多様体上の関数ということに注意する必要があります。
この0-形式 の外微分を考えます。
これは、1-形式になっていることがわかります。すなわち、こういうことです。
ここまでの説明では「0-形式」の意味がまだよくわかりません。0-形式は、1-形式より高次の微分形式からの類推によって理解できます。
実は、1-形式のほかにも、2-形式、3-形式と呼ばれる高次の微分形式が存在します。1-形式では線積分ができたように、2-形式では2重積分、3-形式では3重積分ができます。それらの間には以下のような関係があります。
形式的にみると、0-形式は0重積分ができ、外微分すると1-形式になるものと考えることができます。こう考えると0-形式の位置付けがわかるのではないかと思います。
3. 不定積分
さて、ここまで定積分について考えてきました。定積分という操作は、微分形式から の値を与える関数のようでした。不定積分 は、少し趣きが異なります。
高校数学に戻って考えましょう。1変数関数 の不定積分は、
を満たす原始関数を求める操作でした。
この という式は、
とすると、微分方程式
の解
を求める問題と解釈できます。ここで
は既知の関数で、
は未知の関数です。我々は、与えられた
という手掛かりから、未知の
をどうにかして求めたい。
多様体上で同じ問題を考えるためには、これまで同様、座標系に依存しない形で表す必要があります。 の両辺は座標
で表現されているため、両辺に
をかけます。
このとき、未知変数 を、0-形式
とおきましょう。そして、右辺を1-形式
とおきます。
は与えられていると考えます。
の外微分は、定義から
より、微分方程式は
と書き直すことができました。わかりやすいように、情報を書き加えると
という感じです。よって微分方程式は
と読み替えることができました。もちろん、これは座標には依存しない形で書かれています。
具体例の計算
具体例として、円周 上の不定積分を考えましょう。
は本記事のタイトルにも入っている図形で、今回の中心人物です。以下の式で定義されます:
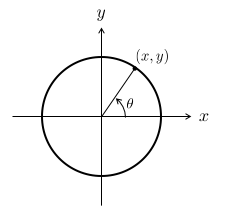
注意したいのは、 は2次元ユークリッド面に埋め込まれているものの、多様体としては1次元だということです。このことは、
という局所座標
を用いることでわかります。
という1変数で表せていますので、1次元多様体です。
さて、与えられた1-形式として とします。0-形式
に関する微分方程式
を解いてみましょう。
0-形式 とすれば、微分方程式は
と同値であることがわかります。
を代入すると
が成り立つからです。
したがって、 を積分すると
となります。
一方で、0-形式 は
上の関数でした。
上の関数ということは、局所座標
で考えると周期を持たなければなりません。すなわち、
を満たす必要があります。
ところが、先ほど求めた は、この条件を満たしません。したがって、微分方程式
は解を持たないことがわかります。
今回は 上の微分方程式
を考えましたが、もし
上だったらどうでしょう。この場合は、周期による制約はありませんから、そのまま
が解となります。微分形式で表すと、
が微分方程式
の解となります。
と
における結果の違いは、まさに
と
が同相でないことの証明にもなります。実は、このアイデアこそが、ド・ラームコホモロジーの考えのもとになっているのです。
4. ド・ラームコホモロジー
多様体を としたとき、
上の微分方程式を考えて、その解の「ある・なし」によって
を捉えよう、というのが ド・ラームコホモロジー のアイデアです。
ここでは一般に を
次元可微分多様体とします。先ほどのように微分方程式
を考えます。ここで、 は未知の
-形式、
を与えられた
-形式とします。この
の与え方によって、式
は解を持ったり持たなかったりするわけです。
ここで考えたいのは、式 のような微分方程式全体を考えたときに、解を持つものはどの程度あるのか、という問題です。この問題を定量化して考えるために、
という集合を定義します。
まず、 上の
-形式全体を
とします。この
の中で、式
の微分方程式が解を持つような
全体の集合
を考えます。言い換えると
と書くことができるでしょう。
もう一つ、 を以下で定義します。
これはイメージしづらいかもしれませんので、少し説明します。-形式
は外微分をとると
-形式になります(0-形式を外微分すると1-形式になったように)。この
-形式
が 0 になるような
をすべて集めてくるということです。
さて、こうして得られた は、すべて
-ベクトル空間となっています。また、次のような包含関係があります:
右側の包含関係は少し考える必要があります。 としたとき、
の定義から
を満たす
-形式
が存在します。したがって
が成り立ちます。最後の等式は、微分形式に外微分 を2回作用させると 0 になるという一般論からわかります。よって、
は
にも含まれます。
要するに、次の図のような包含関係が得られたということです。
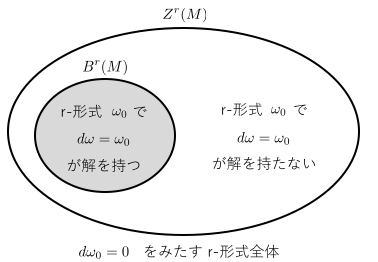
よって、
という量を考えることに意味が出てきます。これを 次ド・ラームコホモロジー群と呼びます。
これはまさに、微分方程式 が解を持つような
-形式に対して、解を持たない
-形式が相対的にどの程度あるのかを、定量的に表す指標になっていると言えます!
上のすべての
-形式
が
に解を持てば
となります。そうでなければ
です。
早速具体例を計算してみましょう。
具体例の計算
と
を考えます。どちらも1次元多様体なので、任意の1-形式は外微分すると0になることに注意します。したがって
となります。つまり、1-コサイクルとしてすべての1-形式を考えてよいということですね。
M = R の場合:
ここから場合分けを行います。まず、 の場合からです。前節で議論したように、
上の任意の微分可能な関数
には、原始関数
が存在します。よって、
となり、両辺に をかけると
です。右辺は与えられた1-形式 で、左辺の
を未知の0-形式
とすると
という微分方程式を満たします。 として任意の関数を考えてよいので、
も任意の1-形式です。したがって、任意の1-形式
に対して、上記の微分方程式を満たす解
が存在することがわかりました。よって
これより、1次ド・ラームコホモロジーは
と得られます。あとで の結果と比較してみてください。
M = S^1 の場合:
前節の計算では、 としたときの
は解を持ちませんでした。したがって、ざっくり考えるのであれば
であり、
となることがただちにわかります。
さて、 と
では、それぞれのド・ラームコホモロジー群が同型ではないことがわかりました。ド・ラームコホモロジーには
という性質があるので、対偶をとれば と
が同相でないことがわかります。面白いですね。
5. フーリエ級数と1次ド・ラームコホモロジー
の1次ド・ラームコホモロジーをもう少し詳しく計算してみましょう。
前節では1-形式として だけを考え、
が解を持つかどうか考えました。ここでは、任意の1-形式
に対して微分方程式が解を持つか考えたいのです。
上の任意の1-形式は、
上の任意の関数
を用いて
と表されます。よって、
上の任意の関数を考えたい。
上の任意の関数
は、周期
を持つのでした。このような形の任意の関数を表す方法を我々は知っています。フーリエ級数 です。
周期 を持つ任意の関数
は、フーリエ級数の理論によって、次のように表すことができます:
ここで、 です。
式 で表される関数
を用いてつくられる1-形式
に対して、微分方程式
が解を持つかどうかを考えたい。 は0-形式なので
とおくと、
も式
の形で表される関数です。
議論を単純化するために、式 を前半と後半に分けて考えましょう:
まず、後半だけを考えて とします。このとき
として
というものを考えましょう。これは 上の0-形式になっていますね。
を外微分すると
となり、 と一致します。 よって、後半部分だけを考えた
は微分方程式
の解を持つことがわかりました。
次に、前半だけを考えて としましょう。
の関数
は、微分すると定数項が 0 になってしまいます。したがって、
としてどのような関数を持ってこようとも、
であれば、
とできないことがわかります。よって、 全体における微分方程式に解がない部分は、本質的に定数項
の部分であることがわかります。
よって、1次ド・ラームコホモロジーは
となります。これで、 の1次ド・ラームコホモロジーが完全に決定できました。
これまでの計算からわかることは、フーリエ級数の定数項が における1次ド・ラームコホモロジーを表しているということですね。これは面白いなと思いました。
6. おわりに
今日は、ド・ラームコホモロジーについて紹介しました。ド・ラームコホモロジーは、解が存在しない微分方程式が解が存在するものと比べてどれぐらいあるかを表す群で、多様体上の微分積分における重要な不変量です。さらに、 上のド・ラームコホモロジーを計算するときに、フーリエ級数の理論が使えるという話もしました。実は、フーリエ級数の定数項が、
のド・ラームコホモロジーを決めていたというのです。
さて、せっかく頑張って説明してきたので、最後に少し発展的な話をしたいと思います。今回は微分方程式の解の存在を直接調べましたが、もう少し簡単にド・ラームコホモロジーを決定する方法があります。
今までは多様体 上の開区間における積分を考えていましたが、ホモロジー上で自然な積分を考えることができます。すると、ド・ラームコホモロジーの元
をホモロジー
で積分する
といったことが可能になります。この式は、ド・ラームコホモロジー群とホモロジー群の「非退化なペアリング」になっていて、結果として
なる -ベクトル空間としての同型が得られます。これをド・ラームの定理といいます。
右辺のホモロジー(の双対なのでコホモロジー)は、図形の形から計算することができます。一方、左辺は微分方程式の解の存在を頑張って調べないと計算できません。
今回のケースにおいては とすると、右辺は
の形から
とすぐわかるので、 ド・ラームコホモロジーを簡単に計算することができます。面白いでしょう。
ド・ラームの定理は「微分方程式の解の存在は、舞台となる多様体の形からわかる」ということを主張していると思います。逆に、多様体のことを知りたければ、その上の微分方程式を考えよ、と言っているようにも見えます。微分方程式の構成要素は、関数(0-形式)と微分形式。つまり、多様体上の関数や微分形式が、舞台となる多様体そのものの情報を持っているというのですね。こうした話としては、これまでも聞いたことはありましたが、今回の勉強でようやく実感できたかもしれません。
それでは今日はこの辺で。
ずいぶんと長文になってしまいましたが、最後までお付き合いありがとうございました。
*1:tsujimotterは数学ガールの大ファンで、全巻持っています。札幌に住んでいた頃(ちょうど第5巻が発売された頃ですが)は、数学ガール読書会なるイベントを開いたこともありました

