無理関数の不定積分と双曲線、微分形式

今日考えたいのは、

$\displaystyle \int \frac{1}{\sqrt{x^2 + 1}} dx$ 　や　 $\displaystyle \int \sqrt{x^2 + 1}\, dx$

というタイプの積分です。

いわゆる無理関数の積分と呼ばれるもので、大学受験でも難関大学の問題として登場するみたいですね。

今回の記事のきっかけとなったのは、清さんによる以下のツイートです：

【清史弘からの提案 7 】
　教育系YouTuber の人に向けて、このような動画はどうですか? という内容です。もちろん、YouTuber でない方もご参加ください。
　私の考え方は24時間以内にあげようと思っています。
　これは、唯一の正解というよりは、いろいろとあってよいと思います。#清史弘からの提案 pic.twitter.com/UokREtslQt
— 清　史弘 (@f_sei) 2020年9月13日

上のツイートによると、今回の積分は

$t = x + \sqrt{x^2 + 1} \tag{1}$

という変数変換がキーになるようですが、いったいどこからこの式が現れたのか説明せよ、というのが問題です。

清さんのツイートの引用リツイートに、加藤文元先生がこんな意味深なツイートを残されています：

大学教科書ですが、これ私の教科書には書きました（数研講座大学教養微分積分 p.146）。代数関数の積分が有理関数の積分に帰着できるか否かには、代数曲線論による少し深い背景があるという話ですが、逆に言えば、どういうときにはそういう変数変換が不可能かということもわかります。 https://t.co/pw4Ap7taX3
— Fumiharu Kato 加藤文元（Bungen） (@FumiharuKato) 2020年9月13日

どうもこの積分には深い数学的背景があるようです。このツイートを見てtsujimotterは面白そうだと思いました。

実際、代数曲線論に基づく議論によって、上記の変数変換で積分が解けることを説明できそうです。このことについてまとめてみようとおもいます。

清さんの元々の問題は受験生を対象とした説明を想定されていて、私が理解した内容はそれを大きく超えてしまっています。

したがって、今回の記事の内容は 受験生の役に立つものではありません。上の問題の答えというわけでもありません。それでも面白そうなので、せっかくだからまとめてみようというのが本記事の趣旨です。よろしければご覧いただければ幸いです。

また、今回の内容は、特にどこかに書いてあった話というわけではなく、私が今まで見聞きした情報を元に「多分こうだろう」と思って書いた内容になります。内容の正確性は保証できませんので、その点ご了承いただければと思います。

まず普通に解いてみよう

まずは、式 $(1)$ の変数変換を用いて積分を解いてみましょう。

$\displaystyle I = \int \frac{1}{\sqrt{x^2 + 1}} dx \tag{2}$

の方が簡単なので、こちらからまず解いてみたいと思います。

$\displaystyle \int \sqrt{x^2 + 1} dx$ の方は、記事の最後に解法が書かれたページへのリンクを紹介します。こちらの積分も、部分積分によって $\displaystyle \int \frac{1}{\sqrt{x^2 + 1}} dx$ の積分に帰着させることになります。

$t = x + \sqrt{x^2+1}$ とおき、 $x$ で微分すると

$\displaystyle \frac{dt}{dx} = 1 + \frac{1}{2}\cdot \frac{2x}{\sqrt{x^2 + 1}} = 1 + \frac{x}{\sqrt{x^2 + 1}} = \frac{\sqrt{x^2 + 1} + x}{\sqrt{x^2 + 1}} = \frac{t}{\sqrt{x^2 + 1}}$

と計算できます。したがって

$\displaystyle \frac{dt}{t} = \frac{dx}{\sqrt{x^2 + 1}}$

という関係が得られます。

これにより、式 $(2)$ の積分は

$\displaystyle I = \int \frac{1}{\sqrt{x^2 + 1}} dx = \int \frac{dt}{t}$

のように計算できますね。右辺は明らかに積分できる形になっていますので、さらに計算を進めると

$\displaystyle \begin{align} I &= \int \frac{dt}{t} \\ &= \log |t| + C \\ &= \log |x + \sqrt{x^2 + 1}| + C \end{align}$

とすることができます。 $C$ は積分定数です。最後の等式では、 $t = x + \sqrt{x^2 + 1}$ を再度代入していることに注意しましょう。

ポイントは、求めたい積分を $\displaystyle \frac{1}{t}$ という有理関数の積分に帰着できたことですね。

しかし、うまいこと計算できたものの、これでなぜうまくいくのかはよくわかりませんね。

双曲線を考える

上の積分の変数変換 $t = x + \sqrt{x^2 + 1}$ の意味するところを考えてみましょう。一体なぜこのような変換を考えたらうまくいくのでしょうか。

最初のアイデアは双曲線を考えるということです。被積分関数

$\displaystyle \frac{1}{\sqrt{x^2 + 1}}$

の分母 $\sqrt{x^2 + 1}$ を $y$ と置くことにします。すると

$y = \sqrt{x^2 + 1}$

となりますが、両辺を2乗してから移項すると

$y^2 - x^2 = 1$

となります。これはまさに双曲線の方程式となっていますね。双曲線のグラフは次のようになります。

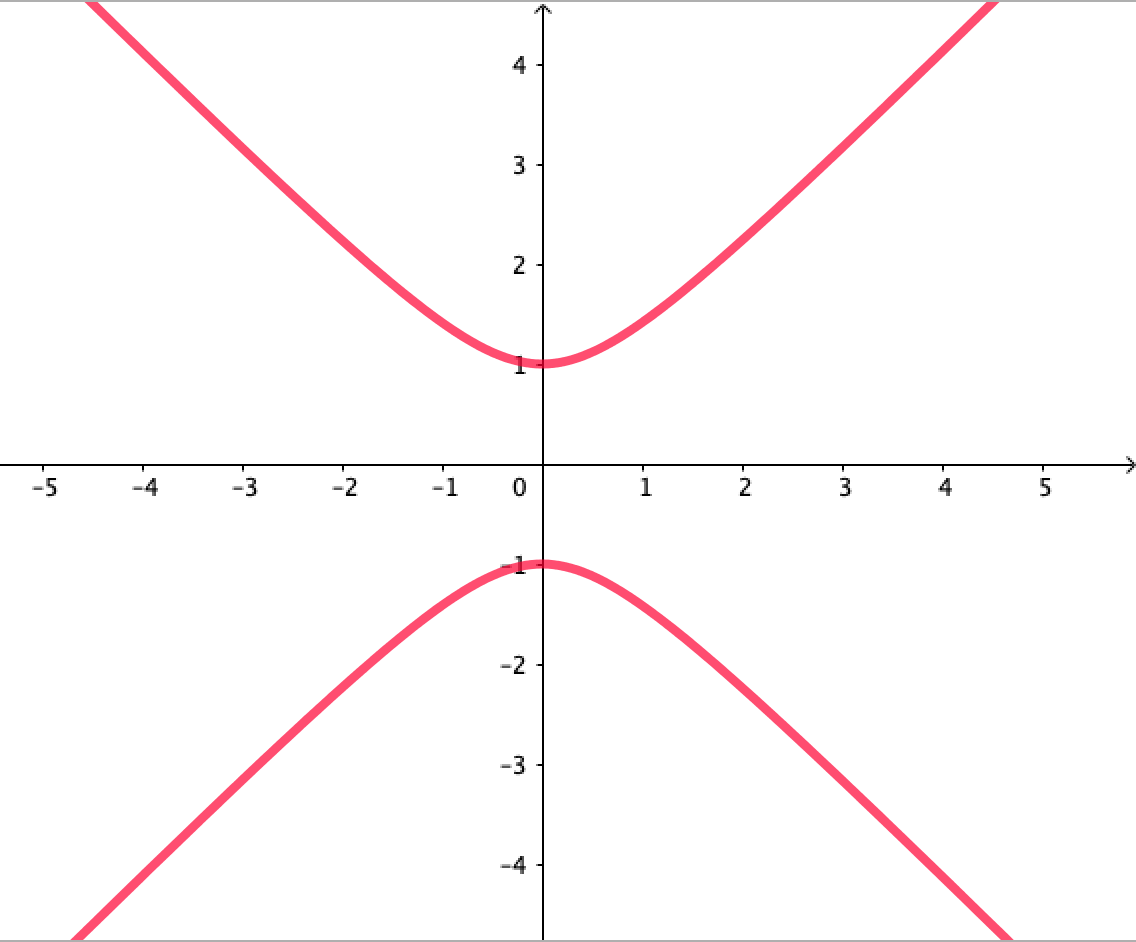
f:id:tsujimotter:20200914215934p:plain:w300

言い換えると、被積分関数は

$\displaystyle \frac{1}{\sqrt{x^2 + 1}} = \frac{1}{y}$

という関数ですが、これは2変数 $x, y$ の関数であり、その変数の間には $y^2 - x^2 = 1$ という関係式があるわけですね。

すなわち、双曲線上の関数（双曲線上の点に対して値が定義された関数）だと思えるというわけです。

双曲線には媒介変数（パラメータ）表示がありました。具体的には、 $\theta$ という変数に対して、2つの双曲線関数 $\sinh, \cosh$

$\displaystyle \sinh \theta = \frac{1}{2}(e^{\theta} - e^{-\theta})$

$\displaystyle \cosh \theta = \frac{1}{2}(e^{\theta} + e^{-\theta})$

を考えます。これらの関数には

$\cosh^2 \theta - \sinh^2 \theta = 1$

という関係が成り立ちます。

実際、

$\cosh \theta + \sinh \theta = e^{\theta}$

$\cosh \theta - \sinh \theta = e^{-\theta}$

と計算できますので、

$\cosh^2 \theta - \sinh^2 \theta = (\cosh \theta + \sinh \theta)(\cosh \theta - \sinh \theta) = e^{\theta}e^{-\theta} = 1$

となり、目的の関係式が得られます。

この関係式は、まさに双曲線の方程式そのものです。実際、 $y = \cosh \theta, \;\; x = \sinh \theta$ とおけば

$y^2 - x^2 = 1$

となり、今回の双曲線が現れます。 $\theta$ を動かすことで、双曲線の点に対応させることができ、

$\begin{cases} x = \sinh\theta = \frac{1}{2}(e^{\theta} - e^{-\theta}) \\ y = \cosh\theta = \frac{1}{2}(e^{\theta} + e^{-\theta}) \end{cases}$

を双曲線 $y^2 - x^2 = 1$ の媒介変数表示といいます。

三角関数でも

$\cos^2 \theta + \sin^2 \theta = 1$

という式が成り立ち、ここから $x = \cos \theta, \;\; y = \sin \theta$ とすることで円の媒介変数表示が得られますが、それと同じことをやっているわけですね。

媒介変数表示において、 $e^\theta$ という形の式がたくさん現れますので、 $t = e^\theta$ と置いてみましょう。すると

$\begin{cases} x = \frac{1}{2}\left(t - \frac{1}{t}\right) \\ y = \frac{1}{2}\left(t + \frac{1}{t}\right) \end{cases}$

となります。つまり、パラメータとして $\theta$ を動かす代わりに $t$ を動かすことにするのです。

唐突ではありますが、ここで $x + y$ を計算します：

$\displaystyle x + y = \frac{1}{2}\left(t - \frac{1}{t}\right) + \frac{1}{2}\left(t + \frac{1}{t}\right) = t$

つまり $t = x + y$ が言えたのですが、この $y$ は元々 $y = \sqrt{x^2 + 1}$ だったわけなので、代入すると

$t = x + \sqrt{x^2 + 1}$

です。

あれ、これどこかで見覚えがある式ですね。

そう、元々の積分を計算するための変数変換の式そのものになっています！　こんなところに出てくるとは！

もう少しだけ背景が理解できるように、代数曲線の言葉を導入して言い換えを行います。

また、円の媒介変数表示を思い出しますが、パラメータ $t$ に対して　

$\displaystyle t \longmapsto \left(\frac{1 - t^2}{1 + t^2}, \; \frac{2t}{1 + t^2}\right)$

という対応を考えると、単位円の座標を表示することができるのでした。これは変数 $t$ で表される「1次元の直線」から、座標 $(x, y)$ で表される単位円 $x^2 + y^2 = 1$ に対する対応関係を与えていると考えられます。

コンパクトな図形である円に対応させるにあたって、実際は「1次元の直線」としては射影直線 $\mathbb{P}^1$ を考えることになります。（射影直線について知らない方は、通常の直線に無限遠点 $\infty$ を加えてできる直線だと思っていただければと思います。）

同様にして、先ほどの双曲線の媒介変数表示も、射影直線から双曲線 $C\colon y^2 - x^2 = 1$ への有理写像

$\begin{align} \phi \colon \mathbb{P}^1 &\longrightarrow C \\ t &\longmapsto \left( \frac{1}{2}\left(t - \frac{1}{t}\right), \; \frac{1}{2}\left(t + \frac{1}{t}\right) \right)\end{align}$

を与えていると考えることができます。値域の座標が、定義域の変数の有理式で表されるような写像のことを有理写像といいます。

さて、この写像は逆を考えることもできます。実際、 $t = x + y$ が成り立つので

$\begin{align} \psi \colon C &\longrightarrow \mathbb{P}^1 \\ (x, y) &\longmapsto x + y \end{align}$

という有理写像も考えることができます。
（つまり、 $\psi(x, y) = x + y \in \mathbb{P}^1$ なので、 $C$ の任意の点 $(x, y)$ に対して $\mathbb{P}^1$ の点を対応づけることができます。）

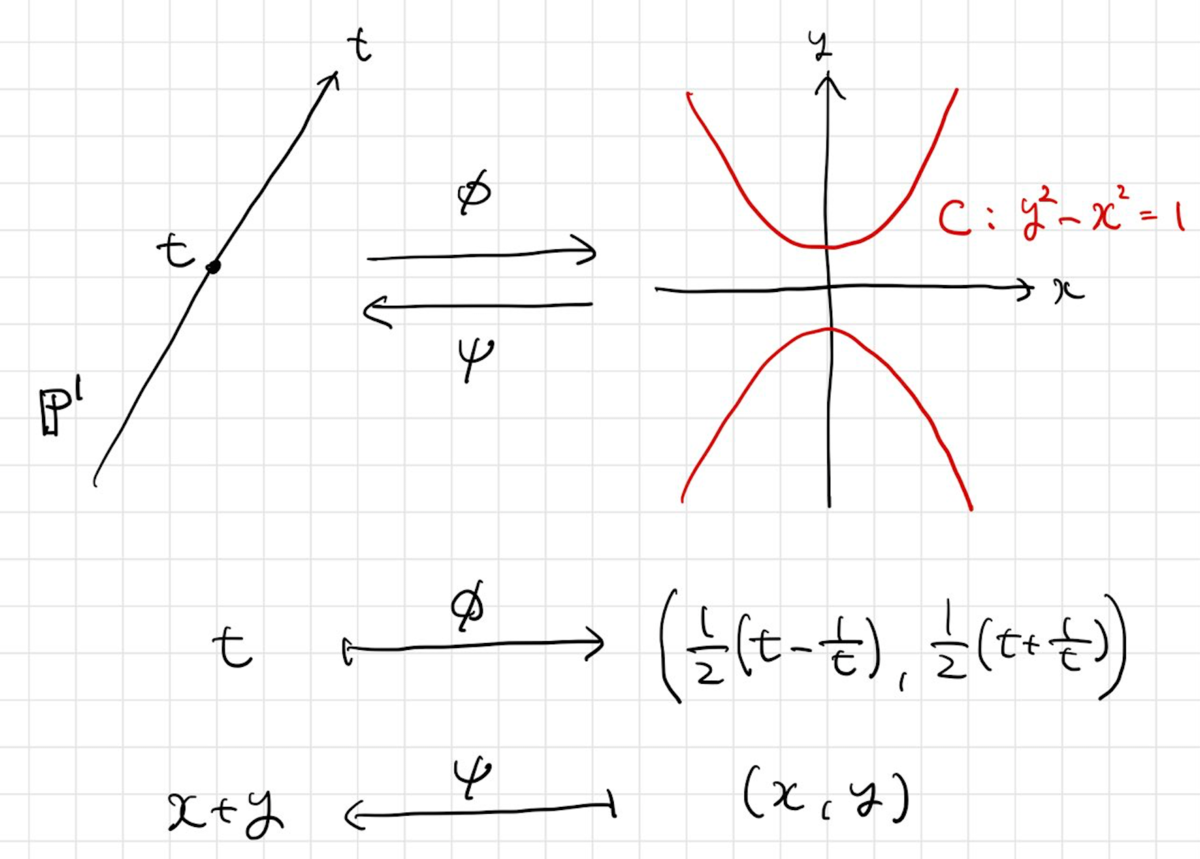
f:id:tsujimotter:20200914220426p:plain:w400

これらの有理写像の合成を考えると、有限個の点を除いて

$\psi \circ \phi = \operatorname{id}_{\mathbb{P}^1}$

$\phi \circ \psi = \operatorname{id}_{C}$

となることを確認することができます。
（「有限個を除いて」といったのは、 $\phi$ は $t = 0$ で定義できないので、それを除いたところでは逆写像になっているということです。有理写像は、有限個の点を除いて定義されていれば問題ないことを補足しておきます。）

一般に、2つの曲線 $C_1, C_2$ の間の有理写像 $\phi \colon C_1 \to C_2, \; \psi \colon C_2 \to C_1$ が有限個の点を除いて互いに逆写像になっているとき、 $\phi, \psi$ は双有理写像であるといいます。また、 $C_1, C_2$ は双有理同値であると言います。

何が言いたかったかというと、射影直線 $\mathbb{P}^1$ と双曲線 $C \colon y^2 - x^2 = 1$ の間には双有理写像が存在し、その変換則がまさに積分のときに用いた変数変換だったというわけです。

代数曲線上の微分形式

ここからは、少しだけ抽象的な話になります。

曲線 $C$ に対して $K$ をその定義体（定義方程式の係数が $K$ の元ということ）とし、その代数的閉包を $\overline{K}$ とします。代数的閉包の意味がわからなくても、 $K = \mathbb{C}, \; \overline{K} = \mathbb{C}$ みたいな状況を考えてもらえれば十分です。

$C$ の変数 $x, y$ を用いた有理式は、 $x, y$ に $\overline{K}$ の値を代入することで、 $C$ から $\overline{K}$ への関数だと思うことができます。このような関数全体の集合は体をなしますが、これを $C$ 上の関数体といい $\overline{K}(C)$ と表します。

$C\colon y^2 - x^2 = 1$ として、たとえば

$\begin{align} f(x, y) &= \frac{1}{x+y} \\ g(x, y) &= x^2 + y^2 - 1 \\ h(x, y) &= \frac{1}{y} \end{align}$

みたいな関数が $\overline{K}(C)$ の元です。もちろん、単なる $x$ や $y$ といった変数そのものも $C$ 上の関数なので、 $\overline{K}(C)$ の元であることに注意します。

一つ注意したいのは、 $y^2 = x^2 + 1$ という関係式があるので、 $y$ の次数を1次以下に正規化できるということです。たとえば $y^5$ という式も

$y^5 = y(x^2 + 1)^2$

という形になり、 $y$ についての1次式にすることができました。（この場合、xについての次数は1次以下になるとは限りません。）

$\overline{K}(C)$ は $\overline{K}(x)$ に $y$ を添加した拡大体と思うことができますが、 $y^2 = x^2 + 1$ の関係により、 $\overline{K}(C)$ は $\overline{K}(x)$ 上の2次拡大体であることがわかります。一般に、 $\overline{K}(x)$ 上の有限次拡大体を（1変数）代数関数体といいます。

今回話す内容は、代数関数体の理論と言ったりするようです。

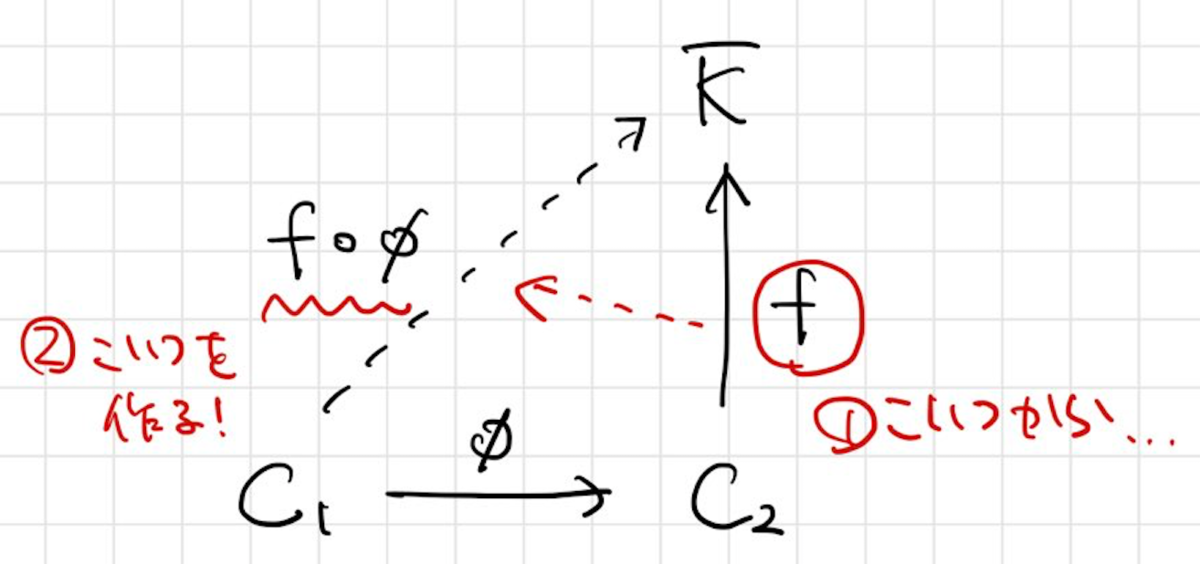
$K$ 上定義された2つの曲線 $C_1, \; C_2$ の間に有理写像 $\phi \colon C_1 \to C_2$ が与えられたときに、関数体 $\overline{K}(C_1), \; \overline{K}(C_2)$ の間にも「逆方向の」写像 $\phi^*$ が次のように定義されます：

$\begin{align} \phi^*\colon \overline{K}(C_2) &\longrightarrow \overline{K}(C_1), \\ f &\longmapsto f\circ \phi \end{align}$

この $\phi^*$ を $\phi$ の引き戻しといいます。

引き戻しについてもう少しだけ補足します。 $\overline{K}(C_2)$ の元 $f$ は

$C_2 \xrightarrow{f} \overline{K}$

という写像です。これに $\phi\colon C_1 \to C_2$ を合成すると

$f\circ\phi\colon C_1 \xrightarrow{\phi} C_2 \xrightarrow{f} \overline{K}$

という写像が得られますが、これは $C_1$ から $\overline{K}$ への写像です。すなわち、 $f\circ\phi \in \overline{K}(C_1)$ ということです。 $\phi^* f = f \circ \phi$ ということですね。

f:id:tsujimotter:20200914221052p:plain:w300

考えてみればただの合成なのですが、ややこしいので、わからなくなったらここに立ち返ることにしましょう。

続いて、微分形式を定義します。曲線 $C$ 上の任意の関数 $f \in \overline{K}(C)$ に対して $\newcommand{\d}{{\mathrm d}} \d$ という演算をつけて得られる $\d f$ を考えます。任意の $\d f$ によって生成される $\overline{K}(C)$ ベクトル空間 $\Omega_C$ であって、次の4つの演算ルールを満たすものを考えます：

$\d (f + g) = \d f + \d g, \;\; (f, g \in \overline{K}(C) )$
$\d (af) = a \,\d f, \;\; (a \in \overline{K},\; f \in \overline{K}(C) )$
$\d (fg) = g \,\d f + f \,\d g, \;\; (f, g \in \overline{K}(C) )$
$\d a = 0, \;\; (a \in \overline{K} )$

1、2のルールが線型性です。3つめはライプニッツルールといって、積の微分法則をモデル化したもので、微分形式を特徴付けるルールですね。4つめは定数が0になるというルールですね。これもまさに「微分」的なルールですね。

要するに、 $f_i, g_i \in \overline{K}(C)$ に対して

$\displaystyle \sum f_i \, \d g_i$

というような元全体を考えたいということですね。これを $C$ 上の微分形式といいます。 $\Omega_C$ は微分形式のなす $\overline{K}(C)$ ベクトル空間ということです。

2つの曲線 $C_1, C_2$ に対して対応する微分形式全体のベクトル空間 $\Omega_{C_1}, \; \Omega_{C_2}$ がそれぞれ定義されます。有理写像 $\phi \colon C_1 \to C_2$ に対して、微分形式の間にも引き戻し写像が同様に定義されます：

$\begin{align} \phi^* \colon \Omega_{C_2} & \longrightarrow \Omega_{C_1}, \\ \sum f_i \, \d g_i &\longmapsto \sum \left(\phi^* f_i \right) \, \d\left(\phi^* g_i\right)\end{align}$

関数に対して引き戻し、つまり $\phi$ を合成すればいいわけですね。

これが言いたかったことなのですが、有理写像 $\phi \colon C_1 \to C_2$ があれば、引き戻しとして $\phi^* \colon \Omega_{C_2} \to \Omega_{C_1}$ なる写像を作ることができます。これにより、 $C_2$ 上の微分形式から $C_1$ 上の微分形式を作ることができるというわけです。

さて、長かったですが、元々の問題に戻りましょう。前節までの議論により、射影直線 $\mathbb{P}^1$ と双曲線 $C\colon y^2 - x^2 = 1$ の間には

$\displaystyle \begin{align} \phi \colon \mathbb{P}^1 &\longrightarrow C \\ t &\longmapsto \left(\frac{1}{2}\left(t - \frac{1}{t}\right), \; \frac{1}{2}\left(t + \frac{1}{t}\right) \right)\end{align}$

という有理写像があるのでした。

求めたい積分は $C$ 上の微分形式

$\displaystyle \frac{1}{y} \d x \in \Omega_C$

の積分でした。

これに対して $\phi$ の引き戻し $\phi^*$ を当てることで、 $\mathbb{P}^1$ 上の微分形式を得ることができるというのが上で述べた一般論でした。実際に計算してみましょう。

その前にライプニッツルールの応用として、商の微分を計算しておきます。 $f/g$ の微分は次のように計算されます：

$\displaystyle d\left(\frac{f}{g}\right) = \frac{g\,df - f\,dg}{g^2}$

$h = f/g$ とおくと $gh = f$ です。したがって

$df = d(gh) = h\,dg + g\,dh$

より

$\displaystyle dh = \frac{df - h\,dg}{g} = \frac{df - \frac{f}{g}\,dg}{g} = \frac{g\,df - f\,dg}{g^2}$

となります。よって

$\displaystyle d\left(\frac{f}{g}\right) = \frac{g\,df - f\,dg}{g^2}$

が得られます。

これを使って

$\displaystyle \phi^*\left( \frac{1}{y} \d x \right)$

を計算しましょう。

微分形式の引き戻しの定義より

$\displaystyle \phi^*\left( \frac{1}{y} \d x \right) = \phi^*\left( \frac{1}{y}\right) \d \left( \phi^* x \right)$

となります。

$\displaystyle \phi^*\left( \frac{1}{y}\right) = \frac{1}{\frac{1}{2}\left(t + \frac{1}{t}\right)}$

$\displaystyle \phi^* x = \frac{1}{2}\left(t - \frac{1}{t}\right)$

であるから

$\displaystyle \phi^*\left( \frac{1}{y} \d x \right) = \frac{1}{\frac{1}{2}\left(t + \frac{1}{t}\right)}\frac{1}{2} \d \left(t - \frac{1}{t}\right)$

ここで、商の微分やライプニッツルールを使って

$\displaystyle \d \left(t - \frac{1}{t}\right) = \d \left(\frac{t^2 - 1}{t}\right) = \frac{t \d(t^2) - (t^2 - 1) \d t}{t^2} = \frac{2t^2 \d t - (t^2 - 1) \d t}{t^2} = \frac{t^2 + 1}{t^2}\d t$

が得られます。

結局

$\displaystyle \phi^*\left( \frac{1}{y} \d x \right) = \frac{1}{\frac{1}{2}\left(\frac{t^2 + 1}{t}\right)}\frac{1}{2} \frac{t^2 + 1}{t^2}\d t = \frac{1}{t}\d t$