多様体の「接ベクトル空間」の一歩手前の話

最近、多様体に関する勉強をしているのですが「接ベクトル空間」という概念を習得するのに苦労しています。ちょっと抽象的すぎてよくわからないなと思っていたところに、黒木玄さんからの次のツイートが。

#数楽伝統的なスタイルでは、まず古典的なℝ³内の曲面論についての講義があって、その一般化として多様体論の講義が続く。

曲面のパラメータ表示 (u,v)↦𝐩(u,v) の偏微分作られる接ベクトル達 ∂𝐩(u,v)/∂u, ∂𝐩(u,v)/∂v の𝐩(u,v)を略したものが ∂/∂u, ∂/∂v だと、思うこともできます。
— 黒木玄 Gen Kuroki (@genkuroki) 2021年1月28日

というわけで、 $\mathbb{R}^3$ に埋め込まれた2次元曲面（ $2$ つの変数でパラメータ表示された図形）を考えて、その1点 $P$ に接する平面について考えてみましょう。これは多様体そのものではありませんが、実際このような古典的な対象の計算を考えてみることで、多様体の接ベクトル空間がどうしてそのような定義なのか、理解できた気がします！

今回、多様体や多様体の接ベクトル空間の定義は与えませんが、多様体の勉強をしている人はぜひご自身の本の定義と見比べて考えていただければ幸いです。

注意：
今回の記事はtsujimotterが勉強中の内容を自分の言葉でまとめてみたものになります。正しさは保証できませんので、その点にご了承ください。間違っているところなどありましたら、勉強になりますのでご指摘いただければと思います。

曲面のパラメータ表示と方向ベクトル

曲面をパラメータ表示することを考えましょう。 $\mathbb{R}^2$ から $\mathbb{R}$ への関数 $x, y, z$ を考えます。この $x, y, z$ はそれぞれ無限回偏微分でき、その結果が連続であると仮定しましょう。こういう関数のことを $C^\infty$ 級関数といいます。

この3つの関数を使って、パラメータ $(u, v) \in \mathbb{R}^2$ を動かしたときに

$p(u, v) := (x(u, v), \; y(u, v), \; z(u, v) )$

が描く $\mathbb{R}^3$ 内の図形を考えます。こういう図形を曲面と言いますね。

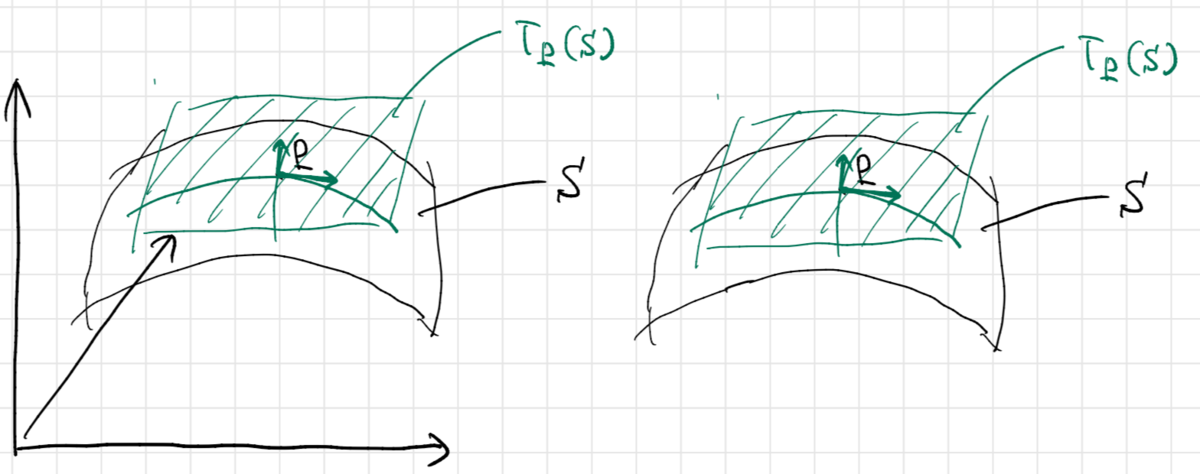
この曲面を $S$ とし、 $S$ 上の任意の1点 $P$ を固定します。点 $P$ のパラメータ $u, v$ における座標を $a, b$ とします。つまり、 $P = p(a, b)$ ということです。この点 $P$ で $S$ に接する面（これを接平面といいます）を考えたいと思います。

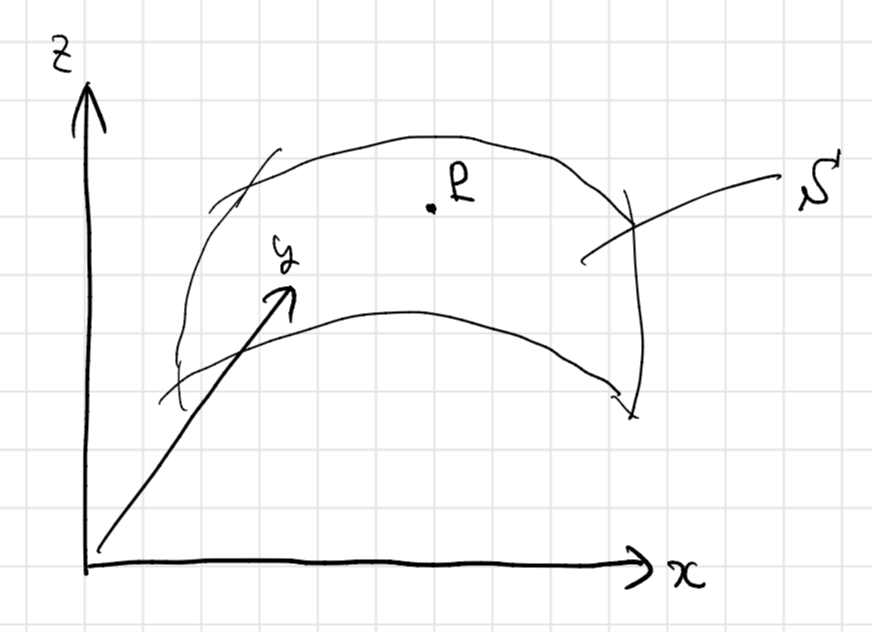
f:id:tsujimotter:20210203092826p:plain:w300

そもそも「接平面」の定義とは何でしょうか？

ここでは、こんな風に考えましょう。 $S$ 上の点 $P$ を通る曲線 $C$ を考えて、点 $P$ での $C$ の接線を求めます。このような任意の曲線に対する接線が同一の平面内を通るとき、これを点 $P$ における接平面と呼ぶことにするのです。

そんなわけで、 $S$ 上の点 $P$ を通る曲線を考えたいと思いますが、一番分かりやすい曲線を考えましょう。 $p(u, v)$ における変数 $v$ を固定して $u$ だけ動かすと、これは $S$ 上の曲線になりますね。この曲線を $C_u$ とします。

この曲線 $C_u$ の点 $P$ における接線の方向ベクトルは

$\displaystyle \frac{\partial p}{\partial u}(P) = \left(\frac{\partial x}{\partial u}(a, b), \frac{\partial y}{\partial u}(a, b), \frac{\partial z}{\partial u}(a, b) \right) \tag{1}$

になるのはよいでしょうか。

同様に、点 $P$ を通る曲線として、 $p(u, v)$ の $u$ を固定して $v$ だけ動かして得られる曲線 $C_v$ を考えます。 $C_v$ の点 $P$ における接線の方向ベクトルは

$\displaystyle \frac{\partial p}{\partial v}(P) = \left(\frac{\partial x}{\partial v}(a, b), \frac{\partial y}{\partial v}(a, b), \frac{\partial z}{\partial v}(a, b) \right) \tag{2}$

となります。

上の２つの曲線 $C_u, C_v$ および方向ベクトルはあとで重要な役割を果たすので、覚えておいてください。

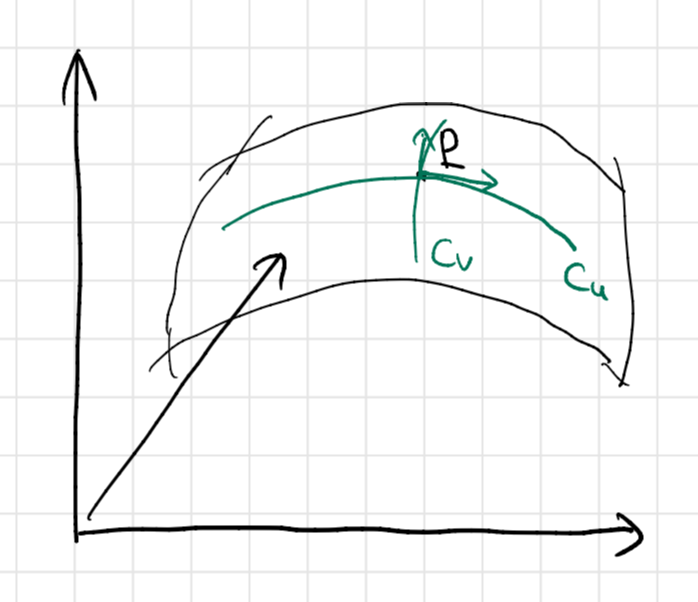
f:id:tsujimotter:20210203092920p:plain:w300

もう少し一般的に $S$ 上の任意の曲線を考えたいと思います。実数 $\mathbb{R}$ の $0$ を含む適当な開区間 $(-\varepsilon, \varepsilon)$ の点 $t$ に対して、パラメータ $u, v$ を与える $C^\infty$ 級関数 $u(t), v(t)$ を考えます。さらに

$\phi(t) = p(u(t), v(t)) = ( x(u(t), v(t)), y(u(t), v(t)), z(u(t), v(t)) )$

を考えます。つまり、時刻 $t$ に応じて、曲線上の点の座標を与える関数というわけですね。また、

$\phi(0) = p(u(0), v(0)) = P$

であると仮定します。時刻 $0$ で点 $P$ を通るというわけですね。この関数により定義される曲線を $C_{\phi}$ としましょう。

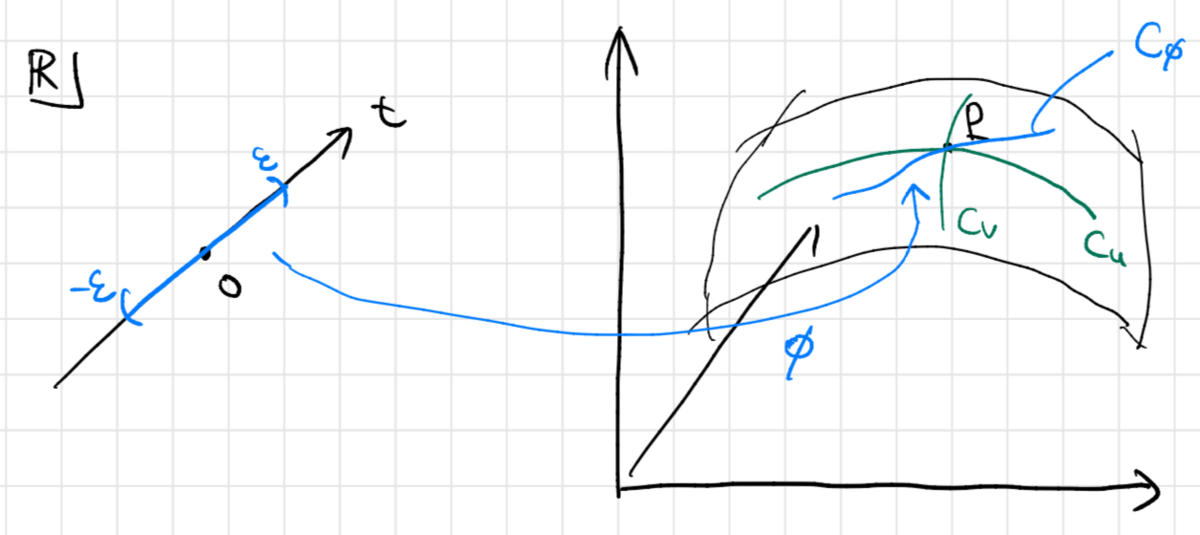
f:id:tsujimotter:20210203093010p:plain:w400

この関数を $t$ で微分して、 $t = 0$ を代入すれば、点 $P$ で $C_{\phi}$ に接する方向ベクトルが得られることになります。

微分を計算すると

$\displaystyle \left.\frac{d}{dt} \phi(t) \right|_{t=0} = \frac{\partial p}{\partial u}(P) \cdot \frac{du}{dt}(0) + \frac{\partial p}{\partial v}(P) \cdot \frac{dv}{dt}(0) \tag{3}$

となります。右辺は、 $\phi(t) = p(u(t), v(t))$ だと思って、2変数の連鎖律（チェーン・ルール）を使って計算していますね。

左辺を $v_{\phi}(p) = \left.\frac{d}{dt} \phi(t) \right|_{t=0}$ と定義しておくと、これは $C_\phi$ に沿った方向ベクトルということになります。

さて、ここで式 $(3)$ の右辺をよく観察すると、 $\frac{du}{dt}(0), \; \frac{dv}{dt}(0)$ は実数値を取りますので、これは $\frac{\partial p}{\partial u}(P)$ と $\frac{\partial p}{\partial v}(P)$ の線形結合になっていることがわかります。

また、 $\phi$ を任意に取り替えても、同様に $C_{\phi}$ に沿った方向微分は $\frac{\partial p}{\partial u}(P)$ と $\frac{\partial p}{\partial v}(P)$ の線形結合で表せます。

したがって、点 $P$ の方向微分全体を表す2次元平面は、 $\frac{\partial p}{\partial u}(P)$ と $\frac{\partial p}{\partial v}(P)$ を基底とするベクトル空間であることが分かります。これを点 $P$ における $S$ の接平面とおくことにしましょう。これを $T_{P}(S)^{?}$ とおくと

$\displaystyle T_{P}(S)^{?} = \left\langle \frac{\partial p}{\partial u}(P), \frac{\partial p}{\partial v}(P) \right\rangle$

ということになります。

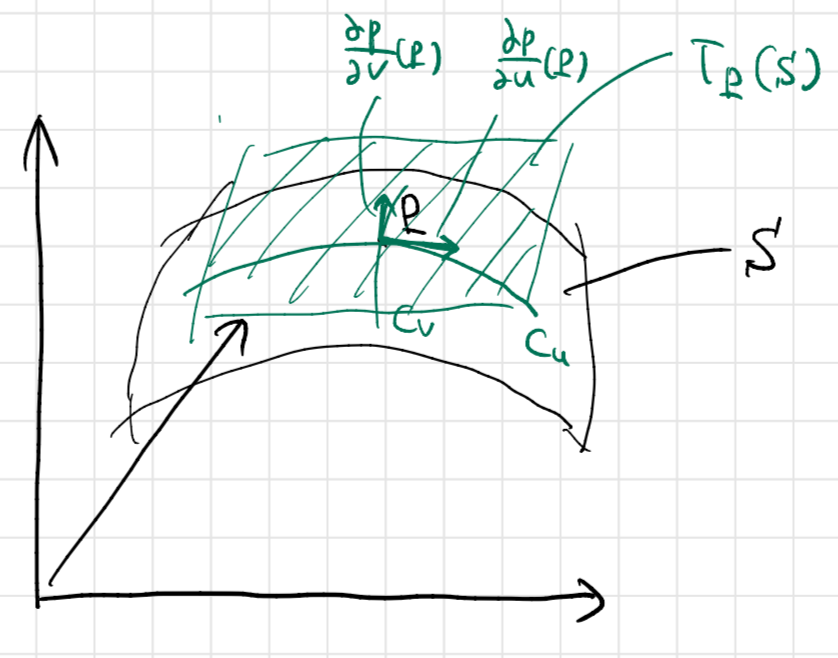
f:id:tsujimotter:20210203093112p:plain:w320

接ベクトル空間に向けた抽象化

現在の接平面 $T_{P}(S)^{?}$ は $p(u, v)$ という、 $\mathbb{R}^3$ 内の曲面 $S$ を定義する関数が明示的に入った形になっています。多様体を考えるにあたっては、 $\mathbb{R}^3$ のような「入れ物の箱」を考えることはありませんので、このような関数は定義からは捨て去りたいという思いがあるのかなと思っています。この辺の痕跡を消しておくことによって一般化がしやすくなるわけですね。

f:id:tsujimotter:20210203093153p:plain:w400

もう一工夫しましょう。

まず、上の $p$ は、実際には $x, y, z$ の3つの関数の組として定義されているのでした。したがって、式 $(3)$ は3つの式

$\displaystyle \left.\frac{d}{dt} x(u(t), v(t)) \right|_{t=0} = \frac{\partial x}{\partial u}(P) \cdot \frac{du}{dt}(0) + \frac{\partial x}{\partial v}(P) \cdot \frac{dv}{dt}(0)$

$\displaystyle \left.\frac{d}{dt} y(u(t), v(t)) \right|_{t=0} = \frac{\partial y}{\partial u}(P) \cdot \frac{du}{dt}(0) + \frac{\partial y}{\partial v}(P) \cdot \frac{dv}{dt}(0)$

$\displaystyle \left.\frac{d}{dt} z(u(t), v(t)) \right|_{t=0} = \frac{\partial z}{\partial u}(P) \cdot \frac{du}{dt}(0) + \frac{\partial z}{\partial v}(P) \cdot \frac{dv}{dt}(0)$

で構成されています。

ここで、左辺では座標として $x(u, v)$ すなわち $\mathbb{R}^2$ から $\mathbb{R}$ への関数を採用していますが、これを使うのをやめます。曲面 $S$ 上の点 $P$ に対して、その $\mathbb{R}^3$ 内の座標を取り出す関数 $\tilde{x} \colon S \to \mathbb{R}$ を使うことにしましょう。すると

$x(u(t), v(t)) = \tilde{x}\circ \phi(t)$

とかけます。右側の関数は合成関数

$(-\varepsilon, \varepsilon) \xrightarrow{\phi} S \xrightarrow{\tilde{x}} \mathbb{R}$

となっていて、入れ物の $\mathbb{R}^3$ やパラメータが明示的に現れない関数となっています。

また、偏微分 $\frac{\partial x}{\partial u}(P)$ についても、 $\frac{\partial \tilde{x}}{\partial u}(P)$ に置き換えます。これについては、 $\tilde{x} \colon S \to \mathbb{R}$ のパラメータ $u, v$ についての表示 $x(u, v)$ を点 $P = p(a, b)$ で偏微分するという意味です。

このようにすると

$\displaystyle \left.\frac{d}{dt} \tilde{x}\circ \phi(t) \right|_{t=0} = \frac{\partial \tilde{x}}{\partial u}(P) \cdot \frac{du}{dt}(0) + \frac{\partial \tilde{x}}{\partial v}(P) \cdot \frac{dv}{dt}(0)$

と書き直せます。同様に、 $\tilde{y}, \tilde{z} \colon S \to \mathbb{R}$ を用いて

$\displaystyle \left.\frac{d}{dt} \tilde{y}\circ \phi(t) \right|_{t=0} = \frac{\partial \tilde{y}}{\partial u}(P) \cdot \frac{du}{dt}(0) + \frac{\partial \tilde{y}}{\partial v}(P) \cdot \frac{dv}{dt}(0)$

$\displaystyle \left.\frac{d}{dt} \tilde{z}\circ \phi(t) \right|_{t=0} = \frac{\partial \tilde{z}}{\partial u}(P) \cdot \frac{du}{dt}(0) + \frac{\partial \tilde{z}}{\partial v}(P) \cdot \frac{dv}{dt}(0)$

ここで、一般に $S$ 上の $C^\infty$ 級関数 $f\colon S \to \mathbb{R}$ を考えて

$\displaystyle \left.\frac{d}{dt} f\circ \phi(t) \right|_{t=0} = \frac{\partial f}{\partial u}(P) \cdot \frac{du}{dt}(0) + \frac{\partial f}{\partial v}(P) \cdot \frac{dv}{dt}(0)$

とした上で、 $f$ に $\tilde{x}, \tilde{y}, \tilde{z}$ をそれぞれ代入しても同じ式が得られますよね。

左辺を $v_{\phi}(f)$ とおきます。 $S$ 上の $C^\infty$ 級関数全体の集合を $\mathcal{A}_{S}$ とおいたときに、 $v_{\phi}$ は $\mathcal{A}_{S}$ の任意の元 $f$ に対して $v_{\phi}(f) = \left.\frac{d}{dt} f\circ \phi(t) \right|_{t=0} \in \mathbb{R}$ を与える関数だと思うことができます。

もはや、 $f$ はとっぱらってしまって、 $v_{\phi}$ 自体を $C_{\phi}$ に沿った方向微分と定義することにしましょう。方向ベクトルの $x$ 成分を具体的に求めたければ、 $v_{\phi}(\tilde{x})$ とすればよいのです。 $(v_{\phi}(\tilde{x}), v_{\phi}(\tilde{y}), v_{\phi}(\tilde{z}))$ を3つ並べたものが方向ベクトルになるわけですね。

J.Koizumiさんという方から「接ベクトルとは座標を与えるごとにその微分を返すものである」というお気持ちを教えていただきましたが、まさにそのような概念であるわけですね。

再度 $v_{\phi}(f)$ の式を与えると

$\displaystyle \begin{align} v_{\phi}(f) &= \frac{du}{dt}(0) \cdot \left(\frac{\partial f}{\partial u}\right)_{P} + \frac{dv}{dt}(0) \cdot \left( \frac{\partial f}{\partial v} \right)_{P} \\ &= \left( \frac{du}{dt}(0) \cdot \left(\frac{\partial }{\partial u}\right)_{P} + \frac{dv}{dt}(0) \cdot \left( \frac{\partial }{\partial v} \right)_{P} \right)(f) \end{align}$

と表すことができますが、両辺ともに $f$ に作用する形で表現されていますので、抽象的な作用素として

$\displaystyle v_{\phi} = \frac{du}{dt}(0) \cdot \left(\frac{\partial }{\partial u}\right)_{P} + \frac{dv}{dt}(0) \cdot \left( \frac{\partial }{\partial v} \right)_{P} \tag{4}$

と定義することができます。ここで

$\displaystyle \left(\frac{\partial}{\partial u}\right)_{P} (f) := \frac{\partial f}{\partial u}(P)$

$\displaystyle \left(\frac{\partial}{\partial v}\right)_{P} (f) := \frac{\partial f}{\partial v}(P)$

となるように $\left(\frac{\partial}{\partial u}\right)_{P}, \left(\frac{\partial}{\partial v}\right)_{P}$ を定義しています。

こんな風に抽象的な作用素になっても、やはり方向微分 $v_{\phi}$ は $\left(\frac{\partial}{\partial u}\right)_{P}, \left(\frac{\partial}{\partial v}\right)_{P}$ の線形結合として表されていますね。

そこで、点 $P$ における方向微分全体の空間を $T_{P}(S)$ と定義すると、 $T_{P}(S)$ は2次元のベクトル空間であり

$\displaystyle T_{P}(S) = \left\langle \left(\frac{\partial}{\partial u}\right)_{P}, \left(\frac{\partial}{\partial v}\right)_{P} \right\rangle$

これを改めて接ベクトル空間と呼べば、多様体の接ベクトルの定義とかなり近いものになるかと思います。

微分作用素

実は多様体的な接ベクトルの定義を模倣して考えると、もう少しだけ抽象化をする必要があります。せっかくなので、軽くその点に触れて終わりにしましょう。

先ほどは、 $v_{\phi}$ という作用素を方向ベクトルの定義としました。これは $v_{\phi} \colon \mathcal{A}_S \to \mathbb{R}$ という関数であったのでした。この関数の持つ性質として、次の２つのものがあります：

（線形性）　 $a, b \in \mathbb{R}, \; f, g \in \mathcal{A}_S$ に対して $v_{\phi}(af + bg) = a v_{\phi}(f) + b v_{\phi}(g)$
（ライプニッツ則）　 $f, g \in \mathcal{A}_S$ に対して $v_{\phi}(f g) = f(P) v_{\phi}(g) + v_{\phi}(f) g(P)$

方向ベクトルは上記の２つの性質を持っているというわけですね。

ここからが発想の飛躍なのですが、逆に上の２つの性質を持つような関数 $v \colon \mathcal{A}_S \to \mathbb{R}$ を接ベクトルの定義としてしまうのです。

正確には、上の２つの性質を満たす関数全体のなすベクトル空間を $D_P(S)$ と表し、 $D_P(S)$ の部分空間であって $\left\langle \left(\frac{\partial}{\partial u}\right)_{P}, \left(\frac{\partial}{\partial v}\right)_{P} \right\rangle$ の生成するものを $T_P(S)$ と表して、その元を接ベクトルというようです。
（今回は $C^\infty$ しか扱っていないので、 $D_P(S) = T_P(S)$ になります。）