クロネッカー・ウェーバーの定理と証明のあらすじ（その３）：クンマー・ペアリング

今日は「クンマー・ペアリング」についてのお話です。

以下のシリーズの続きです。
tsujimotter.hatenablog.com

この記事は，現代数学で尾崎学先生が連載されている「ガロア理論からみた現代数学」で紹介された内容を参考に書いています。該当回は2015年の６月から８月あたりです。

連載の中で紹介された証明は，Neumann による証明をベースにしているそうです。非常に面白いトピックを扱った連載なので，詳しい内容を知りたい方はぜひ購入して読んでみてください。

現代数学 2015年 06 月号 [雑誌]

現代数学 2015年 07 月号 [雑誌]

前回の復習をしましょう。

まず，クンマー拡大とは「１の乗根を十分にもった体 上のべき根拡大」のことです。 上の拡大のガロア群が巡回群であれば（これを巡回拡大という），その拡大の添加元はべき根でかける，ということを示しました。すなわち，巡回拡大はクンマー拡大です。

一般に，ある拡大の添加元から対応するガロア群を得ることは比較的簡単です。一方で，一般のガロア群が与えられたときに，対応する拡大の添加元を得ることは難しい問題です。ところが，巡回拡大に限定してしまえばそれが出来てしまう，というのが面白ポイントです。

前回の命題を再掲しましょう。

命題 2.2（再掲）

を 次の巡回拡大とする．

(1) はアーベル拡大であり， は 次（）の巡回拡大である．

(2) をみたす が存在する．

今回もこの状況を引き継いでお話ししていきます。 として， とします。

さて，前回は上の方のクンマー拡大 におけるガロア群を考えました。下の方の におけるガロア群の作用はどうなるでしょうか，というのが今日のテーマです。

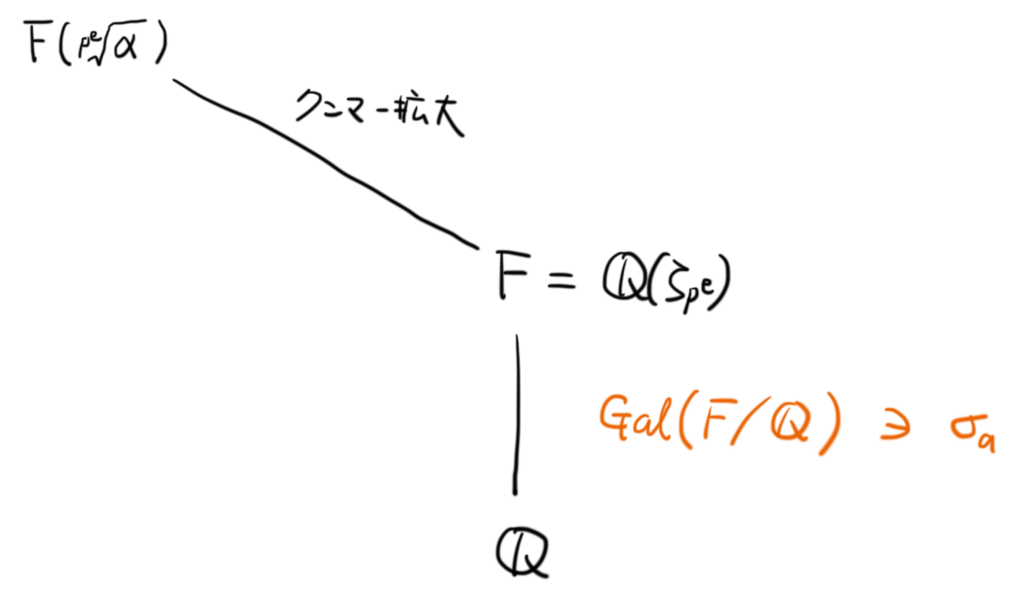
今日の結論を先に言ってしまうと「クンマー・ペアリング」という方法を使って，以下のように決定できます。

命題 3.1

命題 2.2 の条件下で， としたとき，以下が成り立つ：

ただし， は で定まる自己同型写像である．

命題のイメージが湧きにくいかもしれない（私もわからなかった）ので補足をします。

この命題は， という元に を作用させたとき，どのような元に移り変わるかを与えるものです。ざっくり言うと， に を作用させると， が「ほぼ 乗される」のです。「ほぼ 乗される」ということの意味は， に「定数倍」だけかけた分のズレがあるということです。その定数は の 0 でない元を 乗したものになります。言い換えると， に対して の元 が存在して

が成り立ちます。 倍を無視すれば， 乗という形のわかりやすい形で の作用がかけるというわけですね。

この関係って何かに似ていませんか。ほら，

こういう式です。先ほどの式の「積」の箇所をすべて「和」に置き換えてみました。このとき，

と書きますね。つまり合同式と同じ式です。 の分を無視すれば等号が成り立つということです。

さて，命題の主張の説明はこの辺にしておきましょう。証明に移りたいところですが，いくつか道具の準備が必要です。一通り道具を準備した上で，最後に証明することにしましょう。

クンマー・ペアリング

まず今回の記事を通して， は の原始 乗根全体 を含む標数 0 の体 とします。

前回示したように，任意の 次の巡回拡大 には， が存在して と表せるクンマー拡大となっています。以下，クンマー拡大 のガロア群を考えましょう。

ガロア群 の元 を考えたとき， の への作用は，１の 乗根 を用いて

と表せます。なぜなら， という量を考えて，これを 乗すると

となり， が１の 乗根とわかるからです。

また， に の 乗数 を掛けて得られる集合 を考えます。 をべき乗していくと，

が得られますが， は の元ですから，

です。したがって は 次の巡回群をなします。

この巡回群の構造ですが，

となっています（右辺は 0 でない の元で 乗数の因子を無視したもの，左辺は から 乗数の因子を無視したもの）。さらにいうと，

が成り立つことが示せます。 は 乗して の元になる 0 でない の元です。

また， に対して，

が成り立ちます。

この巡回群の元 を考えて， に対して同様の量 を考えると，これに対しても，

が成り立ちます。証明の方法はまったく同様です（両辺を 乗する）。

この という量は として のどの代表元をとっても，同じ値となることに注意しましょう。つまり， は と の組に対して一意に定まります（Well-defined）。

以上の点を踏まえて，次のような写像を考えることが自然に思えます。

定義：クンマー・ペアリング

以下で定義される２変数関数 をクンマー・ペアリングという．

「ペアリング」というのは，双線型性をもった２変数関数のことです*1。順を追って説明していきます。

まず，変数の片方を固定したとき，それぞれ写像になっていることに注意してください。
を固定したとき，

は， から への写像となっています。 の写像を と書くことにしましょう。

逆に を固定したとき，

は， から への写像となっています。 の写像を と書くことにしましょう。

さて双線型性とは，これら２つの写像が次のような「線型性」を持っているということです。

命題 3.2：クンマー・ペアリングの双線型性

と に対して次が成り立つ：

と に対して次が成り立つ：

以上の式の証明は簡単です。

（証明）

まずは式 から示す．

次に式 を示す．

■

以上から， と はそれぞれ準同型写像であることがわかるので， と であることがわかります *2。

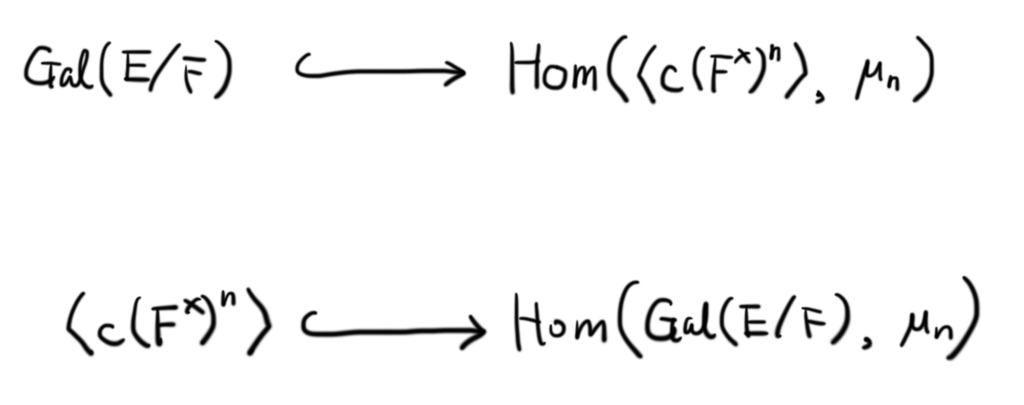
さて， に対して， という写像が定まります。したがって，

という対応が存在するわけですが，これが同型写像になっている，というのが次の「完全性」という性質です。

命題 3.3：クンマー・ペアリングの完全性

この完全性が命題 3.1 の証明のキーとなります。群準同型 が全単射というのが命題 3.3 の主張ですが，これによって という等式を示すことができれば， という等式が導けるのです。

証明も面白いです。式 と式 を同時に示すことになります。

（証明）
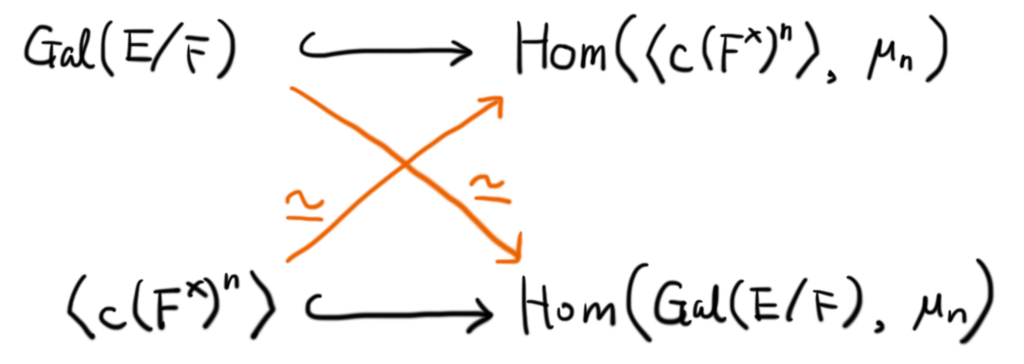
まず単射準同型を示す（省略）．

次に，位数 の約数である有限群 に対して

が成り立つ．したがって，

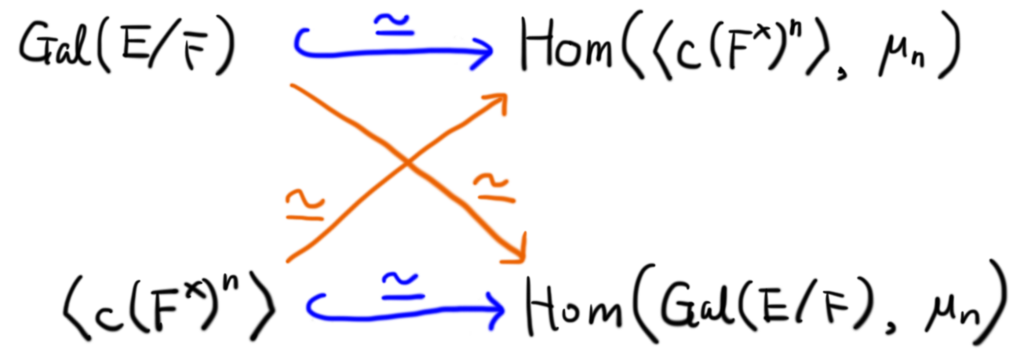
が得られる．これで，以下の図式がクロスに同型になる．

単射性と合わせてすべての位数が一致することがわかり，同型が得られる．

■

次に，クンマー拡大 の下に なる部分体があるケースを考えましょう。最終的には のケースを考えたいのですが，ここでは一般に としておきます。

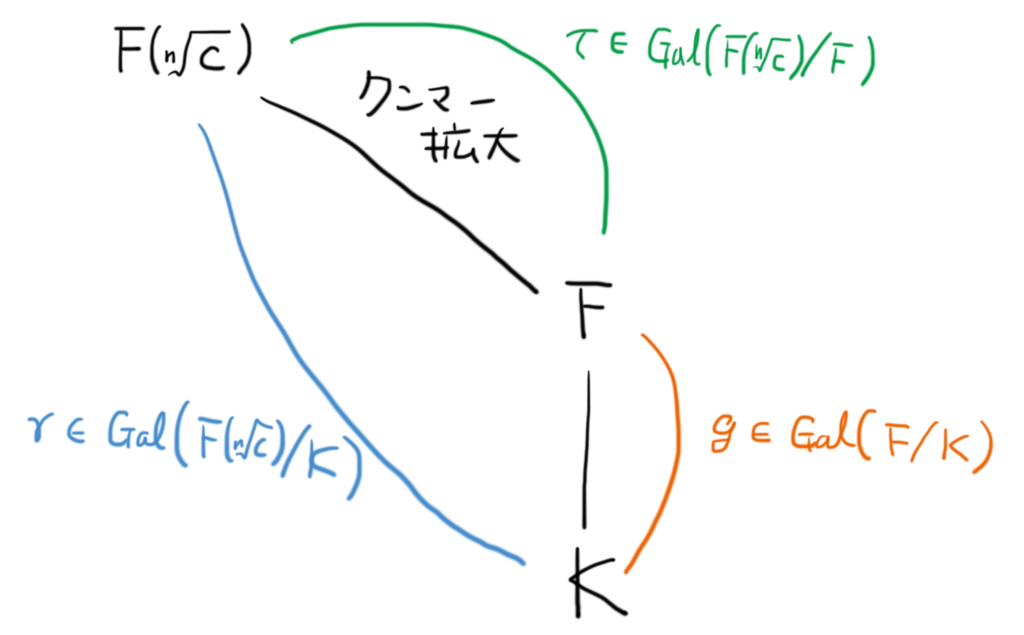
このとき，今度は のガロア群を考えます。すると，以下が成り立ちます．

命題 3.4（前半）

の部分体 と について， と が有限次ガロア拡大であると仮定する．

このとき， は， の作用で閉じている．つまり，任意の に対して，

が成立する．

証明は以下の通りです。

（証明）
任意の に対して， となる が存在する．
（「 は本来 の自己同型写像ですが，これを に制限すると と一致する」そんな が存在すると言っています）

このとき， は の自己同型写像より， である．したがって， 乗した は の元である．また， は の自己同型写像より である．

一方， は の元であるから， である．よって， は の元かつ の元であるから，

である． での同値類をとると

となり，式 から

である．

■

命題 3.4（後半）

クンマー・ペアリングにおいて，任意の に対して，

が成立する．

は大きな拡大のガロア群の元， は上のクンマー拡大のガロア群の元であることに注意します。

（証明）
クンマー・ペアリングの定義より，

であるが， である（両辺を 乗することでわかります）．

よって， に注意し，

が言える．

■

命題 3.1の証明

それでは，ようやく準備が整いましたので，命題 3.1を示しましょう。

命題 3.1を再掲します。

命題 3.1（再掲）

命題 2.2 の条件下で， としたとき，以下が成り立つ：

ただし， は で定まる自己同型写像である．

命題 2.2 のセッティングを確認しておきましょう。

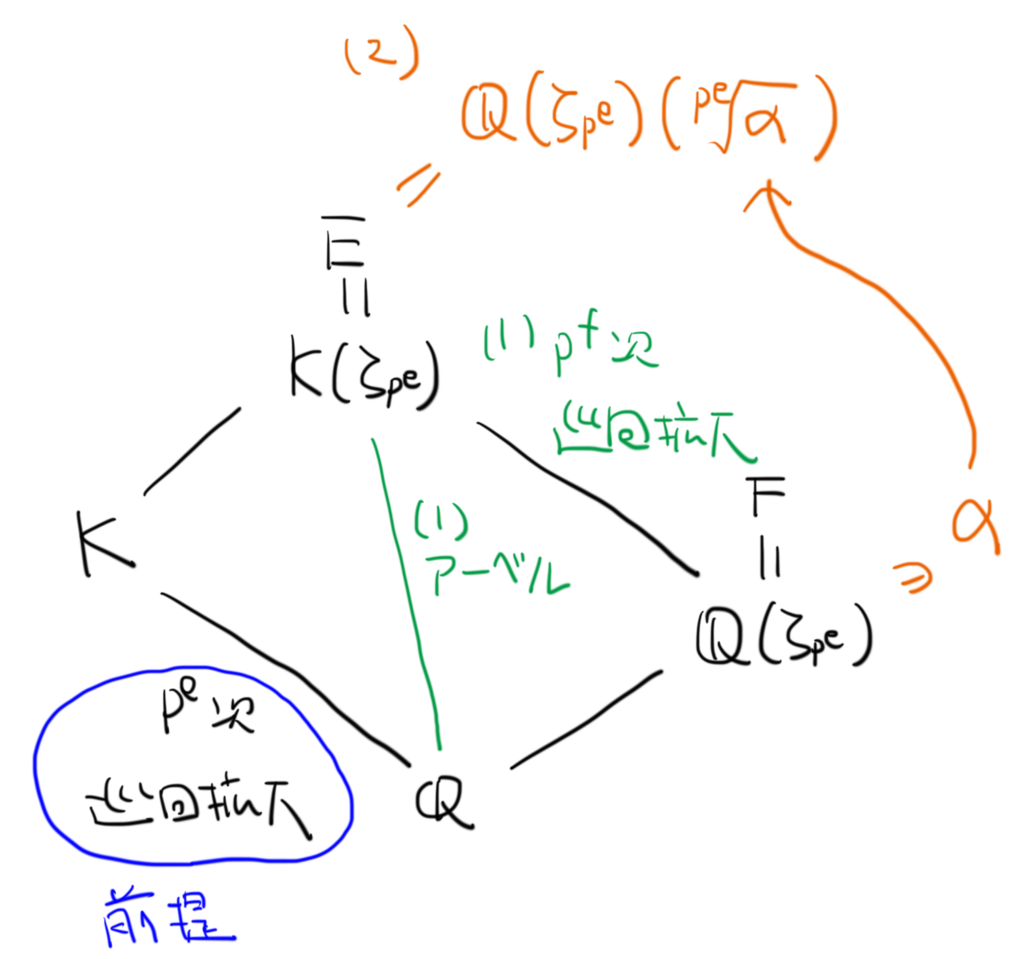
とおくと， はクンマー拡大となっています。さらに， ですから として命題 3.4 の条件が適用できます。加えて， は円分拡大となっていて，そのガロア群の元 は，

と表せることに注意します。

（証明）
を なる元とする．

はアーベル群であるから，任意の に対して

が成り立つ．

また，命題 3.4（前半）の主張より， であるから，クンマー・ペアリング を考えることができる．

よって，任意の に対して

となり，

が得られた．

ここで，命題 3.3（クンマー・ペアリングの完全性）の式 より， ならば であるから，

が得られる．

■

まとめと次回予告

やっと終わりました。だいぶ長かったので簡単にまとめましょう。

まず，今回証明したかったのは， としたときに，

が成り立つというものでした。このままだと難しいので，いったん をクンマー・ペアリング に入れ込みます。

クンマー・ペアリングの性質（命題3.2, 3.3, 3.4）によって，見事

を示すことができ，クンマー・ペアリングの完全性によって，求める等式が得られたという流れです。

①一旦ペアリングに入れ込んで
②ペアリングの性質をつかって変形し
③戻す

という問題解決の方法が，なかなか面白いなと思いました。

さて，今回 の に対する作用の様子がわかったわけですが，次回はこの情報を使っていきます。具体的には を組み合わせて作った Stickelberger元 という特別な元を考えて，これによって を表す方法を考えます。

このStickelberger元ってやつが面白くって，任意の 上のイデアルに作用させると単項イデアルになって，しかもその生成元が「ガウス和」で表せるのだそうです！なにそれ超面白そう！

それでは今日はこの辺で。

（このシリーズ，いったいいつ終わることやら・・・）

*1:"pair ring" ではないことに注意。正しくは "pairing" です。

*2: は から への準同型写像全体の集合のこと