クロネッカー・ウェーバーの定理と証明のあらすじ（その２）：クンマー拡大

ご無沙汰しています。tsujimotterです。

久しぶりに「クロネッカー・ウェーバーの定理と証明のあらすじ」シリーズの続きを書きたいと思います。
tsujimotter.hatenablog.com

今日の主役はクンマー拡大です。クンマー拡大とは，「巡回拡大」が「ベキ根の添加」によってかけるような拡大のことです。このような拡大のときは，いろいろと都合がよい性質があるのです。

この記事は，現代数学で尾崎学先生が連載されている「ガロア理論からみた現代数学」で紹介された内容を参考に書いています。該当回は2015年の６月から８月あたりです。

連載の中で紹介された証明は，Neumann による証明をベースにしているそうです。非常に面白いトピックを扱った連載なので，詳しい内容を知りたい方はぜひ購入して読んでみてください。

現代数学 2015年 06 月号 [雑誌]

出版社/メーカー: 現代数学社
発売日: 2015/05/12
メディア: 雑誌
この商品を含むブログを見る

現代数学 2015年 07 月号 [雑誌]

出版社/メーカー: 現代数学社
発売日: 2015/06/12
メディア: 雑誌
この商品を含むブログを見る

クンマー拡大の定義

まず，クンマー拡大を定義することから始めましょう。

この記事全体の前提として， $F$ は標数 0 の体で 1 の $n$ 乗根全体 $\mu_n$ を含むとします。

「標数」という言葉は，tsujimotterのノートブックでは初めて登場しましたね。体の標数は，体の単位元 1 を何回足すと 0 になるかを表す整数として定義されます。位数 $p^e$ の有限体は， $1$ を $p$ 回足すと $0$ になりますね。代数体では， $1$ を何回足しても $0$ になりません。この場合は，標数は $0$ とします。

今回の場合は， $F$ を代数体に限定して構いません。さらに， $F$ は 1 の $n$ 乗根全体を含むので，たとえば， $F = \mathbb{Q}(\zeta_{n})$ を想像してください。

命題 2.1：クンマー拡大

任意の $n$ 次巡回拡大 $E/F$ に対して， $E = F(\sqrt[n]{c})$ なる $c \in F^\times$ が存在する．

また， $F$ が $\mu_n$ を含むとき，拡大 $F(\sqrt[n]{c})$ を クンマー拡大 という．

状況としては，こんな状況を想像してもらえればと思います。

f:id:tsujimotter:20171029212805p:plain:w400

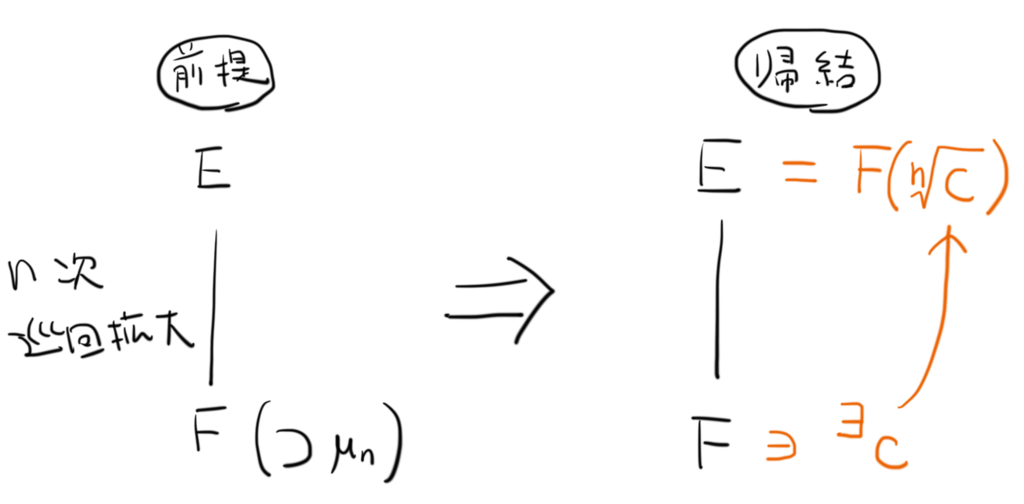
巡回拡大 $E/F$ があるときに，基礎体 $F$ に $c$ の $n$ 乗根を添加すると $E$ に一致するような「都合の良い $c$ 」が存在するという主張です。

これから証明について述べていきますが，本記事では $n$ は素数のべき，すなわち， $n = p^e$ （ $p$ は素数， $e$ は正整数）に限定して考えたいと思います。クンマー拡大の命題は一般の $n$ について成り立つものですが，このシリーズで必要なのは $n = p^e$ の場合だけです。

証明は以下のような流れで進めます。

前提である「 $1$ の $p^e$ 乗根」と「巡回置換」を用いて， $\sqrt[p^e]{c}$ の候補となる複数の元 $\xi_0, \xi_1, \xi_2, \cdots, \xi_i, \cdots, \xi_{p^e - 1} \in E$ を作る。
上の候補の中から $\xi_{i_0} \neq 0$ となる $i_0$ が存在することを示す。
$E = F(\xi_{i_0})$ であることを示す。
$\xi_{i_0}^{p^e}$ は，実は $F$ の元であることがわかるので，これを $c = \xi_{i_0}^{p^e}$ とする。

まず，証明の舞台となるセッティングについて述べていきましょう。

$E/F$ は $p^e$ 次巡回拡大なので， $\mathrm{Gal}(E/F) = \langle \sigma\rangle \simeq \mathbb{Z}/p^e \mathbb{Z}$ と書くことができます。また， $E = F(\eta)$ となるような $\eta \in E$ をとりましょう（ $F$ にある特定の元を添加したら $E$ になるはずなので，そのような元をひとまず $\eta$ としておくのです）。さらに， $1$ の原始 $p^e$ 乗根の１つを $\zeta_{p^e} \in F^\times$ としておきましょう。

以下のような状況です。

f:id:tsujimotter:20171030205315p:plain:w360

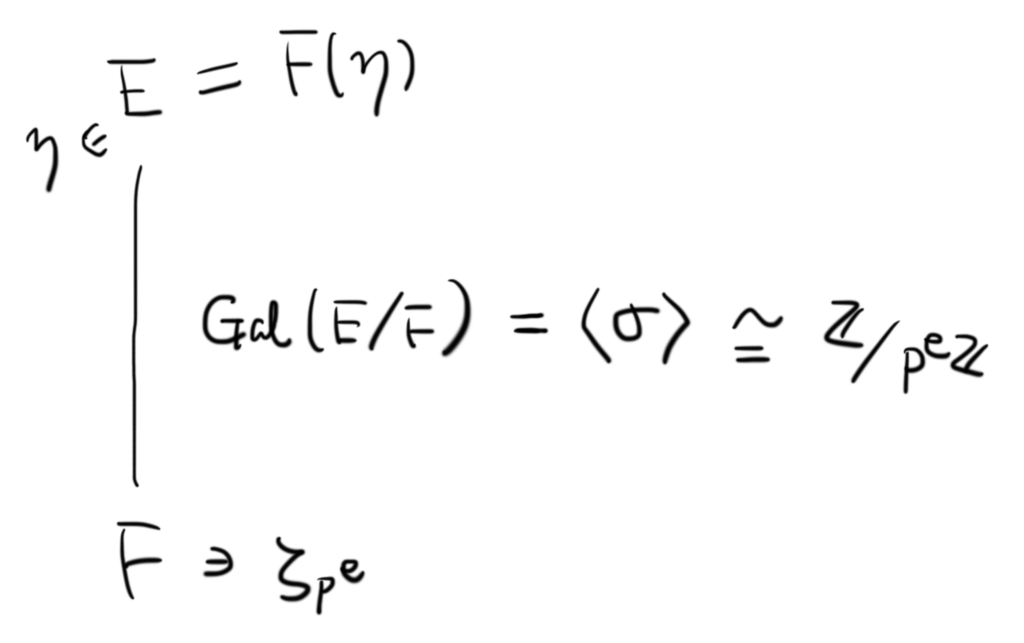
さて，証明に取り掛かります。

（証明）

まず， $0 \leqq i \leqq p^e - 1$ に対して，以下の式で定義される元 $\xi_i$ を考えます。

$\displaystyle \xi_i := \sum_{k=0}^{p^e - 1} \zeta_{p^e}^{ik} \sigma^k(\eta)$

以上の元に $\sigma$ を作用させると

$\sigma(\xi_i) = \zeta_{p^e}^{-i} \xi_i \tag{1}$

が成立します。

これから， $\xi_0, \cdots , \xi_i, \cdots, \xi_{p^e - 1}, \;\; \mathrm{gcd}(p, i) = 1$ なる $i$ の中で，少なくとも１つは $\xi_{i} \neq 0$ であるものが存在することを示します。

ここで，すべての $0 \leqq i \leqq p^e - 1, \;\; \mathrm{gcd}(p, i) = 1$ に対して， $\xi_i = 0$ と仮定すると，

$\displaystyle \sum_{j=0}^{p^{e-1} - 1} \xi_{pj} = \sum_{i=0}^{p^e - 1} \xi_{i}$

が成り立つ。

この等式を「ぱっと」イメージできる人は，この手の議論に十分慣れている人だと思います。私はわからなかったので，具体的に計算します。

以下の図は $p = 5, e = 2$ の例です。
f:id:tsujimotter:20171029221824p:plain:w400

さらに， $\xi_i$ の定義式を展開すると

$\displaystyle \sum_{j=0}^{p^{e-1} - 1} \xi_{pj} = \sum_{i=0}^{p^e - 1} \xi_{i} = \sum_{k=0}^{p^e - 1} \left( \sum_{i=0}^{p^e - 1} \zeta_{p^e}^{ik} \right)\sigma^k(\eta)$

ここで，

$\displaystyle \sum_{i=0}^{p^e - 1} \zeta_{p^e}^{ik} = \begin{cases} p^e & (k=0) \\ 0 & (k\neq 0) \end{cases}$

より，

$\displaystyle \sum_{j=0}^{p^{e-1} - 1} \xi_{pj} = \sum_{i=0}^{p^e - 1} \xi_{i} = \sum_{k=0}^{p^e - 1} \left( \sum_{i=0}^{p^e - 1} \zeta_{p^e}^{ik} \right)\sigma^k(\eta) = p^e \eta \tag{2}$

が成り立つ。

式 $(1)$ より，

$\displaystyle \sigma^{p^{e-1}} \left( \sum_{j=0}^{p^{e-1} - 1} \xi_{pj} \right) = \sum_{j=0}^{p^{e-1} - 1} \xi_{pj}$

すなわち， $\sigma^{p^{e-1}}$ の作用に対して不変であるので， $(2)$ より

$\displaystyle \sigma^{p^{e-1}} \left( p^e \eta \right) = p^e \eta$

が結論される。ここで，以下のようなガロア対応を考える。

f:id:tsujimotter:20171029213558p:plain:w300

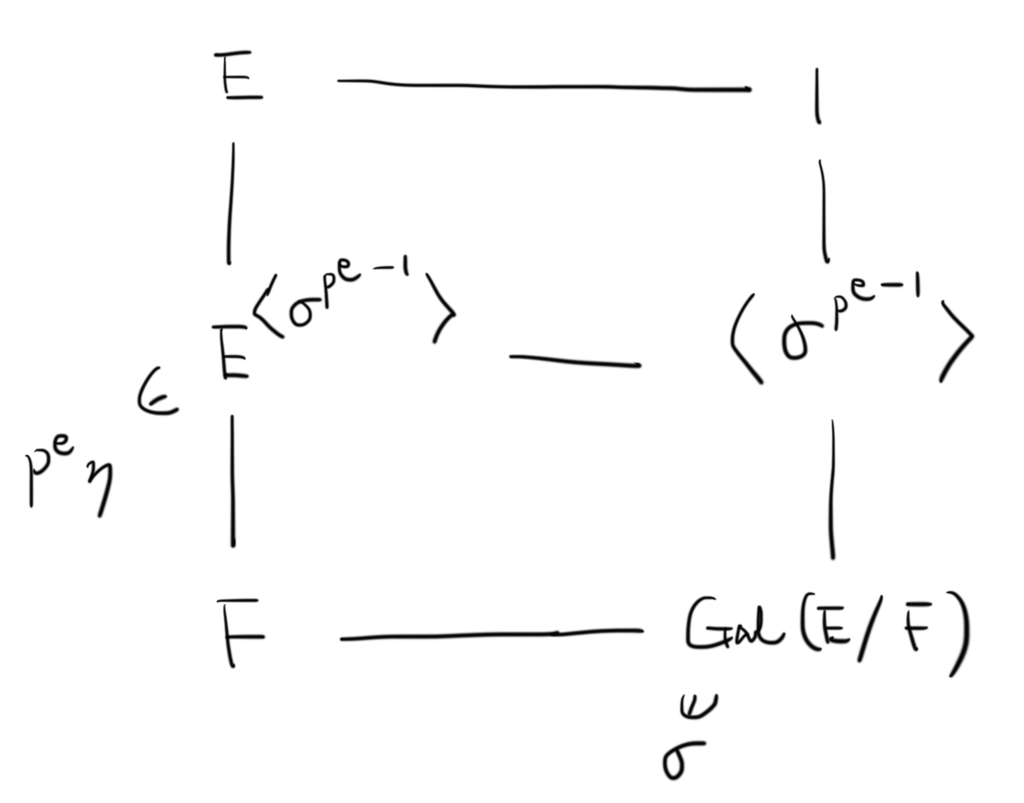
$p^f \eta$ は $\sigma^{p^{e-1}}$ の作用によって不変なので $p^e\eta \in E^{\langle \sigma^{p^{e-1}} \rangle}$ であるが， $\langle \sigma^{p^{e-1}} \rangle \neq 1$ である（ $\sigma^{p^{e-1}}$ が自明であれば $\sigma^{p^{e-1}} = 1$ であるが， $\sigma$ の位数は $p^e$ であるからおかしい）。

したがって，Galoisの基本定理より $p^e\eta \in E^{\langle \sigma^{p^{e-1}} \rangle} \subsetneq E$ である。しかしこれは $E$ の定義，すなわち， $E = F(\eta) = F(p^e \eta)$ に矛盾する。

よって，少なくともある $1 \leqq i_0 \leqq p^e - 1, \;\; \mathrm{gcd}(p, i_0) = 1$ について $\xi_{i_0} \neq 0$ であることが示された。

このとき， $\zeta_{p^e}^{i_0}$ の $\mu_{p^e}$ における位数は $p^e$ なので（ $\zeta \in \mu_{p^e}$ は $p^e$ 乗すると $1$ になる）， $(1)$ から $\sigma^k(\xi_{i_0}) = \xi_{i_0} \Longrightarrow \sigma^k = 1$ がわかる（ $k = p^e$ のときに限り $\sigma^{p^e} = 1$ となり不変）。よって， $\mathrm{Gal}(E/F(\xi_{i_0})) = 1$ なので，Galoisの基本定理から $F(\xi_{i_0}) = E$ となる。

また， $(1)$ から $\sigma(\xi_{i_0}^{p^e}) = \xi_{i_0}^{p^e}$ も出るので，再びGaloisの基本定理から $\xi_{i_0}^{p^e} \in F$ がわかる。よって，

$c = \xi_{i_0}^{p^e} \in F^\times$

が得られ， $E = F(\sqrt[p^e]{c})$ を満たす $c \in F^\times$ を見つけることができた。

■

前回の議論に戻って

さて，ここで前回の $\mathbb{Q}$ 上のアーベル拡大の議論に戻りましょう。

前回は，クロネッカー・ウェーバーの定理の証明を $K/\mathbb{Q}$ が $p^e$ 次の巡回拡大のケースに帰着したのでした。今回は，次のステップとして，この巡回拡大をベキ根を使って表すことにします。

ただし，クンマー拡大はこのままでは使えません。なぜなら， $K/\mathbb{Q}$ の基礎体である $\mathbb{Q}$ は「1 の $p^e$ 乗根すべて」を含まないため，クンマー拡大の条件を満たさないからです。

ではどうするか。ここが一番面白いポイントです。

$K$ と $\mathbb{Q}$ それぞれに，1 の $p^e$ 乗根 $\zeta_{p^e}$ を添加してしまうのです。図で表すと，こういう状況です。

f:id:tsujimotter:20171029214325p:plain:w360

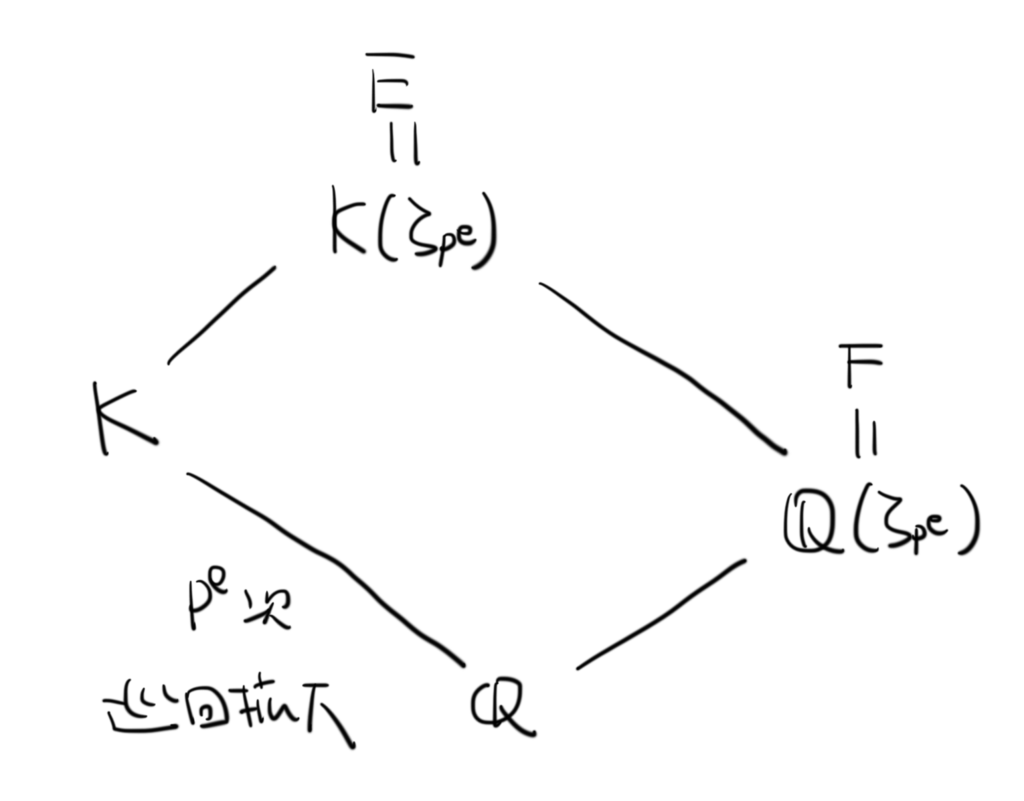
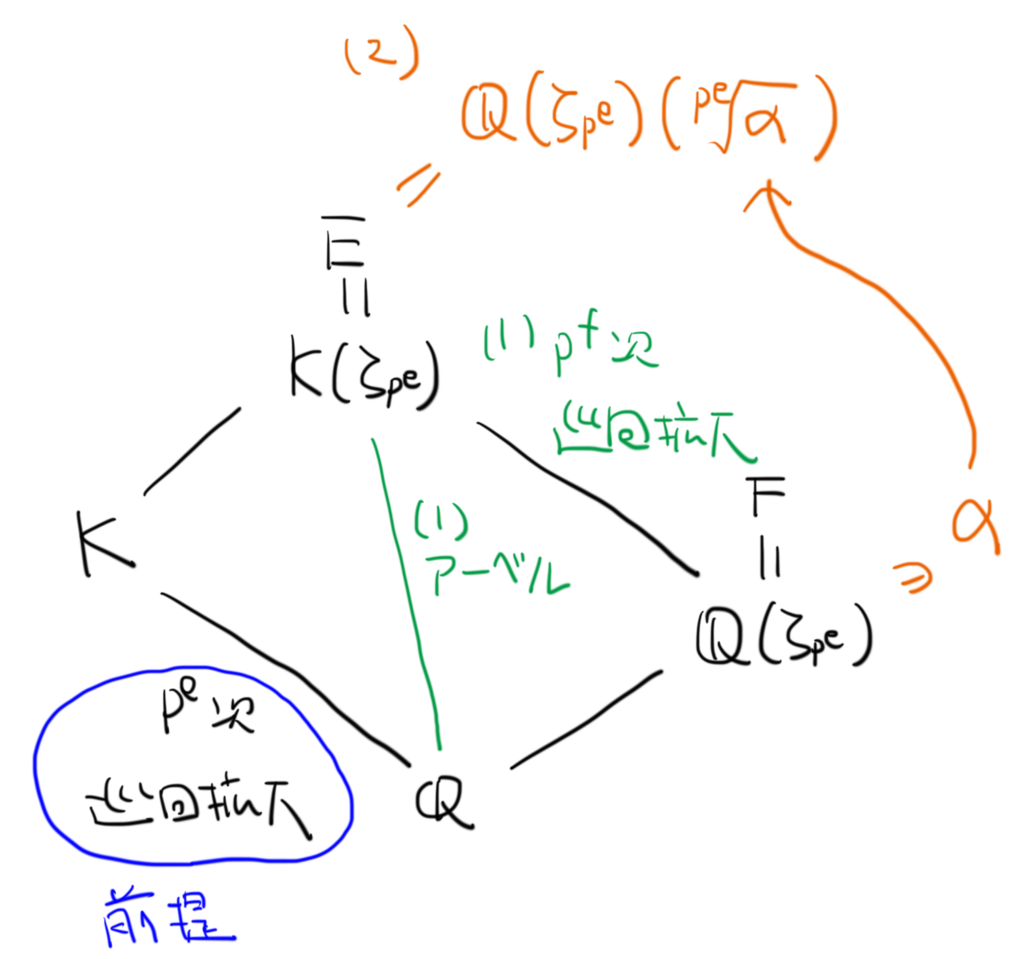
何やらややこしいことをして，これで収拾がつくのだろうかと思うかもしれません。でもこれでうまくいくのです。次のような命題が成り立ちます。

命題 2.2

$K/\mathbb{Q}$ を $p^e$ 次の巡回拡大とする．

(1) $K(\zeta_{p^e})/\mathbb{Q}$ はアーベル拡大であり， $K(\zeta_{p^e})/\mathbb{Q}(\zeta_{p^e})$ は $p^f$ 次（ $f \leqq e$ ）の巡回拡大である。

(2) $K(\zeta_{p^e}) = \mathbb{Q}(\zeta_{p^e})(\sqrt[p^e]{\alpha})$ をみたす $\alpha \in \mathbb{Q}(\zeta_{p^e})^\times$ が存在する。

命題 2 の状況を図に書き加えるとこうなります。

f:id:tsujimotter:20171029214255p:plain:w360

(1) の証明

まず， $K(\zeta_{p^e})/\mathbb{Q}$ がGalois拡大であることが（示しませんが）わかります。

また，

f:id:tsujimotter:20171029215128p:plain:w400

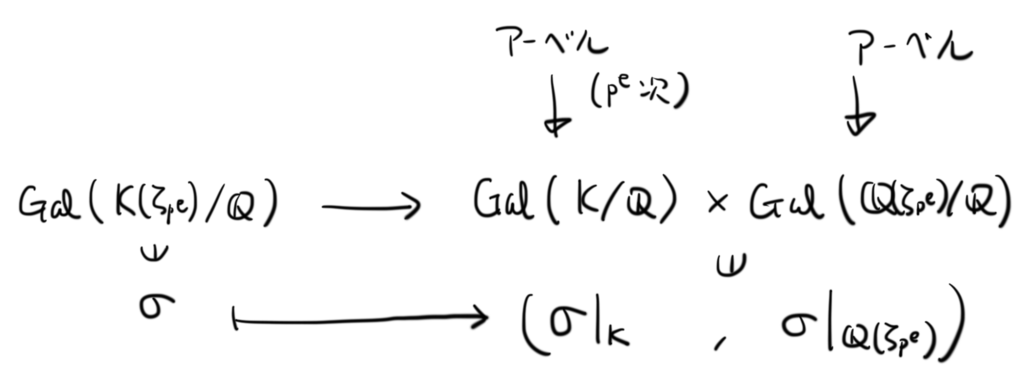
が単射準同型である（右のほうが大きい群で，左の群が埋め込まれる）。右辺の群はアーベル群の直積なので，左辺もアーベル群であることがわかる。よって， $K(\zeta_{p^e})/\mathbb{Q}$ はアーベル拡大（(1) の前半が証明できた）。

さらに，

f:id:tsujimotter:20171029215155p:plain:w380

も単射準同型であることがわかる。右辺の群の位数は $p^e$ 次で，左辺の群はこれを割り切るから， $p^f$ 次（ $f \leqq e$ ）であるという主張も示された。

■

(2) の証明

(1) より， $K(\zeta_{p^e})/\mathbb{Q}(\zeta_{p^e})$ は $p^f$ 次巡回拡大である。また， $\mu_{p^f} \subset \mu_{p^e}$ より $\mathbb{Q}(\zeta_{p^e})$ は 1 の $p^f$ 乗根すべてを含む。

したがって命題 1 より， $K(\zeta_{p^e}) = \mathbb{Q}(\zeta_{p^e})(\sqrt[p^f]{\alpha})$ を満たす $\alpha \in \mathbb{Q}(\zeta_{p^e})^\times$ が存在する。

ここで， $\alpha' := \alpha^{p^e/p^f}$ とすると，

$\sqrt[p^e]{\alpha'} =\sqrt[p^f]{\alpha}$

であり，さらに $\alpha' = \alpha^{p^{e-f}} \in \mathbb{Q}(\zeta_{p^e})^\times$ である。したがって， $K(\zeta_{p^e}) = \mathbb{Q}(\zeta_{p^e})(\sqrt[p^e]{\alpha'})$ をみたす $\alpha' \in \mathbb{Q}(\zeta_{p^e})^\times$ を見つけることができた。

■

まとめと次回予告

以上の議論によって， $\alpha \in \mathbb{Q}(\zeta_{p^e})^\times$ という元が存在して，任意の $p^e$ 次巡回拡大 $K/\mathbb{Q}$ に対して

$\mathbb{Q} \subset K \subset K(\zeta_{p^e}) = \mathbb{Q}(\zeta_{p^e}, \sqrt[p^e]{\alpha})$

という包含関係を示すことができました。あとは，べき根の部分を含む $\mathbb{Q}(\zeta_{p^e}, \sqrt[p^e]{\alpha})$ が， $\mathbb{Q}$ 上の円分拡大に含まれることを示せばオーケーです。

今回 $\alpha = \xi_{i_0}^{p^e}$ という元の存在を示すことに成功しましたが，このような元を実際に構成するのは困難です。というのも， $\xi_{i_0}$ の定義には $\eta \in E$ という未知の元が必要でしたし， $i_0$ も $0 \leqq i_0 \leqq p^e - 1$ で $\mathrm{gcd}(p, i_0) = 1$ かつ $\xi_{i_0} \neq 0$ という条件でした。このような $i_0$ を具体的に見つけるのは困難です。そのため，前回示した二次拡大の場合のような方向性の証明は難しそうです。

我々の目的はクロネッカー・ウェーバーなので， $\alpha \in F^\times$ という元を $\mathbb{Q}$ 上の円分拡大の中で表現できればよいと考えます。そこで， $E/\mathbb{Q}$ のガロア群を考えることになります。 $\alpha \in F^\times$ は，クンマー拡大 $E/F$ のガロア群 $\mathrm{Gal}(E/F)$ に対しては不変となります（ $\sqrt[p^n]{\alpha}$ は $\mathrm{Gal}(E/F)$ に対して分かりやすい振る舞いをします）。