クンマー理論 - tsujimotterのノートブック

クンマー拡大についての記事を準備しているうちに，いくぶん理解が進んできました。
tsujimotter.hatenablog.com

今日は，本題の「クロネッカー・ウェーバーの定理」から離れて「クンマー理論」について紹介します。クンマー理論については，しばらく前からずっと理解したいと思っていたものでしたので，ちょうどよい機会だと思いました。

特に，クンマー理論の主定理の理解を目指しましょう。

クンマー理論のセッティング

まず，１の $n$ 乗根全体の集合を $\mu_n$ とおきましょう。前回同様， $K$ は標数 $0$ の体で， $\mu_n$ を含むとします（ $\mu \subset K$ ）。この $K$ 上の拡大体を考えることにします。

$K^\times$ は $K$ の乗法群といって， $K$ の可逆元全体のなす群を表します。

体なので， $0$ を除けばすべて可逆元ですから（逆数を持つ）， $0$ を除いた $K$ の元のなす掛け算の群と思ってもらえればよいです。

乗法群 $K^\times$ に対して， $K^\times$ の $n$ 乗数全体の集合 $(K^\times)^n$ は $K^\times$ の部分群をなします。

$K^\times$ を部分群 $(K^\times)^n$ で割った剰余群を考えましょう。これがなかなかイメージしづらいのですが，具体的に考えるのが肝心です。 $K^\times$ の元は

$p^{a}q^{b}r^{c}s^{d}\cdots$

と素因数分解できますね。 $K^\times$ は $n$ 乗数全体の群です。 $K^\times$ で割った剰余群においては $n$ 乗の分が同一視されます。したがって， $a', b', c', d', \cdots$ をそれぞれ $a, b, c, d, \cdots$ を $n$ で割ったあまりとして

$p^{a'}q^{b'}r^{c'}s^{d'}\cdots(K^\times)^{n}$

という元が $K^\times/(K^\times)^n$ の元となります。

次に， $(K^\times)^n \subset D \subset K^\times$ なる $D$ という部分群を考えます。 $[ D:(K^\times)^n]$ は有限としておきます。

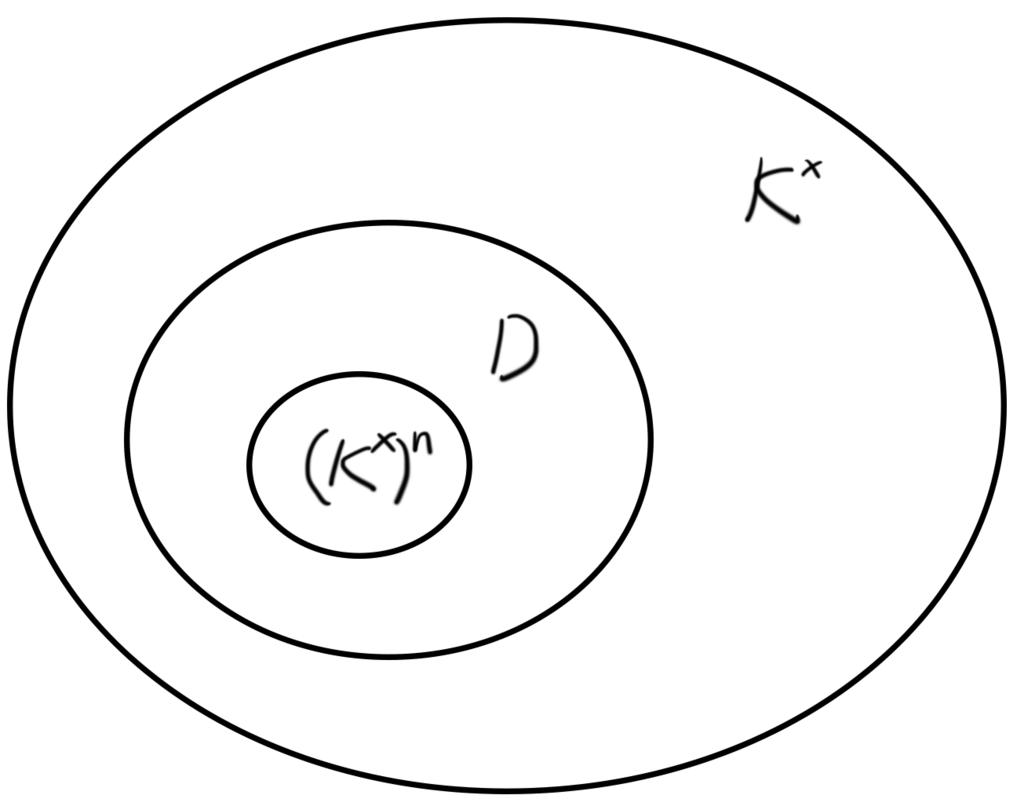
この $D$ も少しイメージしづらいですが，あとで具体例をたくさん出しますので，それで理解してください。

以上の $D$ に対して $\sqrt[n]{D}$ という集合を考えます。これは， $D$ のすべての元に対して $n$ 乗根をとり，それらをそのまま集合としたものです。

$\sqrt[n]{D} = \left\{ \sqrt[n]{a} \; \middle| \; a \in D \right\}$

この $\sqrt[n]{D}$ をすべて添加した $K$ の拡大体を $K(\sqrt[n]{D})$ と表します。 $(K^\times)^n$ の $n$ 乗根については根号が取れて $K^\times$ の元になりますから， $D/(K^\times)^n$ を考えると良いでしょう。 $D/(K^\times)^n$ の完全代表系を $\{a_1, a_2, a_3, \cdots, a_t\}$ とすると，

$K( \sqrt[n]{D} ) = K( \sqrt[n]{a_1}, \sqrt[n]{a_2}, \sqrt[n]{a_3}, \cdots , \sqrt[n]{a_t} )$

と表せます。たくさん「べき根」を添加した体といえるでしょう。これがクンマー拡大です。

定義：クンマー拡大

$K$ を標数 $0$ の体で， $\mu_n$ を含むとする．

$D$ を $(K^\times)^n \subset D \subset K^\times$ で $[ D:(K^\times)^n]$ が有限である任意の部分群としたとき， $K(\sqrt[n]{D})/K$ の形をした拡大を指数 $n$ のクンマー拡大という．

ここから，次節で紹介する「クンマー理論の主定理」を少し先取りして「クンマー理論によってどんなことが言えるのか」について説明しましょう。

「クンマー理論の主定理」により $K( \sqrt[n]{D} )$ は指数 $n$ のアーベル拡大（ガロア群がアーベル群で指数が $n$ である，ということ）となることが言えます。すなわち， $D$ が定まるとそれに呼応して $L = K( \sqrt[n]{D} )$ という指数 $n$ のアーベル拡大が定まります。

注：指数とは，群の任意の元を $n$ 乗（加法群の場合は， $n$ 倍）したときに，単位元になるような最小の $n$ のことです。

群論のフェルマーの小定理より，群 $G$ の任意の元は $\# G$ 乗すると単位元になりますが，位数と指数は一致するとは限りません。
tsujimotter.hatenablog.com

たとえば， $\mathbb{Z}/n\mathbb{Z}$ は指数 $n$ ですが， $\mathbb{Z}/n\mathbb{Z}\oplus \mathbb{Z}/n\mathbb{Z}$ も指数 $n$ です。この場合は，位数は $n^2$ になりますね。

逆に，指数 $n$ のアーベル拡大 $L/K$ があったとすると， $D = (L^\times)^n \cap K$ として $D$ が得られます。

$(L^\times)^n \cap K$ は「 $L$ の $n$ 乗数」かつ「 $K$ の数」であるような数です。

$L$ は $K$ の元を含みますから，上の集合は $K$ の $n$ 乗数を含みます。 $K$ の $n$ 乗数以外で， $n$ 乗して $K$ になる $L$ の数は， $L = K( \sqrt[n]{D} )$ としたときの $D$ に含まれる数だけです。

よって， $D$ と指数 $n$ のアーベル拡大 $L/K$ が，以下のように１対１に対応していることになる、というのがクンマー理論の結論です。

$\begin{array}{c} (K^\times)^n \subset D \subset K^\times, \\ [ D:(K^\times)^n] は有限 \;\; \end{array} \;\; \xrightarrow{\;\;\;L = K(\sqrt[n]{D})\;\;\;} \;\; L/K は指数 n アーベル拡大$

$\begin{array}{c} (K^\times)^n \subset D \subset K^\times, \\ [ D:(K^\times)^n] は有限 \;\; \end{array} \;\; \xleftarrow{\;D = (L^\times)^n \cap K\;} \;\; L/K は指数 n アーベル拡大$

クンマー理論の主定理

このようなセッティングのもと，クンマー理論の主定理が以下の通り成り立ちます。

定理：クンマー理論の主定理

$K$ を $\mu_n$ を含む標数 0 の体とする．

(A): $D$ を $(K^\times)^n \subset D \subset K^\times$ を満たし $[ D:(K^\times)^n]$ が有限である任意の部分群とするとき， $L = K(\sqrt[n]{D})$ とすると， $L/K$ はガロア拡大で，

$D/(K^\times)^n \simeq \mathrm{Gal}(L/K) \tag{1}$

が成り立つ．すなわち， $L/K$ は指数 $n$ のアーベル拡大である．

(B): 逆に， $L/K$ を指数 $n$ の有限次アーベル拡大とするとき， $D = (L^\times)^n \cap K$ とすると， $(K^\times)^n \subset D \subset K^\times$ であり $L = K(\sqrt[n]{D})$ とかける．すなわち， $L/K$ は指数 $n$ のクンマー拡大である．

上記の定理では， $D$ に対応したアーベル拡大 $L/K$ があり，そのガロア群が式 $(1)$ のように「 $D$ と基礎体 $K$ の言葉」でわかりやすくかけるということ（主張 (A)）と，逆にアーベル拡大に対応するべき根拡大の添加元の存在（主張 (B)）の２点を主張しています。

式 $(1)$ の同型は，前回紹介したクンマー・ペアリングによって導かれます。前回の命題 3.3 により

$\begin{array}{ccc} D/(K^\times)^n & \simeq & \mathrm{Hom}\left(\mathrm{Gal}(L/K), \; \mu_n\right), \\ x(K^\times)^n & \longmapsto & \left( \tau \mapsto (\tau, x(K^\times)^n)\right) \end{array}$

が成り立つことを思い出します。これが同型になることは，命題 3.3 の証明で，特に $D/(K^\times)^n = \langle c(K^\times)^n \rangle$ の場合に限定して確認しています。

また， $L/K$ がアーベル拡大で指数 $n$ なので（ガロア群 $\mathrm{Gal}(L/K)$ の任意の元の位数が $n$ を割り切る）

$\mathrm{Hom}\left(\mathrm{Gal}(L/K), \; \mu_n\right) \simeq \mathrm{Gal}(L/K)$

より，

$D/(K^\times)^n \simeq \mathrm{Gal}(L/K) \tag{1 再掲}$

が成り立ちます。これで式 $(1)$ が導かれました。

式 $(1)$ を見たときに，私は「円分体論」の

$\mathbb{Z}/m\mathbb{Z} \simeq \mathrm{Gal}(\mathbb{Q}(\mu_m)/\mathbb{Q})$

の式や「不分岐類体論」の

$I_K/P_K \simeq \mathrm{Gal}(L/K)$

を思い出しました。まだ，明確に言語化できませんが，これらの間には深いところでつながっている気がします。

以上の議論は抽象的で掴みづらいかと思います（私がよくわからなかった）ので，いくつか具体例を作って理解していくことにしましょう。

例１：

まずは基本的な例から考えましょう。前回考えたものと同様のケースとして $D = \langle c \rangle (K^\times)^n$ とします。 $c$ は，ちょうど $n$ 乗して $n$ 乗数となる $K^\times$ の元と仮定します。

記号の意味ですが， $\langle c \rangle$ は $c$ により生成される群を表します。なので， $D$ は「 $c^k \delta^n$ とかける数の集合」です。 $k\in \mathbb{Z}$ で $\delta \in K^\times$ です。

ここで， $(K^\times)^n \subset \langle c \rangle (K^\times)^n \subset K^\times$ であることを確認します。 $k = 0$ とすれば， $(K^\times)^n$ に一致するので， $\langle c \rangle (K^\times)^n$ は明らかに $(K^\times)^n$ を含みます。

このとき，

$D/(K^\times)^n = \langle c(K^\times)^n \rangle$

です。また，右辺は明らかに $n$ 次の巡回群ですから（ $c(K^\times)^n = (K^\times)^n$ なので），

$D/(K^\times)^n = \langle c(K^\times)^n \rangle \simeq \mathbb{Z}/n\mathbb{Z}$

が成り立ちます。

また， $L = K(\sqrt[n]{c})$ より，主定理から

$D/(K^\times)^n \simeq \mathrm{Gal}(L/K)$

が成り立ちます。

結局，

$\mathrm{Gal}(L/K) \simeq \mathbb{Z}/n\mathbb{Z}$

であることが導かれました。巡回拡大ですね。

例２：

今度は $D = \langle c_1, c_2 \rangle (K^\times)^n$ とします。 $c_1, c_2$ は，それぞれちょうど $n$ 乗して $n$ 乗数となる $K^\times$ の元で， $c_1$ と $c_2$ は互いに素と仮定します。

$\langle c_1, c_2 \rangle$ は $c_1, c_2$ により生成される群を表します。なので， $D$ は「 $c_1^{k_1} c_2^{k_2} \delta^n$ とかける数の集合」です。 $k_1, k_2 \in \mathbb{Z}$ で $\delta \in K^\times$ です。

また， $(K^\times)^n \subset \langle c_1, c_2 \rangle (K^\times)^n \subset K^\times$ であることが確認できます。

このとき， $c_1, c_2$ が互いに素より

$D/(K^\times)^n = \langle c_1(K^\times)^n, c_2(K^\times)^n \rangle \simeq \mathbb{Z}/n\mathbb{Z} \oplus \mathbb{Z}/n\mathbb{Z}$

が成り立ちます（２つの巡回群の直和となる）。

また， $L = K(\sqrt[n]{c_1}, \sqrt[n]{c_2})$ より，主定理から

$D/(K^\times)^n \simeq \mathrm{Gal}(L/K)$

が成り立ちます。

結局，この場合は

$\mathrm{Gal}(K(\sqrt[n]{c_1}, \sqrt[n]{c_2})/K) \simeq \mathbb{Z}/n\mathbb{Z} \oplus \mathbb{Z}/n\mathbb{Z}$

が言えたことになりますね。

例３：双２次拡大

$n = 2$ のときを考えましょう。 $\mu_2 = \{\pm 1\}$ より， $\mathbb{Q} \supset \mu_2$ ですから， $\mathbb{Q}$ 上のクンマー拡大を考えることができます。

というわけで， $K = \mathbb{Q}$ とします。 $D = \langle c_1, c_2 \rangle (\mathbb{Q}^\times)^2$ とします。 $c_1, c_2 \in \mathbb{Q}^\times$ は平方数でない（square-free）数で， $c_1$ と $c_2$ は互いに素と仮定します。 $\langle c_1, c_2 \rangle (\mathbb{Q}^\times)^2$ は， $c_1^{k_1} c_2^{k_2} \delta^2$ とかける数の集合です。 $(\mathbb{Q}^\times)^2 \subset \langle c_1, c_2 \rangle (\mathbb{Q}^\times)^2 \subset \mathbb{Q}^\times$ であることが確認できます。

このとき， $c_1, c_2$ が互いに素より

$D/(\mathbb{Q}^\times)^2 = \langle c_1(\mathbb{Q}^\times)^2 , c_2(\mathbb{Q}^\times)^2 \rangle \simeq \mathbb{Z}/2\mathbb{Z} \oplus \mathbb{Z}/2\mathbb{Z}$

であることがわかります。右辺はいわゆる「クラインの四元群」と言われる群ですね。

$L = \mathbb{Q}(\sqrt{c_1}, \sqrt{c_2})$ より，主定理から

$D/(\mathbb{Q}^\times)^n \simeq \mathrm{Gal}(L/\mathbb{Q})$

となり，結局

$\mathrm{Gal}(\mathbb{Q}(\sqrt{c_1}, \sqrt{c_2})/\mathbb{Q}) \simeq \mathbb{Z}/2\mathbb{Z} \oplus \mathbb{Z}/2\mathbb{Z}$

が言えます。２つの平方根による拡大を双２次拡大というそうです。

例４：２次体

「２次体（ $\mathbb{Q}$ 上の２次拡大体）」もクンマー理論に含まれます。

$n = 2, \; K = \mathbb{Q}$ とし， $D = \langle c \rangle (\mathbb{Q}^\times)^2$ とします。ここで， $c \in \mathbb{Q}^\times$ は平方数でない（square-free）数と仮定します。 $(\mathbb{Q}^\times)^2 \subset \langle c \rangle (\mathbb{Q}^\times)^2 \subset \mathbb{Q}^\times$ であることは明らかです。

このとき，

$D/(\mathbb{Q}^\times)^2 = \langle c(\mathbb{Q}^\times)^2 \rangle \simeq \mathbb{Z}/2\mathbb{Z}$

であることがわかります。右辺は２次巡回群ですから，２次拡大ですね。

$L = K(\sqrt{c})$ より，主定理から

$D/(\mathbb{Q}^\times)^n \simeq \mathrm{Gal}(L/\mathbb{Q})$

となり，結局

$\mathrm{Gal}(\mathbb{Q}(\sqrt{c})/\mathbb{Q}) \simeq \mathbb{Z}/2\mathbb{Z}$

が言えます。

今，主張 (A)を用いて $\mathbb{Q}$ に $\sqrt{c}$ を添加するとガロア群が２次巡回群であることを示しました。

この逆を考えましょう。すなわち，主張 (B)より， $\mathbb{Q}$ 上の指数 $2$ のアーベル拡大 $L/\mathbb{Q}$ を考えます。

このとき， $D = (L^\times)^2 \cap \mathbb{Q}$ とすると， $L = \mathbb{Q}(\sqrt{D})$ と表せます。

$D/(\mathbb{Q}^\times)^2$ の完全代表系を $\{c_1, c_2, c_3, \cdots, c_t\}$ とすると，

$L = \mathbb{Q}( \sqrt{D} ) = \mathbb{Q}( \sqrt{c_1}, \sqrt{c_2}, \sqrt{c_3}, \cdots , \sqrt{c_t} )$

と表せます。

したがって， $\mathbb{Q}$ 上の任意の指数 $2$ のアーベル拡大は， $\mathbb{Q}$ にsquare-freeな数の平方根を添加することによって得られることがわかりました。２次体はこの特別な場合ですから，２次体も平方根の添加によって得られることがわかりました。

以上の議論から，２次体の基本的事実である「すべての２次体は square-freeな数 $c$ が存在して $\mathbb{Q}(\sqrt{c})$ の形でかける」が示せました。面白いですね！

例５：「 $\sqrt{2} + \sqrt{3} + \sqrt{5} + \sqrt{7}$ は無理数」の証明

最後の例として面白い応用を紹介します。以前，せきゅーんさんが
integers.hatenablog.com

の記事で「 $\sqrt{2} + \sqrt{3} + \sqrt{5} + \sqrt{7}$ は無理数」の証明はクンマー理論を使えばできる，と注釈していたことを思い出しました。私は当時その意味を理解していませんでしたが，今回やっとわかったと感じたので，自分なりにまとめてみたくなりました。

（証明）
先程と同様に， $n = 2$ として $K = \mathbb{Q}$ の場合のクンマー理論を考えます。

$D = \langle 2, 3, 5, 7 \rangle (\mathbb{Q}^\times)^2$ とします。 $D$ は「 $2^{k_1} 3^{k_2} 5^{k_3} 7^{k_4} \delta^{2}$ とかける数の集合」です。 $2, 3, 5, 7$ はどれも平方数ではないので，条件を満たします。もちろん， $(\mathbb{Q}^\times)^2 \subset \langle 2, 3, 5, 7 \rangle (\mathbb{Q}^\times)^2 \subset \mathbb{Q}^\times$ です。

このとき，

$D/(\mathbb{Q}^\times)^2 = \langle 2(\mathbb{Q}^\times)^2, 3(\mathbb{Q}^\times)^2, 5(\mathbb{Q}^\times)^2, 7(\mathbb{Q}^\times)^2 \rangle \simeq \mathbb{Z}/2\mathbb{Z}^{\oplus 4}$

であることがわかります。

また， $L = \mathbb{Q}(\sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7})$ より，主定理から

$D/(\mathbb{Q}^\times)^n \simeq \mathrm{Gal}(L/\mathbb{Q})$

となり，

$\mathrm{Gal}(\mathbb{Q}(\sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7})/\mathbb{Q}) \simeq \mathbb{Z}/2\mathbb{Z}^{\oplus 4}$

が言えます。したがって，拡大次数は

$\left[ \mathbb{Q}(\sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7}) \; \colon \; \mathbb{Q} \right] = 2^4$

であることがわかる。

一方， $\mathbb{Q}(\sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7})/\mathbb{Q}$ の基底の候補は，

$\begin{align} 1, \sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7}, \sqrt{2\cdot 3}, \sqrt{2\cdot 5}, \sqrt{2\cdot 7}, \sqrt{3\cdot 5}, \sqrt{3\cdot 7}, \sqrt{5 \cdot 7} , \\ \sqrt{2\cdot 3\cdot 5}, \sqrt{2\cdot 3\cdot 7}, \sqrt{2\cdot 5\cdot 7}, \sqrt{3\cdot 5\cdot 7}, \sqrt{2\cdot 3\cdot 5\cdot 7}\end{align}$