ラングレーの問題とフランクリンの凧

この記事は 明日話したくなる数学豆知識アドベントカレンダー の 11 日目の記事です。（ 10 日目：ステップ関数の微分）

これまで End01nojo さんと二人で続けてきた「明日話したくなる数学豆知識アドベントカレンダー」に、なんと新たな加勢が！がんばった甲斐がありました。どんな記事を書いてもらえるのか今から楽しみです♪

さて、tsujimotter の最近の投稿は数式ばかりの記事でしたので、たまには気分を換えて幾何学のお話でも。

《ラングレーの問題》
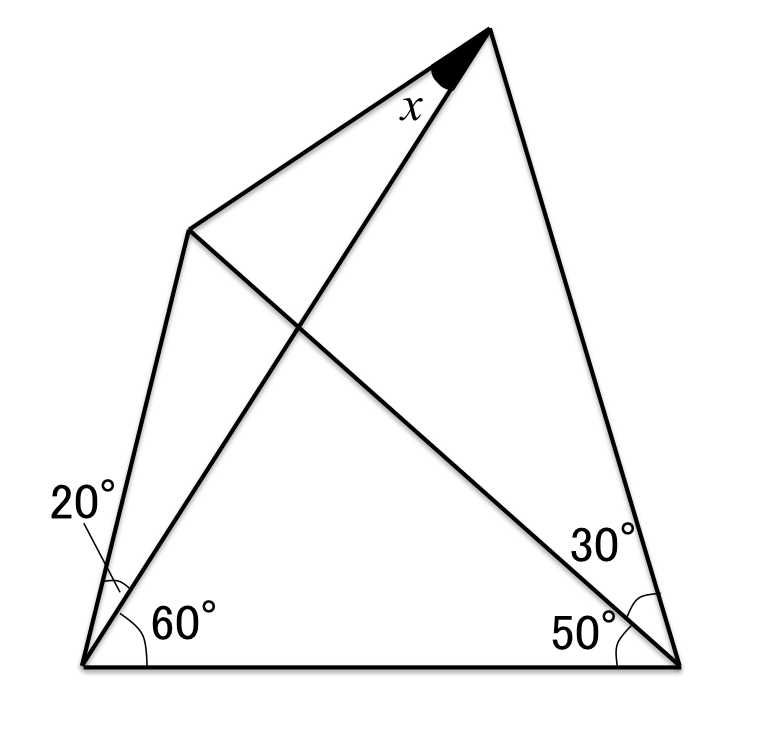
以下の図のように、角度 20°, 60°, 50°, 30° が与えられたとき、 の角度を求めよ。

この問題、答えは教えないのでぜひ頭を使って解いてみてください。
中学生でも原理的には解けるレベルの問題ですが、大学生でもなかなか難しい問題です。「たかが初等幾何学」と思っていると、痛い目を見ます。

ヒントは「アクロバティックな補助線」です。あんまりヒントになってないか。笑
ふつうに考えて解けないときには、元の線を無視してみるのもよいかもしれません。

解けた暁には、周りの人にドヤ顔で自慢してもいいでしょう。飲み会で話したときには、みんな無言で考え出すこと請け合いです。

ラングレーの問題とは

今回は角度として 20°, 60°, 50°, 30° を用いました。一般に、それらを整数 を使って °, °, °, ° とした問題の総称を「ラングレーの問題」と呼びます。ラングレーという数学者が、1922年に The Mathematical Gazette 誌にコラムとして投稿したのがはじまりで、日本では数学セミナー誌 1967 年 6 月号の「エレガントな回答をもとむ」欄ではじめて紹介されました。

ラングレーの問題の最大の特徴は、その 膨大なパターン と 解法の複雑さ です。
一見１つ解法が見つかれば、すべてのラングレーの問題が解けそうな気がしてしまいますが、それは大きな誤解です 。非常に面白いことに、問題が異なれば解法もまったく違ったものになります。すなわち、角度が異なった２つのラングレーの問題に対しては、同じような解法が使えないことが多いのです。

フランクリンの凧とは

冒頭の問題に対して用いることが出来る解法（の１つ）に付けられた名前です。このワードで検索してみると、たくさん解法が出てきます。気になる方は探してみてください。

ベンジャミン・フランクリンが、雷の中で凧揚げをした有名な実験から付けたのだと思います。そういえば、最近缶コーヒーの側面に、ベンジャミン・フランクリンの名言を見つけましたよ。

この言葉は、彼が言うと重みがありますね。いろんな意味で。

参考文献

膨大な時間をかけて、ラングレーの問題のすべてのパターンについて解法をまとめられた（おそらく世界初の）作品です。驚くべきことに、著者の斉藤さんは本職の数学者ではありません。ラングレーの問題の面白さに魅せられて、独学で研究してまとめられたのだとか。いったいどこからその情熱が生まれてくるのか。本のタイトルも魅力的ですね。

ラングレーの問題にトドメをさす!―4点の作る小宇宙完全ガイド