日曜数学Advent Calendar 2020最終日の記事です。投稿してくださったみなさま、ありがとうございます!!!
adventar.org
目次:
1. 今日のテーマ
最終日の今日は 「今年一番興奮した話」 を書いてみようと思います。いったいどんな数学に興奮したのか、その背景について説明させてください。
tsujimotterの日曜数学の楽しみ方は、数学の理論を本で勉強して楽しむことです。日曜数学を楽しむ方の中には問題やパズルを解いて楽しむ方もいると思うのですが、私はあまり好きではありませんでした。
好きではないというより、どちらかといえば得意ではないという感じです。たいていの場合、自力で解けないので、粘ってもわからずじまいで飽きてしまうのですね。結局、答えを見て楽しむほうが自分には合っているのだと、少なくとも2019年の時点ではそう思っていました。
ところが、今年どうしても自力で解きたい数学の問題が出てきたのです。それが「数学ゴールデン」という漫画に出てきた問題です。数学ゴールデンは、数学オリンピックを目指す高校生の物語です。2020年に単行本第1巻が発売されたばかりの新しい数学漫画です。
作中では、実際に数学オリンピックに出てくるような難問が紹介されます。その最初の問題が今回扱いたい問題です。引用してみましょう。
その手紙では 3つの話題のみが やりとりされている.
そして、同じ2人組の間でなされる話題は常に同じ一つのやりとりである.このとき、互いに同じ話題の手紙のやりとりをした3人組が存在することを証明せよ.
(IMO 1964)
この問題は ラムゼーの定理 という有名な定理を背景とする問題です。1964年の国際数学オリンピック本戦で、実際に出題された問題なのだそうです。
せっかくなので、ただ読むだけでなく自分でも解いてみようと思いました。答えを見ずに自力で解けるまで頑張って、解けたら次のページに進むようにしてみようと。
普段の私だったら自分で解こうとは思えなかったと思いますが、今回は違いました。というのも、以前聞いた数学の講演*1 で、この問題のより簡単な類似(後述)があることを知っていたからです。その類似問題なら自分の力でも解けるかもしれない。そう思ってしまったのです。
そして なんと自分の力で解くことができました。
最初は泥臭い解法でした。しかし、考えていくうちに、だんだんと洗練された解法に近づいていきました。最終的に、その方法を一般化して、元々の問題を解くことができてしまったのです。
この体験は本当に感動しました。記憶している限りでは、今年一番興奮した出来事でした。
そんなわけで今日のブログでは、上で紹介した数学ゴールデンの問題について、私が解答に至ったステップを紹介したいと思います。
最終的な洗練された解法だけ紹介しても良いわけですが、そんな解説はありふれていますし、なんなら数学ゴールデンの本文を読んでいただければ分かります。
私にしか書けないのは、私の感動を追体験できるようにまとめた記事 です。
元々の問題の解法を知らない方に、この記事の おすすめの読み方 を紹介します。まずは第1節(本セクション)を読んだ上で、一旦止めて自分の頭で定理2の証明を考えてみてください。それで、どうしてもわからないということになったら、ちょっとずつ読み進めてみてください。
簡単には最終的な回答にたどり着かないようになっていますので、少しくらい読んだとしても「ネタバレ」にはならないかと思います。年末の日曜数学のお供に、ぜひじっくり楽しんでいただけたら幸いです。
さて、いきなり数学ゴールデンの問題に直接挑む前に、問題をより簡単にしてみたいと思います。
まず、上の問題は「手紙のやり取り」という体をとっていますが、本質的にはグラフの辺の彩色問題です。
頂点が 個の完全グラフを考えます。完全グラフとは、すべての頂点の間に辺があるグラフのことです。
個の頂点のグラフでは、
個の辺があることになります。
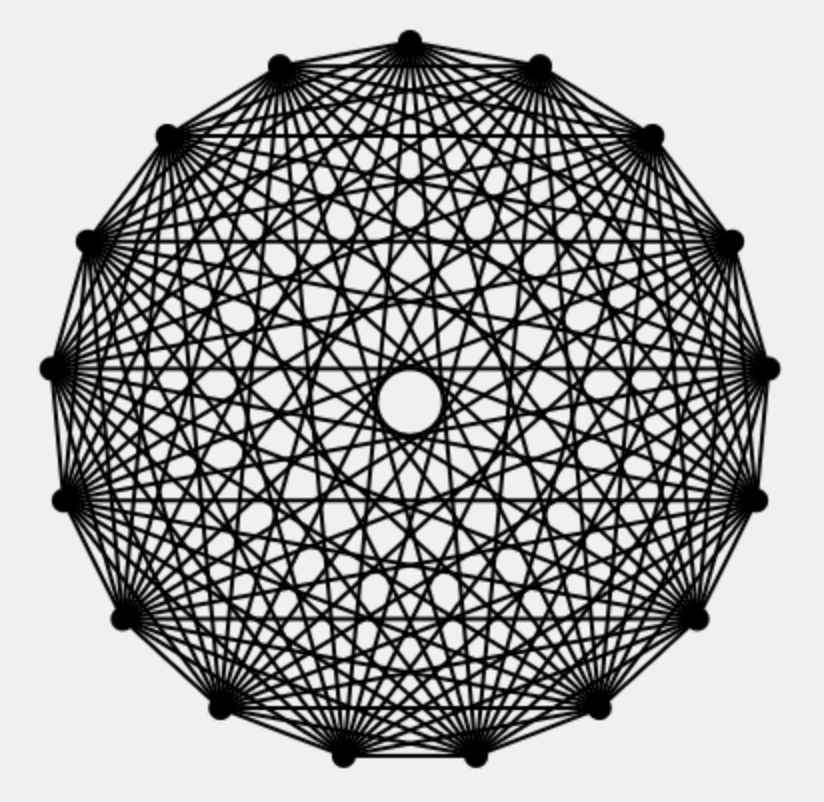
頂点が「人」を表していて、辺が「手紙のやり取り」を表しています。
この完全グラフのすべての辺に対し 色の色を塗ることを考えます。それぞれの色がやり取りされる「話題」を表しているわけです。
3つの頂点の作る三角形に着目したとき、その三角形のすべての辺が同じ色であるような三角形を同色三角形と呼ぶことにします。同色三角形が「互いに同じ話題の手紙のやりとりをした3人組」を表すわけですね。
このように置くと、数学ゴールデンの問題は次の定理を証明する問題として言い換えられます:
これが証明できるはずなのです。しかしながら、いきなり扱うには、少し頂点の数や色の数が多すぎますね。もう少し問題を簡単にしてみましょう。
実際、色の数を 色に減らすと、頂点数を
にした次の定理が成り立ちます。
実際、頂点数 のグラフを描いて、辺を2色で塗り分けようとすると、たしかに同色三角形ができてしまいます。
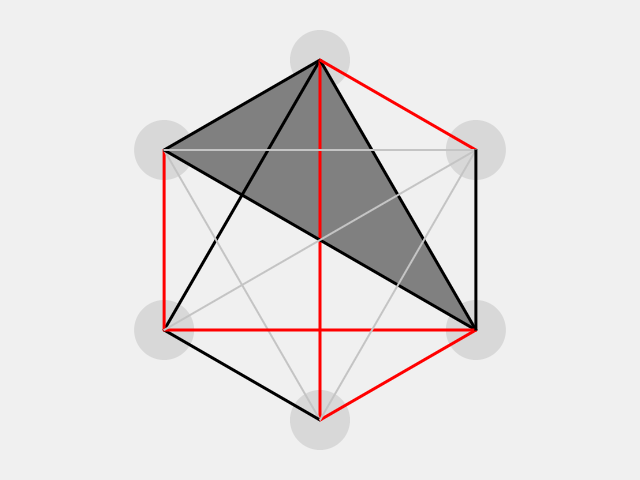
頂点の個数は なので、辺の個数は
です。色として (黒色)・
(赤色)の2色を割り当てることにすると
通りです。あとはこれらを全探索すればよいことになります。
すなわち、各辺に対して または
を割り当てる2分木を考えて、すべての場合について検討すれば良いという事ですね。
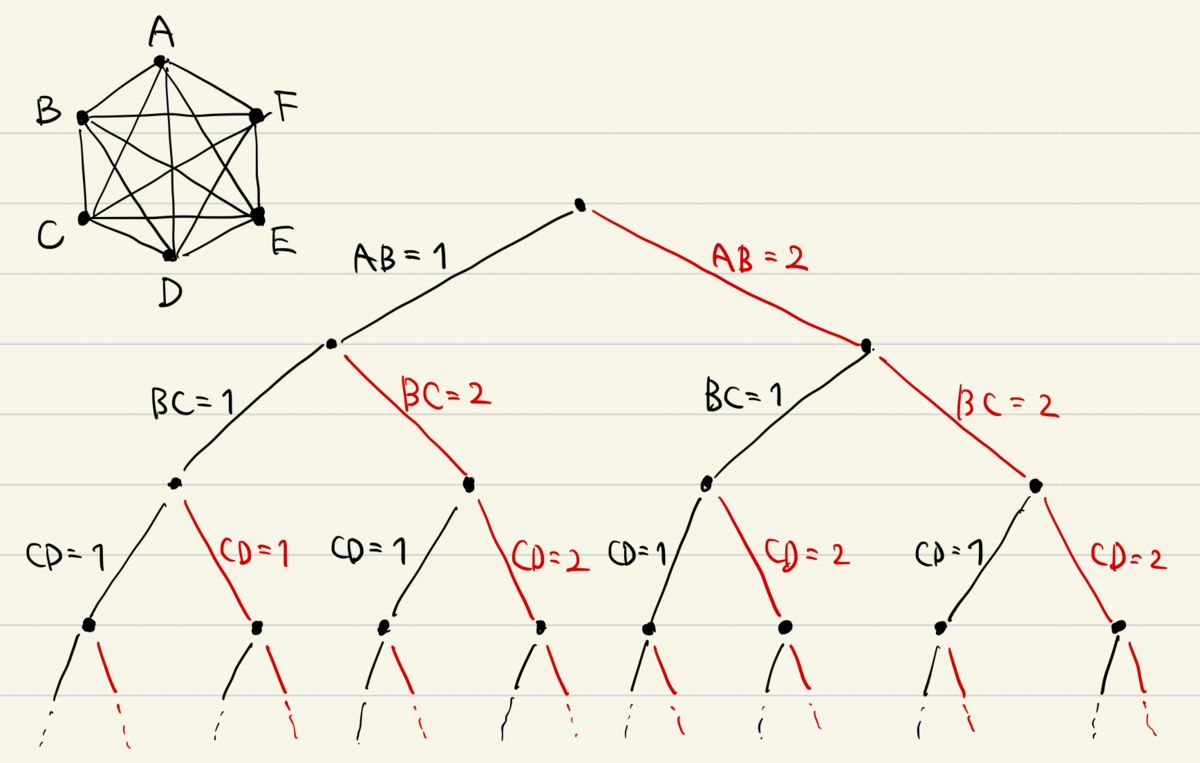
もちろん、全て探索する必要はなく、ある程度「枝刈り」をすることでかなり分岐を減らす事ができそうです。これなら解けそうな気がしませんか。
実際に問題を考える上では、毎回ノートに図を書いていくのはなかなか大変です。私も何度か図を書きましたが、辺の数が多く、だんだんとやっていられなくなりました。
そこで開発したのがこのアプリです!
tsujimotter.info
以下のツイートの動画のように、頂点の付近の円をクリックしてから、また別の頂点をクリックすると、2頂点の間の辺が塗られます。下のチェックボタンで1, 2, 3, 4のいずれかを選択することで、塗る色を変えることができます。"ー" で色をクリアできます。
「ラムゼー問題」のチェックをするのが大変だったので、ブラウザで確認できるアプリを作ってみました!
— tsujimotter 日曜数学者 (@tsujimotter) 2020年7月3日
ぜひ遊んでみてください!
(デフォルトは n = 6 ですが、左上のメニューでnの値も変えることができます)
Ramseyhttps://t.co/cBY3zD5g5h pic.twitter.com/7x8FTuhYCV
下図のように「3辺が同じ色で塗られた三角形」があると色がつきます。
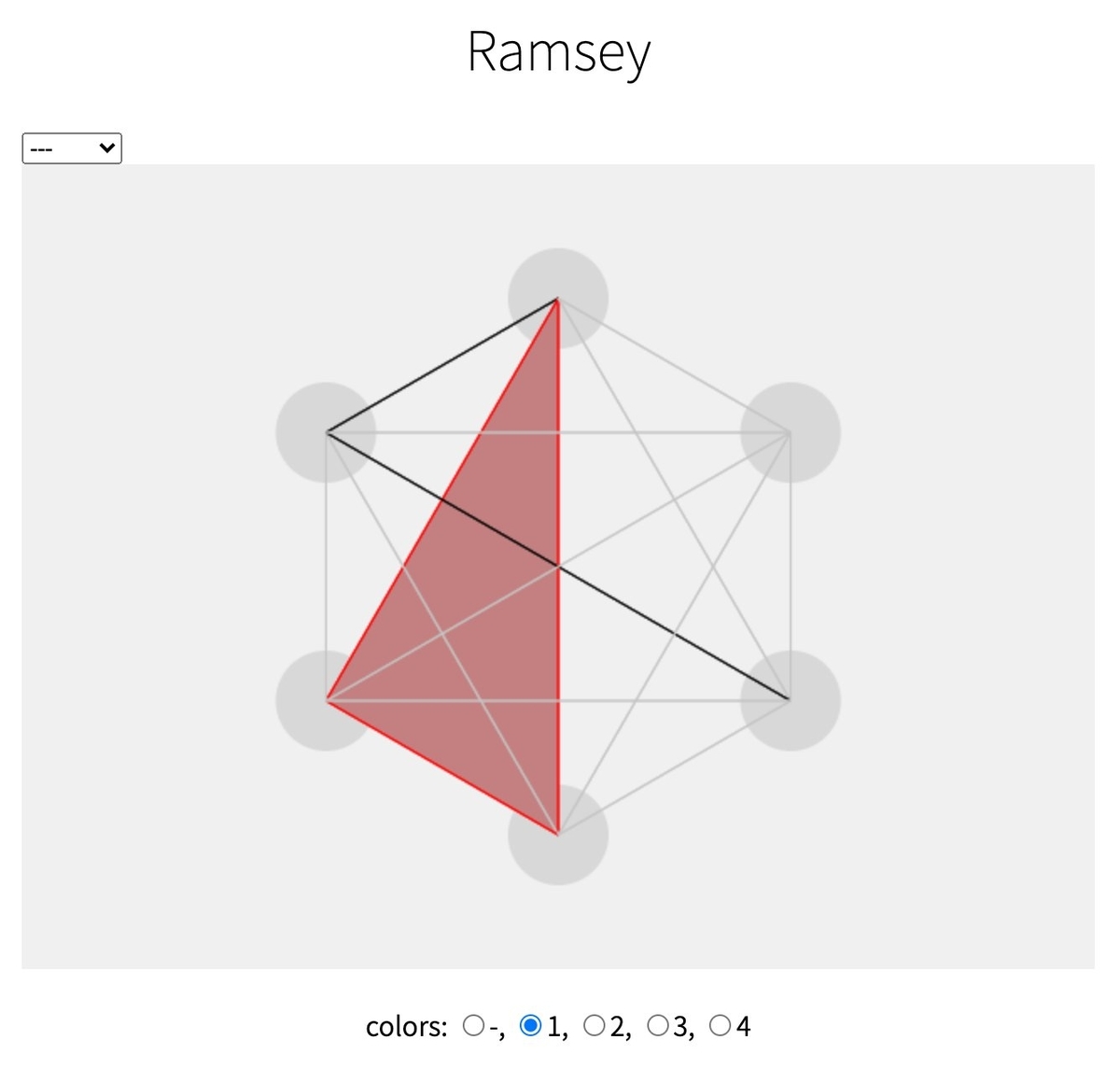
左の上のメニューから、n = ? を選択すると、頂点数を3〜20の間で変えることができます。デフォルトの画面では頂点数は6ですが、元々の頂点数17の問題を扱うこともできます。
ぜひ遊んでみてください!
2. 気合いで全探索する方法(解法1)
それでは定理2について、私が何も見ないで考えた最初の証明をご紹介しましょう。
この方法はまったくもって洗練されたものではないので、この証明を紹介すること自体にあまり意味はないかと思います。とにかく解けた事が嬉しかったのと、こんな泥臭い方法でもうまくいくということの一種の証明のため、今回紹介してみたいと思います。
まず、6頂点 を反時計回りに正六角形状に並べて、辺
を順に
と名付けることにします。
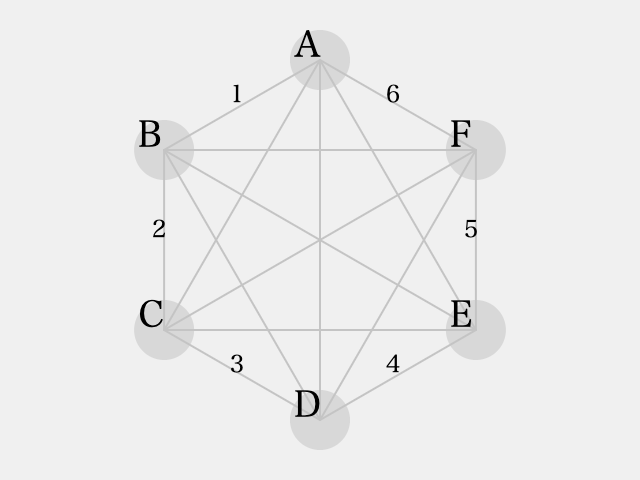
辺 〜
のすべてに
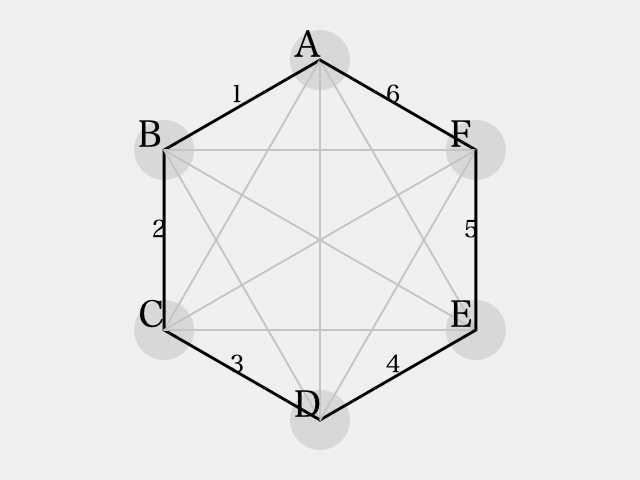
を割り当てることを
と表現することにすると、次の図のようになります。(図では
を黒色、
は赤色で表現しています。)
ここで、辺 を2辺とする三角形を考えます。残り一辺に色
を割り当ててしまうと、3辺が同色であるような三角形(同色三角形)ができてしまいます(下図)。
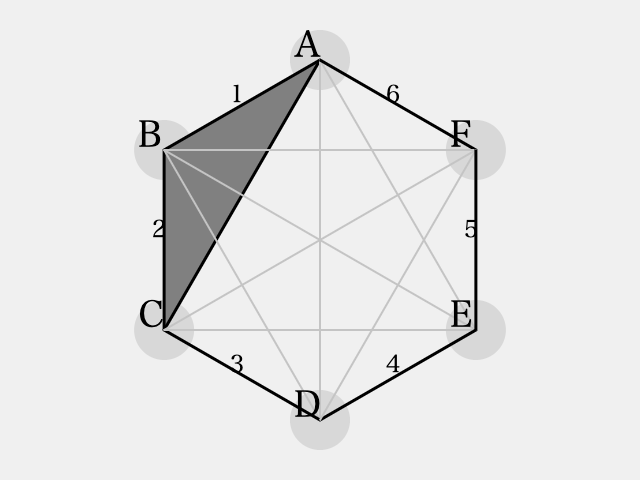
したがって残り1辺は を割り当てる他ありません。すると、次のような図が出来上がるわけですが、同色三角形ができることがわかります。
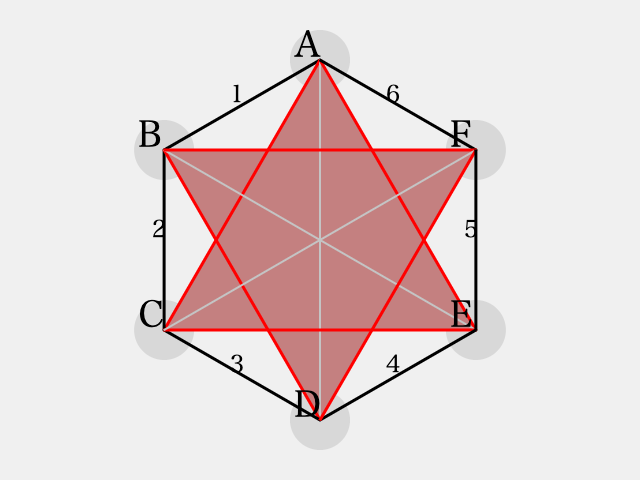
よって、 のパターンからは、どうやっても同色三角形ができてしまいます。
こんな調子で、辺 〜
に任意の色を割り当てたときに、どの組み合わせも同色三角形を作ってしまうことを示せばよいわけですね。
それでは、こんな方針でいけるのかやってみましょう。
(証明)
グラフの頂点 を反時計周りに正六角形状にならべ、辺
に対して
と番号をつける。番号
の辺の色を
とし、彩色のパターンを組
によって表す。
のパターン:
前述の通り、同色三角形を避けた彩色は不可能である。
のパターン:
まず、初期状態はこうなります:
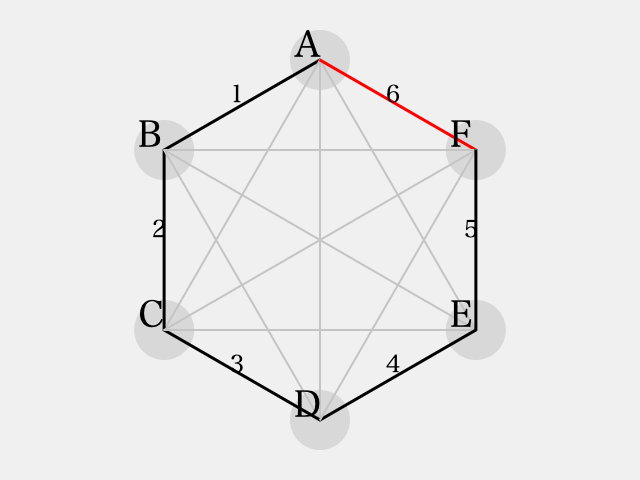
三角形 は、2辺が
で彩色されている。したがって、同色三角形を避けるためには、残り1辺は
で彩色されなければならない。(図は
を黒色、
を赤色としている)
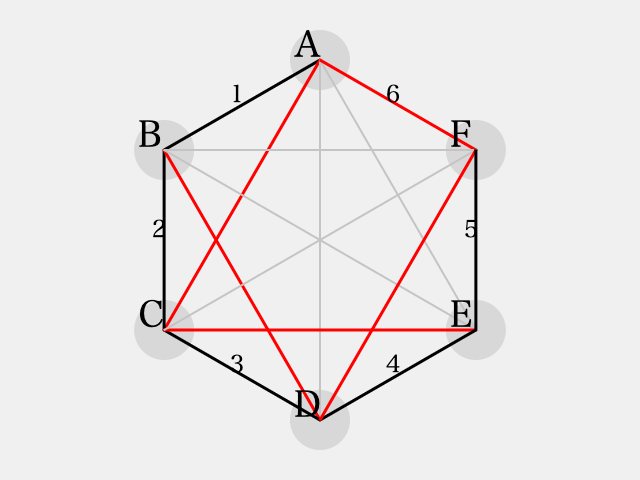
三角形 は、同様に2辺が
で彩色されている。よって、同色三角形を避けるためには、残り1辺は
で彩色されなければならないが、これにより同色三角形
ができあがる。ゆえに、同色三角形を避ける事ができない。
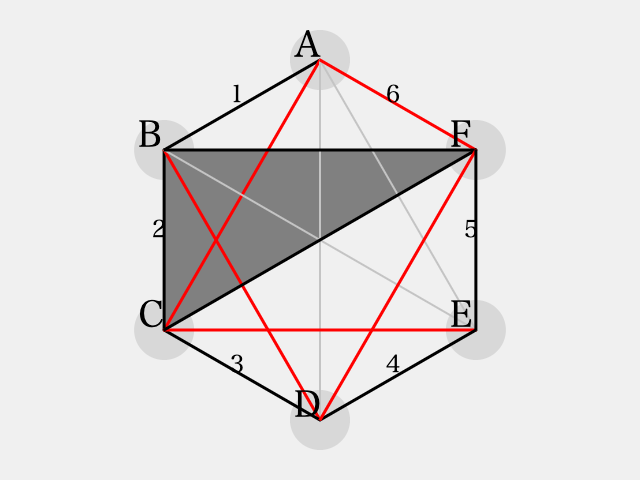
のパターン
まず、初期状態はこうなります:
三角形 はそれぞれ2辺が
で彩色されているため、残り1辺を
で彩色する。
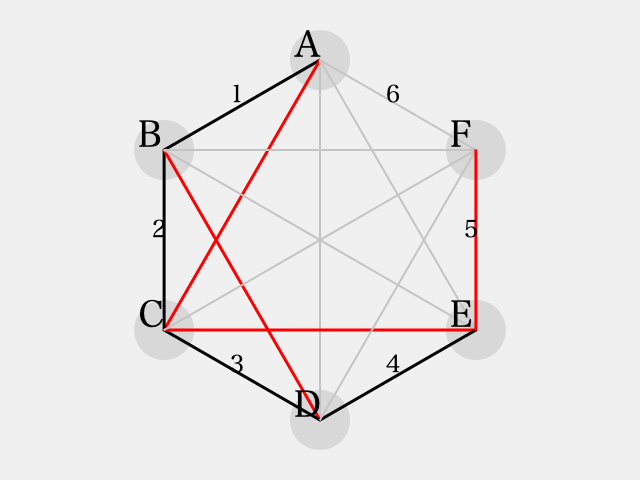
ここで、三角形 に着目すると、
は
で彩色される。このとき、三角形
を考察すると、
が
で彩色されなければならないが、これにより同色三角形
ができあがるため、同色三角形を避ける事ができない。
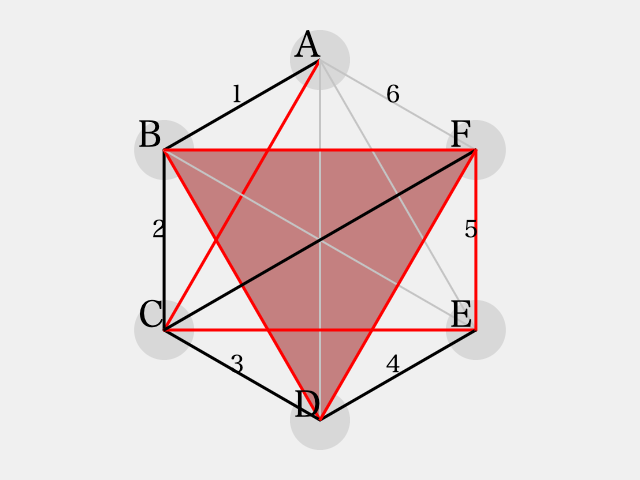
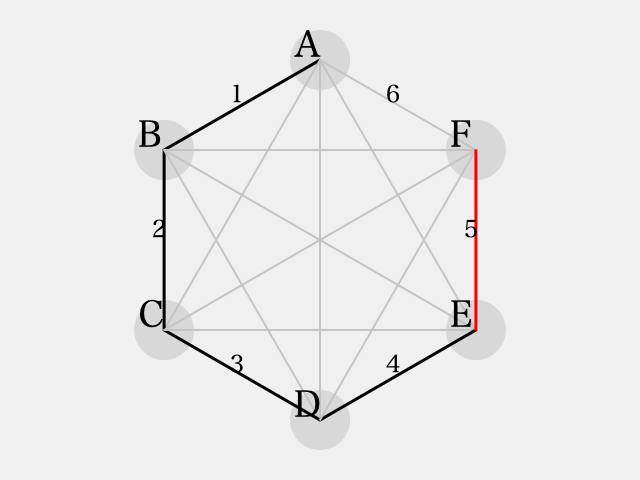
のパターン
まず、初期状態はこうなります:
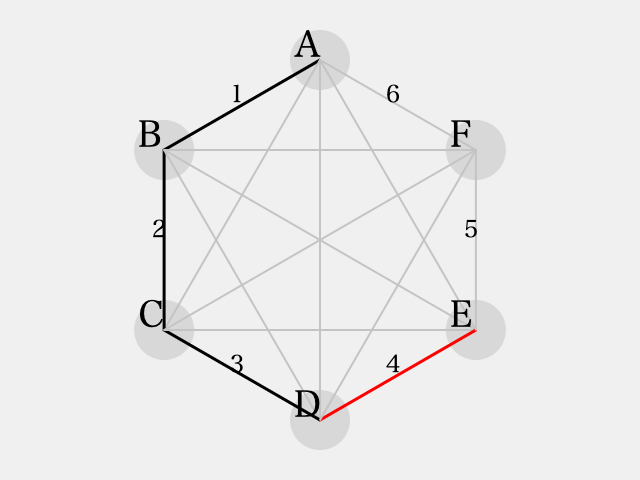
三角形 に着目すると、それぞれ2辺が
で彩色されているので、残りの1辺は
で彩色されます。
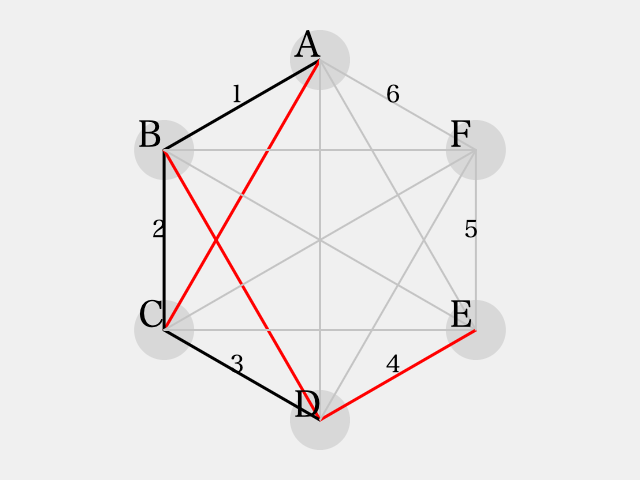
このとき、三角形 に着目すると辺
が
に彩色される。続いて三角形
に着目すると、辺
が
に彩色される。
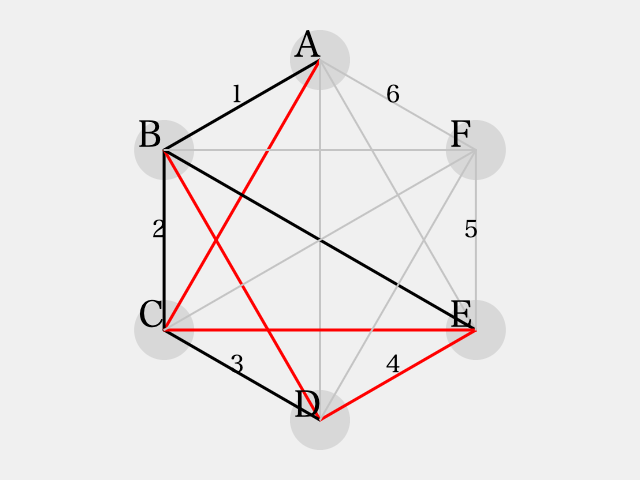
ここで、辺 については、
を彩色すると三角形
が同色に、
を彩色すると
が同色になるため、同色三角形を避ける事ができない。
のパターン
(このケースはちょっと複雑なのでいくらか省略します。)
まず、初期状態はこうです:
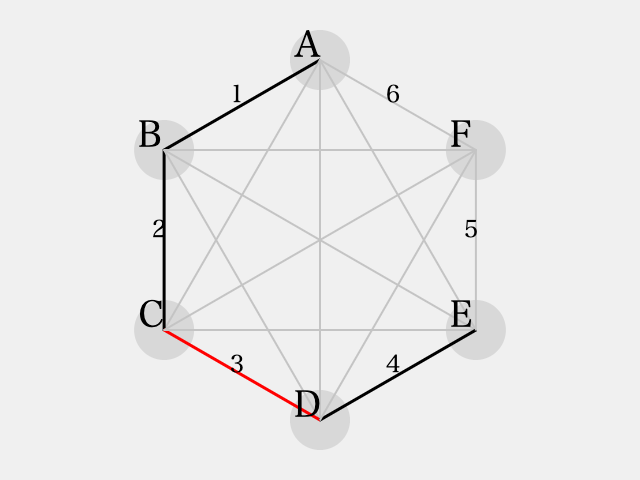
前節までと同じような議論により、次の状態まで自動的に彩色できる。
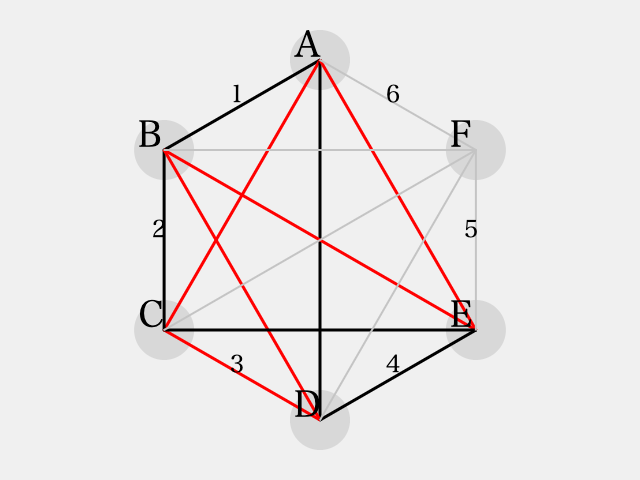
ここで、 のときと
のときで場合分けが発生する。
のとき、三角形
に着目して辺
が
で彩色される。ここで、辺
はどちらの色を彩色しても同色三角形を避ける事ができない。
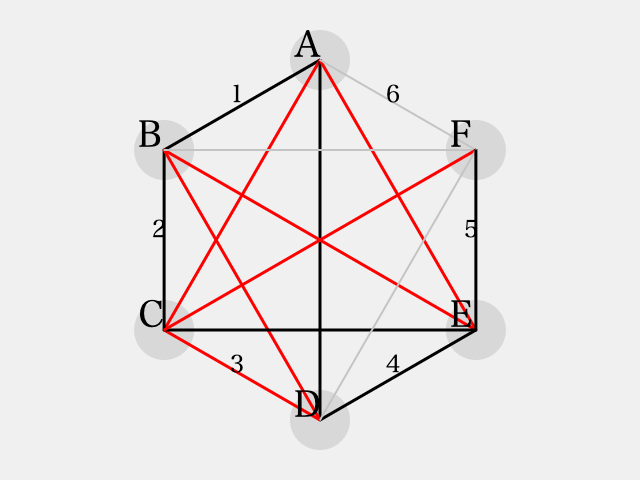
のとき、三角形
に着目して辺
が
で彩色される。ここで、辺
はどちらの色を彩色しても同色三角形を避ける事ができない。
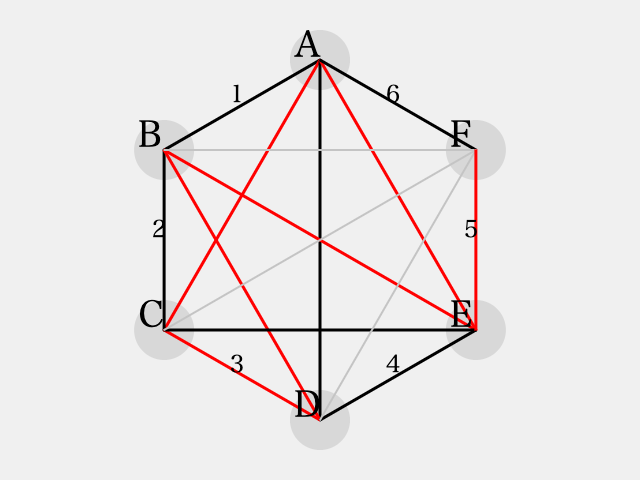
ゆえに、いずれの場合でも同色三角形を避ける事ができない。
のパターン
まず、初期状態はこうです:
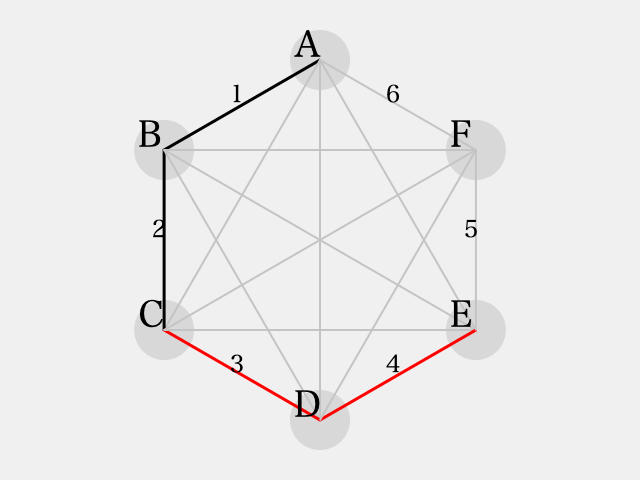
三角形 に着目すると、辺
が彩色できる。
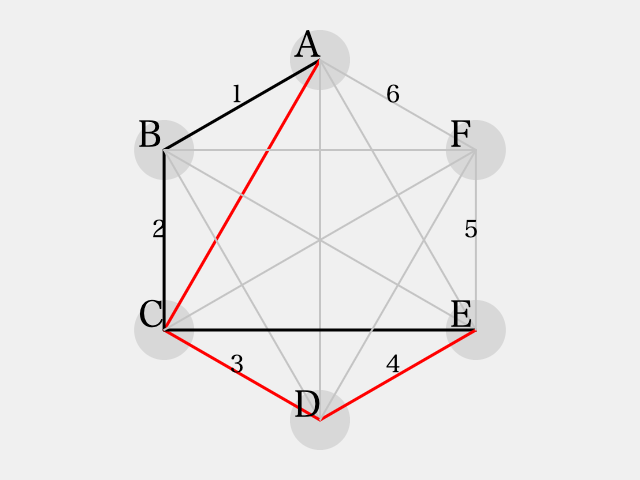
次に、三角形 に着目すると、辺
が彩色できる。
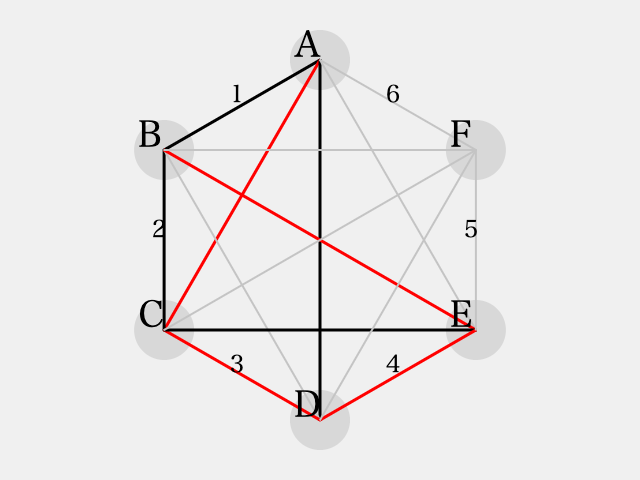
ここで、 にいずれの色を塗ったとしても同色三角形を避ける事ができない。
のパターン
まず、スタートは次の状態から始まる。
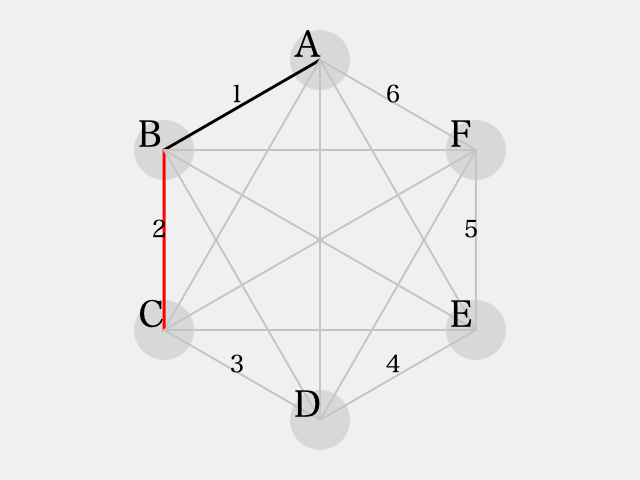
ここで、 とすると
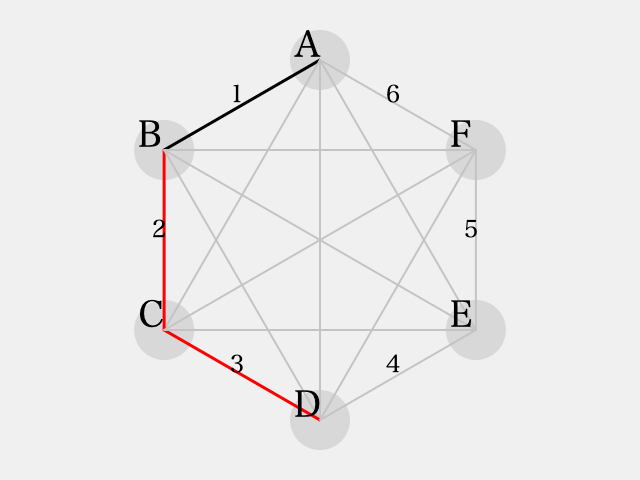
となり、これは の色が反転したパターンとなり、同色三角形を避ける事ができない。
よって、 となる。
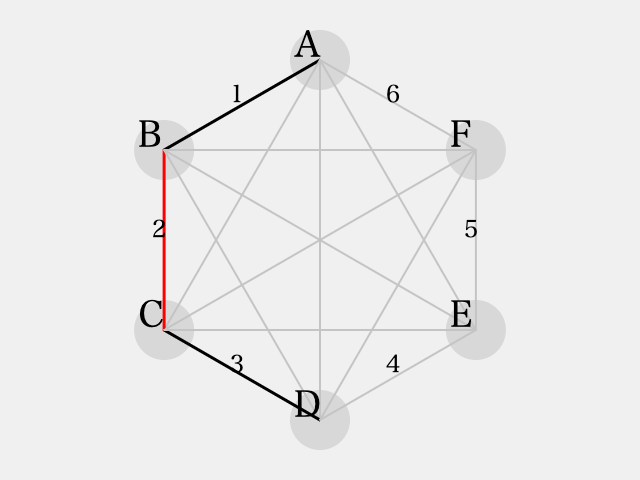
続いて、 とすると
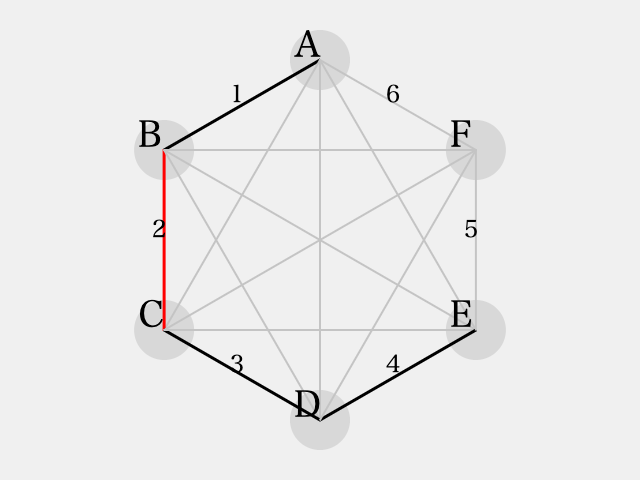
となり、これは のパターンとなり、同じく同色三角形を避ける事ができない。
よって、 となる。
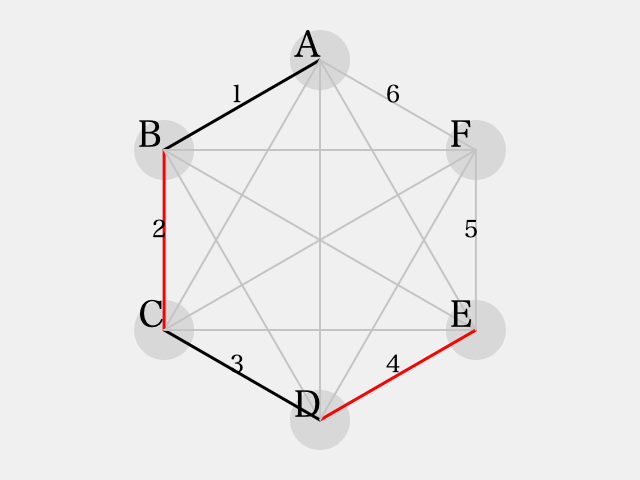
さらに、 とすると
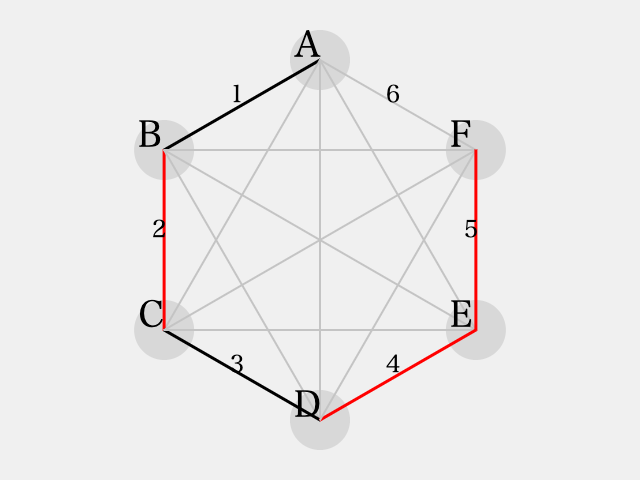
となり、これもやはり の反転パターンとなり、同色三角形を避ける事ができない。
よって、 となる。
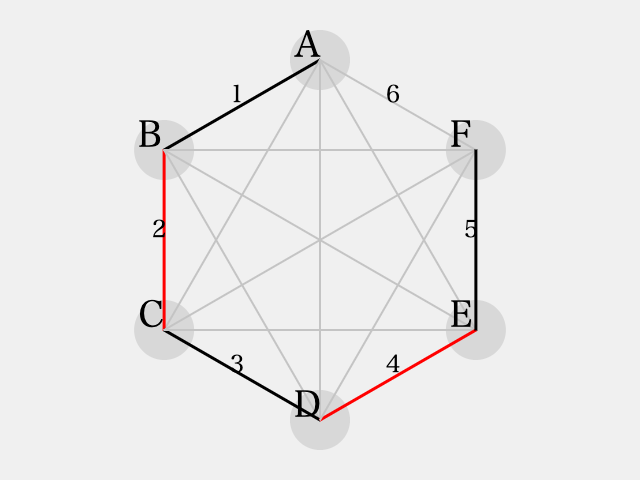
最後に、 とすると
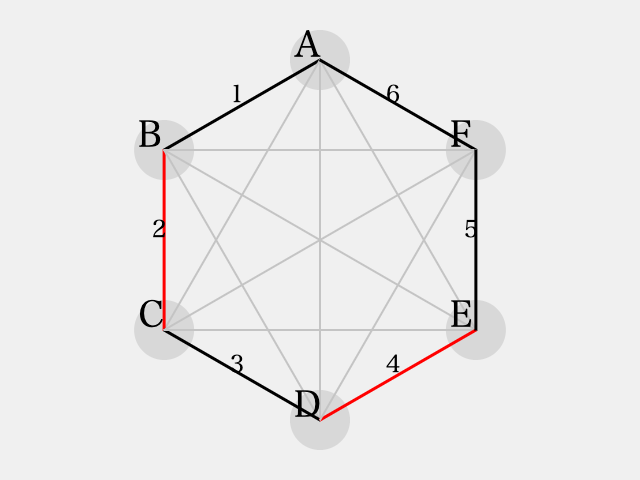
となり、これもまた のパターンとなり、同色三角形を避ける事ができない。
ゆえに、 として
のパターンのみ検討すれば十分であることがわかる。
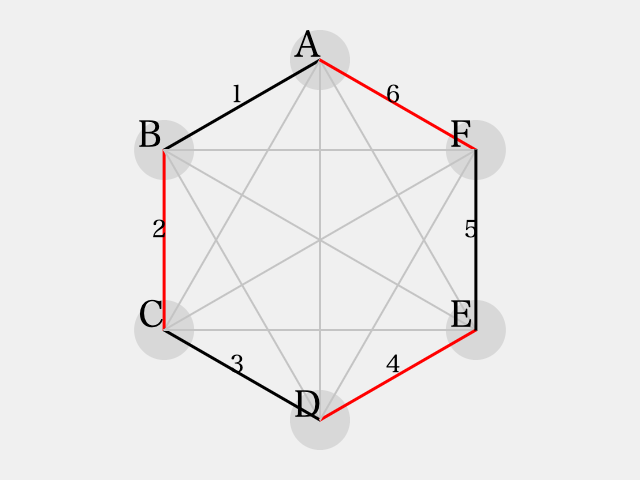
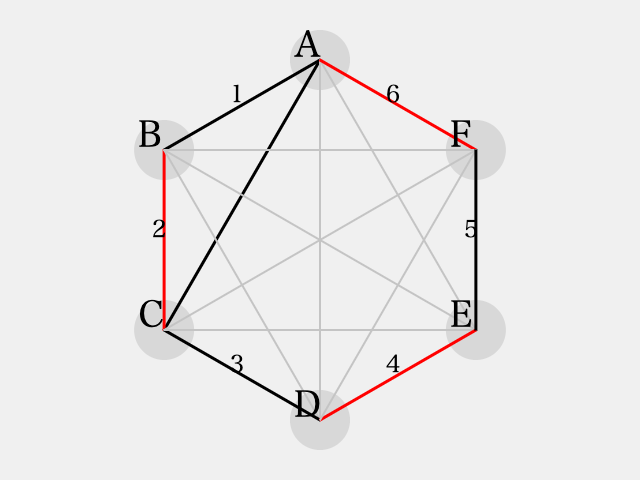
さて、ここで としても一般性は失わない。なぜならば、
としたものの色を反転し、
軸を中心に線対称の彩色パターンを考えると
をしたものに一致するからである。
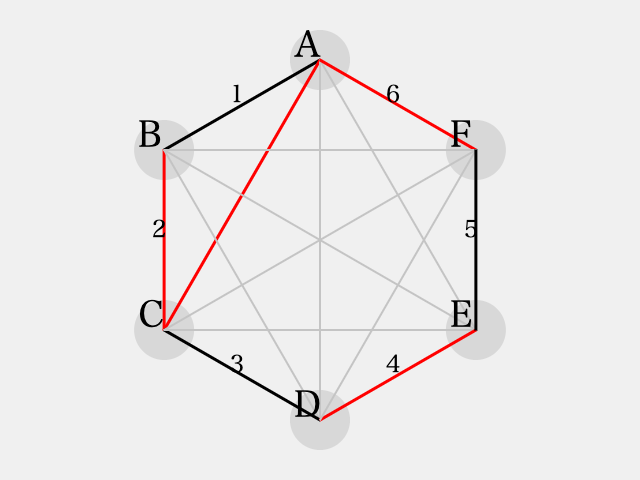
ここで、三角形 に着目すると
に彩色される。
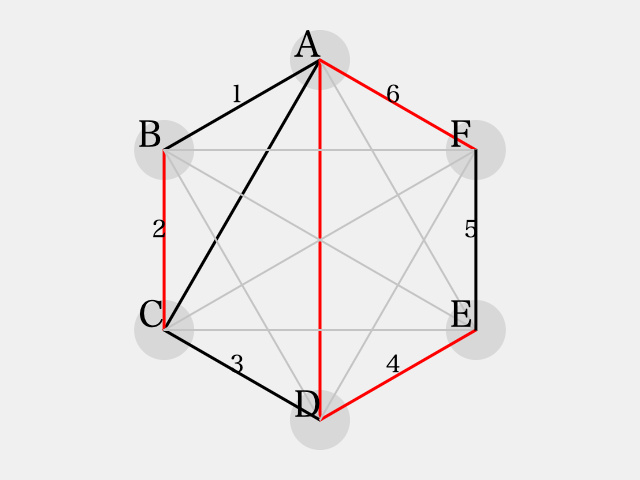
また、三角形 に着目すると
に彩色される。
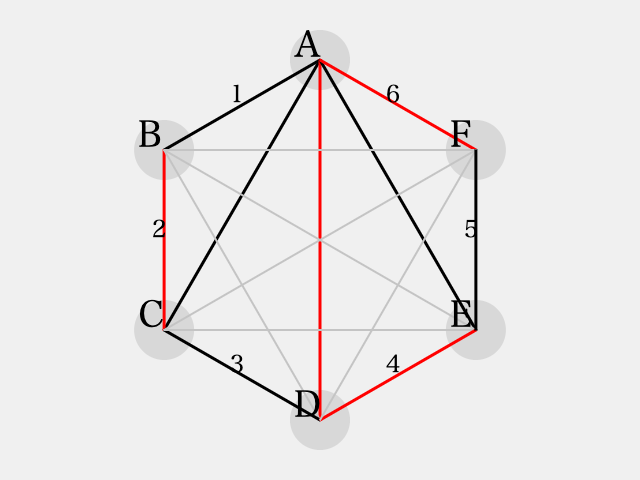
さらに、三角形 に着目すると
に彩色される。
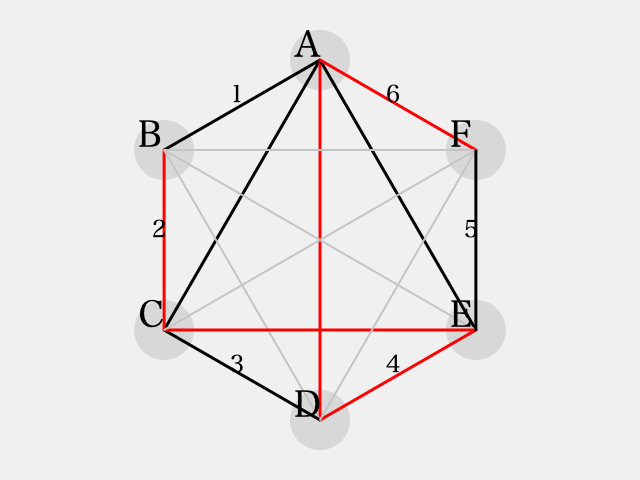
ここで、辺 に対していずれの色を彩色しても、同色三角形を避ける事ができない。
以上の議論により、 のパターンすべてに対して、同色三角形を避ける事ができないとわかった。
一方、 のパターンについては、これまでの議論を色を反転させて行えば良い。
したがって、頂点数 の完全グラフに対して、同色三角形を避けるような2色での彩色は不可能である事がわかった。
やったー!!証明できた!!!
私はこの解法で証明できることに気づいて、舞い上がって深夜の2時ごろにこんなツイートをしていました。
やったー!!!すごーく地味だけど、すべての組み合わせを調べ上げてN = 6のラムゼー問題が証明できた!面倒なので細かい証明は載せれてないけど、とにかくわかった。自力でできたのが嬉しい。 pic.twitter.com/iFCYurV6DR
— tsujimotter 日曜数学者 (@tsujimotter) 2020年7月2日
それぐらい嬉しかったのです。自分で証明できたのですから。
とにかく証明できてしまえば勝ちです。他にどんな洗練された証明があったとしても、泥臭い証明であっても、証明できてしまえば、証明は証明なんです。
3. 矛盾辺に着目した方法(解法2)
上で書いた方法は、私が自力で思い付いた嬉しい証明なのですが、ちょっと泥臭すぎますね。泥臭いだけではなく、このままでは頂点数17の場合に応用できません。もう少し証明を洗練させる方法はないでしょうか。
解法1を考えているうちに、次のような「矛盾辺」(と私が勝手に読んでいる)パターンが終了条件となっていることに気づきました。
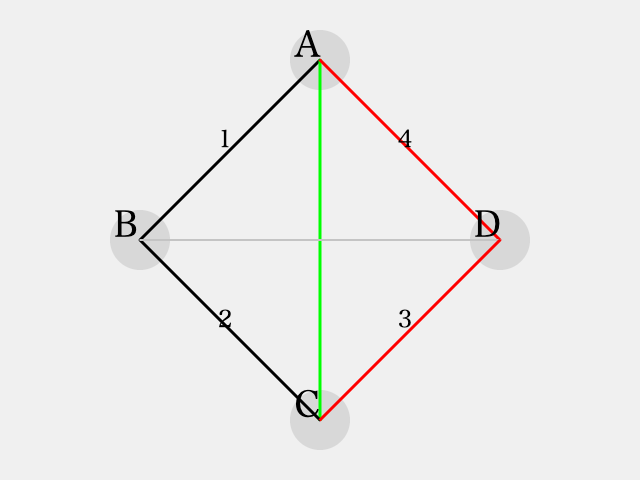
この図の辺 に対しては、
のいずれの色を塗ったとしても同色三角形ができてしまいます。このような辺を作ってしまえば、そのパターンでは同色三角形を避ける事ができないというわけですね。この矛盾辺パターンに着目して問題を解くことができないでしょうか。
それでは頂点数が少ないケースから順に分析してみたいと思います。
頂点数4のとき、本質的に下記の4通りしかないことがわかります。

「矛盾辺」のパターンを除けば、3パターンだけが2色で塗り分けられるパターンだというわけですね。
頂点数5のグラフは、頂点数4のグラフに1点追加したグラフとなっています。したがって、上記の塗り分けられる3パターンに1頂点追加した上で、塗り分けを検討すれば良いことになります。
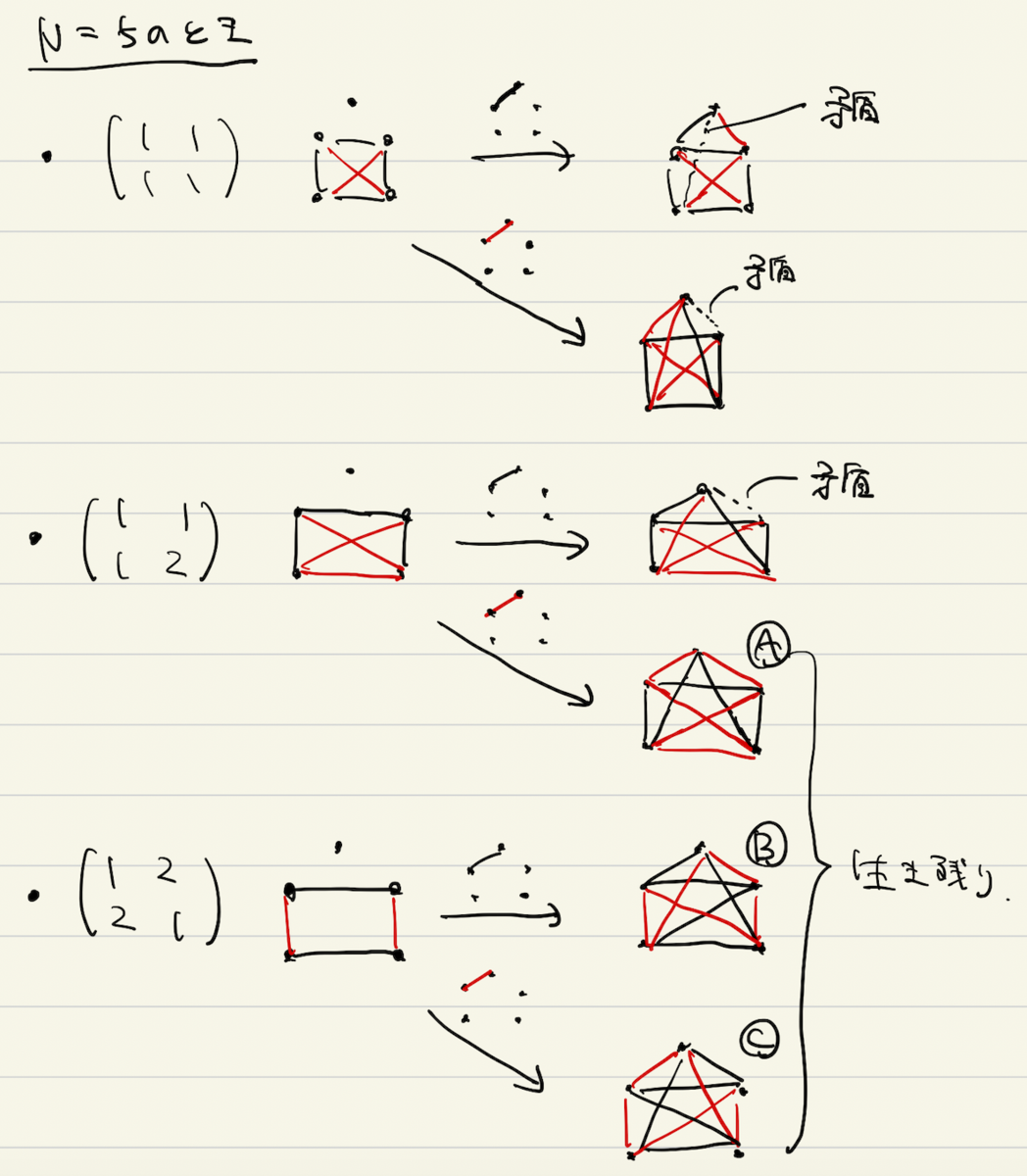
第1のパターンは、図の左上の辺を にするか
にするかのいずれかのパターンが発生しますが、実はどちらも彩色を進めると矛盾辺を導きます。
第2のパターンは、図の左上の辺を に彩色すると矛盾辺を導きます。したがって、
に彩色したパターンだけが生き残ります。これをパターンAとしましょう。
第3のパターンは、図の左上の辺を に彩色した場合と、
に彩色した場合と、いずれも生き残ります。それぞれパターンB・パターンCとします。
こんな風に頂点数5の塗り分けのパターンが、たった3通りしかない事がわかってしまいました。ということは、頂点数6の場合も、パターンA〜Cに対して1点加えたパターンだけ考えれば良いわけですね。
このまま頂点数6の証明に行けるでしょうか。
パターンAに対して、図の左下の辺を に彩色した場合と、
に彩色した場合でそれぞれ考えると、図のように矛盾辺を導きます。
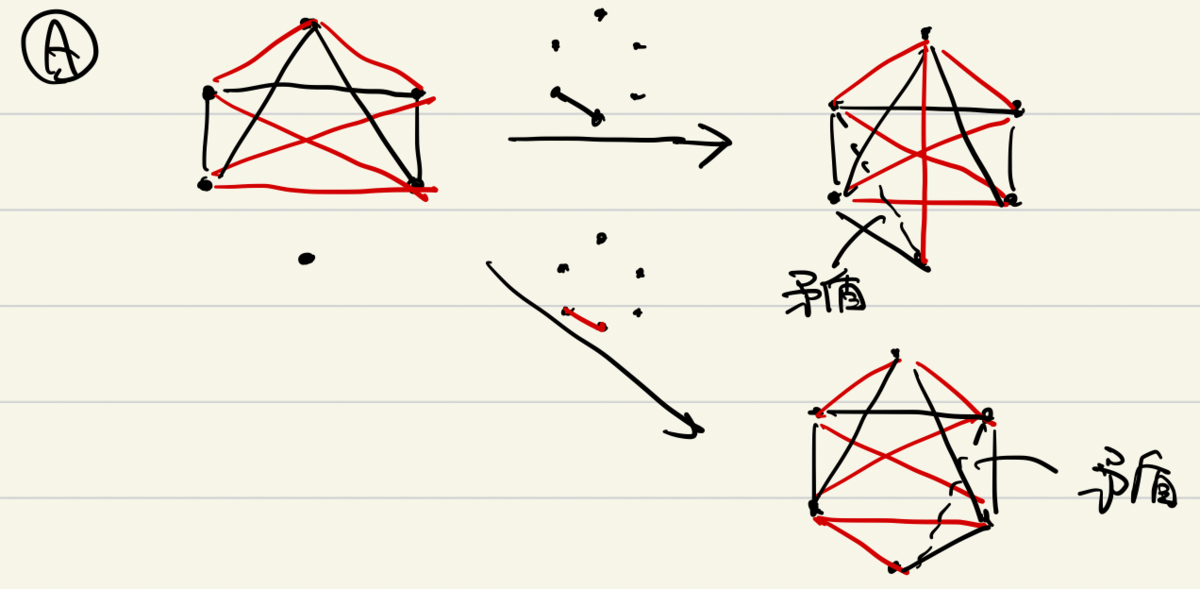
パターンBに対して、図の左下の辺を に彩色した場合と、
に彩色した場合でそれぞれ考えると、図のように矛盾辺を導きます。
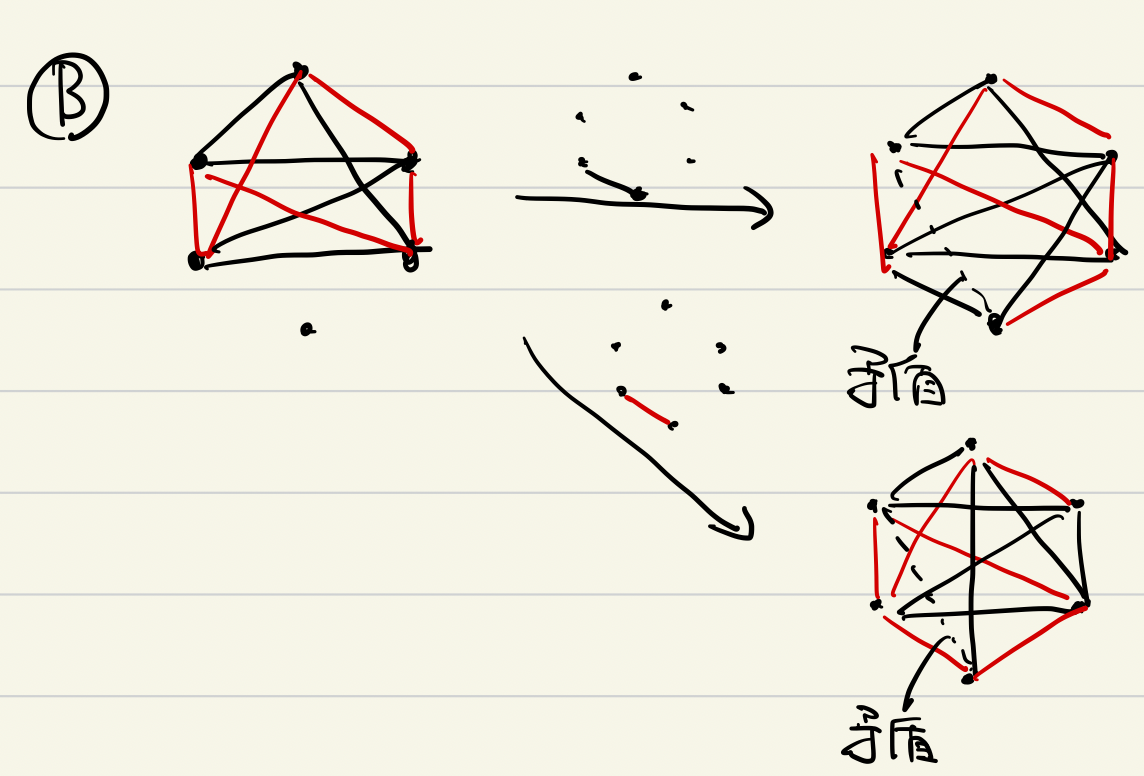
パターンCに対して、図の左下の辺を に彩色した場合と、
に彩色した場合でそれぞれ考えると、図のように矛盾辺を導きます。
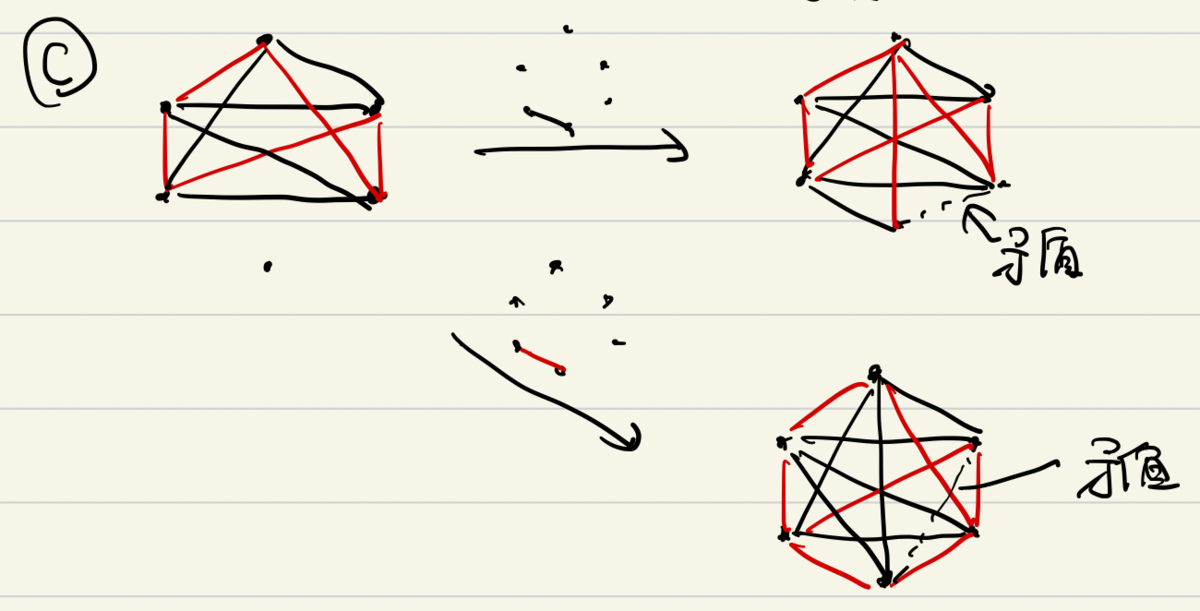
以上により、頂点数6のグラフに対して、同色三角形を避ける2色の彩色はできないことがわかりました。
4. より洗練された証明(解法3)と17頂点への一般化
解法2によって、ずいぶんとすっきりと証明ができましたね。もちろん、矛盾辺を導く過程は省略されているので、真面目にやろうとするともう少し議論が必要ですが。
しかしながら、この解法2の方法を頂点数17の場合に延長するのは、なかなか難しそうです。色も3色になり矛盾辺のパターンが増えてしまいますので、かなり大変そうです。
数学的帰納法のように、頂点数6・3色のケースに帰着して示すことはできないでしょうか?
そんなことを考えているうちに、ふと気づいたのです。
気づいたのはこんなアイデアです。
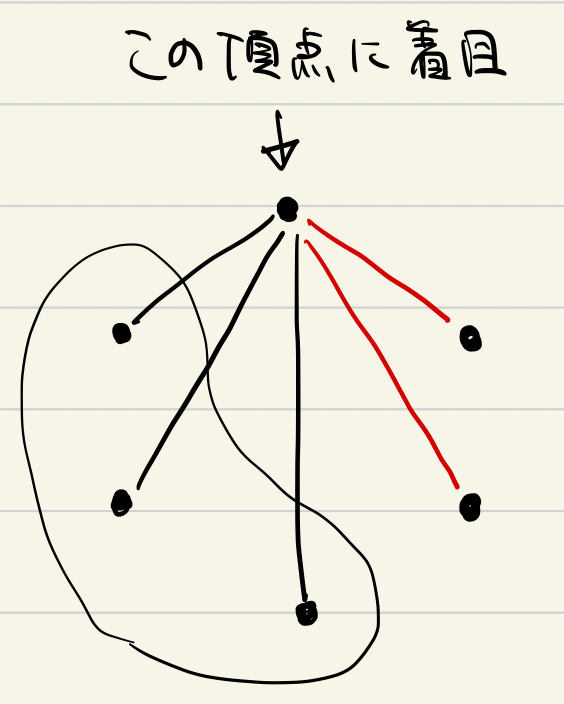
ある1点から3頂点に対して同じ色の線を引いてしまうと、その時点で同色三角形ができてしまう、ということです。
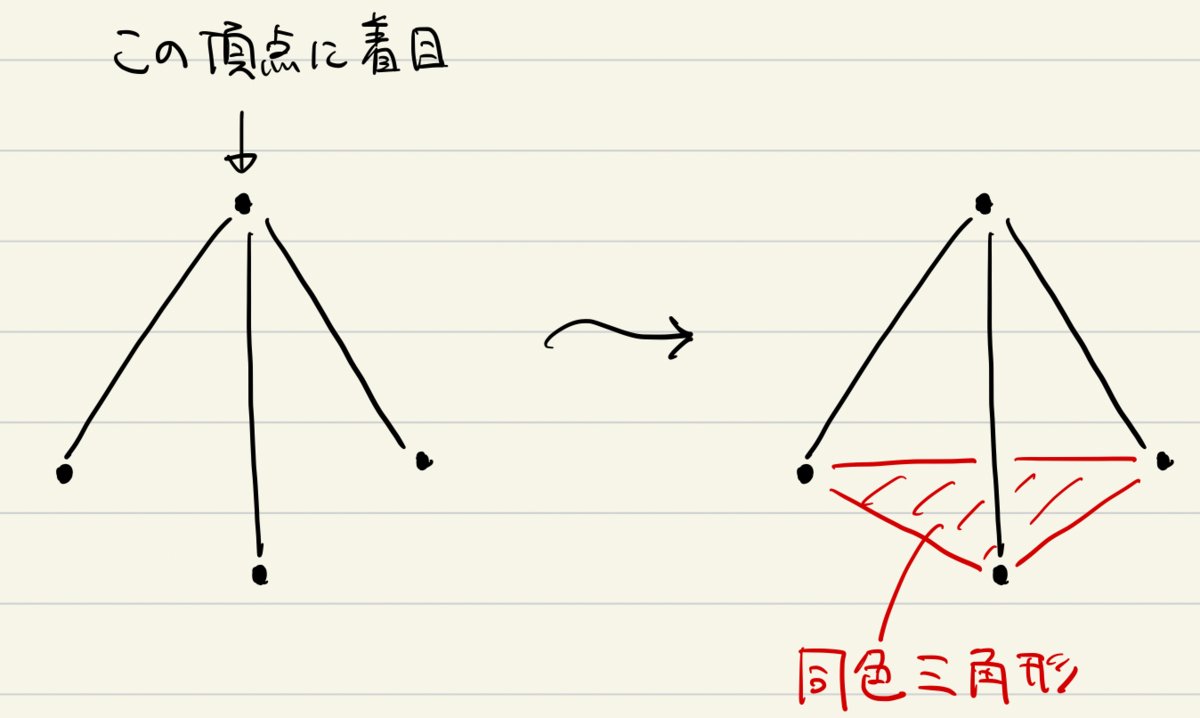
1点に着目してその点から出る辺の色に着目するというのが大きなブレイクスルーです。これで頂点数6の問題が一瞬にして解決してしまいます。
頂点数6のグラフの1点に着目します。このとき、その1点から残りの頂点に向かう辺は5本です。これらを2色に塗り分けるとなると、どちらかの色を少なくとも3本の辺に塗る必要が生じます。したがって、上の議論により、その色ではない色の同色三角形ができることになります。ゆえに、同色三角形を避ける彩色が不可能であることが示されました。
「えっ、これで終わり?」と驚くぐらい一瞬で証明できましたね。
この解法に気づいたとき天才だなと思いました。
実は、完全に独力でこの解法に至ったわけではありません。ラムゼー問題については、私一人ではなくパートナーと一緒に考えていました。これまでの解法1と解法2は完全に私の独力ですが、「1点に着目する」というアイデアはそのパートナーのものです。しかしながら、それでもほとんど何も参考にせずに解法に到れたというのは私にとって感動的な出来事でした。
この解法を進めていくと、実は 元々の頂点数17の問題(定理1)も解くことができます 。この解法も解法3のあと自力で思いついたものですが、最後に紹介しましょう。
頂点数17のグラフのうち1点に着目します。すると、残りの頂点に向かって16本の辺が伸びています。
これら16本を3色で彩色することを考えると、3色中1色は少なくとも6本の辺に塗られることになります。
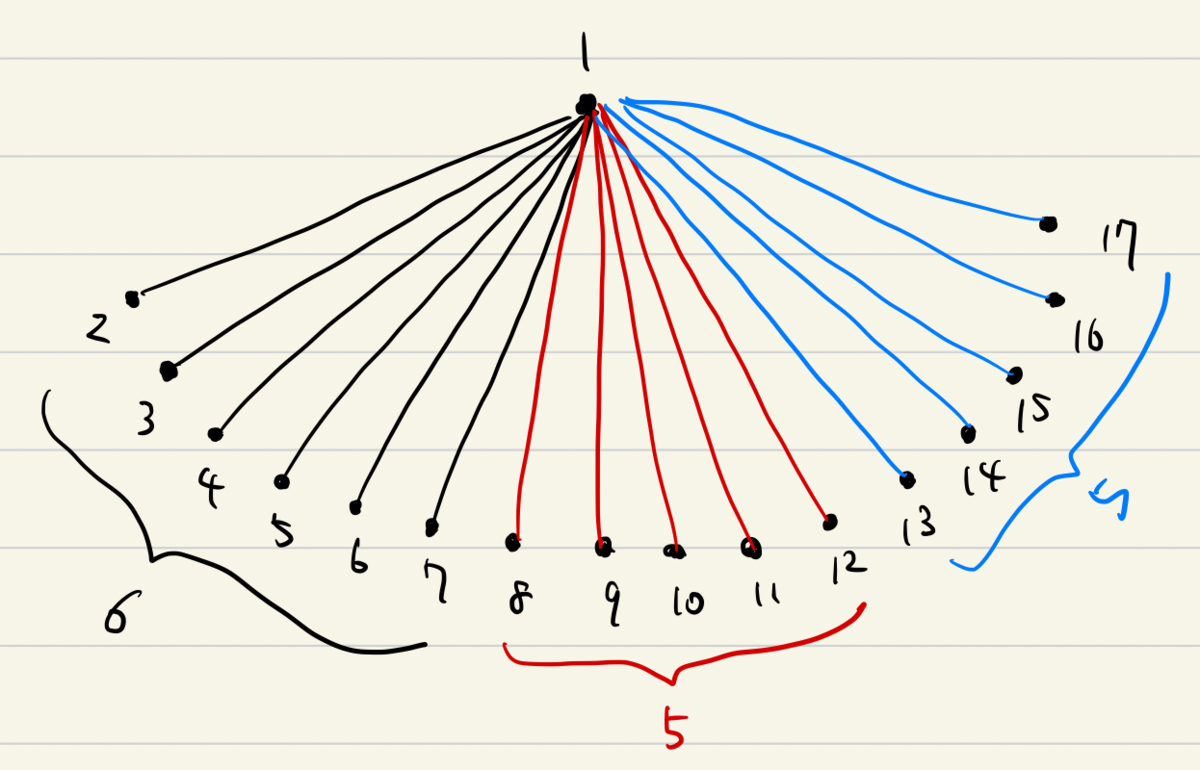
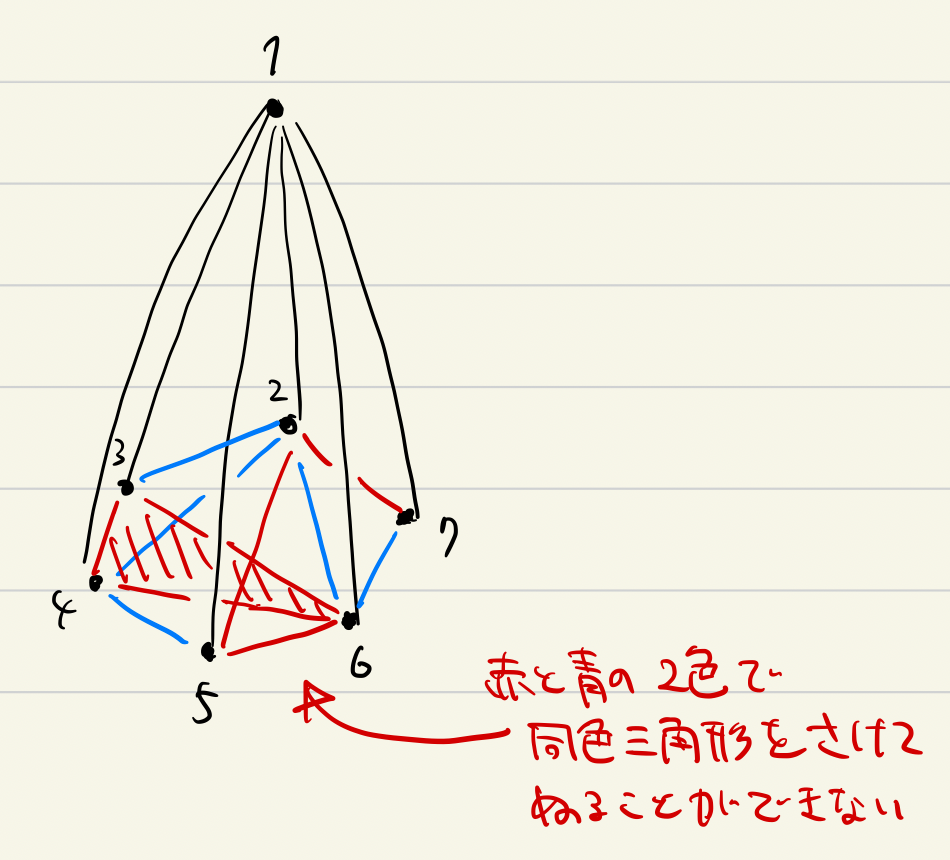
この6個の頂点の間をつなぐ辺には、その6頂点に向かう辺に塗られた1色は塗ることができません。したがって、この6頂点の間の辺は残り2色で塗る必要があります。
一方で、6頂点は2色で塗ることはできませんでしたから、頂点数17のグラフを同色三角形を避けて3色で塗ることはできないことが示されました。
これにて数学ゴールデンの問題は解決です!!
5. ラムゼーゲーム(tsujimotterからの出題)
ここまで読んでくださった皆様に、せっかくなので追加の問題を出題してみたいと思います。上記の解法を知っていた方も、ぜひチャレンジしてみてください。
これまでの証明で明らかになったように、頂点数6の完全グラフは2色で、頂点数17の完全グラフは3色で(同色三角形を作らずに)塗ることができないのでした。同様の方法で「頂点数66の完全グラフは4色で塗れない」ことが証明できます。
逆に、これ以外の頂点数の完全グラフを塗ることができるでしょうか? 実際、先ほどの証明では頂点数 16 までの完全グラフが3色で塗れるかどうかについては、何も言及していません。
実は、頂点数 16 までの完全グラフは、すべて同色三角形を避けて3色で塗ることができます。面白いですね!
そこで、みなさんにチャレンジしていただきたいのは、頂点数 7 〜 16 について同色三角形を避けた彩色パターンを見つけることです。第1節で紹介したアプリを使って塗り方を見つけてみてください。これが ラムゼーゲーム です。
tsujimotter.info
また、頂点数 17 〜 65 についても、同色三角形を避けた彩色パターンを考えてみてください。
実は、これには 未解決問題 を含んでいます。どうやら、Wikipedia「ラムゼーの定理」によると、頂点数 51 〜 62 については、同色三角形を避けた彩色パターンがあるかどうかわかっていない(証明されていない)ようなのです。
こんなところに未解決問題があるなんて、面白いですね!
6. まとめ
今日は、数学ゴールデンに出てきた「ラムゼーの定理」に関する問題について、私が解いた過程を紹介しました。
最初の解法では、本当に泥臭く、辺の彩色のすべてのパターンをしらみつぶしに調べる形で証明しました。そんな方法でも、粘り強くトライすれば証明できることがわかって、深夜にも関わらず本当に興奮しました。
2つめの解法としてより簡潔な方法を見つけ、最終的には1点から出る辺に着目することで、洗練された証明を得ることができました。この方法を延長させることにより、元々の問題も解決することができました。
数学ゴールデンの元々の問題は数学オリンピックで出題された有名問題でもあるので、既に解法を知っている方が多いのかもしれません。私は解法を知らなかったわけですが、逆にそれがよかったとも思っています。こんなに楽しむことができて、自分で問題を解く楽しさを味わうことができたからです。日曜数学の楽しみ方が一つ増えて嬉しいです。
数学ゴールデンの問題はこの問題の他にもまだまだあります。実は、数学ゴールデンで「問題を解くまで次のページに進まない」という試みは まだ続けています 。そして、2020年12月現在「近藤宏樹さん作成のチャレンジ問題」を解いている最中です。つまり、まだ解けていません。笑
この問題が自力で解けるものなのかどうかは正直わかりませんが、まだまだ楽しめそうです。自分で問題を解く楽しさを教えてくれた(そういう趣旨の漫画ではないけど)数学ゴールデンに感謝です。
最後まで読んでいただいてありがとうございました!
冒頭にも書きましたが、日曜数学アドベントカレンダーに投稿してくださった皆様に、改めて感謝申し上げます。どの記事も、本当に気合の入った記事を書いてくださって、毎日記事が公開されるのが楽しみでした。
まだ読んでいないという方は、ぜひ読んでみてください!
adventar.org
それでは、2021年も楽しく日曜数学していきましょう!
*1:Math Power 2017の関真一朗さんによる講演で「Ramsey理論」の一例として紹介されています。動画はこちら: www.nicovideo.jp
