tsujimotterのノートブック

日曜数学者 tsujimotter の「趣味で数学」実践ノート

箸袋で作った図形は正五角形か？

数学日曜数学幾何学折り紙

今日は箸袋があるとつい作っちゃうこの図形についての話です。

f:id:tsujimotter:20210328012856j:plain:w400

細長い紙を用意して、上の図をイメージしながら折り曲げて「ぎゅっと」すると、きれいに正五角形が作れてしまいます。

箸袋に限らず、お手元に紙テープなど「細長い帯状のもの」があれば簡単に折ることができます。よかったらぜひやってみてください。

ところで、上で作った図形はたしかに五角形ですが、本当に正五角形だろうか？というのが本日の問いです。つまり、辺の長さと角の大きさは、厳密にすべて等しいのでしょうか？

これまで漠然と正五角形だろうと思っていましたが、よくよく思い返してみると、それを証明したことはありませんでした。一見簡単にできそうな気がしたのですが、やってみたらなかなかチャレンジしがいのある問題でした。

というわけで、今日は「箸袋で作った図形が正五角形であること」を証明してみたいと思います！

tsujimotterは昨日の夜にこの問題について考えていたのですが、証明が完成できたときはとても爽快な気持ちになりました。この快感を味わってもらいたいので、お時間ある方は、ぜひ一度自分で証明を考えてみてください。

以下では、私の思いついた証明方法を紹介したいと思います！

図示してみよう

まずは状況を図示してみましょう。

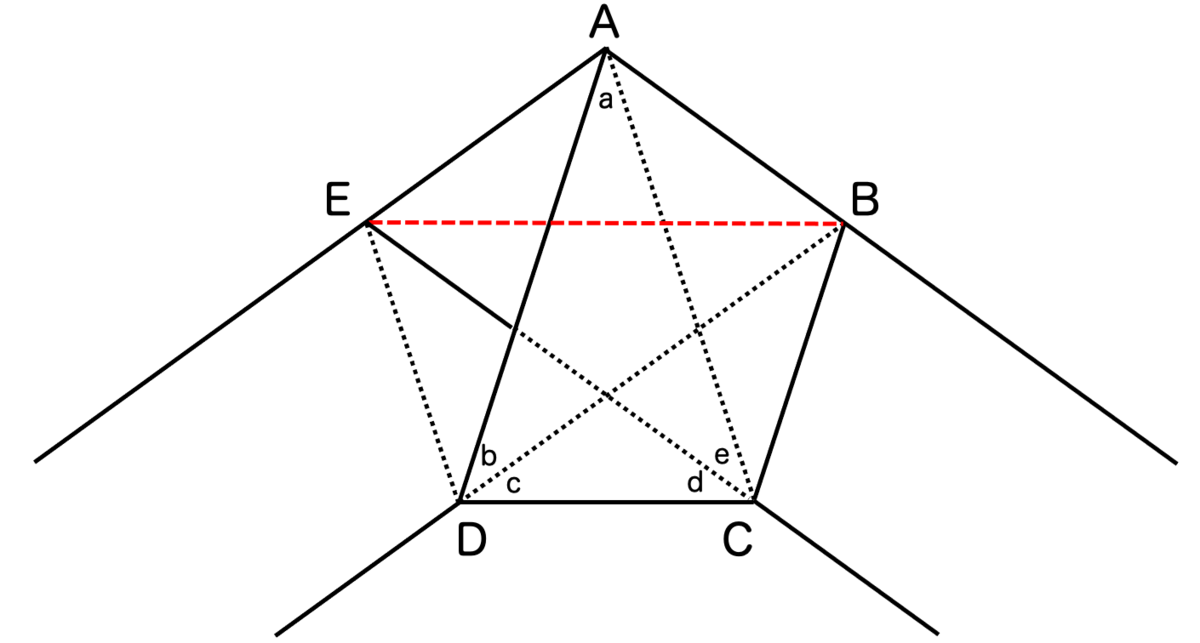
f:id:tsujimotter:20210328022950p:plain:w360

あとで説明しやすいように、五角形の各頂点を折り目をつける順にA, B, C, D, Eとし、未知の角度を図のように $a, b, c, d, e$ と振っておきます。

注意したいのは、赤色で書いた線分BEについては、実際には帯が通っていないということです。つまり、最後にもう一度折り返したときに、赤い線の部分を帯の一辺が通るとは限らないというわけですね。一見、対称性があるようで、対称性がないのです。
（結果的には正五角形であることが示されれば、折り返したときに帯の境界部分が赤い線を通ることが保証できます。）

実はこの直線BEが、五角形の底辺の線分CDと平行であることが示せます。これが示せると途端に対称性が上がって、情報量が増えることになります。

証明に使える道具

今回の問題を考える上で、使えそうな道具について考えてみましょう。

道具1. 帯は平行線

一つ目の道具は、帯の境界の2辺は平行線であるという点です。

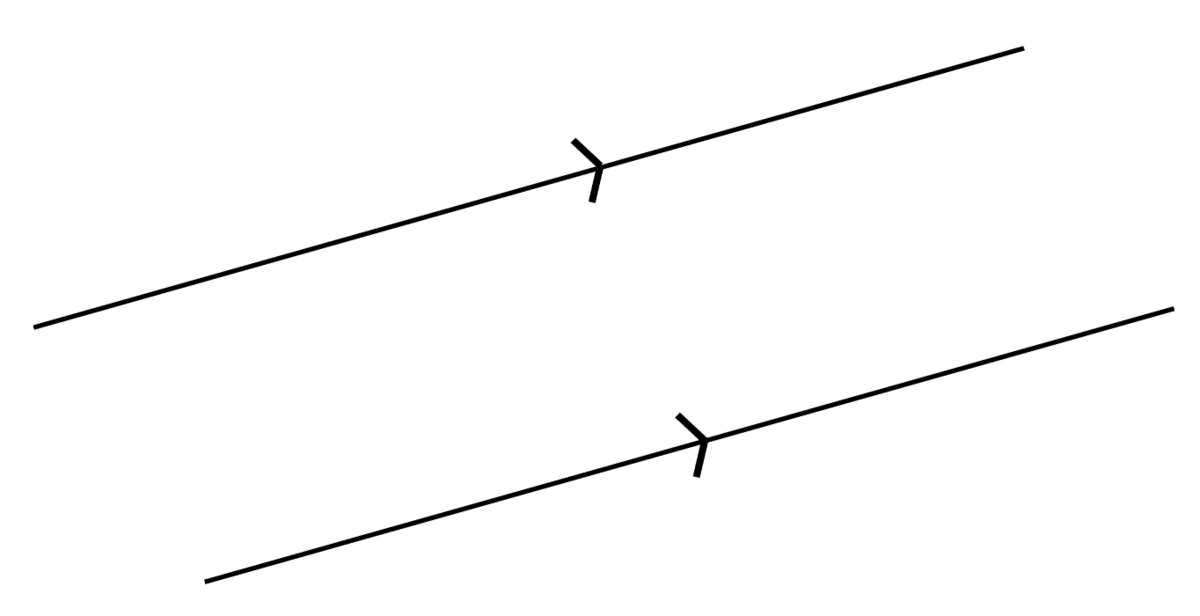
f:id:tsujimotter:20210328023244p:plain:w300

これによって平行線が至るところに現れます。平行線があれば、錯角や同位角によって、いろんな角が等しいことが示せるわけですね。

道具2. 折り返しの定理

次の図のように折り返して得られる角 $a, b$ を考えると、 $a + 2b = 180^\circ$ が成り立ちます。

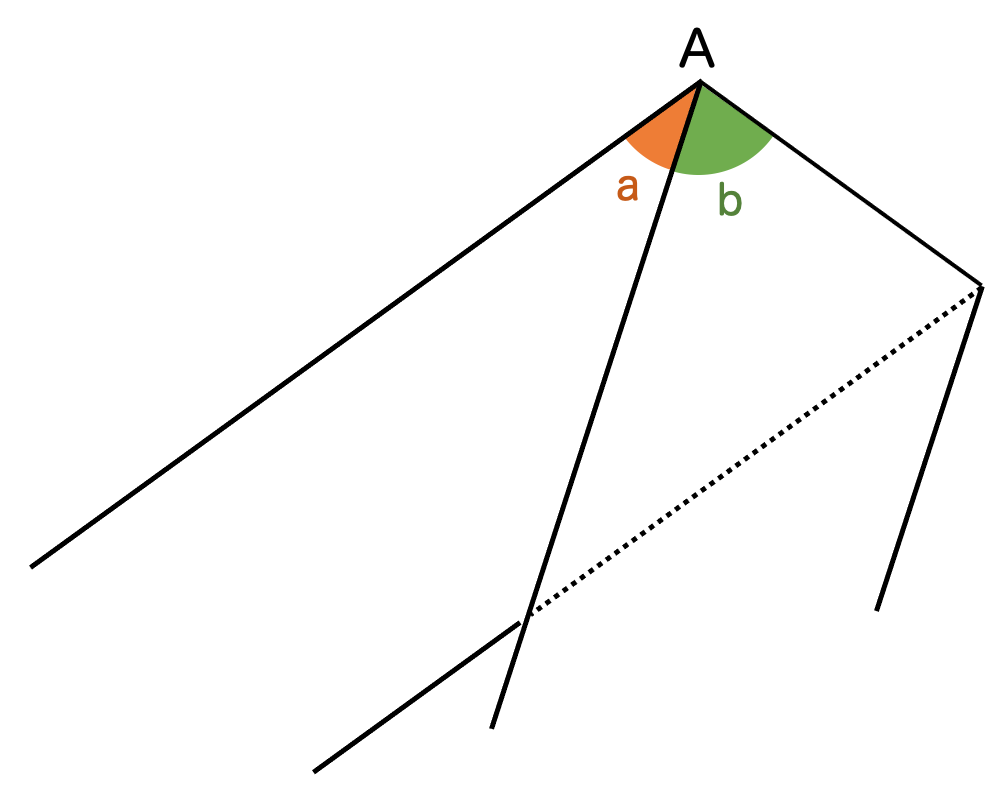
f:id:tsujimotter:20210328023316p:plain:w300

これは折り返した部分を開くとわかります：

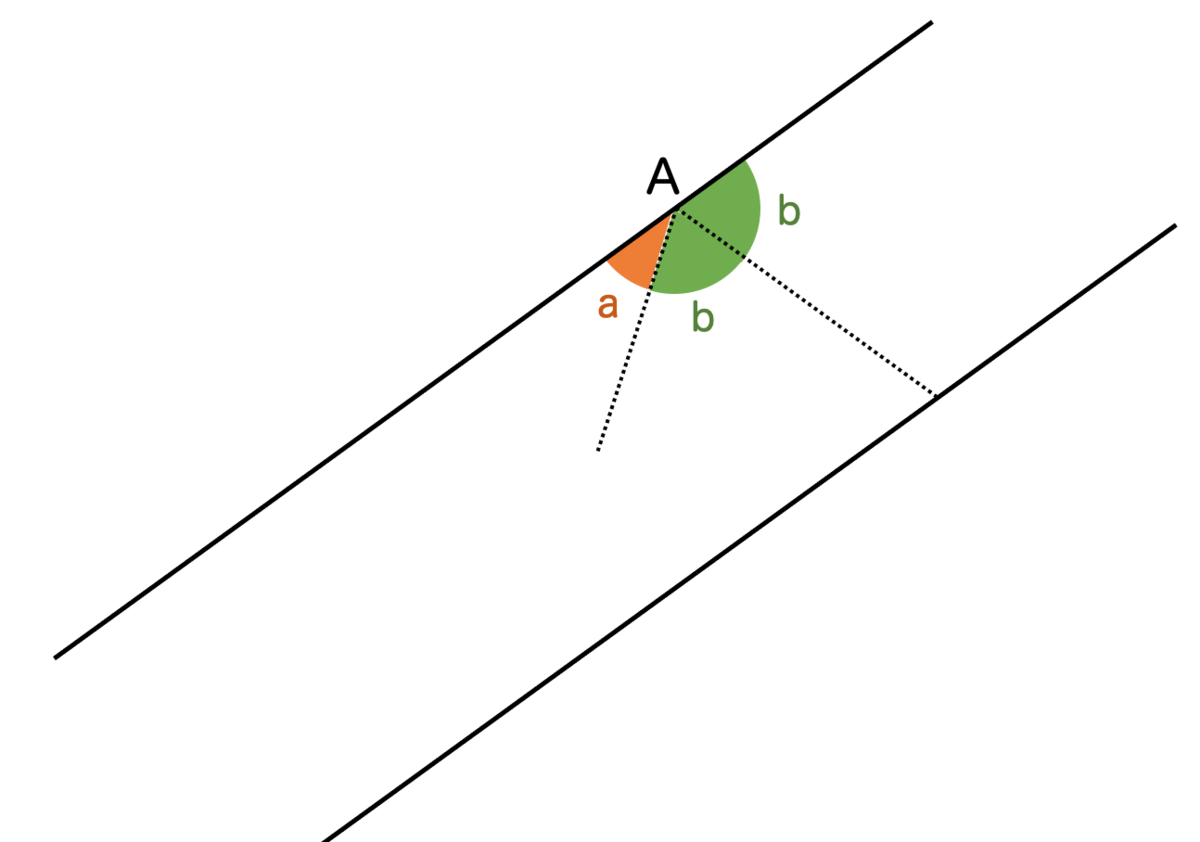
f:id:tsujimotter:20210328023336p:plain:w300

直線のなす角は $180^\circ$ というわけですね。

これは私が勝手に名付けた定理ですが、折り紙ならではの性質かなと思います。面白いですね。

２つの道具を紹介しましたが、逆に言えば、この２つぐらいしか拠り所がなさそう（他にもあるかもしれませんが）というのがこの問題の難しさでもあります。

三角形ACDが二等辺三角形であることの証明

それでは証明に移りましょう。青く囲った三角形ACDが二等辺三角形であることを示します。

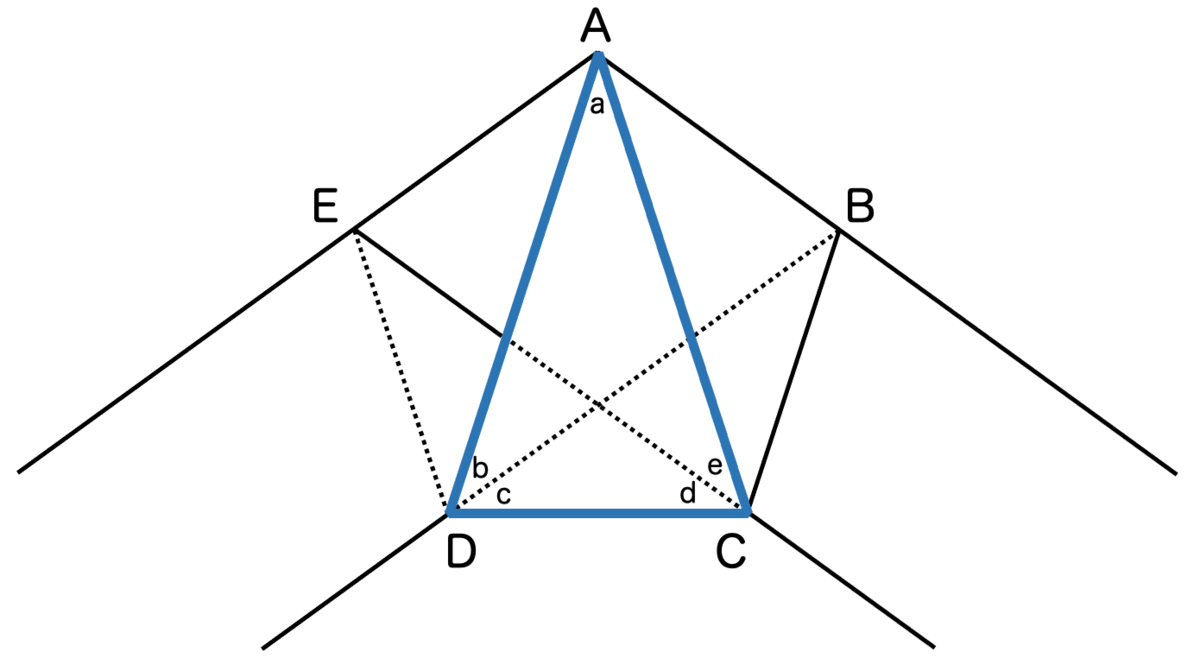
f:id:tsujimotter:20210328023433p:plain:w330

平行の錯角を使って、角度が $a, b, c$ に等しい角を見つけることができます。

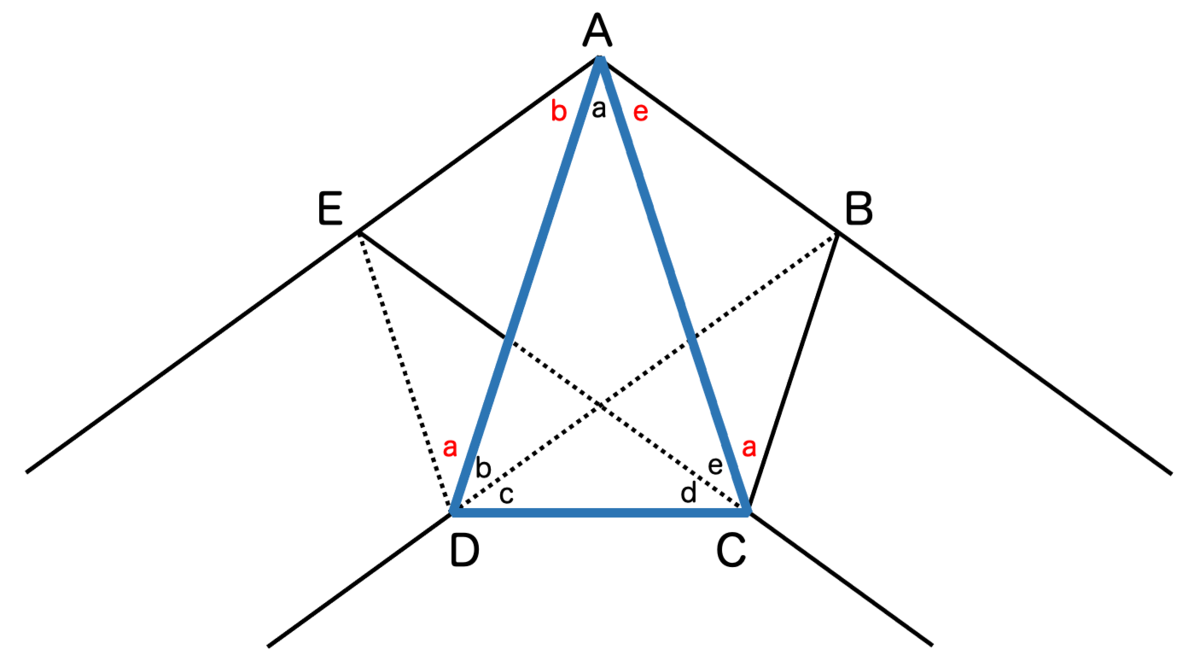
f:id:tsujimotter:20210328023451p:plain:w330

これで頂点A, C, Dの内角はそれぞれ $b+a+e, \; a+e+d, \; c+b+d$ となります。

ここで、頂点Cの部分で一回折り返していることから、折り返しの定理が使えます。

$a+2(d+e) = 180^\circ \tag{1}$

また、三角形ACDの内角の和が180°であることから

$a+b+c+d+e = 180^\circ \tag{2}$

が成り立ちます。

式 $(1)$ から式 $(2)$ を引くと

$b+c = d+e \tag{3}$

が得られます。

これで三角形ACDが二等辺三角形であることが言えました。

ついでなので、もう少し示しておきます。頂点Aを観察すると、そのまわりで２回折り返しをしていることがわかります。よって、折り返しの定理を２回適用すると、次の２式が得られます。

$b+2(a+e) = 180^\circ \tag{4}$

$e+2(a+b) = 180^\circ \tag{5}$

式 $(4)$ から式 $(5)$ を引くと

$b = e \tag{6}$

が得られます。

よって、式 $(3)$ と合わせて

$c = d \tag{7}$

も得られます。

結局、出てくる角度はすべて左右対称だったということですね！

線分BEと線分CDが平行であることの証明

続いて、線分BEと線分CDが平行であることを示します。証明のキーとなるパートですね。

次の図では、これまで示した $d = b, \; e = c$ を使って、角度の変数を $a, b, c$ の３つに絞りました。

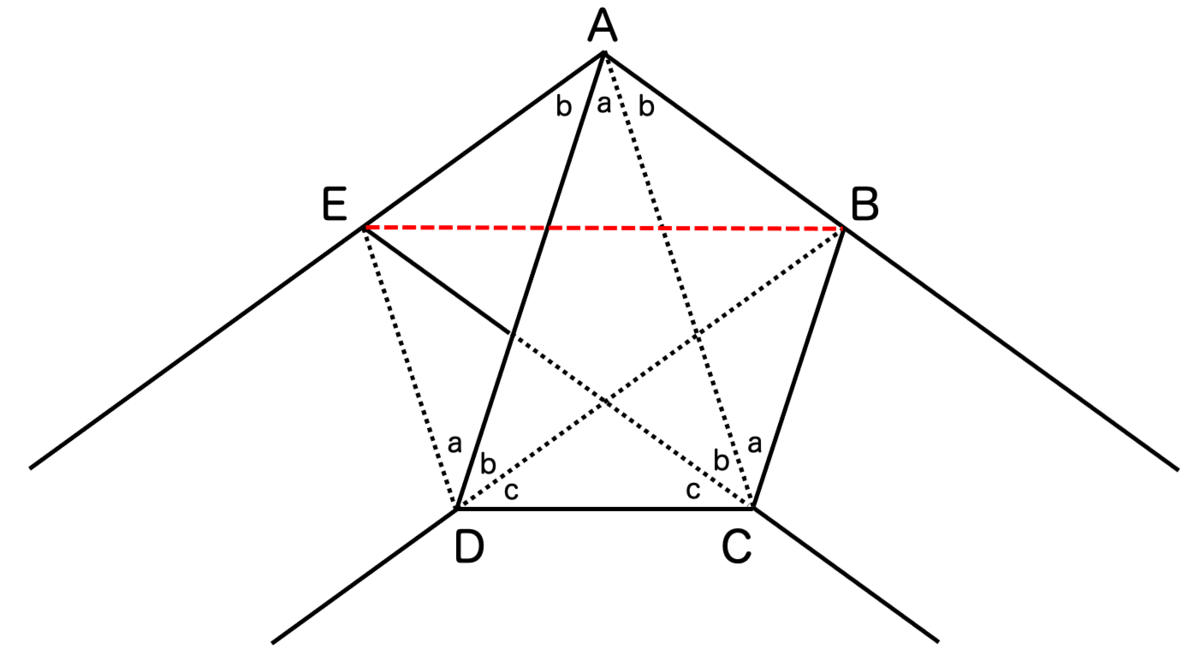
f:id:tsujimotter:20210328023517p:plain:w330

図のような補助線を引きます。

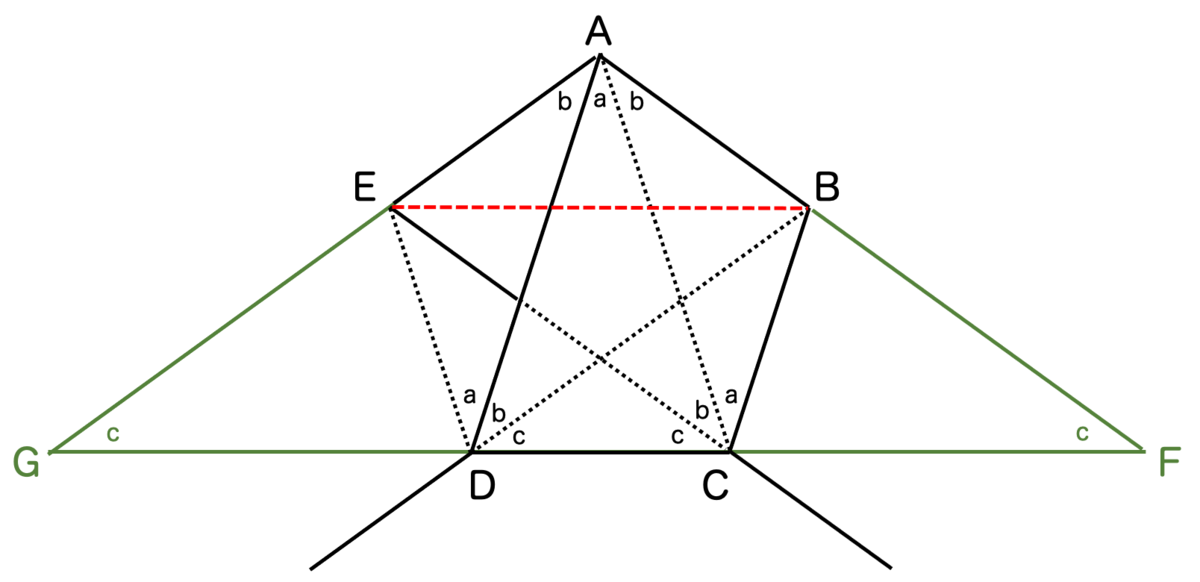
f:id:tsujimotter:20210328023606p:plain:w330

線分ABを延長させた直線と線分DCを延長させた直線の交点をFとし、同様に線分AEを延長させた直線と線分CDを延長させた直線の交点をGとしているわけですね。

平行線の同位角から角Fと角Gが $c$ であることがわかります。したがって、一番大きな三角形AFGは二等辺三角形であることがわかります。

よって、１つの頂点とその頂点を通る対称軸を共にする二等辺三角形ACD, AFGが得られたわけですね。

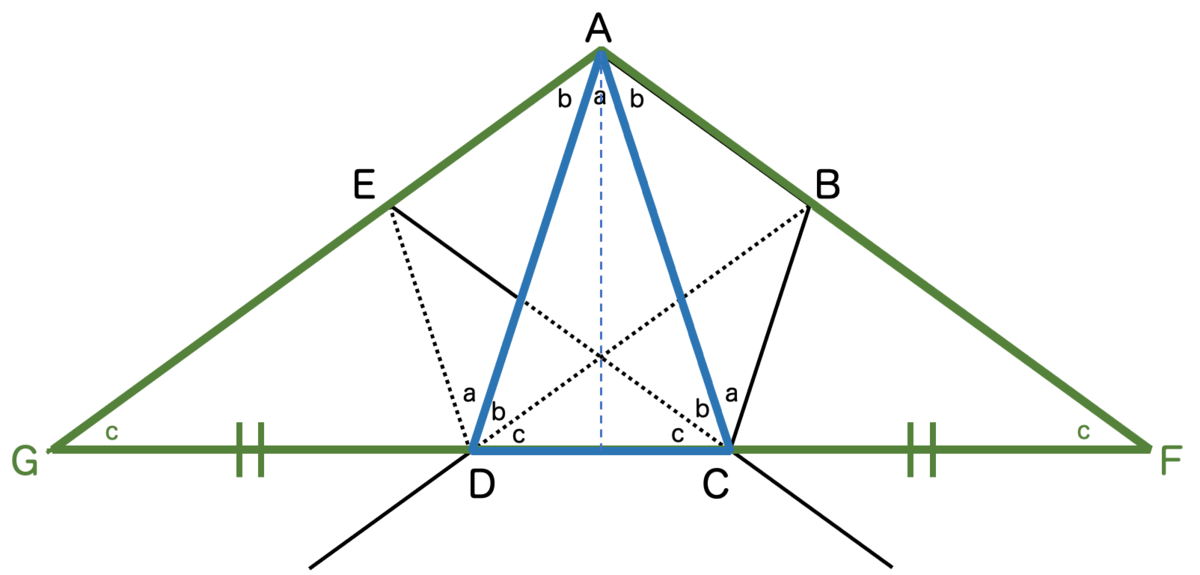
f:id:tsujimotter:20210328023654p:plain:w330

これにより、辺CFと辺DGの長さが等しいことがわかります。

また、角BCFと角EDGも等しいので、１辺とその両端の角が等しいことから、三角形BCDと三角形EDGは合同であることが言えます。ゆえに $BC = ED$ がわかります。

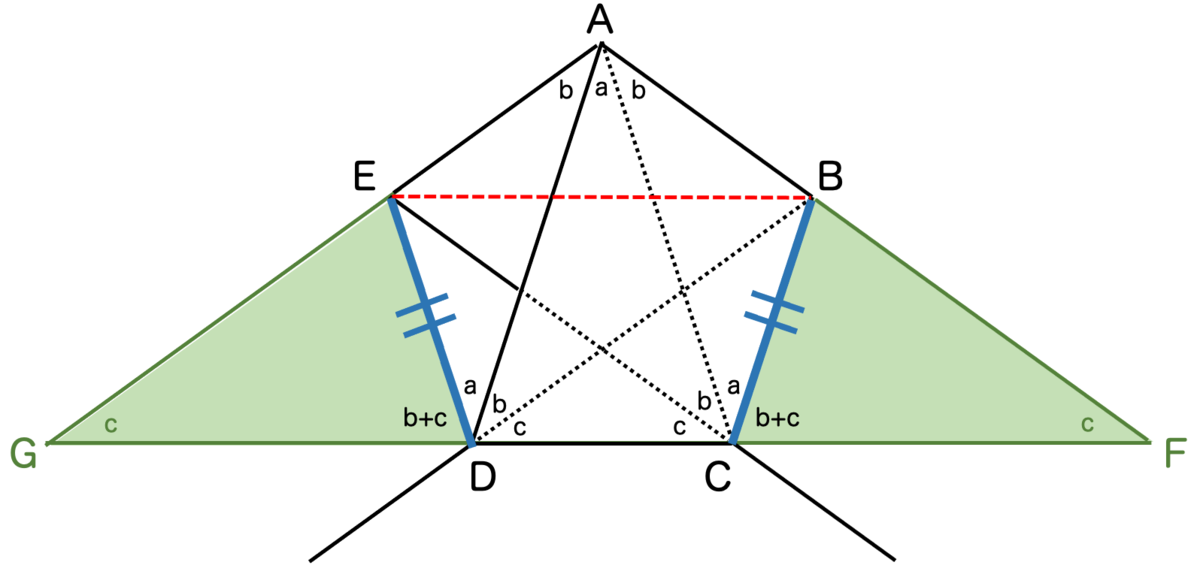
f:id:tsujimotter:20210328030408p:plain:w330

頂点Cと頂点Dの内角が等しく、かつ、辺CBと辺DEが等しいので、四角形BCDEは等脚台形になります。したがって、辺BEと辺CDは平行であることが示されました。

正五角形であることの証明

BEとCDが平行であることが言えたので、錯角と同位角を使って次のように角度が決まります。

f:id:tsujimotter:20210328023843p:plain:w330

あとは、①正五角形のすべての辺の長さが等しいことと、② $a = b = c$ が言えれば証明完了です。

頂点Aに折り返しの定理を使うと

$a + 2b + (a+b) = 180^\circ \tag{8}$

となります。また、三角形ACDの内角の和より

$a + 2b + 2c = 180^\circ \tag{9}$

となりますので、式 $(8)$ と式 $(9)$ の差をとって

$a + b = 2c \tag{10}$

が得られます。

これにより、頂点Aの内角は $b+a+b = b+c+c$ となり頂点Bの内角と一致します。ABとECは平行なので、四角形CBAEは等脚台形です。ゆえに、 $BC = AE$ が言えます。

同様に、頂点Aの内角と頂点Eの内角が等しいので、四角形BAEDも等脚台形です。ゆえに、 $AB = ED$ も言えます。

四角形BCDEも等脚台形なので、これで正五角形の５辺のうち、４辺の長さが等しいことがわかりました。

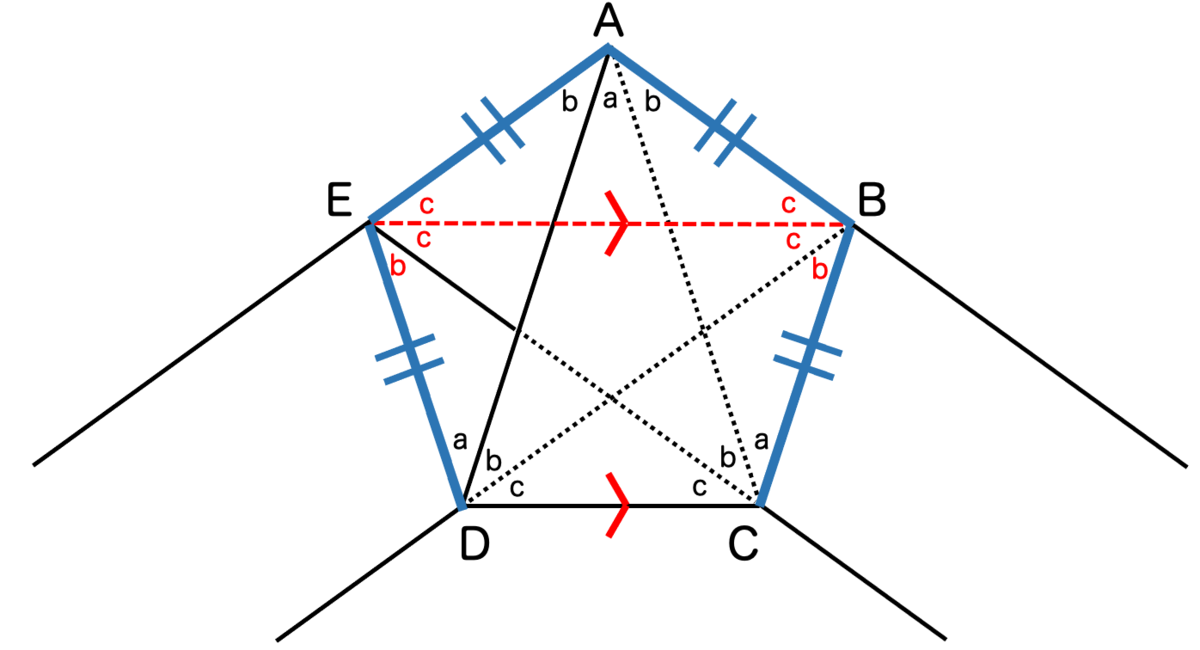
f:id:tsujimotter:20210328023933p:plain:w330

三角形EADに着目すると、辺EAと辺EDの長さは等しいので二等辺三角形です。よって、 $a = b$ がわかります。これを $a+b=2c$ に代入すると、 $b = c$ もわかります。

以上により、 $a=b=c$ がわかり、五角形のすべての角が等しいことが言えました。

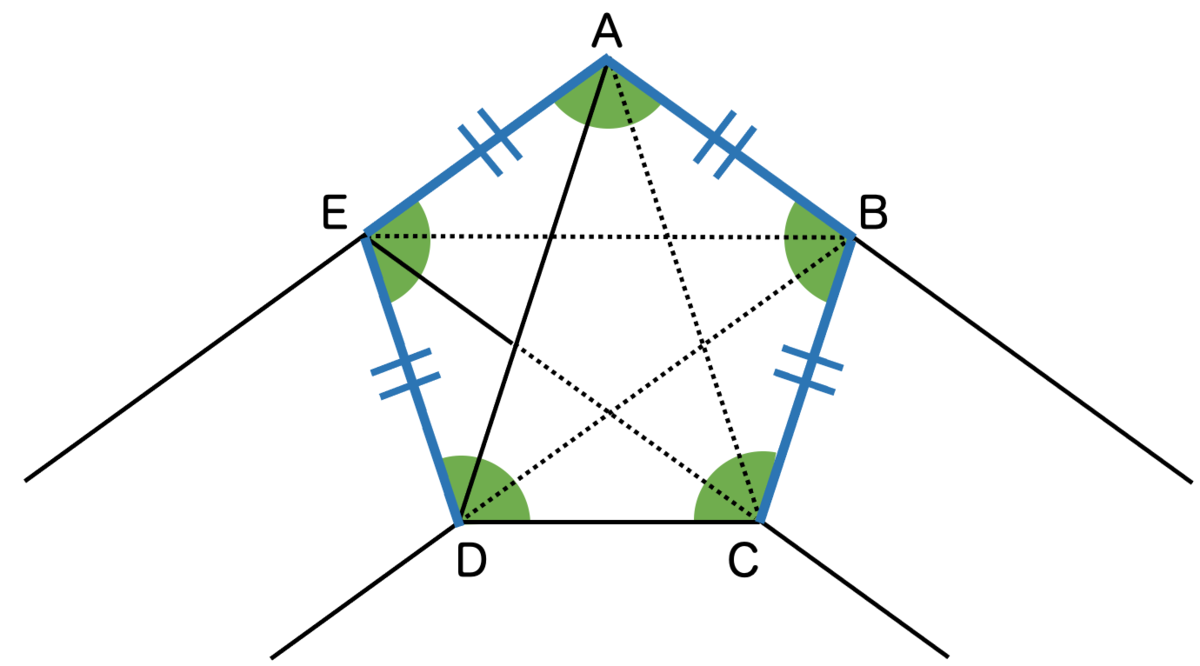
f:id:tsujimotter:20210328024002p:plain:w330

最後に、四角形ABCDに着目すると、やはり等脚台形なので、五角形のすべての辺の長さが等しいことが言えました。

以上により、五角形ABCDEは正五角形であることが示されました。

（証明おわり）

おわりに

というわけで、箸袋で作った図形で正五角形であることが示されました。これで自信を持って「正五角形だ」と言い切れるようになりましたね！

もっとスマートな方法はあるかもしれません。しかしながら、こういうのはどんな泥臭い方法であっても、自分で証明できたという事実が大事だったりします。

証明に至るまでには結構悩んだのですが、それもまた楽しかったです。こういうのが日曜数学の醍醐味ですね。

それでは今日はこの辺で！

参考文献

まだ手に入れていないのですが、今日の図形の折り方は下記の本に載っているそうです。

折る幾何学約60のちょっと変わった折り紙

折る幾何学約60のちょっと変わった折り紙

作者:前川淳
発売日: 2016/09/13
メディア: 単行本

追記

一通り自分で考えてみてから調べてみたところ、もっとスマートな証明がありそうです。メモとしてリンクを記載しておきます；

坂口杲一「紙テープを結んで出来る多角形について」奈良教育大学教育研究所紀要
https://nara-edu.repo.nii.ac.jp/?action=repository_action_common_download&item_id=9749&item_no=1&attribute_id=17&file_no=1
（リンクをクリックすると、記事のPDFファイルが直接ダウンロードされるので注意）