保型形式（モジュラー形式）を勉強するとこんなにも楽しい（応用編）

今回は「保型形式（モジュラー形式）を勉強するとこんなにも楽しい」シリーズの応用編です！

数学ガール等を読んで保型形式について知ったけど、さわりの部分だけでは物足りない、もっと保型形式のその先を勉強してみたい、そう思っていた「あなた」のためのシリーズ記事です。

前回の記事では、「導入編」と称してモジュラー形式に関する最低限の事項を紹介しました。導入編で手に入れた知識は、まさに今回の応用編を読むために用意したものです。
tsujimotter.hatenablog.com

今回は「モジュラー形式を勉強するとこんなにも楽しい」ということを紹介したいと思います。いよいよ本題ですね。

前回の記事を読んだ方もそうでない方も、必要に応じて前回の記事を参照しつつ、読んでいただけたらと思います。

みなさんにご紹介したいのは、次の５つの話です。

応用①：「関数」の間の非自明な関係式が得られる（難易度：★★）
応用②：「数列」の間の非自明な関係式が得られる（難易度：★★）
応用③：ヘッケ作用素と2次のゼータ（難易度：★★★）
応用④：素数を表現する2次形式（難易度：★★★★★）
応用⑤：楕円曲線とフェルマーの最終定理（難易度：★★★★）

もちろんここにあげていないようなおもしろい話は、他にもたくさんあるかと思いますが、そういう話はまた別の本で読むときの楽しみにしてください。今回選んだ５つのテーマは、私が保型形式（モジュラー形式）を勉強する中で、本当に感動したものだけを厳選して集めたものになっています。

中には相当難しい話も混ざっていますが、必ずしも全部理解できなくても大丈夫です。新しい世界のピクニックだと思って「散策してみよう」ぐらいの気軽な気持ちで読んでいただければと思います。

参考までに難易度を振っておきました。必要に応じて読めそうな部分だけを読んでいただいて大丈夫です。①と②以外は独立して読めるものとなっています。

それでは、順番に紹介していきましょう！

応用編の目次（今回の記事です！）

応用①：「関数」の間の非自明な関係式が得られる（難易度：★★）

応用②：「数列」の間の非自明な関係式が得られる（難易度：★★）

応用③：ヘッケ作用素と2次のゼータ（難易度：★★★）

応用④：素数を表現する2次形式（難易度：★★★★★）

応用⑤：楕円曲線とフェルマーの最終定理（難易度：★★★★）

おわりに

参考文献

導入編の目次（前回の記事）
導入①：三角関数のおさらい
導入②：モジュラー形式とは？
導入③：これだけは覚えて欲しい２つのモジュラー形式
導入④：q-展開とカスプ形式

応用①：「関数」の間の非自明な関係式が得られる（難易度：★★）

最初のトピックとして、保型形式であるような２つ（ないしは３つ）の関数の間に「想像もつかないような関係式」が成り立つ、というお話を紹介します。

たとえば、２つの正規化されたアイゼンシュタイン級数 $E_{4}(z)$ と $E_{8}(z)$ を考えましょう。これらの間にどんな関係が成り立つでしょうか。

定義を思い出すと

$\displaystyle E_{4}(z) = \frac{1}{2\zeta(4)} \sum_{(m, n) \in \mathbb{Z}^2\setminus \{(0, 0)\}} \frac{1}{(mz+n)^{4}}$

$\displaystyle E_{8}(z) =\frac{1}{2\zeta(8)} \sum_{(m, n) \in \mathbb{Z}^2\setminus \{(0, 0)\}} \frac{1}{(mz+n)^{8}}$

でした。

どちらもアイゼンシュタイン級数なので、似ていることは似ているのですが、何か関係式が見出せそうな気はあまりしません。

これに対しては、次のような驚きの関係式が成り立ちます：

$\displaystyle E_{4}(z)^2 = E_{8}(z) \tag{1}$

びっくりするぐらい綺麗にまとまりましたね。

級数の形に直すと

$\displaystyle \left(\frac{1}{2\zeta(4)} \sum_{(m, n) \in \mathbb{Z}^2\setminus \{(0, 0)\}} \frac{1}{(mz+n)^{4}}\right)^2 = \left(\frac{1}{2\zeta(8)} \sum_{(m, n) \in \mathbb{Z}^2\setminus \{(0, 0)\}} \frac{1}{(mz+n)^{8}}\right)$

ですが、これだけ見せられるとよりびっくりします。

もう一つ、同じく正規化されたアイゼンシュタイン級数 $E_{4}(z), E_{6}(z), E_{10}(z)$ を考えると

$\displaystyle E_{4}(z) E_{6}(z) = E_{10}(z) \tag{2}$

という関係式が成り立ちます。

これも級数の形にすると

$\displaystyle \begin{align*} \left(\frac{1}{2\zeta(4)} \sum_{(m, n) \in \mathbb{Z}^2\setminus \{(0, 0)\}} \frac{1}{(mz+n)^{4}}\right)\times \left(\frac{1}{2\zeta(6)} \sum_{(m, n) \in \mathbb{Z}^2\setminus \{(0, 0)\}} \frac{1}{(mz+n)^{6}}\right) \\ = \frac{1}{2\zeta(10)} \sum_{(m, n) \in \mathbb{Z}^2\setminus \{(0, 0)\}} \frac{1}{(mz+n)^{10}} \end{align*}$

ですが、これが成り立つというのはちょっと信じがたいですね。

このような関係式は他にもたくさん作ることができます。

式 $(1)$ と式 $(2)$ はどちらもアイゼンシュタイン級数の間の非自明な関係式ですが、重さだけに着目すると次のような法則が観察されます：

式 $(1)$ の左辺は、重さ $4$ と重さ $4$ をかけると重さ $8$ になっている（ $4 + 4 = 8$ ）
式 $(2)$ の左辺は、重さ $4$ と重さ $6$ をかけると重さ $10$ になっている（ $4 + 6 = 10$ ）

一般論として、重さ $k$ のモジュラー形式 $f(z)$ と重さ $l$ のモジュラー形式 $g(z)$ を掛け合わせた $f(z) g(z)$ は、重さ $k+l$ のモジュラー形式になります。

実際、 $f(z)g(z)$ に変換 $S$ （ $z$ を $-\frac{1}{z}$ に置き換える）を適用すると、 $f(z), g(z)$ の保型性より

$f(-\frac{1}{z})g(-\frac{1}{z}) = (-z)^k \, f(z)\; (-z)^{l} \, g(z) = (-z)^{k+l} \, f(z)g(z)$

が成り立つので、重さ $k+l$ になることがわかります。

そのため、重さに関して辻褄が合わないと等式が成り立たないわけですね。その意味で、式 $(8)$ と式 $(9)$ は重さの条件はクリアします。

一方で、重さが一緒のモジュラー形式が２つあったとして、それらの間にちょうど定数倍の関係があるものなのでしょうか。

実は、そこには驚くべき事情があったのです。鍵となるのはモジュラー形式のベクトル空間です。

一般論に入りますが、重さ $k$ のモジュラー形式 $f(z), g(z)$ があったとき、 $f(z) + g(z)$ も重さ $k$ のモジュラー形式になります。上で「掛け算」のときとまったく同じ議論で示せます。

また、重さ $k$ のモジュラー形式 $f(z)$ に対して、複素数 $c$ をかけた $c \, f(z)$ もまた重さ $k$ のモジュラー形式になります。

何がいいたいかというと、重さ $k$ のモジュラー形式全体の空間を考えたときに、これは複素係数のベクトル空間になっているというのです。この空間を $M_k$ とおきましょう。

また同様に、重さ $k$ のカスプ形式全体のなすベクトル空間を $S_k$ とおきましょう。重さが等しいカスプ形式同士も、和や複素数倍に対して閉じていることは簡単に示せます。明らかに、 $S_k \subset M_k$ は部分ベクトル空間になっていますね。

ここで面白いことは、これらのベクトル空間 $M_k, S_k$ が有限次元であり、次元がよくわかっているということです。次元を調べることで、重さ $k$ のモジュラー形式の間の関係式があぶり出されるのです。

まず、導入編②で述べたことを使って、次の基本的な事実をいうことができます：

重さ $0$ のモジュラー形式は定数のみ。したがって、次元は $1$ 。
重さが奇数のモジュラー形式は $0$ のみ。したがって、次元は $0$ 。

よって、重さ $k \geq 2$ が偶数の場合に次元を決定すれば十分です。

以下では、 $M_k$ の（複素係数のベクトル空間としての）次元を $\operatorname{dim}_{\mathbb{C}} M_k$ 、同様に $S_k$ の（複素係数のベクトル空間としての）次元を $\operatorname{dim}_{\mathbb{C}} S_k$ とします。

このとき、次の表のような事実が成り立ちます：

重さ $k$	$\operatorname{dim}_{\mathbb{C}} M_k$	$\operatorname{dim}_{\mathbb{C}} S_k$
$2$	$\mathbf{0}$	$0$
$4$	$1$	$0$
$6$	$1$	$0$
$8$	$1$	$0$
$10$	$1$	$0$
$12$	$2$	$\mathbf{1}$
$14$	$1$	$0$
$16$	$2$	$1$
$18$	$2$	$1$
$20$	$2$	$1$
$22$	$2$	$1$
$24$	$3$	$\mathbf{2}$

注目して欲しいのは、まず $k = 2$ のときの次元が $0$ であることです。重さ $2$ のモジュラー形式は、 $0$ 以外に存在しないというわけです。（アイゼンシュタイン級数も重さ $2$ のときは定義されませんでした。）

また、 $k$ が $4$ 以上のとき、 $M_k$ は $1$ 以上となります。これは各 $k$ に対して、少なくともアイゼンシュタイン級数 $E_k(z)$ がいるからですね。たしかに $E_k(z)$ はカスプ形式ではないモジュラー形式でした。

また、 $k = 4, 6, 8, 10$ まではモジュラー形式の次元は $1$ です。（カスプ形式の次元は $0$ です。）

状況が変わるのが $k = 12$ のときで、このときはモジュラー形式の次元が $2$ になっています。カスプ形式の次元が $1$ に上がっているので、その分独立な基底が増えたという感じですね。

察しのいい読者の方は思い出したのではないかと思います。そう、ラマヌジャンのデルタは重さ $12$ のカスプ形式でしたね！！

ラマヌジャンのデルタがいるので、新しくカスプ形式の空間ができたというわけです。それまでの重さではカスプ形式は存在しなかったというわけです。なるほど、それは確かにラマヌジャンのデルタは重要そうに思えます。

それ以降は、基本的には $k$ が $12$ の倍数になるたびに $S_k$ の次元が $+1$ されます。これに合わせて $M_k$ の次元も $+1$ されます。

$\begin{cases} \operatorname{dim}_{\mathbb{C}} M_{k+12} = \operatorname{dim}_{\mathbb{C}} M_{k} + 1 \\ \operatorname{dim}_{\mathbb{C}} S_{k+12} = \operatorname{dim}_{\mathbb{C}} S_{k} + 1 \end{cases}$ （ただし、 $k\neq 2$ ）

やはりこれも、ラマヌジャンのデルタが原因です。

重さが $k$ のモジュラー形式 $f(z) \in M_k$ があったときに

$f(z) \Delta(z)$

は重さ $k+12$ のカスプ形式になります。

この形以外の新しいカスプ形式は $S_{k+12}$ には存在しないので

$\operatorname{dim}_{\mathbb{C}} S_{k+12} = \operatorname{dim}_{\mathbb{C}} M_{k}$

が成立します。

また、 $E_k(z)$ はカスプ形式ではないモジュラー形式でしたから、この分によって

$\operatorname{dim}_{\mathbb{C}} M_{k} = \operatorname{dim}_{\mathbb{C}} S_{k} + 1$ 　（ $k \neq 2$ ）

となります。

以上を組み合わせると、 $k\neq 2$ に対し

が成り立つので、重さ $12$ ごとに次元が $+1$ されるわけです。

結局、モジュラー形式やカスプ形式の空間は、アイゼンシュタイン級数 $E_k(z)$ とラマヌジャンのデルタ $\Delta(z)$ からできていたというわけですね。彼らは単なるモジュラー形式の例であっただけでなく、ある意味でモジュラー形式のすべてであったというわけです。

もちろん、他にも重要なモジュラー形式の例は存在しますので、これがすべてというのは少し言い過ぎかもしれません。（テータ関数とかイータ関数とか。）

ただ、これらが重さに応じて $E_k(z)$ や $\Delta(z)$ の線形結合で表せるというのは、とても重要な事実ですね

さて、本題の関係式に戻りましょう。

$\displaystyle E_{4}(z)^2 = E_{8}(z) \tag{1再掲}$

左辺も右辺も重さ $8$ のモジュラー形式です。次元を考えると、 $\operatorname{dim}_{\mathbb{C}} M_8 = 1$ なのでした。ということは、重さ $8$ のすべてのすべてのモジュラー形式は、複素数の定数倍の関係にあるということですね。

つまり、複素数 $c$ が存在して

$\displaystyle E_{4}(z)^2 = c E_{8}(z)$

が成り立つことがわかってしまうというわけです。

あとは、 $z \to i\infty$ の正則性を使って両辺の極限をとると

$\displaystyle \lim_{z \to i\infty} E_{4}(z)^2 = c \lim_{z \to i\infty } E_{8}(z) \tag{3}$

が成り立つことがわかります。（定数 $c$ は極限とっても $c$ のままということです。）

一方、正規化されたアイゼンシュタイン級数 $E_4(z)$ と $E_8(z)$ の $q$ -展開を考えると

$\displaystyle E_4(z) = 1 + 240 \sum_{n = 1}^{\infty} \sigma_{3}(n)\, q^n$

$\displaystyle E_8(z) = 1 + 480 \sum_{n = 1}^{\infty} \sigma_{7}(n)\, q^n$

なのでした。

$z\to i\infty$ の極限において $q\to 0$ となります。これにより $\lim_{z\to i\infty} E_4(z), \; \lim_{z\to i\infty} E_8(z)$ は $q$ -展開の定数項に一致するわけですね。つまり

$\displaystyle \lim_{z\to i\infty} E_4(z) = 1$

$\displaystyle \lim_{z\to i\infty} E_8(z) = 1$

が成り立ちます。あとは式 $(3)$ に代入すれば定数が $c = 1$ であることがわかるという寸法です。

まとめると、次のような方法で非自明な等式を見つけることができてしまうわけですね：

重さ $k$ のモジュラー形式の空間の次元が $1$ であるとする
次元 $1$ より、重さ $k$ の二つのモジュラー形式 $f(z), g(z)$ の間に定数倍の関係がある $f(z) = c\,g(z)$
$z \to i\infty$ の正則性より、 $q$ -展開の定数項を比較することで、定数 $c$ が決定できる

いやー、これは面白いですね！！

次元が $2$ 以上の場合は同じようにはいきませんが、少なくとも線型結合でかけることが分かるので嬉しいことは多いです。カスプ形式の空間だけを考えることで次元 $1$ に出来ることもあるので、色々と応用の幅は広がります。

応用②：「数列」の間の非自明な関係式が得られる（難易度：★★）

応用①では、関数の間の関係式を紹介しました。関数の関係式なので、整数論にはあまり関係なさそうな気がしてします。

一方で、保型形式は整数論で重要な役割を果たすとよく言われます。これはいったいどういうことなのでしょうか。

重さ $k$ の２つのモジュラー形式 $f(z), g(z)$ の間に、応用①でやったような方法を用いて関係式

$f(z) = c\, g(z)$

が得られたとしましょう。

ここで、左辺と右辺をそれぞれ $q$ -展開したいと思います。するとそれぞれ

$\displaystyle f(z) = \sum_{n = 0}^{\infty} a_n(f) \, q^n$

$\displaystyle c\,g(z) = \sum_{n = 0}^{\infty} c\, a_n(g) \, q^n$

のように書けるわけです。両者はべき級数の間の等式だと思うと、任意の $n$ について

$a_n(f) = c\, a_n(g)$

が成り立つということが分かってしまいます。つまり、数列の間の等式が得られたというわけです。

ここで正規化されたアイゼンシュタイン級数 $E_{2k}$ を思い出しましょう。 $E_{2k}(z)$ の $q$ -展開には

$\displaystyle E_{2k} = 1 - \frac{4k}{B_{2k}} \sum_{n=1}^{\infty} \sigma_{2k-1}(n)\, q^n$

のように、係数に「約数関数 $\sigma_{2k-1}(n)$ 」という数論的に重要な数列が入っていました。

$E_{4}(z)^2 = E_8(z)$ という関係式から、両辺を $q$ -展開することによって

$\displaystyle \left(1 + 240 \sum_{n = 1}^{\infty} \sigma_{3}(n)\, q^n \right)^2 = 1 + 480 \sum_{n = 1}^{\infty} \sigma_{7}(n)\, q^n$

という関係式を得ることができます。左辺を展開すると

$\displaystyle 1 + 480 \sum_{n = 1}^{\infty} \sigma_{3}(n)\, q^n + 240^2\left( \sum_{n = 1}^{\infty} \sigma_{3}(n)\, q^n \right) \left( \sum_{n = 1}^{\infty} \sigma_{3}(n)\, q^n \right)$

となりますが、両辺の $q^n$ の係数を比較することで次の等式を得ることができます：

$\displaystyle \sigma_7(n) = \sigma_3(n) + 120\sum_{m=1}^{n-1}\sigma_3(m) \sigma_3(n-m) \tag{4}$

これはまさに約数関数の間の非自明な等式となっていて、面白いですね！！

こんな風に数論的に面白い関係式がバンバン出てきたら楽しそうですね！

もう一つ紹介したいのはラマヌジャンの合同式です。

$\tau(n) \equiv \sigma_{11}(n) \pmod{691} \tag{5}$

これも相当に非自明な合同式だと思います。ラマヌジャンのタウ関数と約数関数の間にどうしてこんな関係が成り立つというのでしょう。そして $691$ はどこから出てきたのか。

種明かしをすると、重さ $12$ のモジュラー形式の間の関係式

$\displaystyle E_{12}(z) - E_6^2(z) = \frac{65520 + 1008\cdot 691}{691} \Delta(z) \tag{6}$

から作ることができます。

重さ $12$ のモジュラー形式の次元は $2$ なので、応用①の方法ではうまくいかないと思うかもしれません。ところが、カスプ形式の方は次元 $1$ なので、これを使うことができます。

$E_{12}(z) - E_6^2(z)$ はそれぞれの定数項 $1$ を打ち消しているので、カスプ形式になります。ラマヌジャンのデルタはもちろんカスプ形式なので、両辺が重さ $12$ のカスプ形式になるわけですね。よって $E_{12}(z) - E_6^2(z)$ と $\Delta(z)$ の間に定数倍の関係が示されるわけです（式 $(6)$ ）。

合同式の作り方ですが、式 $(6)$ の両辺を $691$ 倍した上で $q^n$ の係数を比較します。これは複雑な関係式になりますが、 $\bmod{691}$ をとると

$65520\, \sigma_{11}(n) \equiv 65520\, \tau(n) \pmod{691}$

が成立します。一見、左辺は消えてしまいそうに思うのですが、 $E_{12}(z)$ の係数の分母には $691$ が出てくるので、うまいこと $691$ 倍が打ち消されてくれるのですね。 $65520$ と $691$ は互いに素なので、ラマヌジャンの合同式 $(5)$ が導かれるというわけです。面白いですね。

計算過程を詳しく知りたい方はこちらの記事をどうぞ。
tsujimotter.hatenablog.com

応用③：ヘッケ作用素と2次のゼータ（難易度：★★★）

今度はラマヌジャンのデルタ $\Delta(z)$ に関する話です。

ラマヌジャンのデルタの $q$ -展開は、 $\tau(n)$ を用いて

$\displaystyle \Delta(z) = \sum_{n=1}^{\infty} \tau(n)\,q^n \tag{7}$

と表せるのでした。

以前書いた記事では、ラマヌジャンのデルタから「ゼータ関数（L関数）」を作ることができるという話をしています：
tsujimotter.hatenablog.com

この記事の内容を簡単に振り返ります。 $\tau(n)$ を形式的に並べて作る

$\displaystyle L(s, \Delta) = \sum_{n=1}^\infty \frac{\tau(n)}{n^s} \tag{8}$

という関数をラマヌジャンのゼータといいます。これは 2次のオイラー積

$\displaystyle L(s, \Delta) =\prod_{p}\frac{1}{1 - \tau(p) p^{-s} + p^{11} p^{-2s}} \tag{9}$

という形で表すことができました。右辺は素数 $p$ に関する無限積の形で表されています。

変形の鍵となったのは、ラマヌジャンのタウ関数に成り立つ次の等式です：

$\tau(p^k) = \tau(p) \tau(p^{k-1}) - p^{11} \tau(p^{k-2}) \tag{10}$

この等式から2次のオイラー積が導かれることは、上の記事で説明していました。問題はこの等式がいかに導かれるかという点です。

ラマヌジャンのタウ関数同士の関係なので、応用②でやったような2つの保型形式を使う方法は、今回は適用できなさそうです。ここで使えるのがヘッケ作用素です。

重さ $k$ のモジュラー形式やカスプ形式の空間 $M_k, S_k$ はベクトル空間であったことを思い出しましょう。自然数 $n$ に対して

$T_k(n)\colon M_k \longrightarrow M_k$

という線形写像を構成することができます。つまり、重さ $k$ のモジュラー形式 $f$ を、重さ $k$ の別のモジュラー形式 $T_k(n)\,f$ に写すような線形写像ですね。 $T_k(n)$ をヘッケ作用素といいます。

この写像はカスプ形式をカスプ形式に写すので、 $S_k$ に制限させると

$T_k(n)\colon S_k \longrightarrow S_k$

となります。

一般に、 $f \in M_k$ （あるいは $f \in S_k$ ）が与えられたときに、 $f$ に $T_k(n)$ を適用した $T_k(n) \,f$ はさまざまなモジュラー形式（カスプ形式）になりえます。これがもし

$T_k(n)\, f = \lambda_n \,f$ 　（ $\lambda_n \in \mathbb{C}$ ）

を満たす（つまり、元のモジュラー形式（カスプ形式）の定数倍になる）のであれば、 $\lambda_n$ を $T_k(n)$ の固有値、 $f$ を $T_k(n)$ の固有形式といいます。

任意の自然数 $n$ について、ある $f$ がすべての $T_k(n)$ に対する固有形式になっているとき、 $f$ は $T_k(n)$ の同時固有形式であるといいます。つまり

$T_k(1)\, f = \lambda_1 \,f$

$T_k(2)\, f = \lambda_2\, f$

$T_k(3)\, f = \lambda_3\, f$

$T_k(4)\, f = \lambda_4\, f$

$\vdots$

等々となるような、 $\lambda_1, \lambda_2, \lambda_3, \lambda_4, \ldots \in \mathbb{C}$ が存在するということですね。

ラマヌジャンのデルタ $\Delta(z)$ は重さ $12$ のカスプ形式なので、 $\Delta(z) \in S_{12}$ となります。 $S_{12}$ の次元は $1$ なので $T_{12}(n)\, \Delta(z)$ は $\Delta(z)$ の定数倍となります。よって、 $\Delta(z)$ は自動的に $T_{12}(n)$ の同時固有形式となります。

さらに面白いのは、その固有値が $\tau(n)$ になることです。すなわち

$T_{12}(n)\, \Delta = \tau(n) \Delta \tag{11}$

となるわけですね。

式 $(11)$ の両辺の $q$ -展開を比較することで（左辺はヘッケ作用素の定義式を展開することで）、式 $(10)$ の関係式を得ることができます。面白いですね！！

同様に、 $f\in M_k$ をモジュラー形式とします。このとき、 $f$ に付随するL関数を

$\displaystyle L(s, f) := \sum_{n=1}^{\infty} \frac{a_n(f)}{n^s} \tag{12}$

によって定義することができます。

特に、 $f$ が $a_1(f) = 1$ と正規化されているような、ヘッケ作用素 $T_k(n)$ に対する同時固有形式とします。すると $f$ の $T_k(n)$ に対する固有値は $a_n(f)$ となります。このことから、ラマヌジャンのゼータと同じ要領で、オイラー積表示

$\displaystyle L(s, f) = \prod_{p} \frac{1}{1 - a_p(f)p^{-s} + p^{k-1} p^{-2s}} \tag{13}$

が得られます。

つまり、ラマヌジャンのゼータは、正規化された固有形式から2次のオイラー積を持つゼータ関数（2次のゼータ）が得られる、という話の具体的な一例だったというわけですね！

応用④：素数を表現する2次形式（難易度：★★★★★）

次の話題は、素数 $p$ が整数 $x, y$ を用いて

$p = x^2 + xy + 6y^2 \tag{14}$

と書ける条件についてです。この話は、概要を理解するだけであればそれほど難しくないのですが、ちゃんと理解しようとすると難易度が大きく上がります。

条件を明らかにするため、式 $(14)$ の右辺を分解してみると

$p = x^2 + xy + 6y^2 = (x + y\frac{1+\sqrt{-23}}{2}) (x + y\frac{1-\sqrt{-23}}{2})$

のように表せます。このことから、この問題が虚2次体 $\mathbb{Q}(\sqrt{-23})$ の整数環 $\mathbb{Z}[\frac{1+\sqrt{-23}}{2}]$ において $p$ がいつ分解するか、と関係することがわかります。

一方で、整数環 $\mathbb{Z}[\frac{1+\sqrt{-23}}{2}]$ は単項イデアル整域（PID）ではないので、話はそう簡単ではありません。単に $p$ が素イデアルの積に分解するかどうかだけでは十分ではないのです。

そこで、 $\mathbb{Q}(\sqrt{-23})$ のさらに上の ヒルベルト類体 $H$ というものを考えます。 $H/\mathbb{Q}$ で $p$ が完全分解することが $p = x^2 + xy + 6y^2$ と書けることの必要十分条件というわけです。

ところで「類体論」によると、素数 $p$ が $K/\mathbb{Q}$ で分解するかどうかが「 $p\bmod{N}$ 」によって表されるのは、 $K/\mathbb{Q}$ がアーベル拡大のときに限られるのでした。アーベル拡大ではない場合は、類体論によっては法則を見いだすことが原理的にできないのです。

残念ながら、今回の $H/\mathbb{Q}$ はアーベル拡大ではないガロア拡大であり、どうしたものかというわけです。

こんなときに使えるのがモジュラー形式です。次のような、モジュラー形式を考えます：

$\displaystyle f(z) = q \prod_{n=1}^{\infty} (1-q^n)(1-q^{23n}) \tag{15}$

この $f(z)$ はこれまで扱ってきたようなフルモジュラーなモジュラー形式ではないことに注意します。「レベル」という構造が加わり、重さ $1$ でレベル $23$ のモジュラー形式となります。

「重さ $1$ 」であることに驚いた方もいるかもしれません。レベルという構造が加わったことで、よりモジュラー形式のバリエーションが増え、重さ $1$ のものも現れるようになったというわけですね。ただ、細かいことは今回の記事では置いておきましょう。

$f(z)$ の $q$ -展開を計算して、 $p$ 次の係数を $a_p(f)$ とします。すると、なんと次が成り立つのだそうです：

$p = x^2 + xy + 6y^2 \;\; \Longleftrightarrow \;\; p$ が $H/\mathbb{Q}$ で完全分解 $\;\; \Longleftrightarrow \;\; a_p(f) = 2$
（ただし、有限個の $p$ を除く。）

これは驚きの結果だと思うのですが、「 $H/\mathbb{Q}$ で完全分解すること」と「 $a_p(f) = 2$ であること」がなんと同値だというのです。

これには非常に深い理由があるのですが、簡単に説明できるようなものではなさそうです。上で挙げた法則の裏には、図に示すような深く深い背景があります。

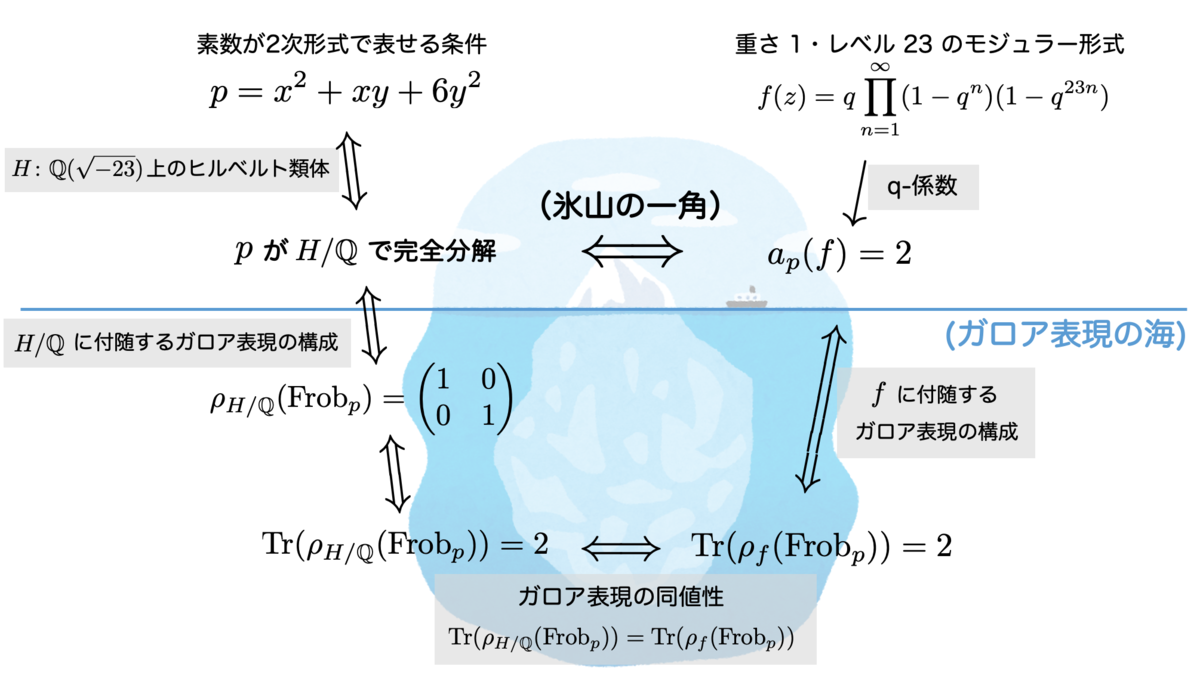
深海の底のような深い場所に大きな法則があり、素数の分解法則とモジュラー形式が繋がっているのです。上の法則は、さながら深海の上に現れた「氷山の一角」といったところでしょうか。

以下ではなんとかかいつまんで説明しようと試みます。かなり端折って説明しますが、より詳しく知りたい方は以下の記事か、元の伊藤先生の記事をご確認ください：
tsujimotter.hatenablog.com

「素数 $p$ が $H/\mathbb{Q}$ で完全分解するか」という問題は、一旦 $\mathbb{Q}$ の代数閉包 $\overline{\mathbb{Q}}$ まで持ち上げて考えることになります。

$\overline{\mathbb{Q}}/\mathbb{Q}$ のガロア群を絶対ガロア群 $G_\mathbb{Q}$ といいますが、 $G_\mathbb{Q}$ の中には素数 $p$ の分解法則を司るフロベニウス $\operatorname{Frob}_p$ という元が存在します。

「フロベニウスって何だろう」という方には、こちらの記事がおすすめです：
tsujimotter.hatenablog.com

実際、 $\operatorname{Frob}_p \colon \overline{\mathbb{Q}} \to \overline{\mathbb{Q}}$ を $H$ に制限させたときに、次が同値な条件となります。

$\operatorname{Frob}_p|_H$ が $\operatorname{Gal}(H/\mathbb{Q})$ の単位元 $\;\; \Longleftrightarrow \;\;$ $p$ が $H/\mathbb{Q}$ で完全分解する
（ただし、有限個の素数 $p$ を除く）

話をモジュラー形式に結びつけるために、ガロア表現の問題にします。 $\operatorname{Gal}(H/\mathbb{Q}) \simeq S_3$ なので、 $S_3$ の既約表現を使って、 $\operatorname{Gal}(H/\mathbb{Q})$ を $\operatorname{GL}_2(\mathbb{C})$ に埋め込みます。これにより、単位元が単位行列に送られます：

$\begin{eqnarray} \tau \;\colon \;\;& \operatorname{Gal}(H/\mathbb{Q}) & \simeq S_3 \hookrightarrow & \operatorname{GL}_2(\mathbb{C}), \\ & \operatorname{id} & \longmapsto & \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \end{eqnarray}$

また、 $G_{\mathbb{Q}}$ の元を $H$ に制限することによって得られる全射 $G_\mathbb{Q} \twoheadrightarrow \operatorname{Gal}(H/\mathbb{Q})$ を考えます。これらを合成することによって得られる写像

$\rho_{H/\mathbb{Q}} \colon G_\mathbb{Q} \twoheadrightarrow \operatorname{Gal}(H/\mathbb{Q}) \simeq S_3 \hookrightarrow \operatorname{GL}_2(\mathbb{C})$

は2次元のガロア表現となります。

$\rho_{H/\mathbb{Q}}$ によって、 $\operatorname{Frob}_p \in G_{\mathbb{Q}}$ を送ったときに単位行列

$\rho_{H/\mathbb{Q}}(\operatorname{Frob}_p) = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$

となれば、 $p$ は $H/\mathbb{Q}$ で完全分解します。（逆も言えます。）

一方、式 $(15)$ で定義したモジュラー形式 $f(z)$ には、 $f(z)$ に付随する2次元のガロア表現 $\rho_f$ が存在します。「付随する」というのは、 $f$ の $q$ -係数を $a_p(f)$ としたとき、有限個を除く素数 $p$ に対して

$\operatorname{Tr}( \rho_f(\operatorname{Frob}_p) ) = a_p(f) \tag{16}$

が成り立つということです。

これ自体は大定理ですが、受け入れて進みましょう。つまり、モジュラー形式 $f$ からガロア表現 $\rho_f$ が得られたというわけですね。

ここで重要なことは、先ほどのガロア表現 $\rho_{H/\mathbb{Q}}$ と今作った $\rho_{f}$ が同値だということです。ガロア表現が同値というのは、（有限個を除く）素数 $p$ についてのフロベニウス $\operatorname{Frob}_p$ をガロア表現 $\rho_{H/\mathbb{Q}}$ と $\rho_{f}$ で送ったときに、それぞれの行き先のトレースが等しいこと、と言い換えられます。

要するに、有限個の素数 $p$ を除いて

$\operatorname{Tr}( \rho_{H/\mathbb{Q}}(\operatorname{Frob}_p) ) = \operatorname{Tr}( \rho_{f}(\operatorname{Frob}_p) )$

が成り立つわけです。ここが核心といえます。（図の深海の底ですね。）

あとは $a_p(f) = \operatorname{Tr}( \rho_{f}(\operatorname{Frob}_p) )$ であることと、「完全分解 ⇔ 単位行列」なのでトレースが $2$ であることから、以下の同値をいうことができます。

$H/\mathbb{Q}$ において $p$ が完全分解
$\Longleftrightarrow \;\;$ $a_p(f) = \operatorname{Tr}( \rho_{f}(\operatorname{Frob}_p) ) = \operatorname{Tr}( \rho_{H/\mathbb{Q}}(\operatorname{Frob}_p) ) = 2$

以上により、 $p$ が $H/\mathbb{Q}$ で完全分解されるかどうかが、モジュラー形式 $f$ の $q$ -係数の値を見ることによってわかるという、大変摩訶不思議な現象が説明できるわけですね。いやー、面白い！！

核心にあったのは、２つのガロア表現 $\rho_{H/\mathbb{Q}}$ と $\rho_f$ の同値性という問題でした。「 $p = x^2 + xy + 6y^2$ と書ける素数の法則」には、こんなに深い背景があったのですね。改めて図を再掲します。

応用⑤：楕円曲線とフェルマーの最終定理（難易度：★★★★）

最後の話題として、フェルマーの最終定理の話をしたいと思います。

よく知られているように、フェルマーの最終定理は1995年にアンドリュー・ワイルズによって証明されました。このとき使われた方針は、 $\mathbb{Q}$ 上の楕円曲線とモジュラー形式の間の深い関係「志村-谷山予想」を証明することでした。ここでは志村-谷山予想を紹介します。

まず、 $\mathbb{Q}$ 上の楕円曲線とは

$E\colon y^2 = x^3 +ax^2 + bx + c \tag{17}$

の形で表せる曲線であって、右辺の $x$ についての $3$ 次式が重根を持たないものをいいます。 $a, b, c$ は有理数です。だから「 $\mathbb{Q}$ 上の」楕円曲線ということですね。

志村-谷山予想とは、任意の $\mathbb{Q}$ 上の楕円曲線は「モジュラーである」という主張です。ただ、「モジュラーである」ということの意味が分からなければ何の意味もないので、より詳しく述べていきましょう。

楕円曲線 $E$ には、素数 $p$ 対して「 $\bmod{p}$ の（無限遠点を含む）解の個数 $\# E_p(\mathbb{F}_p)$ 」を数えることで

$a_p(E) = p+1 - \# E_p(\mathbb{F}_p) \tag{18}$

という量が定まります。この計算は冒頭に挙げた数学ガールでもやっています。

数学ガールを読んでいる方向けの補足：
数学ガールの方では、 $a_p(E) = p - s(p)$ と定義されています。 $s(p)$ は有限体上の解の個数なので、私の式とは数が $1$ だけずれているように思うかもしれません。しかし、上の式 $(18)$ で問題ないことがわかります。

実際、数学ガールの方は、 $s(p)$ を数える際に「無限遠点」を数えていないのです。私の方では、 $\# E_p(\mathbb{F}_p)$ を数える際に「無限遠点」を数えることにしています。だから、 $\# E_p(\mathbb{F}_p) = s(p) + 1$ となり、1個ずれてみえるわけですね。だから、 $a_p(E) = p+1 - \# E_p(\mathbb{F}_p)$ としても、 $a_p(E) = p - s(p)$ としてもどちらでもよいわけです。

一方、モジュラー形式 $f$ に対しては、これまでやってきたように $q$ -係数 $a_p(f)$ が定まるのでした。

与えられた $\mathbb{Q}$ 上の楕円曲線 $E$ に対して、あるモジュラー形式 $f$ が存在して、任意の $p$ に対して

$a_p(E) = a_p(f) \tag{19}$

が成り立つとき、 $\mathbb{Q}$ 上の楕円曲線 $E$ はモジュラーであるといいます。

これで志村-谷山予想の主張が理解できたでしょう。

定理（志村-谷山予想）

任意の $\mathbb{Q}$ 上の楕円曲線 $E$ はモジュラーである。

$E$ がモジュラーであるとは、あるモジュラー形式 $f$ が存在して、任意の素数 $p$ に対して

$a_p(E) = a_p(f) \tag{19再掲}$

が成り立つことをいう。

より詳細には、 $\mathbb{Q}$ 上の楕円曲線 $E$ に対しては（あとで出てくる）導手 $N$ と呼ばれる正の整数が定まります。モジュラー形式にも「レベル」という構造があるのですが、導手 $N$ の楕円曲線に対しては、重さ $2$ 、レベル $N$ のモジュラー形式 $f$ が対応します。

志村-谷山予想を証明する方針は、応用④でやったようにガロア表現を使うことです。

詳細は思い切り端折りますが、導手 $N$ の $\mathbb{Q}$ 上の楕円曲線 $E$ に対して2次元のガロア表現 $\rho_E$ が定まります。このとき、ある重さ $2$ 、レベル $N$ のモジュラー形式 $f$ が存在して、 $\rho_E$ と $\rho_f$ が存在することを示せばよいわけですね。

ただし、応用④では複素係数のガロア表現を考えていましたが、今度は素数 $\ell$ を用いた $\ell$ 進表現 $\rho_{E, \ell}, \; \rho_{f, \ell}$ を考えることになります。

ガロア表現が同値であれば、そのトレースが一致するわけなので

$a_p(E) = \operatorname{Tr}( \rho_{E, \ell}(\operatorname{Frob}_p) ) = \operatorname{Tr}( \rho_{f, \ell}(\operatorname{Frob}_p) ) = a_p(f)$

が成り立つというわけですね。

この記事の中で、志村-谷山予想の証明について、これ以上の踏み込んだ解説は不可能です。なにせ私が理解していないからです。

一方で、志村-谷山予想を仮定すると、どのようにしてフェルマーの最終定理が導かれるのかと言う点については、ある程度説明することができそうです。最後の仕上げにこれだけやってしまいましょう。

以下の図のような流れで進めていきます：

（志村-谷山予想 $\Longrightarrow$ フェルマーの最終定理の証明）
背理法により証明します。素数 $l \geq 5$ についての方程式 $x^l + y^l = z^l$ に、 $abc\neq 0$ なる整数解 $(x, y, z) = (a, b, c)$ があると仮定しましょう：

$a^l + b^l = c^l$

このとき、解 $(a, b, c)$ を用いて、次のような楕円曲線を得ることができます：

$E_l\colon y^2 = x(x+a^l)(x-b^l) \tag{20}$

右辺を展開すると $x$ についての $3$ 次式になっていて、かつ、重根を持たないので楕円曲線です（係数も有理数なので $\mathbb{Q}$ 上でもある）。ゲルハルト・フライという人が発見したので、 $E_l$ はフライ曲線と呼ばれます。

フェルマーの最終定理に解があるとすると、フライ曲線と呼ばれる $\mathbb{Q}$ 上の楕円曲線が存在してしまうのですね。実は、このフライ曲線はとても「奇妙な」性質を持っているのだとか。

実際、右辺の根は $x = -a^l, 0, b^l$ なのですが

$-a^l$ と $0$ の差 $a^l$ が $l$ 乗数
$0$ と $b^l$ の差 $b^l$ が $l$ 乗数
$-a^l$ と $b^l$ の差が $b^l - (-a^l) = c^l$ で $l$ 乗数

となっていて、この点が「奇妙に」感じられるそうです。あとはこの「奇妙さ」をなんとかして「矛盾」に持ち込むことができれば「勝ち」というわけです。

この「奇妙さ」を象徴する量として、楕円曲線の判別式 $D$ および導手 $N$ があります。判別式とは、3次式の根の差の2乗を掛け合わせた量

$D = (- a^l - 0)^2(0 - b^l)^2(b^l - (-a^l))^2 = (abc)^{2l}$

です。導手 $N$ は $D$ を割り切るすべての素数 $p$ に $e(p)$ 乗したものを掛け合わせた量となっています。今回の場合は $e(p) = 1$ となり

$N = \prod_{p \mid D} p$

となるそうです。

追記2021.03.18：判別式の定義で二乗するのを忘れていたので、修正しました。それに伴って、下のリベの定理を若干修正しています。

志村-谷山予想を仮定すると、任意の $\mathbb{Q}$ 上の楕円曲線はモジュラーであるというのです。したがって、対応する重さ $2$ 、レベル $N$ のモジュラー形式 $f(z)$ が存在することになります。

ここで、リベ（Ribet）の定理を適用します。リベの定理を今回の限定的な状況に適用すると、次のことが言えます。

楕円曲線 $E$ を $E\colon y^2 = (x-A)(x-B)(x-C)$ として、その導手を $N$ とする。また、志村-谷山予想によって $E$ に対応する重さ $2$ ・レベル $N$ のモジュラー形式を $f(z)$ とする。

$N = LM$ （ $L$ と $M$ は正の整数）であって

条件１： $(A - B)(B - C)(C - A) = (\text{整数})^l \times (L \;\text{と互いに素な整数})$
条件２： $L$ は奇数で、 $L$ と $M$ は互いに素

という条件を満たすものが存在するとき、重さ $2$ 、レベル $M$ のカスプ形式 $g(z)$ であって、 $n \geq 1$ に対して $a_n(g)$ は整数であり

$a_n(f) \equiv a_n(g) \pmod{l}$

であるものが存在する。

つまり、重さ $2$ ・レベル $N$ のモジュラー形式 $f(z)$ から、重さ $2$ ・レベル $M = \frac{N}{L}$ のカスプ形式 $g(z)$ が作れるということです。 $M$ を小さくとることができれば、レベルが小さいカスプ形式が得られるわけです！

フライ曲線の解の差積を思い出すと、 $(abc)^l \times 1$ なので条件１を満たしています。このことからも、リベの定理がまさにフライ曲線のためのセッティングという感じがします。

また、 $N$ の約数として $2$ が取れます。（これはフェルマーの最終定理の解 $a, b, c$ のいずれかには、必ず偶数が入ってくるからです。）

よって、 $L = \frac{N}{2}, \; M = 2$ としてみましょう。すると、 $L$ は奇数であり、 $L$ と $M$ は互いに素なので、条件２も成立します。

リベの定理より、重さ $2$ ・レベル $2$ のカスプ形式 $g(z)$ であって、 $g(z) \neq 0$ であるものの存在が示されました。（楕円曲線の $a_n(E_l)$ がすべて $l$ で割り切れないことがわかり、このことから $a_n(f)$ が恒等的に $0$ にならないことが言えるので、 $g(z) \neq 0$ も言える。）