正十二面体群とPSL(2,5)：国際数学者会議PR企画の宣伝動画について

４年に一度、国際数学者会議（ICM: International Congress of Mathematicians）と呼ばれる大きな催しが行われます。フィールズ賞という、数学界の最高峰の賞が発表される会としても知られていますね。

次回、2022年にはロシアのサンクトペテルブルグにてICM 2022が開催されるようです。私がこの情報を知ったのは、ICM 2022の公式が出しているプロモーション企画の情報を、Springerさんのツイート経由で見たのがきっかけでした。

プロモーション企画のタイトルは "Surprising math user video contest" です。いかにも楽しそうなタイトルですね！

企画のページはこちらです：
icm2022.org

要するに、数学に関する面白い動画を投稿するコンテストのようですね。我こそはという方は挑戦してみてはいかがでしょうか。

特に見ていただきたいのは、ICM 2022公式が出している宣伝動画です。
www.youtube.com

動画を見てまず感じるのは、映像に登場する図がとてもきれいだということですね。それだけでもそそられますが、内容も大変面白く、私の心に深く刺さりました。

とはいえ、企画のプロモーション動画ということもあり、時間は短めで、かつ音声による説明はまったくありません。内容自体も結構高度なので、背景知識がないとなかなか理解するのは難しいかと思います。

そこで今回は、あくまで私の理解できた範囲で、このICMの動画の内容の解説を試みたいと思います。もちろん、私も１００％理解できているわけではないので、あやふやな点も多々あるかと思います。その点をご了承の上、見ていただけると嬉しいです。

テーマは

正十二面体群と $\operatorname{PSL}(2, \mathbb{F}_5)$ の不思議な同型について

です。大変面白いトピックなので、ぜひ最後まで読んでいただきたいです！

登場人物の紹介：正十二面体群と $\operatorname{PSL}(2, \mathbb{F}_5)$

まずは登場人物の紹介から始めましょう。

主役の一人は正十二面体です。正十二面体は、皆さんご存知の通り、12個の面を持つ多面体の一つであり、特に「すべての面が同一の正五角形で構成され、かつすべての頂点において接する面の数が等しい凸多面体」となっています。また、12個の面・20個の頂点・30個の辺を持ちます。

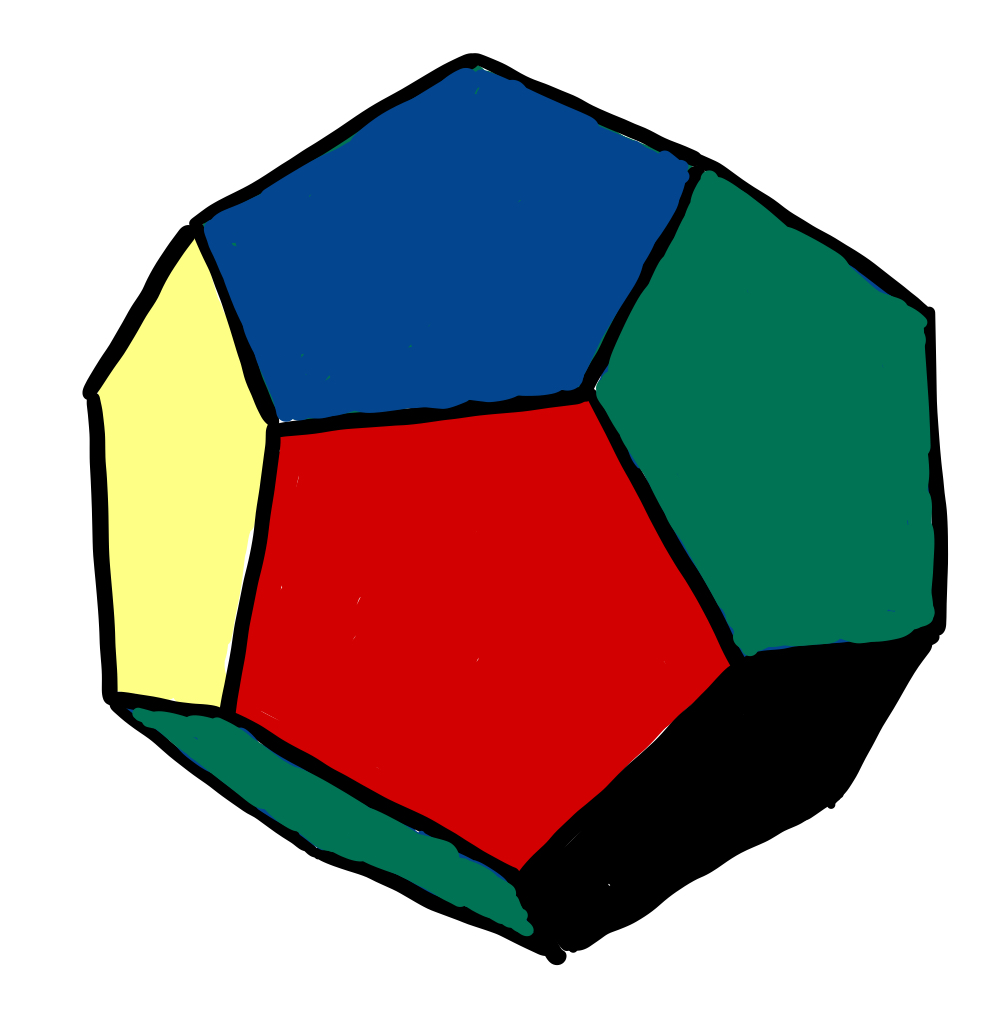
f:id:tsujimotter:20210425124629j:plain:w220

正十二面体は数多くの対称性を持った図形です。実際、数を数えてみましょう。まず、１つの向かい合う面の組に対して $1/5$ 回転させる対称性があります。他にも、１つの向かい合う頂点の組に対して $1/3$ 回転させる対称性や、１つの向かい合う辺の組に対して $1/2$ 回転させる対称性があります。最後に「何もしない対称性」を加えると

$\displaystyle \begin{align} &(5-1)\times \frac{12}{2} + (3-1)\times \frac{20}{2} + (2-1)\times \frac{30}{2} + 1 \\ &= 24 + 20 + 15 + 1 \\ &= 60 \end{align}$

となります。この60個の対称性のなす群が正十二面体群です。

また、正十二面体群は交代群 $A_5$ と同型であることも知られています。 $A_5$ は特に「位数最小の非可換単純群」として知られ、五次方程式が解けないメカニズムを説明するのに用いられますね。

交代群 $A_n$ は、 $n$ 点 $\{1, 2, 3, \ldots, n\}$ に対する任意の置換のなす群（対称群 $S_n$ ）の部分群であり、偶数個の互換の積で表される元全体のなす群です。

もう一人の主役は特殊線型群です。

一般に、 $R$ を環とします（ $R$ には $\mathbb{Z}$ や有限体 $\mathbb{F}_p$ などが入ります）。 $2\times 2$ の $R$ 係数正方行列であって、行列式が $1$ であるもの全体を考えると、これは乗法について群をなします。これを特殊線形群といい、 $\operatorname{SL}(2, R)$ と表します：

$\operatorname{SL}(2, R) := \left\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \; \middle| \; a, b, c, d \in R, \; ad - bc = 1 \right\}$

$\operatorname{SL}(2, R)$ の中には、単位行列と単位行列にマイナスをつけた行列

$I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \;\; -I = \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}$

が入っていて、これらで割ったものを特に $\operatorname{PSL}(2, R)$ と表します：

$\operatorname{PSL}(2, R) := \operatorname{SL}(2, R)\big/ \{\pm I\}$

要するに、マイナスがついた行列を同じものだと思うというわけですね。

$R = \mathbb{Z}, \; \mathbb{F}_p$ （有限体）としたときに、 $\operatorname{SL}(2, \mathbb{Z}), \; \operatorname{SL}(2, \mathbb{F}_p)$ が定義できるわけですが、これらの行列群が今回の主役の一角をなします。

なお、 $\operatorname{PSL}(2, \mathbb{F}_p)$ のことを、 $\operatorname{PSL}(2, \mathbb{Z}/p\mathbb{Z})$ と書いたり、単に $\operatorname{PSL}(2, p)$ と書くこともあります。

特に $p = 5$ としたとき、 $\operatorname{PSL}(2, \mathbb{F}_5)$ と正十二面体群 $A_5$ の間には、次のような非自明な群の同型

$\operatorname{PSL}(2, \mathbb{F}_5) \simeq A_5$

があります。これだけ見ると、なんでこの二つに群の同型があるのだろうかと不思議に思います。その背景を理解したいというのが、今回のメインテーマです。

ICMの動画で紹介されているように、実は次次節で紹介するモジュラー曲線 $X(5)$ というものを考えると、 $X(5)$ への群作用を通して上の同型が自然に見えてくるというのです。

目標は上の通りなのですが、とはいえいきなりモジュラー曲線 $X(5)$ を定義するのは、少し話が飛躍しすぎています。まずは基本的なモジュラー曲線 $X(1)$ や、必要な前提を説明していきましょう。

基本領域とポアンカレ円板、モジュラー曲線 $X(1)$

それでは、まずは行列のなす群 $\operatorname{SL}(2, \mathbb{Z})$ が、上半平面という空間に作用するという話から始めましょう。

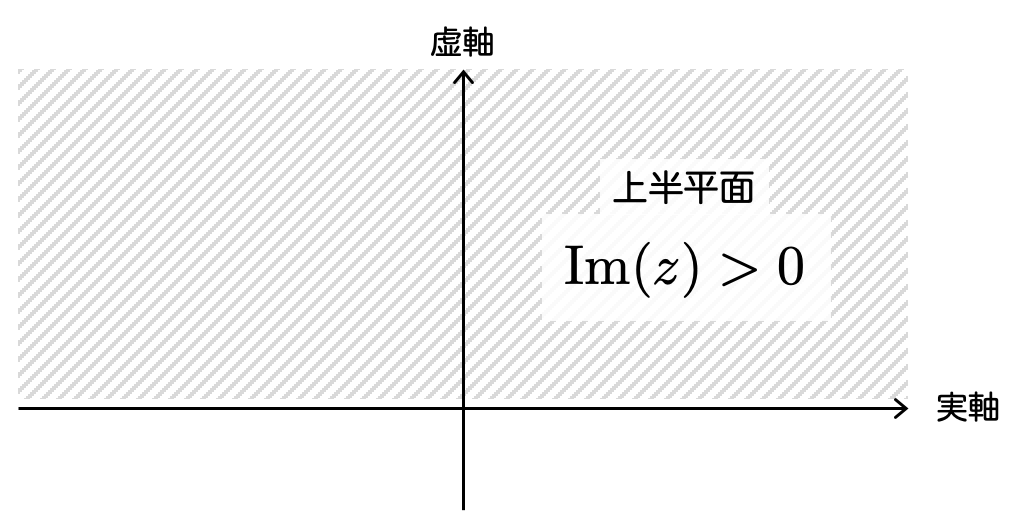
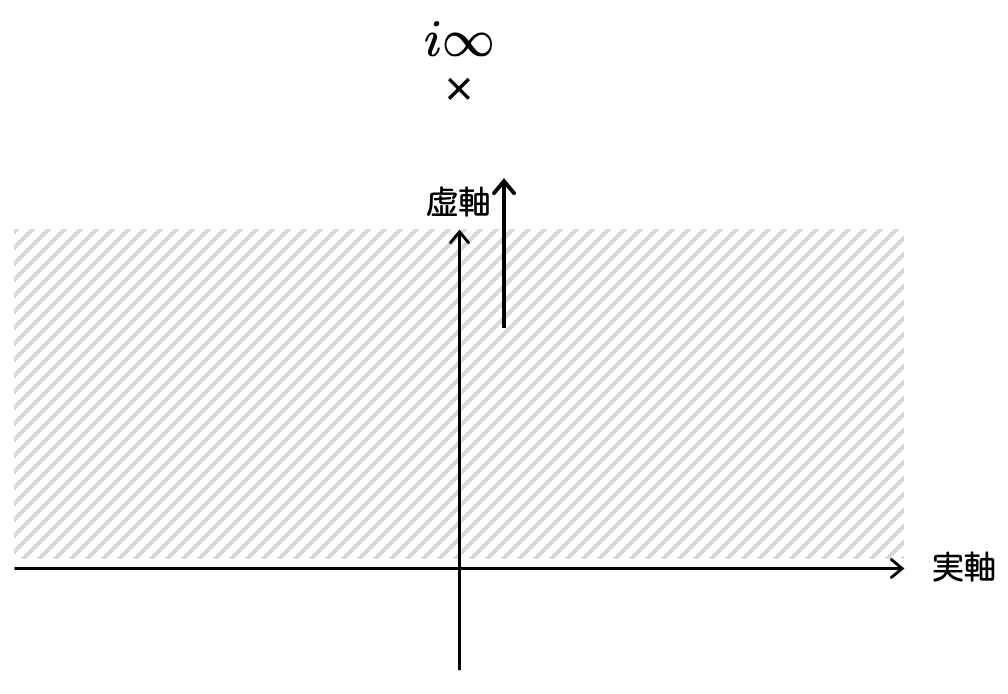
上半平面 $H$ とは、複素数平面のうち虚部が正のもの全体のことです。

$H = \{ z \in \mathbb{C} \; \mid \; \operatorname{Im}(z) > 0 \}$

要するに複素数平面の上半分というわけですね。図に表すとこうなります：

f:id:tsujimotter:20210424230618p:plain:w260

この上半平面上の点 $z\in H$ に対して、 $\operatorname{SL}(2, \mathbb{Z})$ の元 $\gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ による作用が、次のように定義できます：

$\displaystyle \gamma z := \frac{az + b}{cz + d}$

上半平面上の点 $z$ を行列 $\gamma$ によって上半平面上の別の点 $\gamma z$ に写すことができ、そのルールを一次分数変換によって定めたというわけですね。

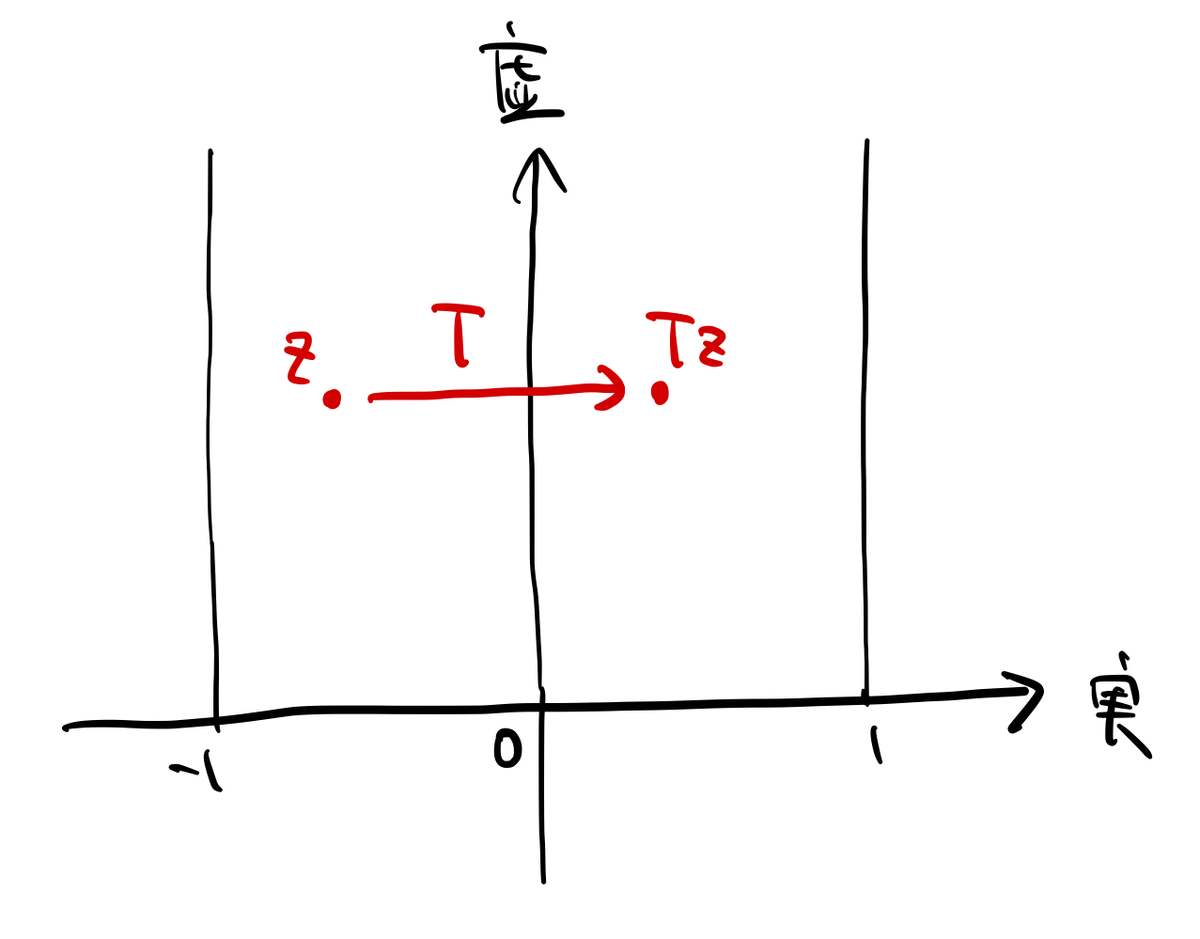
たとえば、 $\operatorname{SL}(2, \mathbb{Z})$ 内の基本的な行列 $T = \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix}$ を考えます。これを $z \in H$ に作用させると

$\displaystyle Tz = \frac{1z + 1}{0z + 1} = z + 1$

となります。これは上半平面上の点を $1$ だけ右方向に移動させる変換になりますね。

f:id:tsujimotter:20210424231635j:plain:w280

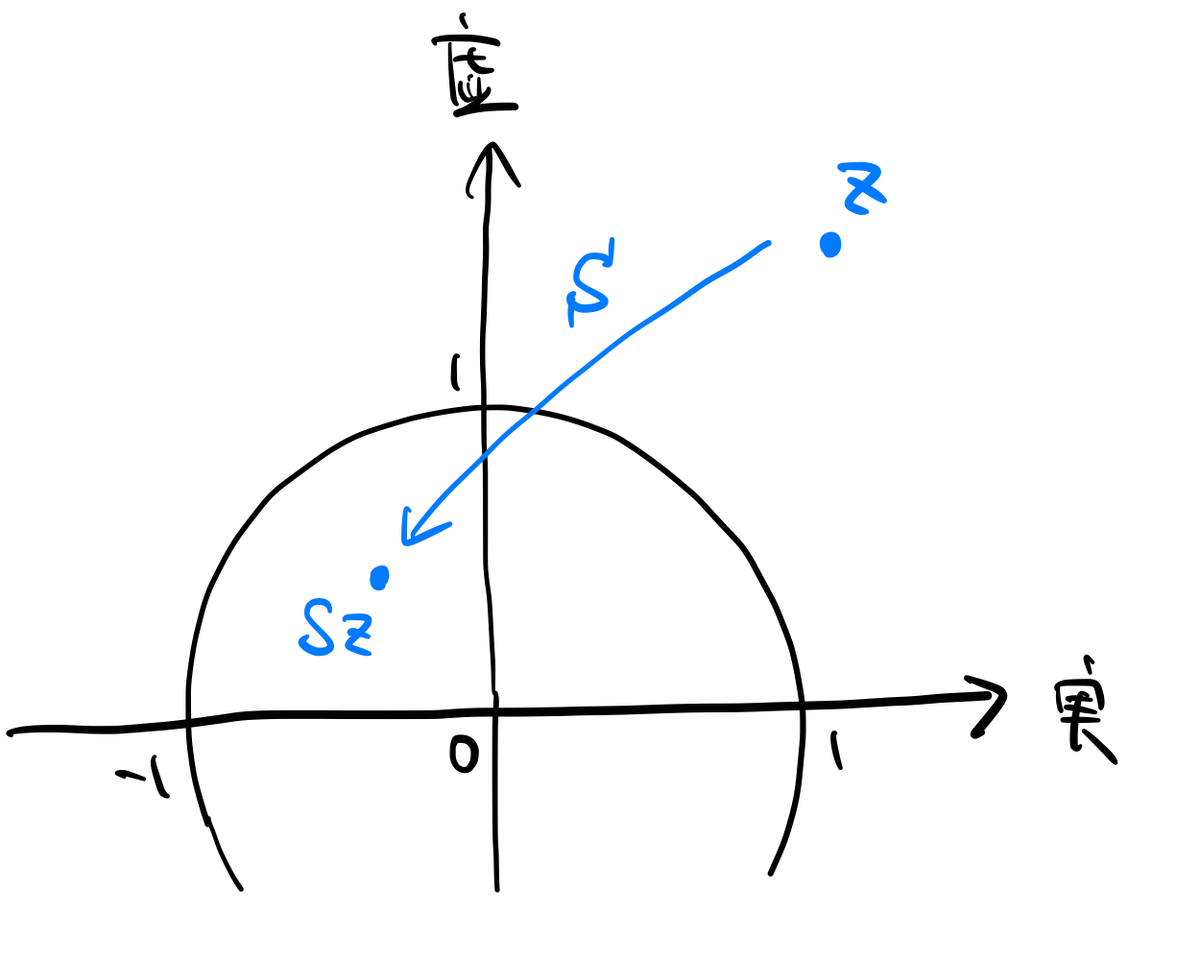
また、もう一つの基本的な行列 $S = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}$ を考えます。これを $z \in H$ に作用させると

$\displaystyle Sz =\frac{0z + 1}{(-1)z + 1} = -\frac{1}{z}$

となります。これは少しイメージしづらいですが、単位円の外の点を中の点へ、中の点を外の点へと写す変換となります。

f:id:tsujimotter:20210424231703j:plain:w280

$S$ と $T$ はあとで何度も出てくる行列なので、ぜひ定義と特性を覚えておいてください。

一般に、行列 $A = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{SL}(2, \mathbb{Z})$ に対して、 $-A$ を考えると

$\displaystyle (-A)z = \frac{(-a)z + (-b)}{(-c)z + (-d)} = \frac{az + b}{cz + d} = Az$

となります。

このことから、単位行列を $I$ としたとき、 $\{ \pm I \}$ によって同一視された $\operatorname{SL}(2, \mathbb{Z})$ の２つの行列 $\pm A$ 同士は、上半平面に同じように作用することになります。つまり、上半平面には $\operatorname{PSL}(2, \mathbb{Z})$ そのものが作用すると考えてもよいわけですね。

そんなわけで、上半平面への作用を考えることで、自然に $\operatorname{PSL}(2, \mathbb{Z})$ が現れます。

続いて、上半平面上の２点 $z, z' \in H$ の間に、ある行列 $\gamma \in \operatorname{SL}(2, \mathbb{Z})$ が存在して

$\gamma z = z'$

が成り立つとき、二項関係 $z \sim z'$ で表すとします。この二項関係 $\sim$ は同値関係となります。

そこで、上半平面 $H$ を同値関係 $\sim$ で割った集合（商集合）を $\operatorname{SL}(2, \mathbb{Z}) \setminus H$ と表すことにします。

これは、 $\operatorname{SL}(2, \mathbb{Z})$ と $H$ の差集合ではなくて、あくまで $H/\sim$ を表したものです。

普通の商集合は $H / \operatorname{SL}(2, \mathbb{Z})$ のように表すことが多いと思いますが、今回は $\operatorname{SL}(2, \mathbb{Z})$ は $H$ に左から作用するので、その作用の向きも合わせて $\operatorname{SL}(2, \mathbb{Z}) \setminus H$ と表すことにします。

なお、紛らわしいので、 $A$ と $B$ の差集合自体は $A - B$ で表すことにします。

上では「 $\operatorname{SL}(2, \mathbb{Z})$ の作用で割る」ということをしていますが、これがなかなか直感的ではありませんね。

$\operatorname{SL}(2, \mathbb{Z}) \setminus H$ は同値類（複数の点を同値関係 $\sim$ で同一視した元の集合）なので、その代表元をとることにすると、比較的イメージしやすくなります。あくまで代表元であるということは意識しつつも、商集合を代表元そのものだと思って議論することは多々あります。

たとえば、 $\mathbb{Z}/n\mathbb{Z}$ の代表元として $\{0, 1, 2, \ldots, n-1\}$ を考え、あたかも $0$ から $n-1$ までの数の足し算だと思うことは整数論ではよくありますが、それと同じようなことです。

特に $\operatorname{SL}(2, \mathbb{Z})$ の「連結な」代表元全体の集合 $\Omega$ を $\operatorname{SL}(2, \mathbb{Z})$ の基本領域といいます。この領域を $\operatorname{SL}(2, \mathbb{Z}) \setminus H$ の代わりに使うことができるわけですね。

$\operatorname{SL}(2, \mathbb{Z})$ の基本領域 $\Omega$ は次のような領域となります：

f:id:tsujimotter:20210424232353p:plain:w360

実際、 $\Omega$ を $\operatorname{SL}(2, \mathbb{Z})$ の元で「ペタペタと」写していくと、 $H$ 全体をもれなく被りなく覆うことができます。

このことを直感的に理解するために、以前「基本領域ゲーム」というのを作ったことがあります。
tsujimotter.info

$\operatorname{SL}(2, \mathbb{Z})$ は、上で書いた３つの行列 $S, T, -I$ によって生成されることが知られています。すなわち、 $\operatorname{SL}(2, \mathbb{Z})$ の任意の元は、 $S, T, -I$ およびそれらの逆元の有限個の積によって表すことができます。また、 $-I$ については、上半平面に恒等的に作用するので、考える必要はありません。 $S, T$ の変換についてのボタンがあれば十分というわけですね。

$S, T$ の組み合わせを $\Omega$ に作用させることで全平面を覆えることを、ゲームを通して体感してみてください！

続いて、 $H$ に無限遠点 $i\infty$ と $\mathbb{Q}$ を加えた拡張された上半平面

$H^* := H \cup \{ i\infty \} \cup \mathbb{Q}$

を考えます。 $\mathbb{Q}$ は実軸上の離散的な点の集合として、 $i\infty$ は虚軸方向のずっと先の極限として考えるイメージです。

f:id:tsujimotter:20210424232532p:plain:w360

$i\infty$ という点は $\operatorname{SL}(2, \mathbb{Z})$ の作用によって、次のような計算により $\mathbb{Q}$ の任意の点に写すことができます。

$\displaystyle \frac{az + b}{cz + d} = \frac{a + b/z}{c + d/z} \xrightarrow{z \to i\infty} \frac{a}{c} \in \mathbb{Q}$

$a, c \in \mathbb{Z}$ は互いに素より、ユークリッドの互除法で $ad - bc = 1$ なる $b, d \in \mathbb{Z}$ がとれる。

したがって、 $H^*$ を $\operatorname{SL}(2, \mathbb{Z})$ で割った商集合 $\operatorname{SL}(2, \mathbb{Z}) \setminus H^*$ は、 $\operatorname{SL}(2, \mathbb{Z}) \setminus H$ に対して $i\infty$ の同値類１点を加えた集合となります：

$\operatorname{SL}(2, \mathbb{Z}) \setminus H^* = (\operatorname{SL}(2, \mathbb{Z}) \setminus H) \cup \{ \overline{i\infty}\}$

$\operatorname{SL}(2, \mathbb{Z}) \setminus H$ と $\operatorname{SL}(2, \mathbb{Z}) \setminus H^*$ のいずれも、適切に位相やアトラスを設定することでリーマン面の構造を持つことが示されます。特に、後者の $\operatorname{SL}(2, \mathbb{Z}) \setminus H^*$ はコンパクトなリーマン面になります。

先ほど $i\infty$ を加えた理由がここにあります。得られるリーマン面をコンパクトにしたかったというわけですね。結果的に、一点 $\overline{i\infty}$ を加えてコンパクト化したことになるので、こういうものを一点コンパクト化といいます。

コンパクト化したリーマン面 $\operatorname{SL}(2, \mathbb{Z}) \setminus H^*$ のことを $\operatorname{SL}(2, \mathbb{Z})$ についてのモジュラー曲線といいます。特に $X(1)$ と書いたりします。

さらに、 $X(1)$ の種数は $0$ であることも知られています。したがって、位相構造だけ見た場合、球面に同相であることも分かります。

直感的に理解した気分になるために、以下の記事で説明を書いたことがあります。ご覧になってください。
tsujimotter.hatenablog.com

難しくてよくわからんという方は、とりあえず $X(1) = \operatorname{SL}(2, \mathbb{Z}) \setminus H^*$ の形は球面だと思えるよと思っていただければ十分です。

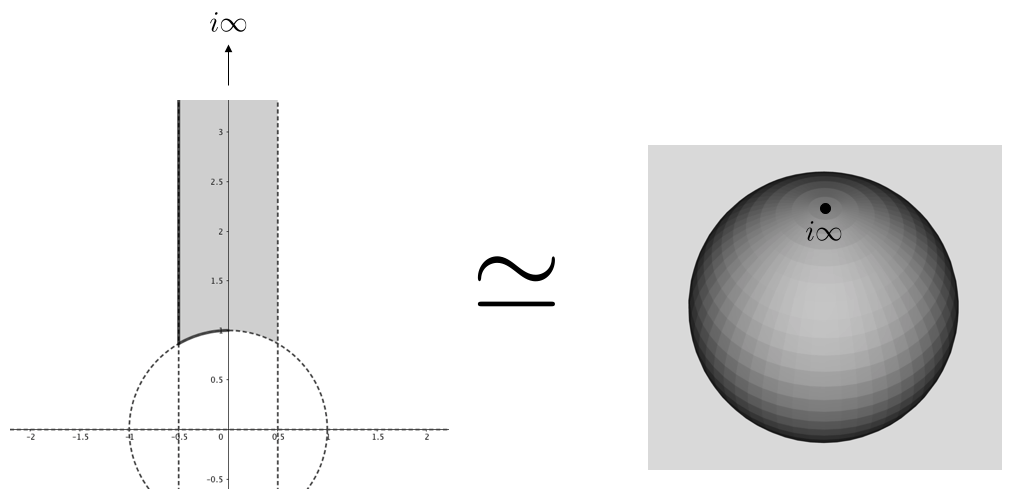
f:id:tsujimotter:20210424232819p:plain:w400

もう一つポアンカレ円板という表現方法を紹介します。これは上半平面の異なる表現方法となります。

上半平面上の点は、ケイリー変換を使って単位円板上の点に写すことができます。上半平面上の任意の点 $z \in H$ に対して定まる

$\displaystyle z \; \longmapsto \; \frac{z-i}{z+i}$

なる変換をケイリー変換といいます。

ケイリー変換によって、上半平面上の点を単位円板に１対１に写すことができるわけです。行き先の単位円板をポアンカレ円板といいます。動画内ではこのポアンカレ円板上で考えているので、以下もポアンカレ円板上で考えたいと思います。
（以降、ケイリー変換を通してポアンカレ円板を上半平面と同一視するので、ポアンカレ円板も同じ記号 $H$ と表すことにします。）

$\operatorname{SL}(2, \mathbb{Z})$ の基本領域 $\Omega$ をケイリー変換によって写すと次のようになります：

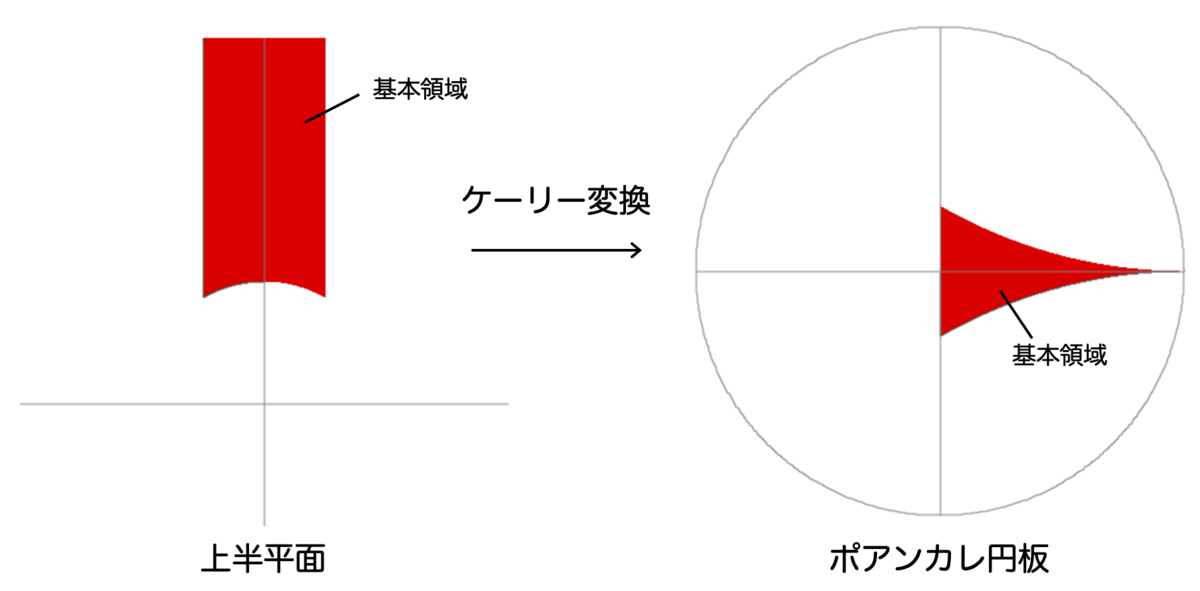
f:id:tsujimotter:20210425222108p:plain:w480

上半平面上のカスプ $i\infty$ は、ポアンカレ円板の単位円上の $z = 1$ の点に対応することを覚えておいてください。また、ポアンカレ円板の単位円の境界にある点は、上半平面における $i\infty$ か $\mathbb{Q}$ のいずれかの点に対応します。

ポアンカレ円板上にも、上半平面と同じように $\operatorname{SL}(2, \mathbb{Z})$ の作用を考えることができます。この作用のイメージを理解するために、ポアンカレ円板バージョンの基本領域ゲームを作ってみましたので、ぜひ体感してみてください。
tsujimotter.info

モジュラー曲線 $X(5)$ と $\operatorname{PSL}(2, \mathbb{F}_5)$ の作用

今回の話では、上記のモジュラー曲線 $X(1) = \operatorname{SL}(2, \mathbb{Z}) \setminus H^*$ の代わりに、 $\Gamma(5)$ のモジュラー曲線 $X(5) = \Gamma(5) \setminus H^*$ を考える必要があります。（後ほど定義します。）

先ほどは、上半平面（あるいはポアンカレ円板） $H$ に $\operatorname{SL}(2, \mathbb{Z})$ を作用させたわけですが、今度は $\operatorname{SL}(2, \mathbb{Z})$ の部分群の一つである $\Gamma(5)$ という群を作用させます。

$\Gamma(5)$ の定義は次の通りです：

$\displaystyle \Gamma(5) := \left\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{SL}(2, \mathbb{Z}) \; \middle| \; \begin{pmatrix} a & b \\ c & d \end{pmatrix} \equiv \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \pmod{5} \right\}$

これがいったいどんな群であるのかは後で述べたいと思います。

先ほどと同じように、 $H$ や $H^*$ を $\Gamma(5)$ で割ってできる商集合 $\Gamma(5) \setminus H, \;\; \Gamma(5) \setminus H^*$ を考えましょう。

ポイントになるのは $H$ に作用させる群 $\Gamma(5)$ が、元々の $\operatorname{SL}(2, \mathbb{Z})$ の部分群であり、つまり「より小さい群」になっているという点です。 $\Gamma(5)$ で同一視される点の集合が小さくなるので、 $\Gamma(5)$ の基本領域 $\Omega(5)$ は逆に広くなるわけです。

実際、 $\Omega(5)$ を描くと次のようになります：

f:id:tsujimotter:20210424203442p:plain:w360

まず、 $\Omega(5)$ は $\operatorname{SL}(2, \mathbb{Z})$ の基本領域 $\Omega$ の $60$ 個分のタイリングによって構成されています。（なぜ $60$ になるかについては、後ほどじっくり説明します。）

この基本領域は自分の力で書いたものですが、元々の動画の基本領域とは微妙に異なります。おそらく動画の方は黒い領域のいくつかを忘れているように思うのですが・・・。

$\Omega(5)$ を構成する各タイルは、 $\Omega$ 以外のものについては「 $\operatorname{SL}(2, \mathbb{Z})$ によっては同一視されるが、 $\Gamma(5)$ では同一視されないタイル」ということになります。

つまり、 $\operatorname{SL}(2, \mathbb{Z}) / \Gamma(5)$ （正確には $\operatorname{PSL}(2, \mathbb{Z}) / \Gamma(5)$ ）の代表元 $\gamma_1, \ldots, \gamma_{60}$ を適切に選ぶことによって、 $\Omega(5)$ を $\gamma_1 \Omega, \ldots, \gamma_{60} \Omega$ の和集合として表せるわけです。

実際、上で描画した基本領域 $\Omega(5)$ の各タイルは、次の $60$ 個の行列を $\Omega$ に作用させることによって生成されます。行列は基本領域に塗られた色ごとに別々の行として表現しています：

（右の赤） $\begin{pmatrix}1 & -2 \\ 0 & 1 \end{pmatrix}, \begin{pmatrix}1 & -1 \\ 0 & 1 \end{pmatrix}, \begin{pmatrix}1 & 0 \\ 0 & 1 \end{pmatrix}, \begin{pmatrix}1 & 1 \\ 0 & 1 \end{pmatrix}, \begin{pmatrix}1 & 2 \\ 0 & 1 \end{pmatrix},$
（左の黄） $\begin{pmatrix}0 & -1 \\ 1 & -2 \end{pmatrix}, \begin{pmatrix}0 & -1 \\ 1 & -1 \end{pmatrix}, \begin{pmatrix}0 & -1 \\ 1 & 0 \end{pmatrix}, \begin{pmatrix}0 & -1 \\ 1 & 1 \end{pmatrix}, \begin{pmatrix}0 & -1 \\ 1 & 2 \end{pmatrix},$
（上の青） $\begin{pmatrix}1 & -3 \\ 1 & -2 \end{pmatrix}, \begin{pmatrix}1 & -2 \\ 1 & -1 \end{pmatrix}, \begin{pmatrix}1 & -1 \\ 1 & 0 \end{pmatrix}, \begin{pmatrix}1 & 0 \\ 1 & 1 \end{pmatrix}, \begin{pmatrix}1 & 1 \\ 1 & 2 \end{pmatrix},$
（下の緑） $\begin{pmatrix}-1 & 2 \\ 1 & -3 \end{pmatrix}, \begin{pmatrix}-1 & 1 \\ 1 & -2 \end{pmatrix}, \begin{pmatrix}-1 & 0 \\ 1 & -1 \end{pmatrix}, \begin{pmatrix}-1 & -1 \\ 1 & 0 \end{pmatrix}, \begin{pmatrix}-1 & -2 \\ 1 & 1 \end{pmatrix},$
（右下の黒） $\begin{pmatrix}-2 & 3 \\ 1 & -2 \end{pmatrix}, \begin{pmatrix}-2 & 1 \\ 1 & -1 \end{pmatrix}, \begin{pmatrix}-2 & -1 \\ 1 & 0 \end{pmatrix}, \begin{pmatrix}-2 & -3 \\ 1 & 1 \end{pmatrix}, \begin{pmatrix}-2 & -5 \\ 1 & 2 \end{pmatrix},$
（左下の赤） $\begin{pmatrix}-2 & 7 \\ 3 & -11 \end{pmatrix}, \begin{pmatrix}-2 & 5 \\ 3 & -8 \end{pmatrix}, \begin{pmatrix}-2 & 3 \\ 3 & -5 \end{pmatrix}, \begin{pmatrix}-2 & 1 \\ 3 & -2 \end{pmatrix}, \begin{pmatrix}-2 & -1 \\ 3 & 1 \end{pmatrix},$
（右上の黄） $\begin{pmatrix}-3 & 8 \\ -2 & 5 \end{pmatrix}, \begin{pmatrix}-3 & 5 \\ -2 & 3 \end{pmatrix}, \begin{pmatrix}-3 & 2 \\ -2 & 1 \end{pmatrix}, \begin{pmatrix}-3 & -1 \\ -2 & -1 \end{pmatrix}, \begin{pmatrix}-3 & -4 \\ -2 & -3 \end{pmatrix},$
（左下の青） $\begin{pmatrix}1 & 0 \\ -2 & 1 \end{pmatrix}, \begin{pmatrix}1 & 1 \\ -2 & -1 \end{pmatrix}, \begin{pmatrix}1 & 2 \\ -2 & -3 \end{pmatrix}, \begin{pmatrix}1 & 3 \\ -2 & -5 \end{pmatrix}, \begin{pmatrix}1 & 4 \\ -2 & -7 \end{pmatrix},$
（右上の緑） $\begin{pmatrix}2 & -1 \\ 1 & 0 \end{pmatrix}, \begin{pmatrix}2 & 1 \\ 1 & 1 \end{pmatrix}, \begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix}, \begin{pmatrix}2 & 5 \\ 1 & 3 \end{pmatrix}, \begin{pmatrix}2 & 7 \\ 1 & 4 \end{pmatrix},$
（左上の黒） $\begin{pmatrix}-1 & 2 \\ -2 & 3 \end{pmatrix}, \begin{pmatrix}-1 & 1 \\ -2 & 1 \end{pmatrix}, \begin{pmatrix}-1 & 0 \\ -2 & -1 \end{pmatrix}, \begin{pmatrix}-1 & -1 \\ -2 & -3 \end{pmatrix}, \begin{pmatrix}-1 & -2 \\ -2 & -5 \end{pmatrix},$
（右上の赤） $\begin{pmatrix}5 & -2 \\ 3 & -1 \end{pmatrix}, \begin{pmatrix}5 & 3 \\ 3 & 2 \end{pmatrix}, \begin{pmatrix}5 & 8 \\ 3 & 5 \end{pmatrix}, \begin{pmatrix}5 & 13 \\ 3 & 8 \end{pmatrix}, \begin{pmatrix}5 & 18 \\ 3 & 11 \end{pmatrix},$
（左下の黄） $\begin{pmatrix}-3 & 4 \\ 5 & -7 \end{pmatrix}, \begin{pmatrix}-3 & 1 \\ 5 & -2 \end{pmatrix}, \begin{pmatrix}-3 & -2 \\ 5 & 3 \end{pmatrix}, \begin{pmatrix}-3 & -5 \\ 5 & 8 \end{pmatrix}, \begin{pmatrix}-3 & -8 \\ 5 & 13 \end{pmatrix}$

参考までに、上記の行列は次の要領で得られました。

まず、基準となる12個の行列

$\begin{pmatrix}1 & 0 \\ 0 & 1 \end{pmatrix}, \begin{pmatrix}0 & -1 \\ 1 & 0 \end{pmatrix}, \begin{pmatrix}1 & -1 \\ 1 & 0 \end{pmatrix}, \begin{pmatrix}-1 & 0 \\ 1 & -1 \end{pmatrix}, \begin{pmatrix}-2 & -1 \\ 1 & 0 \end{pmatrix}, \begin{pmatrix}-2 & 3 \\ 3 & -5 \end{pmatrix},$
$\begin{pmatrix}-3 & 2 \\ -2 & 1 \end{pmatrix}, \begin{pmatrix}1 & 2 \\ -2 & -3 \end{pmatrix}, \begin{pmatrix}2 & 3 \\ 1 & 2 \end{pmatrix}, \begin{pmatrix}-1 & 0 \\ -2 & -1 \end{pmatrix}, \begin{pmatrix}5 & 8 \\ 3 & 5 \end{pmatrix}, \begin{pmatrix}-3 & -2 \\ 5 & 3 \end{pmatrix}$

を用意します。これを $\Omega$ に作用させると次のようなタイルが得られます：

f:id:tsujimotter:20210425162923p:plain:w240

この12個の行列に1行目の行列を右からかけると、前述の60個の行列が得られます。つまり、作用の順番としては、1行目の行列を作用させたあと、上記の12個の行列を作用させるということですね。

$\operatorname{SL}(2, \mathbb{Z}) / \Gamma(5)$ の相異なる元であることを確認するために、

どれも $\operatorname{det}\gamma_i = 1$ であること
$i \neq j$ のとき $\gamma_i \gamma_j^{-1} \not\in \Gamma(5)$ であること

については検証済みです。

特に、1行目にある5つの行列は、 $\operatorname{SL}(2, \mathbb{Z}) / \Gamma(5)$ の部分群をなします。この部分群

$\displaystyle \langle T \rangle = \left\{ T^{-2}, T^{-1}, I, T, T^2 \right\}$

は5次の巡回群（ $5$ 回で一周する）となります。 $\gamma \in \langle T \rangle$ を使って $\Omega$ を写した領域 $\gamma\Omega$ は $\Omega$ と同じ $i\infty$ のカスプと接するタイルです。これらの和集合

$T^{-2}\Omega \cup T^{-1}\Omega \cup \Omega \cup T^{1}\Omega \cup T^{2}\Omega$

は、下の図のように繋がることを考慮に入れると、 $i\infty$ を内部に含むような正五角形（下図の右）となります。

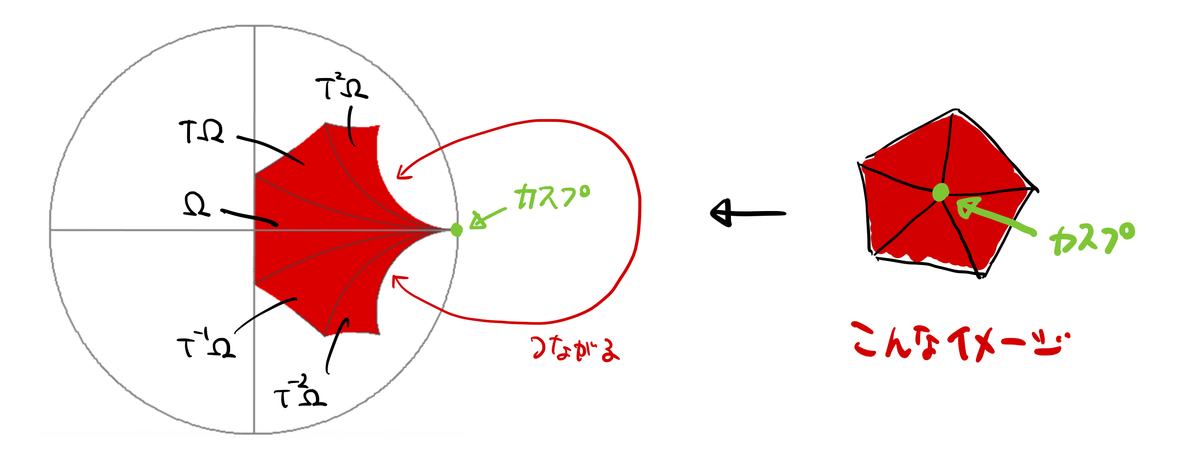
f:id:tsujimotter:20210425013527j:plain:w500

ここで「 $\Gamma(5)$ は $\Gamma$ の $60$ 個のタイリングである」ということについて、理屈を説明をしましょう。

$\operatorname{SL}(2, \mathbb{Z})$ の任意の行列に対し「行列の係数を $\bmod{5}$ する写像」を考えることができます。これを $\pi$ とすると、 $\pi$ は $\operatorname{SL}(2, \mathbb{F}_5)$ への全射準同型となっています：

$\pi\; \colon \operatorname{SL}(2, \mathbb{Z}) \; \twoheadrightarrow \; \operatorname{SL}(2, \mathbb{F}_5)$

ここで、 $\Gamma(5)$ の定義から $\operatorname{ker}( \pi ) = \Gamma(5)$ であることがわかります。これが $\Gamma(5)$ の正体だったわけですね。

準同型定理により、群の同型

$\operatorname{SL}(2, \mathbb{Z}) \big/ \Gamma(5) \; \simeq \; \operatorname{SL}(2, \mathbb{F}_5)$

が得られます。

$\pi\colon \operatorname{SL}(2, \mathbb{Z}) \; \twoheadrightarrow \; \operatorname{SL}(2, \mathbb{F}_5)$ に対して、 $\pm I$ で割ることによって、 $\operatorname{PSL}$ に対する同様の全射準同型

$\tilde{\pi}\; \colon \operatorname{PSL}(2, \mathbb{Z}) \; \twoheadrightarrow \; \operatorname{PSL}(2, \mathbb{F}_5)$

が得られます。この核はやはり $\Gamma(5)$ となります。よって、準同型定理より群の同型

$\operatorname{PSL}(2, \mathbb{Z}) \big/ \Gamma(5) \; \simeq \; \operatorname{PSL}(2, \mathbb{F}_5)$

が得られます。

したがって、 $\Gamma(5)$ の基本領域 $\Omega(5)$ は、 $\Gamma$ の $\operatorname{PSL}(2, \mathbb{F}_5)$ の元に対応する $\Omega$ のタイリングで生成されるということになります。 $\operatorname{PSL}(2, \mathbb{F}_5)$ の位数を計算すれば良いわけですね。

ここで、 $\operatorname{PSL}(2, \mathbb{F}_5)$ の位数には

$\displaystyle \# \operatorname{PSL}(n, \mathbb{F}_q) = q^{n(n-1)/2}\prod_{i=2}^n \frac{q^i - 1}{\operatorname{gcd}(n, q-1)}$

という一般的な公式があります。

$n = 2, \; q = 5$ として計算すると

$\displaystyle \# \operatorname{PSL}(2, \mathbb{F}_5) = 5^{2(2-1)/2}\prod_{i=2}^2 \frac{5^i - 1}{\operatorname{gcd}(2, 5-1)} = 5\cdot \frac{5^2-1}{2} = 60$

となります。ちゃんと $60$ が出てきましたね！

そんなわけで、 $\Omega(5)$ が $\Omega$ の60個のタイリングであることがわかるわけです！

$\Gamma(5)$ に対しても、 $\operatorname{SL}(2, \mathbb{Z})$ と同じ要領でモジュラー曲線を考えることができます。

$\Gamma(5) \setminus H, \; \Gamma(5) \setminus H^*$ にはリーマン面の構造が入ります。（これも難しいので詳細は述べれませんが。）

特に、後者の $\Gamma(5) \setminus H^*$ はコンパクトなリーマン面となります。この $\Gamma(5) \setminus H^*$ を $\Gamma(5)$ についてのモジュラー曲線といい、 $X(5)$ で表すことにします。

ここで、 $\Gamma(5)$ のカスプは

$\Gamma(5) \setminus H^* - \Gamma(5) \setminus H$

ということになりますが、これは $12$ 点の集合になります。 $\operatorname{SL}(2, \mathbb{Z})$ よりも同一視する点が減るので、その分カスプが増えるわけですね。

実際、 $\Omega(5)$ に $12$ 点のカスプを描画すると次のようになります：

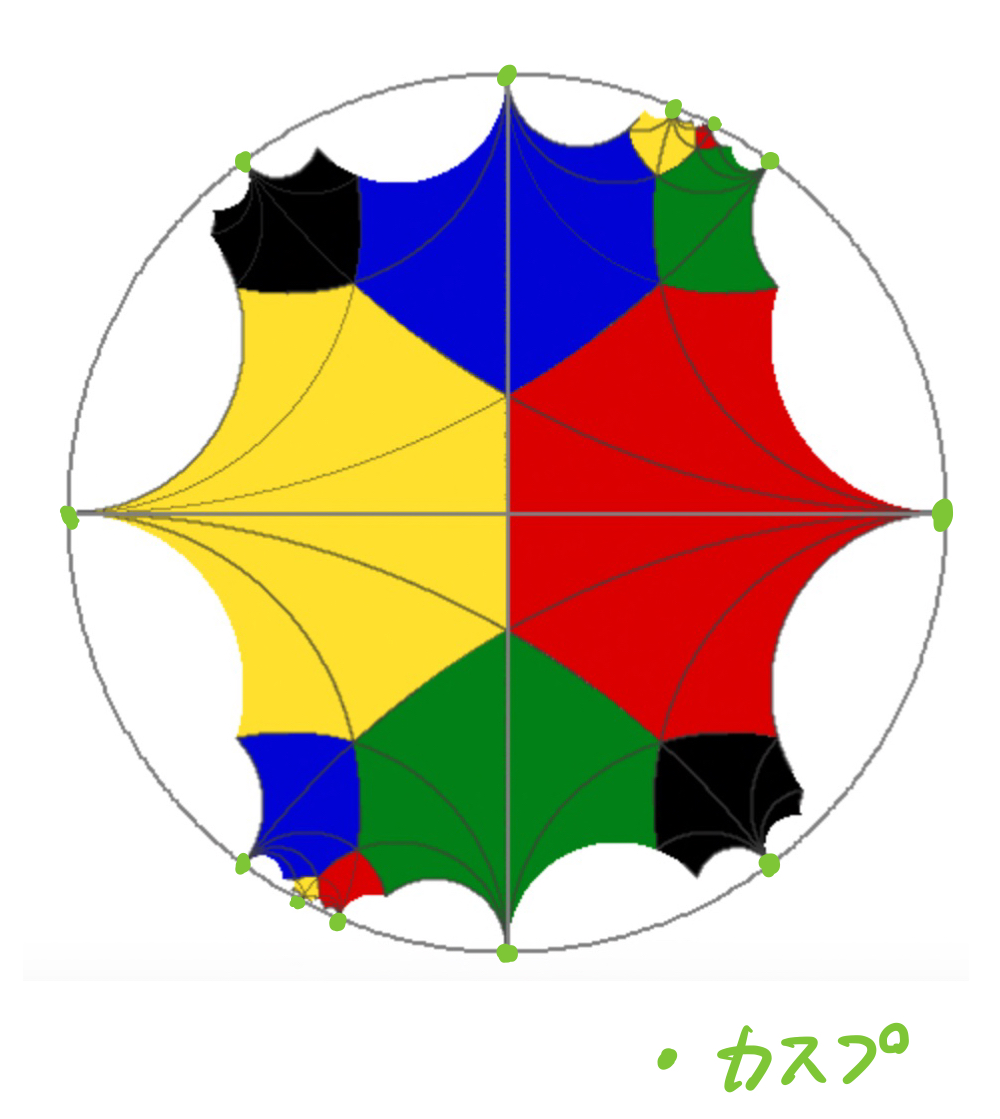
f:id:tsujimotter:20210424212748j:plain:w300

コンパクトリーマン面 $X(5)$ は一体どのようなリーマン面なのか、考えてみたいと思います。コンパクトリーマン面というのがミソで、種数によって分類することができるわけです。

$\operatorname{SL}(2, \mathbb{Z})$ による同値関係を $\sim$ とすると、 $X(1) = X(5)/\sim$ なので $X(5)$ から $X(1)$ への商写像を考えることができます。これがリーマン面の間の全射正則写像になります。つまり、リーマン面の $60$ 次の被覆写像が得られたわけですね。

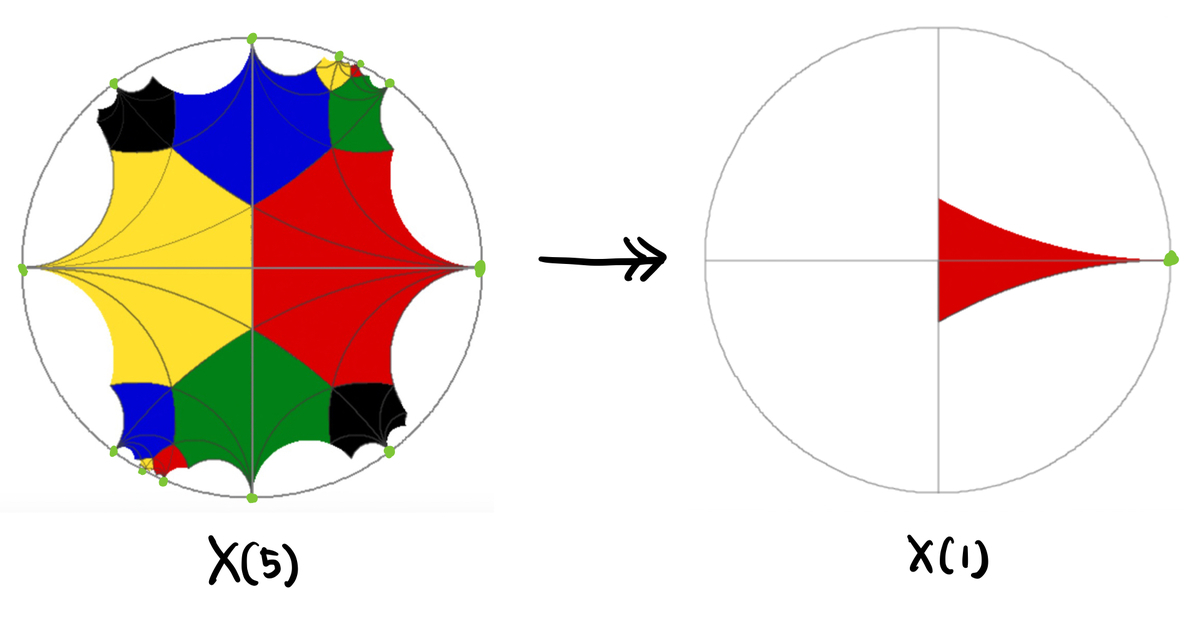
f:id:tsujimotter:20210425024837j:plain:w400

ここでリーマン・フルヴィッツの公式を使うと、 $X(5)$ の種数を計算できます。この辺の計算をちゃんと理解できていないのですが、"A First Course in Modular Forms" の計算を信じることにしたいと思います。

素数 $p > 2$ についてのモジュラー曲線 $X(p)$ の種数公式

$\displaystyle g = 1 + \frac{(p^2 - 1)(p - 6)}{24}$

を用いると、 $p = 5$ より

$\displaystyle g = 1 + \frac{(5^2 - 1)(5 - 6)}{24} = 1 - 1 = 0$

となり、 $g = 0$ がわかります。

すなわち、種数 $0$ のコンパクトリーマン面ということが分かりましたので、位相構造としては $X(5)$ は球面に同相であるというわけです。形だけ見れば、球面だと思って良いわけですね。

実際、連結性に気をつけながら $X(5)$ を球面上に表すと、次のようになります：

f:id:tsujimotter:20210425123048j:plain:w240

球面に $\Omega$ をコピーしたタイルが $60$ 個張り付いていますが、これは球面の「三角形分割」を与えていると思うことができますね。

色の対応が公式と異なると思ったかたは鋭い方です。私の認識が間違っていなければ、たぶん公式の色の塗りかたの方が間違っているかと思います。

この球面に対して $\operatorname{PSL}(2, \mathbb{F}_5) \simeq \operatorname{PSL}(2, \mathbb{Z}) / \Gamma(5)$ が、三角形のタイルの形や位置関係を保つように作用していると考えることができます。

これはリーマン面の被覆

$f\colon X(5) \twoheadrightarrow X(1)$

の観点で言うと、 $X(5)$ の自己同型写像 $g\colon X(5) \longrightarrow X(5)$ であって $f\circ g = f$ を満たすようなものとなっています。このような $g$ のなす群を被覆変換群というそうです。

したがって、 $\operatorname{PSL}(2, \mathbb{F}_5)$ は被覆 $X(5) \twoheadrightarrow X(1)$ の被覆変換群であるというわけですね。

具体的な変換の仕方は、次のようになります。たとえば行列 $T$ は、手前の赤い五角形を右に $1/5$ 回転させるような変換となります。ポアンカレ円板上では $T$ は次のような変換に相当します：

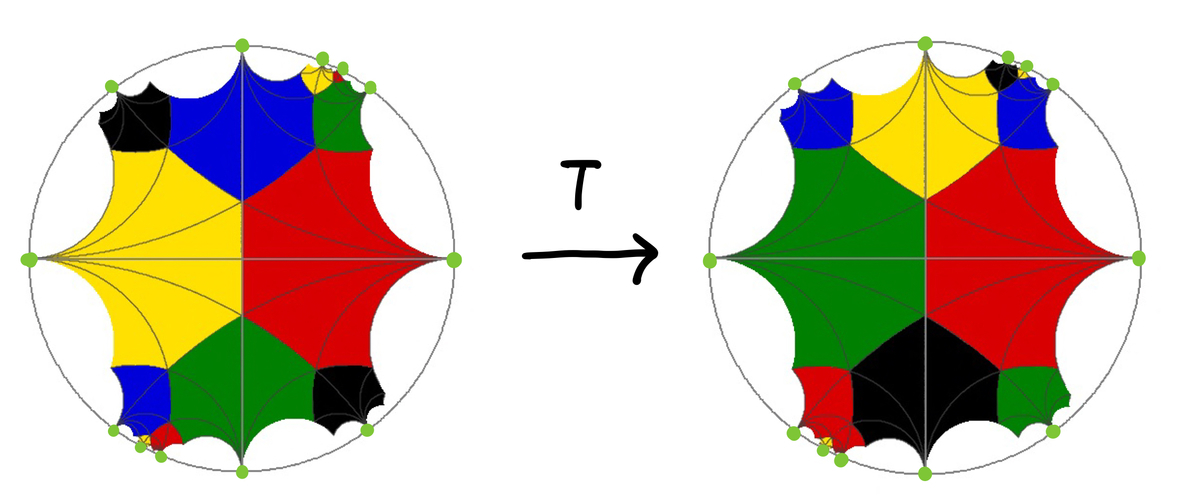
f:id:tsujimotter:20210425162101j:plain:w460

カスプに着目すると、 $\Gamma(5)$ のカスプは $12$ 点あるわけですが、 $\operatorname{PSL}(2, \mathbb{F}_5)$ の任意の元はこれらの $12$ 点のカスプの間の置換に対応することになります。

変換の様子を確認するページも作りましたので、よかったら遊んでみてください：
tsujimotter.info

$\operatorname{PSL}(2, \mathbb{F}_5)$ と $A_5$ の関係

ここまで考えると、正十二面体群との関係が見えてくると思います。

正十二面体の頂点に外接する球面を考えて、正十二面体の辺・面を膨らませるとこうなります。

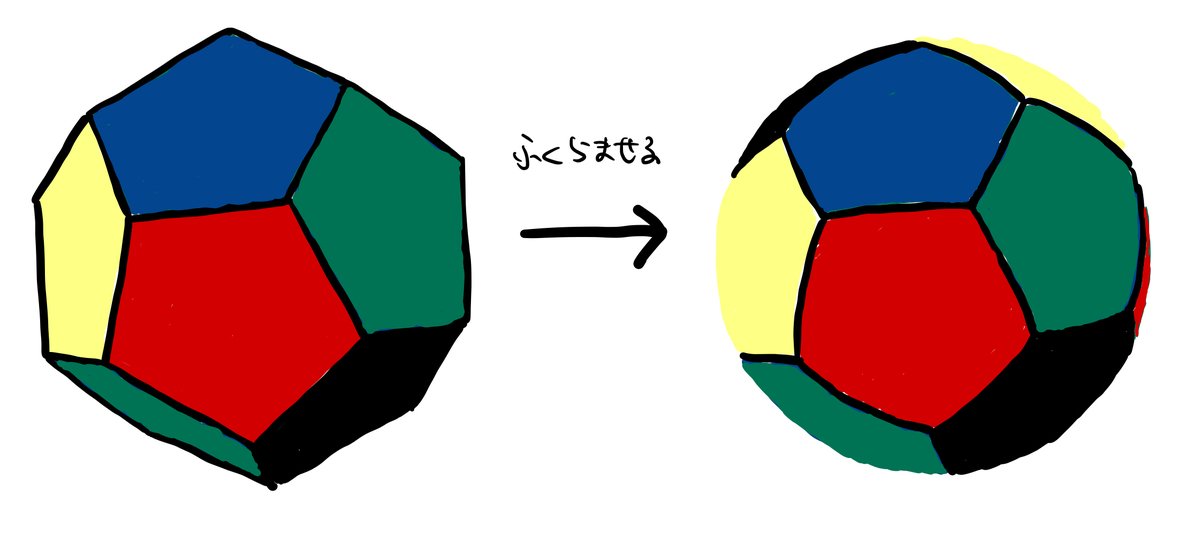
f:id:tsujimotter:20210425124657j:plain:w400

これが先ほどのモジュラー曲線 $X(5)$ のリーマン球面と対応するのがわかるでしょう。 $\Gamma(5)$ の基本領域 $\Omega(5)$ は、ポアンカレ円板上の展開図だったのですね。

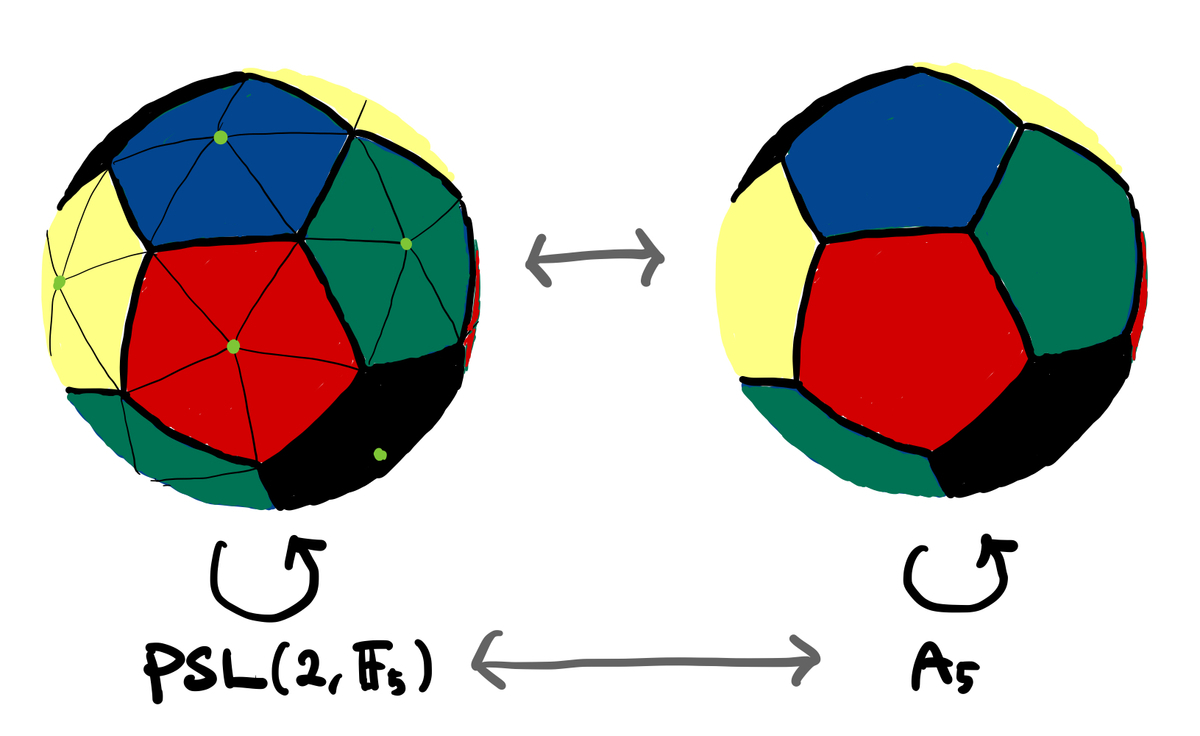
f:id:tsujimotter:20210425124720j:plain:w400

$\operatorname{PSL}(2, \mathbb{F}_5)$ のモジュラー曲線 $X(5)$ への作用（被覆変換群）は、 $A_5$ の正十二面体への作用とちょうど対応します。特に $12$ 点のカスプの置換は、 $12$ 個の面の置換に対応するわけです。

こんな風に、 $\operatorname{PSL}(2, \mathbb{F}_5)$ と $A_5$ の間の同型が、直感的に理解できるというわけです。

いやー、面白いですね！

$\operatorname{PSL}(2, \mathbb{F}_3)$ と $\operatorname{PSL}(2, \mathbb{F}_7)$

$\operatorname{PSL}(2, \mathbb{F}_5)$ について考えましたので、この考えを延長して、たとえば $\operatorname{PSL}(2, \mathbb{F}_3)$ や $\operatorname{PSL}(2, \mathbb{F}_7)$ のような群の構造について考えることはできるでしょうか。

まずは $\operatorname{PSL}(2, \mathbb{F}_3)$ から。位数を考えると $\#\operatorname{PSL}(2, \mathbb{F}_3) = 12$ であることが分かります。

$\Gamma(3)$ についてのモジュラー曲線 $X(3) = \Gamma(3) \setminus H^*$ の基本領域を計算すると、次のように $\Omega$ の12個のタイリングで表されます：

f:id:tsujimotter:20210425170105p:plain:w240

$X(3)$ の種数を計算すると、 $g = 0$ であることがわかり、これは位相空間として球面に同相ということになります。基本領域の連結性に着目して、球面にマッピングすると、これは膨らませた正四面体になります。したがって、 $\operatorname{PSL}(2, \mathbb{F}_3)$ は正四面体群に同型であることがわかります。

一般に $\operatorname{PSL}(2, \mathbb{F}_p)$ に対しても、いつでも正多面体群に対応づけられるかというとそうではありません。早速、 $p = 7$ でうまくいきません。

$\operatorname{PSL}(2, \mathbb{F}_7)$ に対応するモジュラー曲線 $X(7)$ は、種数を計算すると $g = 3$ となります。したがって、位相空間としては穴が3つ空いた閉曲面に同相ということになります。「プレッツェル」みたいな形の図形ですね。

f:id:tsujimotter:20161013063837j:plain:w200

プレッツェルのイメージ

プレッツェルの表面に七角形が $24$ 個タイリングされたような図形となります。（可視化すると次のリンク先のアニメーションのようになるのではないかと思います。）
math.ucr.edu

$\operatorname{PSL}(2, \mathbb{F}_p)$ は $X(7)$ に自然に作用することはわかります。が、しかし球面ではないため、 $\operatorname{PSL}(2, \mathbb{F}_3)$ や $\operatorname{PSL}(2, \mathbb{F}_5)$ のときのように正多面体群へと対応させることはできなさそうです。

なお、 $\operatorname{PSL}(2, \mathbb{F}_7)$ は位数 $168$ の群なのですが、 $A_5$ の位数 $60$ に次ぐ、二番目に小さな位数を持つ非可換単純群の例として知られていますね。