カレンダーの上の素数〜素数には毎年出会えるか？〜

日曜数学 Advent Calendar 2021 の最終日の記事です。

今日は日曜数学 Advent Calendar 2021 の最終日の記事です。

そんなわけで、12月1日から始まった日曜数学アドベントカレンダーも、今日で終わりです！

おかげさまで、なんと25日間すべての記事が埋まりました！　投稿してくださったみなさま本当にありがとうございます！！

f:id:tsujimotter:20211225213127p:plain:w380

色々なタイプの記事が揃いましたが、今年はMathlogさんからの投稿が7件もありました！勢いを感じますね！

まだ読んでいない方もおられると思いますが、楽しい記事が集まっていますので、ぜひじっくり読んでいただければと思います。
adventar.org

今日のテーマ

突然ですが、私は素数が大好きです。

日常生活においても、たとえば素数の番号のロッカーに荷物を預けますし、レシートの金額が素数だったら喜びます。

当然、今日の日付が素数だったら喜びます。

残念ながら、８桁の数

20211225

は明らかに5の倍数です。つまり素数ではありません。

こんな風に今日の記事では、日付の西暦・月・日を並べて作った数が素数であるかを考えたいと思います。

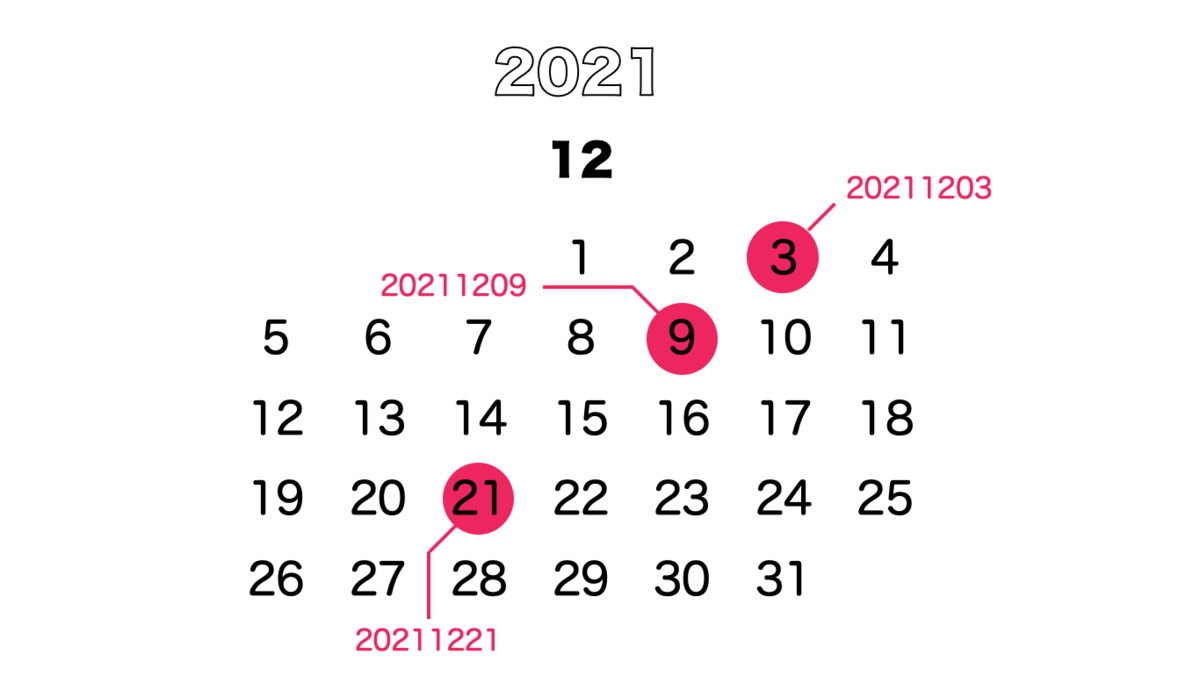
f:id:tsujimotter:20211225213407p:plain:w480

今年2021年には、実は 21日も素数の日があって、以下は素数でした。

20210101,
20210107,
20210131,
20210317,
20210401,
20210503,
20210513,
20210609,
20210717,
20210803,
20210831,
20210923,
20210929,
20211001,
20211007,
20211031,
20211109,
20211127,
20211203,
20211209,
20211221

めでたいですね！

21個ということは、だいたい1月あたり1日超の素数があったことになります。今月は3つもあるので、よい月でしたね！
（2月はなかったみたいですね。）

さて、本題はここからなのですが・・・。

今年は無事素数の日が存在しました。一方で、来年もちゃんと素数の日はあるのでしょうか？

もし一年間素数の日が存在しない年があったとしたら・・・と考えると、苦しくて夜しか眠れませんね。

そんなわけで、毎年素数の日は存在するか？を調べてみたいと思います！

2022年は素数の日があります！

素数ファンの皆さま、おめでとうございます！　来年2022年もちゃんと素数はあります！

全部で23個でした。

20220103, 20220119, 20220121, 20220127, 20220217, 20220307, 20220311, 20220323, 20220331, 20220407, 20220517, 20220601, 20220619, 20220713, 20220817, 20220821, 20220901, 20220923, 20221009, 20221027, 20221127, 20221213, 20221231

2021年は毎月素数があるみたいですね！

今のうちに2021年のカレンダーの日付のところに印をつけておきましょう！

西暦3000年まではどうだろうか？

来年は素数の日があることで一安心ですが、この先はどうでしょうか。

西暦3000年ぐらいまで調べておけば、ちょっと長生きしたとしても大丈夫そうですね。

ところで、調べ方について少し補足したいと思います。

基本的には各年 YYYY0101 〜 YYYY1231 までの数を考えて（YYYYには西暦が入ります）、これらを素数判定して各年ごとに個数を数えます。

細かいですが、うるう年だけ気をつける必要があるので、次のようなルールで計算します。

1. 西暦年が4で割り切れる年は(原則として)閏年。
2. ただし、西暦年が100で割り切れる年は(原則として)平年。
3. ただし、西暦年が400で割り切れる年は必ず閏年。

Pythonプラグラムで書くと、以下のようになります。

def is_leap_year(y):
    if y % 400 == 0:
        return True
    elif y % 100 == 0:
        return False
    elif y % 4 == 0:
        return True
    else:
        return False

また、素数判定については、30000000以下の数について「エラトステネスのふるい」を実行し、この結果を使いました。したがって、素数の個数は厳密に正しいものです。

そんなわけで、結果として得られたグラフがこちらです！

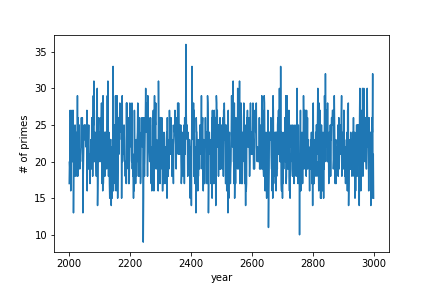
f:id:tsujimotter:20211225200324p:plain:w500

横軸が西暦で、縦軸が各年の素数の日の個数となります。

結果を見る限りでは、素数の日の個数は20〜25個程度で、少ない年でも9個はあるということです。安心して素数ライフが送れそうですね！

確率的に考えてみよう：素数定理

せっかくなので、もう少し数学的に分析をして、3000年といわず、今後もどうなっていくのかを予測してみましょう。

このような問題を考えるにあたって、素数定理が基本です。素数定理によれば、十分大きな $x$ において、 $x$ 以下の素数の個数 $\pi(x)$ は $x/\log x$ に漸近するのでした。すなわち

$\displaystyle \pi(x) \sim \frac{x}{\log x} \tag{1}$

が成り立つということでした。

これはつまり、ある $x$ の周辺において「だいたい $\log x$ 個に1個が素数である」ということを意味します。

素数定理については、次の記事で詳しく説明していますので、興味がある方はどうぞ：
tsujimotter.hatenablog.com

今回は、だいたい $x = 20000000$ の周辺を考えていますので

$\log(20000000) \fallingdotseq 16.8$ 個に1個が素数

ということになります。

カレンダーにある日付の個数はほぼ $365$ 個なので

$\displaystyle \frac{365}{16.8} \fallingdotseq 21.72 \tag{2}$

より、年間の素数の日の個数の期待値は約 $21.72$ 個ということが結論づけられます。

たしかに、これは実際の西暦2000〜3000年の結果とも一致していますね。
（というか、このレベルの話も素数定理でかなりいい精度で見積れるのが面白いですね。）

これを応用すると、いつ素数がなくなる年が訪れるかを見積もることができそうです。

すなわち、調べたい西暦を $y$ 年とすると、この年は $\log(10000y)$ 個に1個が素数になります。したがって、365日間の素数の個数の期待値は

$\displaystyle \frac{365}{\log(10000y)} \tag{3}$

ということになります。

これが $1$ を下回るときは、素数の個数の期待値が1個未満ということになります。そのような $y$ を求めると

$\displaystyle \frac{365}{\log(10000y)} < 1$

$\displaystyle \therefore 365 < \log(10000y) \fallingdotseq 9.2 + \log y$

$\displaystyle \therefore \log y > 355.8$

$\displaystyle \therefore y > e^{355.8} \fallingdotseq 10^{154}$

ということになります。

つまり、西暦が150桁ぐらいを超えない限り素数が0個になることはなさそうということですね。

宇宙誕生以来、まだ $10^{10}$ 年程度しか経っていないことを踏まえると、当分大丈夫そうです。

もちろん、上記の議論はあくまで確率的な議論です。素数かどうかは確率的に決まるのではなく、決定的なものですから、途中で突然素数が少ない年があってもおかしくはありません。

ちなみに西暦2000年からスタートして、西暦10000000まで、100000年置きにプロットしてみたのが次のグラフです。

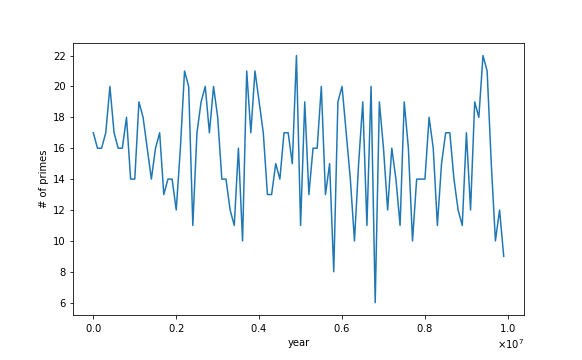
f:id:tsujimotter:20211225211232p:plain:w500

素数判定については、ミラー・ラビン法を用いたので、確率的素数の個数ということになります。（素数と判定されたものは、 $4^{-100}$ 未満の確率で合成数かもしれない）

もちろん飛び飛びでデータをとっていますので、この間で素数がなくなる年があっても不思議ではありませんが、減少傾向を見るにそこまで可能性は高くなさそうに見えます。

おわりに

そんなわけで、今回は「素数には毎年出会えるか？」をテーマに、yyyymmddの形で表される数が年間何個あるのかを考えてみました！

ヒューリスティックな議論ではありますが、素数が存在しない年は当分訪れないことが示されました。2021年は21個も素数の日があるそうです。

これで安心して素数ライフを送ることができますね！

次は 2022/01/03 にお会いしましょう！！

メリークリスマス！

みなさん良いお年を！！

2021.12.31追記：素数が存在しない最初の年が見つかりました！

なんと、素数が存在しない最初の年がしろねつさん（ @shironetsu ）により見つかりました！
最初の年は西暦13446204年とのことです！
shironetsu.hatenadiary.com

詳しくは記事を読んでいただきたいのですが、私の評価が $10^{154}$ 年程度だったのに対し、実際の最初の年ははるか昔だったというわけです。やはり、期待値の評価ではあまり当てにはならないということですね。

いやぁ、しかし面白い結果でした。自分で提起した問題が解決して、大変嬉しいです！

追い詰めるための手法も大変面白いので、ぜひしろねつさんの記事をご覧になってください。

tsujimotterのノートブック

日曜数学者 tsujimotter の「趣味で数学」実践ノート

カレンダーの上の素数〜素数には毎年出会えるか？〜

今日のテーマ

2022年は素数の日があります！

西暦3000年まではどうだろうか？

確率的に考えてみよう：素数定理

おわりに

2021.12.31追記：素数が存在しない最初の年が見つかりました！