ガウス和の性質についての証明 - tsujimotterのノートブック

前回の記事で、ガウス和 $G_p$ についての面白い定理を紹介しました。

せっかくなので、ガウス和シリーズと題して、３日連続でガウス和にまつわるお話を紹介したいと思います。このシリーズの全記事は「ガウス和」のタグで閲覧できるようにします。
tsujimotter.hatenablog.com

シリーズ第２回目の今回は、前回やり残した定理１の証明にチャレンジしたいと思います。

定理１

$\displaystyle G_p = \begin{cases} \sqrt{p} & p \equiv 1 \pmod{4} \\ \sqrt{-p} & p \equiv 3 \pmod{4} \end{cases}$

といいつつも、今回の記事では定理１のフルの証明を与えることができないことをあらかじめ断っておきます。

今回、実際に証明できるのは、次の定理２です。

定理２

$p\equiv 1 \pmod{4}$ のとき $p^* = p$ 、 $p\equiv 3 \pmod{4}$ のとき $p^* = -p$ とする。

このとき

$\displaystyle G_p^2 = p^*$

が成り立つ：

定理２は定理１と比べると少し弱い主張となっています。定理２からは、次の式が言えます。

$\displaystyle G_p = \pm\sqrt{p^*}$

ここで符号が $+$ であることがわかれば、定理１の主張そのものになりますので、定理２は符号決定の分だけ弱い主張になっているということですね。

ガウス和の符号を決定する問題を「符号決定問題」といいます。この問題は実に４年もの間、ガウスを悩ませた難問として知られています。この証明は大変複雑なので、ここでは扱いません。

問題を簡単化したとはいえ、定理２の証明もそれなりに難しく、いくつか段階を踏んで示す必要があります。それではいきましょう！

平方剰余の記号の性質

まず、平方剰余の記号（ルジャンドル記号といいます）についての性質を３つほど使います。（これらの定理の証明は省略します。）

命題３（平方剰余の準同型性）

$a, b$ を $p$ と互いに素な整数とする。

$\displaystyle \newcommand{qr}[2]{\left(\frac{#1}{\;#2\;}\right)}\qr{ab}{p} = \qr{a}{p}\qr{b}{p}$

命題４（平方剰余の第１補充則）

$\displaystyle \qr{-1}{p} = (-1)^{\frac{p-1}{2}}$

命題５

$\displaystyle \sum_{a = 1}^{p-1} \qr{a}{p} = 0$

命題５は、 $1 \leq a \leq p-1$ の範囲で「平方剰余と平方非剰余の個数は等しい」ことを主張する定理です。

１の原始p乗根に関する補題

次に、 $\zeta_p := \exp(2\pi i/p)$ という記号を導入します。これを使うと前回定義したガウス和をより簡潔に表せます。

$\displaystyle G_p = \sum_{k=1}^{p-1} \qr{k}{p} \zeta_p^k$

ここでは、今導入した $\zeta_p$ に関して、一つ補題を示したいと思います。証明自体はとても簡単です。

補題６

$\displaystyle \sum_{k = 1}^{p-1}\zeta_{p}^{kt} = \begin{cases} p-1 & (t \equiv 0 \pmod{p}) \\ -1 & (t \not\equiv 0 \pmod{p}) \end{cases}$

（補題６の証明）
$t \equiv 0 \pmod{p}$ のとき、 $\zeta_p^{kt} = 1$ となります。したがって、ただちに

$\begin{align} \displaystyle \sum_{k=1}^{p-1} \zeta_{p}^{kt} = p-1 \end{align}$

が得られます。

$t \not\equiv 0 \pmod{p}$ のとき、等比数列の和公式より

$\displaystyle \sum_{k=0}^{p-1} \zeta_{p}^{kt} = \frac{1-\zeta_{p}^{pt}}{1-\zeta_p^{t}}$

となります。ここで $\zeta_p^{pt} = 1$ より、右辺は 0 に一致します。

したがって

$\displaystyle \sum_{k=1}^{p-1} \zeta_{p}^{kt} = \sum_{k=0}^{p-1} \zeta_{p}^{kt} -1 = -1$

が得られます。

（補題６の証明終わり）

変数ずらしのテクニック

これにて証明のための補題が揃いました。

早速、定理２の証明にいきたいところなのですが、証明に向けて補足しておきたいテクニックが一つあります。これを証明に挟んでしまうと見通しが悪くなるので、あらかじめ紹介しておきたいと思います。私が勝手に「変数ずらしのテクニック」と呼んでいる方法です。

これから考えたいのは、整数を変数にとる関数 $g$ についての次のような和公式です。

$g$ を $\mathbb{Z}/p\mathbb{Z}$ から $\mathbb{C}$ への写像とする。ここで、 $k \in \mathbb{Z}/p\mathbb{Z}^\times$ に対して

$\displaystyle \sum_{a \in \mathbb{Z}/p\mathbb{Z}} g(a) = \sum_{a \in \mathbb{Z}/p\mathbb{Z}} g(ak)$

が成り立つ。

$g$ の変数を $a$ から $ak$ に置き換えたとしても、総和は一致するという主張です。

これを示すために、次の写像 $f$ を考えます：

$\begin{array}{rccl} f\colon &\mathbb{Z}/p\mathbb{Z} &\longrightarrow & \mathbb{Z}/p\mathbb{Z}, \\ & a & \longmapsto & ak \end{array}$

$p = 7, \; k = 2$ として例を考えてみましょう。

$(\mathbb{Z}/7\mathbb{Z})^\times$ の各元を「 $7$ 時間時計の文字盤の数字」だと思うことにすると、上の $f$ は文字盤の数をそれぞれ $2$ 倍する写像になっています。

f:id:tsujimotter:20200402213318p:plain:w400

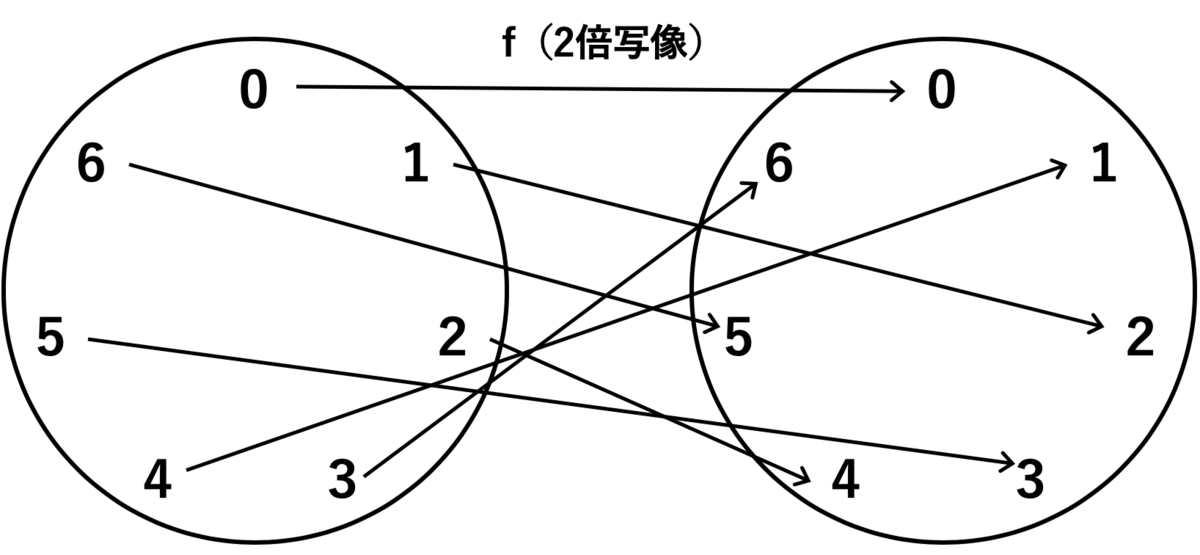
図の写像 $f$ は全単射になっていますね

一般の $p, k$ に対して、 $f$ が全単射であることを、次のように示します。

（単射性） $a, b \in \mathbb{Z}/p\mathbb{Z}$ に対して、 $f(a) = f(b)$ のとき $ak = bk$ です。任意の $k \in (\mathbb{Z}/p\mathbb{Z})^\times$ に対して逆元 $k^{-1}$ が存在することに注意して、両辺に $k^{-1}$ をかけると $a = b$ が得られます。よって $f$ は単射です。

（全射性）また、 $b \in \mathbb{Z}/p\mathbb{Z}$ に対して $f(a) = b$ なる $a$ は、 $a := k^{-1}b$ として得られます。よって $f$ は全射です。

以上から、 $f$ が全単射であることがわかりました。

よって、 $f\colon a \mapsto ak$ は全単射なので、次の和記号の等号が成立します：

$\displaystyle \sum_{a \in \mathbb{Z}/p\mathbb{Z}} g(a) = \sum_{a \in \mathbb{Z}/p\mathbb{Z}} g(ak)$

（以上のテクニックは、今後もよく使うので覚えておいてください。）

定理２の証明

それでは、定理２の証明に行きたいと思います。

$G_{p}^2$ を定義にしたがって計算します。

$\begin{array}{ll} G_{p}^2 &= \displaystyle \left(\sum_{k=1}^{p-1} \qr{k}{p}\zeta_{p}^{k} \right)\left(\sum_{a=1}^{p-1} \qr{a}{p}\zeta_{p}^{a} \right) \\ &= \displaystyle \sum_{k=1}^{p-1}\sum_{a=1}^{p-1} \qr{ka}{p}\zeta_{p}^{k+a} \end{array}$

ここで、上で説明した「変数ずらしのテクニック」を使います。

任意の $\overline{x} \in \mathbb{Z}/p\mathbb{Z}$ に対して $g$ を次の式で定めます。

$\displaystyle g(\overline{x}) := \begin{cases} \displaystyle \qr{kx}{p}\zeta_{p}^{k+x} & x\not\equiv 0 \pmod{p} \\ 0 & x\equiv 0\pmod{p} \end{cases}$

ここで、 $x$ は $\overline{x}$ の代表元を一つ選んだものとします。

これは $\overline{x}$ の代表元の取り方によらないことは、次のように示されます。

$g$ のwell-defined性：
$x, y \in \mathbb{Z}$ を $x \equiv y \pmod{p}$ であるようにとったとき

$\displaystyle \qr{kx}{p} = \qr{ky}{p}$

$\displaystyle \zeta_{p}^{k+x} = \zeta_{p}^{k+y}$

が成り立つ。したがって、 $g(\overline{x}) = g(\overline{y})$ となり、 $g$ は代表元の取り方によらないことが示された。

すると、 $g$ に $\overline{a}$ と $\overline{ak}$ をそれぞれ代入して得られる２つの和公式の間に、等号

$\displaystyle \sum_{\overline{a} \in \mathbb{Z}/p\mathbb{Z}} g(\overline{a}) = \sum_{\overline{a} \in \mathbb{Z}/p\mathbb{Z}} g(\overline{ak})$

が成立します。

添字の $\overline{a}$ について、 $1 \leq a \leq p-1$ の範囲で代表元をとって $g$ を計算すると

$\displaystyle \sum_{a=1}^{p-1} \qr{ka}{p}\zeta_{p}^{k+a} = \sum_{a=1}^{p-1} \qr{k(ak)}{p}\zeta_{p}^{k+ak}$

が成立します。

したがって、次のように式変形できます：

$\begin{array}{lll} G_{p}^2 &= \displaystyle \sum_{k=1}^{p-1}\sum_{a=1}^{p-1} \qr{ak^2}{p}\zeta_{p}^{k(a+1)} & \\ &= \displaystyle \sum_{k=1}^{p-1}\sum_{a=1}^{p-1} \qr{a}{p}\qr{k}{p}^2\zeta_{p}^{k(a+1)} & (\because \text{命題３より}) \\ &= \displaystyle \sum_{k=1}^{p-1}\sum_{a=1}^{p-1} \qr{a}{p}\zeta_{p}^{k(a+1)} & (\because \qr{k}{p}^2 = 1) \\ &= \displaystyle \sum_{a=1}^{p-1} \qr{a}{p} \sum_{k=1}^{p-1} \zeta_{p}^{k(a+1)} & \end{array}$

ここで、補題６に $t = a+1$ を代入することで

$\displaystyle \sum_{k = 1}^{p-1}\zeta_{p}^{k(a+1)} = \begin{cases} p - 1 & (a \equiv -1 \pmod{p}) \\ -1 & (a \not\equiv -1 \pmod{p}) \end{cases}$

が得られます。

したがって

$\begin{array}{lll} G_{p}^2 &= \displaystyle \sum_{a=1}^{p-2} \qr{a}{p} (-1) + \qr{-1}{p}(p-1) & \end{array}$

が得られます。

命題５より $\sum_{a=1}^{p-1} \qr{a}{p} = 0$ が成り立ちますが、和の中から $t = p-1$ の項だけ右辺に移項すると $\sum_{a=1}^{p-2} \qr{a}{p} = -\qr{-1}{p}$ となります。

これを上の式に代入すると次が得られます：

$\begin{array}{lll} G_{p}^2 &= \displaystyle \qr{-1}{p} + \qr{-1}{p}(p-1) & \\ &= \displaystyle \qr{-1}{p}p & \end{array}$

最後に、命題４（平方剰余の第１補充則）より、 $\qr{-1}{p} = (-1)^{\frac{p-1}{2}}$ ですが、この値は $p\equiv 1 \pmod{4}$ のとき $+1$ 、 $p\equiv 3 \pmod{4}$ のとき $-1$ の符号をとります。

以上により、定理２の主張が示されました。

（定理２の証明終わり）

おわりに

少し長かったですが「ガウス和の２乗が $p^*$ に一致する」を示すことができました。これを使えば、前回やったように面白い公式をいくらでも得ることができますね。

証明としては、 $f\colon \mathbb{Z}/p\mathbb{Z} \to \mathbb{Z}/p\mathbb{Z}, \; a \mapsto ak$ が全単射であることを使って、変数 $a$ を $ak$ へと「ずらすテクニック」がポイントでした。ガウス和は、こんな風に変数をずらしても計算できるように、うまく定義されていると感じます。