円分体の類体論の復習 - tsujimotterのノートブック

tsujimotter.hatenablog.com
以上の記事では，整数論にガロア理論を適用させ，素イデアルの分解法則を見出す「ヒルベルトの理論」の枠組みを紹介し，その系として円分体の分解法則を導きました。

上の記事から半年以上経っているので，円分体の類体論を復習しつつ，言い足りなかったことを少し補足したいと思います。

復習するテーマは大きく分けて以下の２つです。
・ガロア拡大における分解法則とフロベニウス
・円分体の素イデアル分解法則

この記事のすぐあとに，続きの記事を書きたいと思っています。今回の記事はそのための準備です。例によって，少々レベルが高い記事になりますが，よかったら合わせて読んでみてください。

復習１：ガロア拡大における分解法則とフロベニウス

まずは，問題設定とモチベーションを思い出しましょう。

$K\subset L$ を代数体のガロア拡大とします。ガロア拡大なので，ガロア群 $G = \mathrm{Gal}(L/K)$ を考えることができます。この設定の下で「 $K$ 上の素イデアル $\mathfrak{p}$ が拡大体 $L$ でどのように分解されるかを考えたい」というのがモチベーションであり，それを明らかにするのがヒルベルトの理論でした。

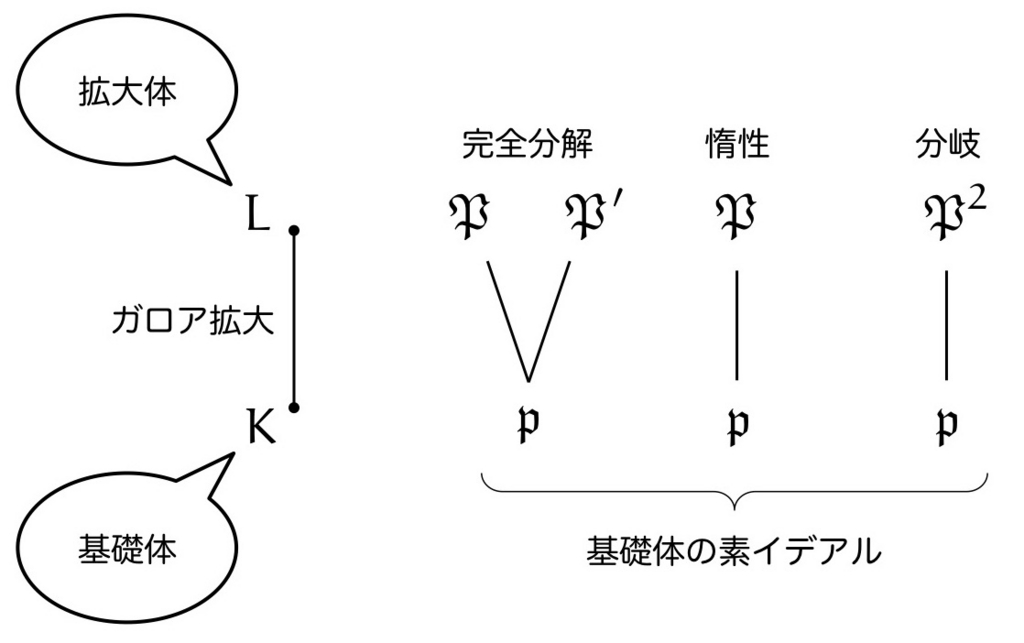
f:id:tsujimotter:20170101180121j:plain:w500

$L$ 上での $\mathfrak{p}$ の素イデアル分解を考え，素因子の１つを $\mathfrak{P}$ として固定しましょう（このとき $\mathfrak{p} \subset \mathfrak{P}$ が成り立ちますね）。

固定した $\mathfrak{P}$ に対して重要な $G$ の部分群，分解群 $Z_{\mathfrak{P}}$ と惰性群 $T_{\mathfrak{P}}$ を考えることができます。

一方で， $K$ の整数環 $\mathcal{O}_K$ を $\mathfrak{p}$ で割った有限体 $\mathcal{O}_K/\mathfrak{p}$ と $L$ の整数環 $\mathcal{O}_L$ を $\mathfrak{P}$ で割った有限体 $\mathcal{O}_L/\mathfrak{P}$ の間には， $(\mathcal{O}_L/\mathfrak{P})\big/ (\mathcal{O}_K/\mathfrak{p}$ ) という有限次拡大を考えることができました。この拡大のガロア群を $\tilde{G} = \mathrm{Gal}\left(\mathcal{O}_L/\mathfrak{P}\big/ \mathcal{O}_K/\mathfrak{p}\right)$ とします。

すると，次の図のような対応関係があって「代数体の拡大」と「有限体の拡大」が見事に結びつくのでしたね。

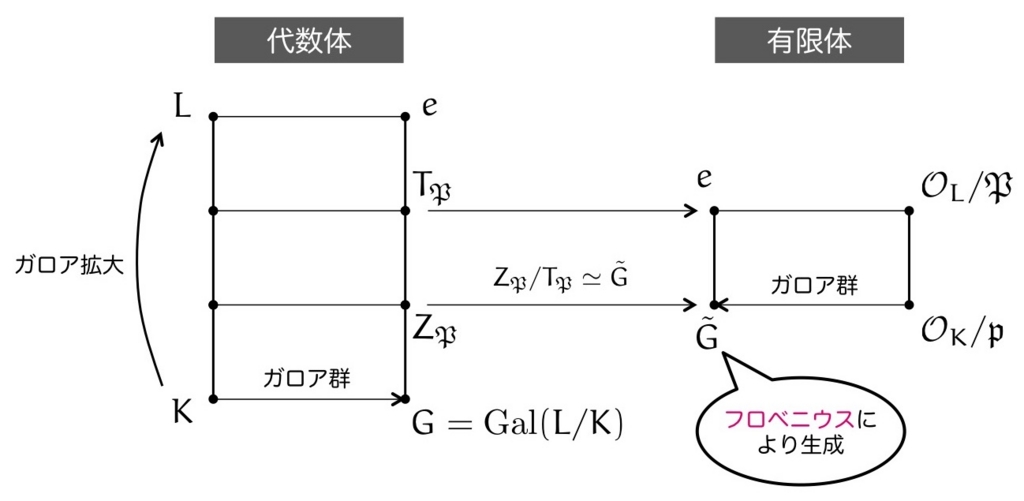
f:id:tsujimotter:20170101175517j:plain:w500

さらに都合の良いことに「有限体の拡大」のガロア群 $\tilde{G}$ はフロベニウス自己同型 $\alpha \mapsto \alpha^{N(\mathfrak{p})}$ によって生成されます。 $N$ はノルム写像で，定義は $\mathfrak{a}\subset \mathcal{O}_K$ に対して以下となります。

$N(\mathfrak{a}) := \#(\mathcal{O}_K/\mathfrak{a})$

したがって，拡大された有限体 $\mathcal{O}_L/\mathfrak{P}$ のうち，元の有限体 $\mathcal{O}_K/\mathfrak{p}$ に属していた元は「 $\mathcal{O}_K/\mathfrak{p}$ の個数乗」すると元に戻ってきて区別できるということです。これがフロベニウス自己同型の意味するところですね。

さらにこの拡大のガロア群は，このフロベニウス自己同型ただ１つによって生成される巡回群になっているというのです。有限体の世界はなかなか面白いです。

さて，有限個の素イデアルを除いて $\mathfrak{p}$ は不分岐です。不分岐であれば，惰性群 $T_{\mathfrak{P}}$ は潰れますから，分解群 $Z_{\mathfrak{P}}$ と $\tilde{G}$ は同型となります。

したがって， $\tilde{G}$ のフロベニウスに対応する代数体の自己同型が $Z_{\mathfrak{P}}$ に一対一で存在します。これを $L/K$ における $\mathfrak{P}$ のフロベニウス自己同型と呼びましょう*1。この元たった１つによって $Z_{\mathfrak{P}}$ が生成されるので「分解法則がよくわかる」というわけですね。

具体的には， $\mathfrak{p} \subset \mathfrak{P}$ を $L/K$ で不分岐とし $\mathfrak{P}$ のフロベニウス自己同型の位数を $f$ としたとき，この $f$ を使って $\mathfrak{p} \subset \mathfrak{P}$ の分解指数 $g$ は

$g = [L:K]\big/ f$

と表せることがわかります。

さて，代数体における $\mathfrak{P}$ のフロベニウス自己同型は，有限体 $\mathcal{O}_L/\mathfrak{P}$ に制限すると， $\alpha \mapsto \alpha^p$ という自己同型として振舞います。ここで $\alpha \in \mathcal{O}_L$ です。したがって，

$\sigma (\alpha)\equiv \alpha^{N(\mathfrak{p})} \pmod{\mathfrak{P}} \tag{1}$

を満たす $\sigma \in G$ が， $L/K$ における $\mathfrak{P}$ のフロベニウス自己同型です。この $\sigma$ を $\displaystyle \left[\frac{L/K}{\mathfrak{P}}\right]$ と書くことにしましょう。

※フロベニウス自己同型を定義する式 $(1)$ は頻繁に用いますので，ぜひ覚えておいてください。

補足１：フロベニウス自己同型とアーベル拡大

フロベニウス自己同型の定義において，今は $\mathfrak{P}$ を固定しています。この $\mathfrak{P}$ を入れ変えてしまった場合，フロベニウス自己同型は同じものになるのでしょうか。気になりますよね。

実は，単にガロア拡大であるだけでは，フロベニウス自己同型は $\mathfrak{P}$ の入れ替えによって異なるものに変わってしまいます。

まず， $\mathfrak{P}$ と共役な $\mathfrak{p}$ の素因数は，任意の $\tau \in G$ を用いて $\tau(\mathfrak{P})$ と表せることに注意します。 $\mathfrak{P}$ のフロベニウス自己同型を $\sigma$ としたとき，

$\sigma (\alpha)\equiv \alpha^{N(\mathfrak{p})} \pmod{\mathfrak{P}}$

が成り立ちますが，この式の両辺に $\tau$ を作用させましょう。

$\tau \circ \sigma (\alpha) \equiv \tau(\alpha)^{N(\mathfrak{p})} \pmod{\tau(\mathfrak{P})}$

さらに， $\alpha = \tau^{-1}(\beta)$ となるように $\beta \in \mathcal{O}_L/\mathfrak{P}$ をとると

$\tau \circ \sigma \circ \tau^{-1}(\beta) \equiv \beta^{N(\mathfrak{p})} \pmod{\tau(\mathfrak{P})}$

となります。すなわち， $\tau(\mathfrak{P})$ のフロベニウス自己同型は， $\tau \circ \sigma \circ \tau^{-1}$ となるわけです。記号を使って表すと，

$\displaystyle \tau \left[\frac{L/K}{\mathfrak{P}}\right] \tau^{-1} = \left[\frac{L/K}{\tau(\mathfrak{P})}\right]$

がいえるわけです。

ここまでは，一般のガロア拡大に対して考えてきました。もし， $G$ がアーベル群であれば，すなわち， $L/K$ がアーベル拡大であれば，上記の積は可換になります。したがって，

$\displaystyle \left[\frac{L/K}{\mathfrak{P}}\right] = \left[\frac{L/K}{\tau(\mathfrak{P})}\right]$

が言えます。標語的に言えば，フロベニウス自己同型は $\mathfrak{p}$ の素イデアル $\mathfrak{P}$ の取り方によらない，つまり， $\mathfrak{p}$ のみに依存するといえるわけです。そこで，アーベル拡大においては， $L/K$ における $\mathfrak{p}$ のフロベニウス自己同型を

$\displaystyle \left(\frac{L/K}{\mathfrak{p}}\right)$

と表すことにしましょう。この記号をアルティン記号と呼びます。

まとめると，アーベル拡大であればフロベニウスは基礎体 $K$ の素イデアル $\mathfrak{p}$ によって定まるという，非常に都合のよい性質を持ちます。一般のガロア拡大とアーベル拡大の違いが，このようなところに現れてくるのですね。

前回の記事はアルティン記号を用いないで進めました。それでもよいのですが，こうしておくと色々便利なことがあるので今回定義しました。まず，記号の $\mathfrak{p}$ が基礎体の素数となっているのがポイントですね。基礎体の情報だけで表せるというのが利点です。

補足２：アルティン写像と相互法則

後のために，アルティン記号をもう少しだけ拡張しておきましょう。

$K$ のイデアル $\mathfrak{a}$ は， $\mathfrak{a} = \mathfrak{p}_1^{e_1} \mathfrak{p}_2^{e_2} \cdots \mathfrak{p}_g^{e_g}$ のように一意に素因数分解できます。このとき， $L/K$ における $\mathfrak{a}$ のアルティン記号を

$\displaystyle \left(\frac{L/K}{\mathfrak{a}}\right) = \left(\frac{L/K}{\mathfrak{p}_1}\right)^{e_1} \left(\frac{L/K}{\mathfrak{p}_2}\right)^{e_2} \cdots \left(\frac{L/K}{\mathfrak{p}_g}\right)^{e_g}$

で定義します。すると，アルティン記号を $\mathfrak{a}$ に対しても定義できました。

注意して欲しいのは，この新しく拡張したアルティン記号は，もはや式 $(1)$ は満たさないということです。素イデアルではない $\mathfrak{a}$ に対するアルティン記号は「素イデアルに対するアルティン記号の形式的な積」以上の意味は持ちません。平方剰余のルジャンドル記号が素数 $p$ に対してしか意味をなさないのと同じです。今まで通り素イデアル $\mathfrak{p}$ に対しては，式 $(1)$ を満たします。

さて，こんなことをして何になるのでしょうか。実は，ちゃんと意味はあるのです。

まず， $K$ の任意のイデアル $\mathfrak{a}$ に対してアルティン記号を考えましょう。すると，すべての $\mathrm{Gal}(L/K)$ の元を尽くすことがわかります。

つまり， $K$ のイデアルを元として持つ群（これを便宜上「イデアル群」と呼びます）からガロア群への準同型写像が

$\displaystyle \mathfrak{a} \longmapsto \left(\frac{L/K}{\mathfrak{a}}\right)$

によって与えられ，全射になっているということです。この写像をアルティン写像と呼びます。アルティン写像は単射ではありませんが， $\displaystyle \left(\frac{L/K}{\mathfrak{a}}\right)$ が単位元（すなわち恒等写像）になる $\mathfrak{a}$ でつくられる部分群によって「イデアル群」を割ってあげれば全単射をつくれます。これがアルティン相互法則です。

「イデアル群」というものが何なのか定義をしないと本来は意味をなしませんが，難しいので今日はやめておきます。とにかく，この同型が具体的に与えられるという点が重要だということは覚えておいてください。

復習２：円分体の素イデアル分解法則

以下では， $K = \mathbb{Q}$ ， $L = \mathbb{Q}(\zeta_m)$ として，円分体の素イデアル分解法則を，具体的に考えていきましょう。

まず，円分体のフロベニウス自己同型を考えると， $\mathfrak{p} = (p)$ のフロベニウス自己同型は

$\displaystyle \left(\frac{\mathbb{Q}(\zeta_m)/\mathbb{Q}}{(p)}\right) \colon \zeta_m \mapsto \zeta_m^p \tag{2}$

となることがわかります。ちょっと大変ですが，今回はしっかり証明しましょう。ただし，一般の証明は難しいので， $m = l$ （素数）とします。

（証）
$p \neq l$ をそれぞれ素数とする。

$\alpha \in \mathcal{O}_{\mathbb{Q}(\zeta_l)} = \mathbb{Z}[\zeta_l]$ と $(p)$ の $\mathbb{Q}(\zeta_l)$ における分解の素因数 $\mathfrak{P}$ に対して， $p$ のフロベニウス写像を $\sigma_p$ とすると

$\sigma_p(\alpha) \equiv \alpha^p \pmod{\mathfrak{P}}$

が成り立つ。左辺は

$\begin{eqnarray} &&\sigma_p(a_0 + a_1\zeta_l + a_2 \zeta_l^2 + \cdots + a_{l-2} \zeta_l^{l-2}) \\ &&= a_0 + a_1\sigma_p(\zeta_l) + a_2 \sigma_p(\zeta_l)^2 + \cdots + a_{l-2} \sigma_p(\zeta_l)^{l-2} \end{eqnarray}$

であるから， $\sigma_p(\zeta_l)$ を調べればよい。 $\zeta_l \in \mathbb{Q}(\zeta_l)$ より

$\sigma_p(\zeta_l) = \zeta_l^p$

が成り立てば十分である。

一方， $\sigma_p \in \mathrm{Gal}(\mathbb{Q}(\zeta_l)/\mathbb{Q}) = \left\{ \zeta_l \mapsto \zeta_l^a \right\}$ より， $\sigma_p(\zeta_l) = \zeta_l^a$ となる $a$ （ただし， $1 \leq a \leq l-1$ ）が存在する。この $a$ を用いて

$\zeta_l^a \equiv \zeta_l^p \pmod{\mathfrak{P}}$

が得られる。（右辺）−（左辺）より

$\zeta_l^p(1-\zeta_l^{a-p}) \in \mathfrak{P}$

であるが， $\zeta_l^{p}$ は単数より

$1-\zeta_l^{a-p} \in \mathfrak{P} \tag{3}$

が成り立つ。

ここでもし $a \not\equiv p \pmod{l}$ ならば， $\zeta_l^{a-p}$ は１の原始 $l$ 乗根。
tsujimotter.hatenablog.com

上の記事で証明した補題により， $(l)$ は $\mathbb{Q}(\zeta_l)$ で完全分岐します。すなわち

$(l) = (1-\zeta_l)^{l-1}$

である。つまり， $l$ の $\mathbb{Q}(\zeta_l)$ 上の素因子は $(1-\zeta_l)$ に限られる。また $(1-\zeta_l) = (1-\zeta_l^k)$ である。 $p \neq l$ という条件，すなわち， $p$ と $l$ は素にもかかわらず， $p$ と $l$ が共通の素因子を持つことになる。これはおかしい。よって， $a \equiv p \pmod{l}$ である。

以上より， $\sigma_p(\zeta_l) = \zeta_l^p$ が得られた。

$p$ のフロベニウス自己同型 $\left(\frac{\mathbb{Q(\zeta_m)}/\mathbb{Q}}{(p)}\right)$ が式 $(2)$ により具体的にわかったので，この位数を調べることで $p$ の分解法則が完全にわかります。

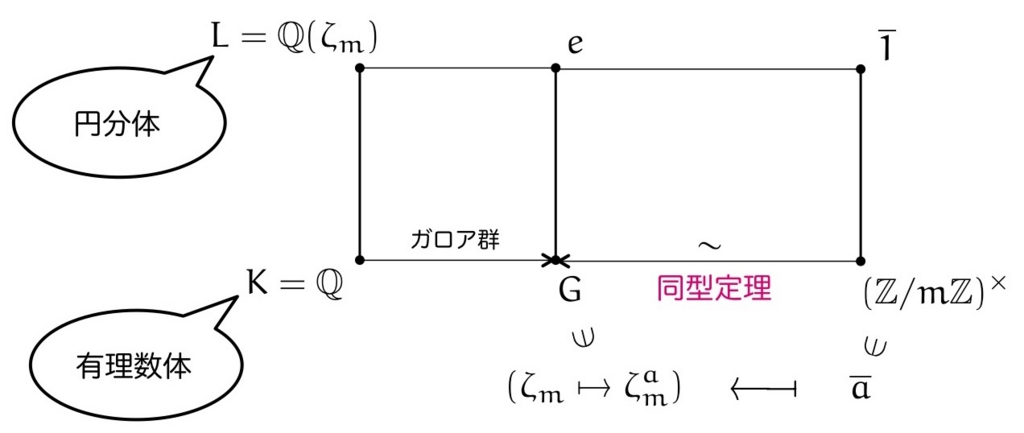
f:id:tsujimotter:20170101190726j:plain:w500

ここで，円分体のガロア群には以下のような同型があったことを思い出しましょう。

$(\mathbb{Z}/m\mathbb{Z})^\times \simeq \mathrm{Gal}(\mathbb{Q}(\zeta_m)/\mathbb{Q}) \tag{4}$

単に同型なだけでなく，以下のような対応によって具体的に与えられます（これが超重要です）。

$\displaystyle \overline{a} \longmapsto (\zeta_m \mapsto \zeta_m^a) \tag{5}$

$\overline{a}$ は， $a$ を代表元とする $(\mathbb{Z}/m\mathbb{Z})^\times$ の類を表します。つまり， $\overline{a} = a + m\mathbb{Z}$ ということです。

この同型写像により

$\displaystyle \overline{p} \longmapsto (\zeta_m \mapsto \zeta_m^p) = \left(\frac{\mathbb{Q(\zeta_m)}/\mathbb{Q}}{(p)}\right)$

と対応しますから， $p$ のフロベニウス自己同型 $\left(\frac{\mathbb{Q(\zeta_m)}/\mathbb{Q}}{(p)}\right)$ の位数は， $\overline{p}$ の $(\mathbb{Z}/m\mathbb{Z})^\times$ における位数に対応します。

したがって，以下の分解法則が得られます。

円分体の分解法則

$p$ を $\mathbb{Q}(\zeta_m)/\mathbb{Q}$ で不分岐な素数とし， $\overline{p}$ の $(\mathbb{Z}/m\mathbb{Z})^\times$ における位数を $f$ とすると， $p$ は $\mathbb{Q}(\zeta_m)/\mathbb{Q}$ において $\varphi(m)/f$ 個の素イデアルに分解する。

特に， $p \equiv 1 \pmod{m}$ であれば， $p$ は完全分解する。

以上で，円分体の分解法則が得られました。

最近よく使っている「 $p \equiv 1 \pmod{m}$ であれば， $p$ は完全分解する」という事実も，ちゃんと導くことができましたね。この法則の応用例はこちら。
tsujimotter.hatenablog.com

最後に，まだ触れていなかったアルティン相互法則について触れて終わりにしましょう。

式 $(5)$ をよーくみてみましょう。アルティン相互法則とほとんど同じ形をしていますね。

実際，アルティン相互法則

$\displaystyle \overline{a} \longmapsto \left(\frac{\mathbb{Q}(\zeta_m)/\mathbb{Q}}{(a)}\right)$

より式 $(5)$ を導くことができます。

$a = p_1^{e_1}p_2^{e_2}\cdots p_g^{e_g}$ と素因数分解しておくと，

$\displaystyle \overline{a} \longmapsto \left(\frac{\mathbb{Q}(\zeta_m)/\mathbb{Q}}{(p_1)}\right)^{e_1}\left(\frac{\mathbb{Q}(\zeta_m)/\mathbb{Q}}{(p_2)}\right)^{e_2}\cdots \left(\frac{\mathbb{Q}(\zeta_m)/\mathbb{Q}}{(p_g)}\right)^{e_g}$

のようにアルティン記号を分解できます。円分体のフロベニウスは式 $(2)$ より

$\displaystyle \left(\frac{\mathbb{Q}(\zeta_m)/\mathbb{Q}}{(p)}\right) = (\zeta_m \mapsto \zeta_m^p)$

で与えられますから，

$\displaystyle \overline{a} \longmapsto (\zeta_m \mapsto \zeta_m^{p_1})^{e_1}(\zeta_m \mapsto \zeta_m^{p_2})^{e_2}\cdots (\zeta_m \mapsto \zeta_m^{p_g})^{e_g}$