ナッシュの定理の証明：有限ゲームの混合戦略にはナッシュ均衡点が存在する

先日、予備校のノリで学ぶ「大学の数学・物理」さん（以下、ヨビノリさん）のYouTubeチャンネルにて、ゲーム理論に関する動画が公開されました。

www.youtube.com

ゲーム理論に関する基本的な用語について、大変わかりやすく紹介されているのでぜひご覧になってください。ゲーム理論において、重要な「解」概念である「ナッシュ均衡点」や「パレート効率」といった概念も紹介されていました。

さて、今回私の記事で紹介したいテーマは「ナッシュ均衡点の存在性」についてです。（混合戦略を考えない）純粋戦略のゲームにおいては、ナッシュ均衡点の存在しないゲームが存在します。具体的には、動画にも紹介された「じゃんけんゲーム」などがそうですね。

A＼B	グー	チョキ	パー
グー	$(0, 0)$	$(1, -1)$	$(-1, 1)$
チョキ	$(-1, 1)$	$(0, 0)$	$(1, -1)$
パー	$(1, -1)$	$(-1, 1)$	$(0, 0)$

一方で、（これもまた動画内で触れられていますが）混合戦略という、各プレーヤーが戦略を確率的に選ぶような状況にゲームを拡大すると、なんと必ずナッシュ均衡点が存在するということが知られています。

これは大変興味深い定理かと思います。

定理（ナッシュの定理）

有限個の戦略を持つ任意のゲームは、混合戦略の範囲でナッシュ均衡点を持つ。

もちろん、ナッシュ自身が「ナッシュ均衡点」と呼んだわけではありません。ナッシュがこの定理を示したからナッシュ均衡点という名前がついたわけですね。そして今やゲーム理論における超重要概念になっています。

tsujimotterは、三年ぐらい前からこの定理の証明をブログに書きたいと思っていました。しかしながら、ゲーム理論の基本的な設定を説明するのが面倒で、断念しておりました。ヨビノリさんの動画をみて、これはすばらしい、ぜひ乗っからせていただこう！と思ったのが執筆の経緯です。笑

ヨビノリさんの素晴らしい動画に感謝しつつ、証明を紹介させていただきます。

なお「ナッシュの定理」の証明には、不動点定理という定理が使われていまして、その定理の使いどころが今回の記事の一番のポイントになります。不動点定理自体の証明について今回はやりませんが、いったいどうやってナッシュ均衡点の存在を導くのかという点に着目して楽しんで頂ければと思います。

元々はヨビノリさんの動画からシームレスにつながるようなレベル感の記事にしようと思っていたのですが、どうもそれは難しそうです。内容が単純に難しいのです・・・。というわけで、それなりに数式も多くなってしまいますが、数学（特に集合と写像）にある程度慣れている人には読めるものにはなっているかと思います。

以前からゲーム理論を知っていた方でも、（ナッシュの定理の）証明は知らないという方も多いのではないでしょうか。有名な定理なので、一度はその証明に触れてみたいですよね。これを機にぜひ味わっていただきたいと思います。

最後まで通して読むのにはなかなか時間がかかると思いますので、読んでいる途中でも構いませんので

「（途中までしか読んでないけど）面白い！」とか
「ナッシュやばい！！」とか
「ベイマックスwww」とか

呟いていただけると嬉しいです。

それでは、じっくりお楽しみください！

目次：

1. ゲームの数学的定義

1-1. 標準形ゲーム

(a) プレーヤー集合

(b) 各プレーヤーの戦略集合

(c) 各プレーヤーの利得関数

(d) 具体例：囚人のジレンマ

1-2. 混合戦略ゲーム

(a) プレーヤー集合

(b) 各プレーヤーの戦略集合

(c) 各プレーヤーの利得関数

(d) 具体例：じゃんけんの混合戦略

1-3. その他、証明に必要な概念の導入

2. ブラウアーの不動点定理とその使いどころ

3. ナッシュの定理の証明

4. おわりに

参考文献（？）

1. ゲームの数学的定義

ヨビノリさんの動画は「数式なし」の解説をされていました。今回の記事は「証明の理解」が目的なので、数式を使ってゲーム理論を定式化していく必要があります。そのための準備をしたいと思います。

1-1. 標準形ゲーム

まず、標準形ゲームを定義したいと思います。一般にゲームは、プレーヤー集合・各プレーヤーの戦略集合・各プレーヤーの利得関数の３点により定義されます。

(a) プレーヤー集合

$n$ 人のプレーヤーの集合を

$N = \{1, 2, \ldots, n\}$

とします。任意のプレーヤーを取り出して表すときは、この集合の要素として $i \in N$ と表します。

プレーヤーに対する添え字としては、本記事を通して記号 $i$ を用いることにします。時折、 $i$ が $N$ の要素であることを明記し忘れるかと思いますが、その場合は察してください。

(b) 各プレーヤーの戦略集合

プレーヤー $i \in N$ の戦略集合を

$S_i = \{1, 2, \ldots, m_i\}$

とします。じゃんけんゲームであれば、グーが $1$ 、チョキが $2$ 、パーが $3$ みたいな感じですね。プレーヤー一人一人の戦略が異なる状況も想定されるので、戦略集合はプレーヤーごとに設定します。

プレーヤーのときと同じように、戦略の添え字記号としては $j \in S_i$ あるいは $j_i \in S_i$ などを用いることにします。

したがって、プレーヤー全体の戦略の組み合わせは、直積集合

$S := S_1 \times S_2 \times \cdots \times S_n$

で表せることになりますね。

(c) 各プレーヤーの利得関数

任意の戦略の組み合わせ $(j_1, \ldots, j_n) \in S$ に対して、プレーヤー $i \in N$ の利得が決まります。よって、実数値関数

$u_i \colon \;\; S \longrightarrow \mathbb{R}$

を、プレーヤー $i$ の利得関数としましょう。各プレーヤーの戦略の組 $(j_1, \ldots, j_n) \in S$ が与えられると、プレーヤー $i$ の利得 $u_i(j_1, \ldots, j_n)$ という実数値が定まります。

これで有限個の戦略を持つ標準形ゲームが定義されました。

(d) 具体例：囚人のジレンマ

ヨビノリさんの動画の「囚人のジレンマ」の例を利用しましょう。プレーヤー集合を

$N = \{1, 2\}$

として、各プレーヤーの戦略集合はどちらも共通の集合

$S_1 = S_2 = \{1, 2\}$

をとります。（ $1$ が「黙秘」、 $2$ が「自白」という対応関係ですね。）

また、囚人のジレンマにおける利得関数の定義は次のようになります。

$u_1(1, 1) = -2,\; u_2(1, 1) = -2$	$u_1(1, 2) = -10 ,\; u_2(1, 2) = 0$
$u_1(2, 1) = 0,\;\;\; u_2(2, 1) = -10$	$u_1(2, 2) = -5,\;\;\, u_2(2, 2) = -5$

これは下記の利得表に対応していますので、確認してみてください。

A＼B	「黙秘」	「自白」
「黙秘」	$(-2, -2)$	$(-10, 0)$
「自白」	$(0, -10)$	$(-5, -5)$

1-2. 混合戦略ゲーム

ここからは混合戦略を定義したいと思います。

混合戦略のイメージとしては、標準形ゲームの各戦略を確率的に選ぶような感じです。簡単のために、プレーヤー $1$ が1人でプレーする「相手のいないゲーム」を考えてみましょう。利得としては

$u_1(1) = 10, \;\; u_1(2) = -3$

とします。つまり、戦略 $1$ を選ぶと利得が $10$ であり、戦略 $2$ を選ぶと利得が $-3$ になる状況を考えるわけですね。右に行ったらゴール、左に行ったら落とし穴みたいなゲームですかね。（何が面白いんだろう、このゲーム。）

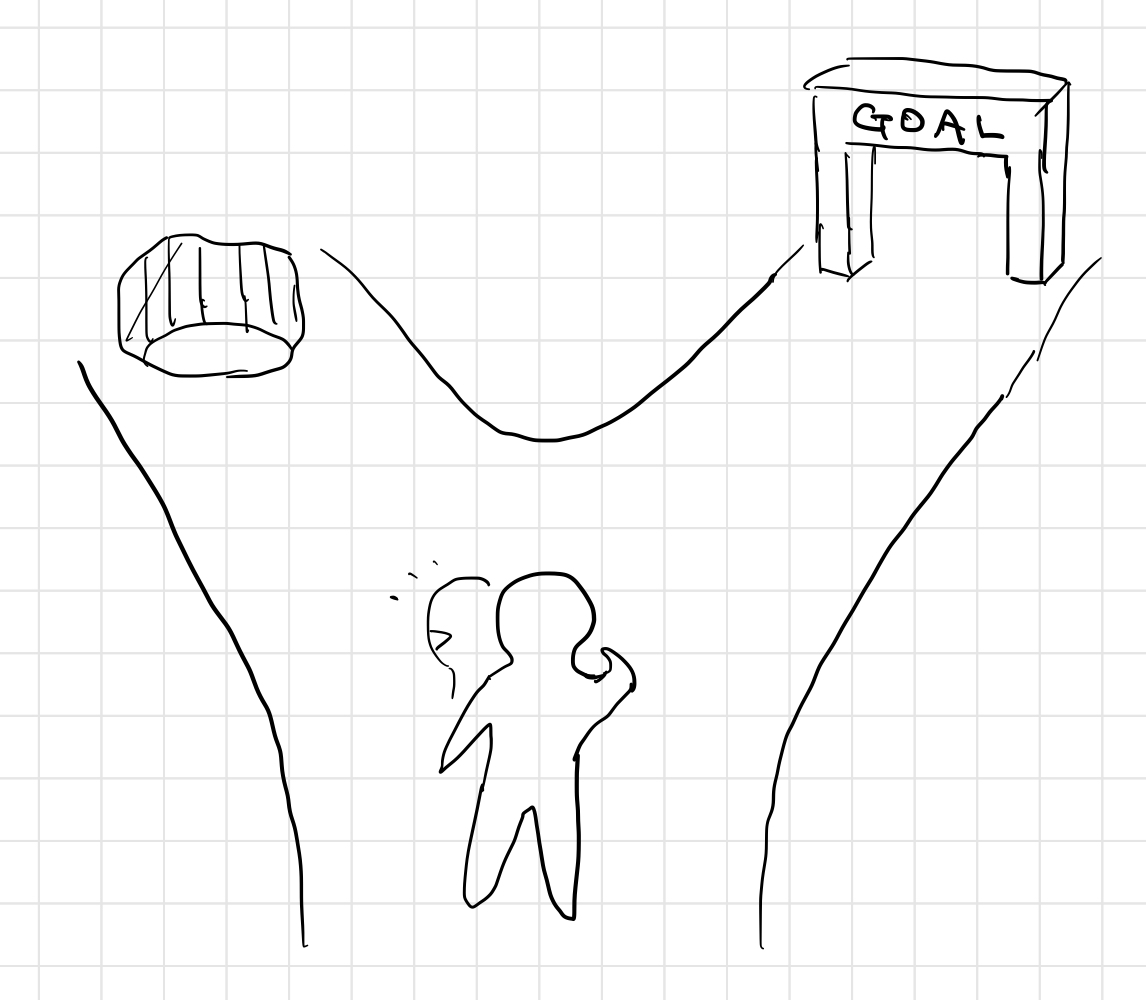
f:id:tsujimotter:20210219170840j:plain:w260

ここでプレーヤー $1$ が、右にいく確率を $0 \leq x_1 \leq 1$ として、左にいく確率を $0\leq x_2 \leq 1$ とします。この確率のペア $(x_1, x_2)$ 自体を戦略だと思うことにしましょう。これを混合戦略と言います。プレーヤーの選択は確率に従うので、それぞれの戦略を選択する確率の和は $x_1 + x_2 = 1$ となることに注意しましょう。

すると、プレーヤー $1$ が混合戦略 $(x_1, x_2)$ をとったとき、得られる利得（の期待値）は

$x_1 u_1(1) + x_2 u_1(2)\;\; =\;\; 10x_1 - 3(1-x_1) \;\; = \;\; 13x_1 - 3$

となりますね。これが混合戦略における利得関数というわけです。

一方で、「確率 $1$ で戦略 $1$ を選ぶ（確率 $0$ で戦略 $2$ を選ぶ）」のようなものも、立派な混合戦略です。この場合 $(x_1, x_2) = (1, 0)$ のように表現します。特に、このような混合戦略のことを純粋戦略といいます。

それでは、標準形ゲームの混合戦略への拡大を以下で定義します。

(a) プレーヤー集合

まず、プレーヤーの集合は変わらず

$N = \{1, 2, \ldots, n\}$

です。

(b) 各プレーヤーの戦略集合

次に、プレーヤー $i \in N$ の混合戦略に拡大した戦略集合 $X_i$ ですが、プレーヤー $i$ が戦略 $1$ を選ぶ確率を $x_{i1} \geq 0$ 、戦略 $2$ を選ぶ確率を $x_{i2} \geq 0$ 、・・・のように定義していきます。最終的に、戦略それぞれに対しての選択確率の和は

$\displaystyle \sum_{j\in S_i} x_{ij} = x_{i1} + \cdots + x_{im_i} = 1$

となることに注意しましょう。したがって、プレーヤー $i \in N$ の混合戦略の集合は

$X_i := \{ (x_{i1}, \ldots, x_{i m_i}) \in \mathbb{R}^{m_i} \mid \; x_{i1} \geq 0, \;\ldots, \; x_{im_i} \geq 0, \; \sum_{j \in S_i} x_{ij} = 1 \}$

となります。だいぶややこしい集合ですが、意味するところは上で説明した通りです。

ちなみに、この集合 $X_i$ は数学的には「単体（simplex）」と呼ばれる集合になっています。 $m_i$ 次元空間における「三角形」を表す図形なのですが、具体的に図示してみるとイメージしやすいかもしれません：

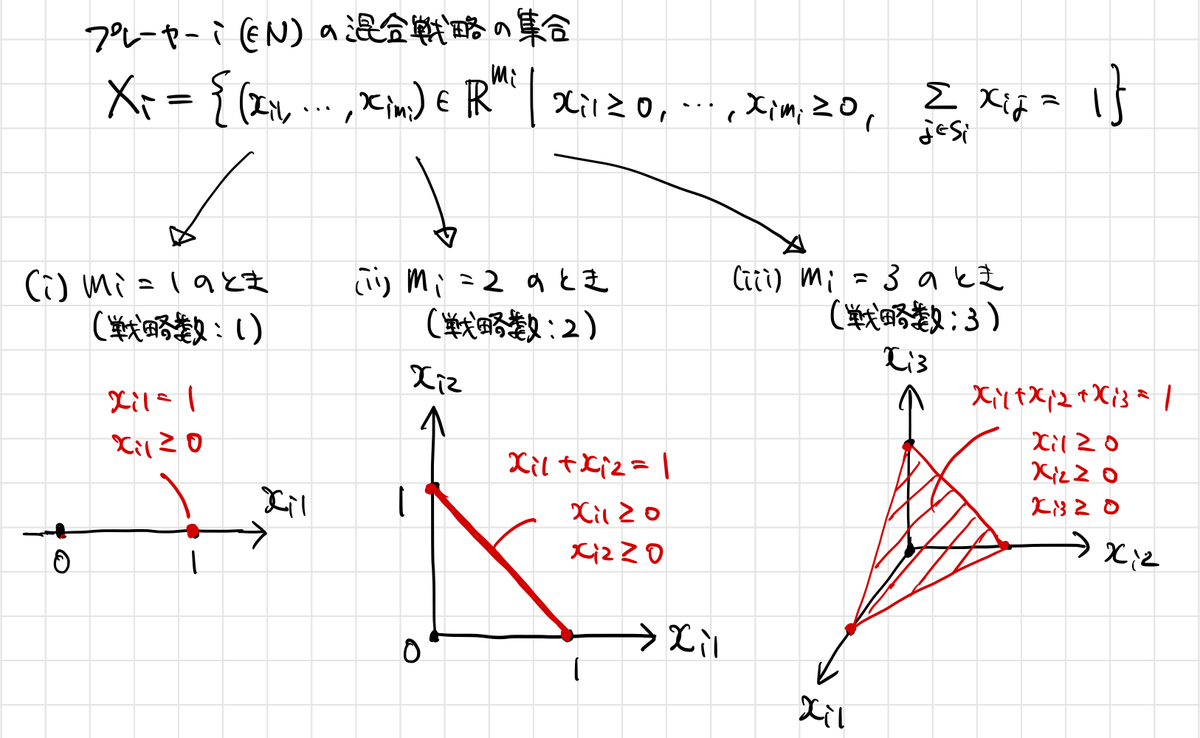
f:id:tsujimotter:20210219212254j:plain:w560

$m_i = 1$ （戦略数: $1$ ）のときは「点」（図左）、
$m_i = 2$ （戦略数: $2$ ）のときは「線分」（図中央）、
$m_i = 3$ （戦略数: $3$ ）のときは「三角形」（図右）

よって、プレーヤー全体の混合戦略の組み合わせは、 $X_i$ の直積となりますので

$\displaystyle X := X_1 \times \cdots \times X_n$

ということですね。

(c) 各プレーヤーの利得関数

プレーヤー $i$ の利得関数は、関数 $v_i\colon \; X \longrightarrow \mathbb{R}$ だと思うことができます。 $v_i$ は、次で定義されます：

$\displaystyle v_i(x_1, \ldots, x_n) = \sum_{(j_1, \ldots, j_n) \in S} \underline{x_{1 j_1} \cdots x_{n j_n}}\; u_i(j_1, \ldots, j_n)$

添え字が多くてややこしいですね。要するに、下線部が（純粋）戦略 $(j_1, \ldots, j_n) \in S$ が選択される確率を表していて、このときの期待利得が計算されているというわけです。総和記号は $(j_1, \ldots, j_n) \in S$ のすべての組に対する和をとっています。

(d) 具体例：じゃんけんの混合戦略

しばらく抽象的な議論が続いたので具体例を挟みます。じゃんけんゲームの時には、プレーヤー $i = 1, 2$ の取れる混合戦略は

$x_{i1}$ ：「グー」を選択する確率
$x_{i2}$ ：「チョキ」を選択する確率
$x_{i3}$ ：「パー」を選択する確率

の組 $(x_{i1}, x_{i2}, x_{i3})$ となります。ここで、プレーヤー $i = 1, 2$ の混合戦略をどちらも

$(x_{i1}, x_{i2}, x_{i3}) = (1/3, 1/3, 1/3)$

としてみましょう。これは、グー・チョキ・パーをそれぞれ確率 $1/3$ で出すということです。完全にランダムに出すということですね。

f:id:tsujimotter:20210219214010j:plain:w280

実は、上記の「確率 $1/3$ の混合戦略」をお互いに選択する解が、じゃんけんの混合戦略におけるナッシュ均衡点となっています。証明はしないですが、なんとなく直感的に正しそうですよね。そりゃ均等に出した方が良さそうです。

これによって標準形ゲームのときにはナッシュ均衡が存在しなかったじゃんけんゲームですが、混合戦略に拡大したことによってナッシュ均衡が現れたわけです。これが一般の有限ゲームについてに成り立つというのが、ナッシュの定理の主張ですね。

これは余談ですが、人間が完全にランダムで手を出すのは難しいみたいですね。だいたいみんな何かしらの出す手の傾向があって、それにしたがって手を出しているそうです。この傾向を機械に学習させてしまうと、人間が勝てなくなるみたいな実験があったのを聞いた覚えがあります。

1-3. その他、証明に必要な概念の導入

さて、これにて基本的な設定が定義できました。証明のためにはもうちょっとだけ道具が必要になりますので、もうしばらくお付き合いください。

まず、混合戦略の組を表す便利な表現を導入します。プレーヤー $i$ の戦略を $x_i \in X_i$ としたとき

$\mathbf{x} = (x_1, \ldots, x_n) \in X$

がすべてのプレーヤーの混合戦略の組を表します。ベクトルのようなものだと思ってくれていいのですが、1プレーヤーの混合戦略 $x_i$ 自体は「各戦略を選択する確率の組」になっていることに注意しましょう。

また、特定のプレーヤー $i$ に着目したときに、 $\mathbf{x}$ の要素を $x_i$ とそれ以外に分けて

$\mathbf{x} = (x_{-i}, \; x_{i})$

と表現することがあります。 $x_{-i}$ は $i$ 番目の要素以外のすべて要素の組だと思ってください。こうしておくと、 $i$ 番目のプレーヤーだけ混合戦略を置き換える、みたいなことができるわけですね。これは大変便利な表現なので多用します。

これを使うと、ナッシュ均衡点の定義が簡便に表現できます。

定義（ナッシュ均衡点）

混合戦略の組 $\mathbf{x}^* \in X$ がナッシュ均衡点であるとは、任意の $i \in N$ および $y_i \in X_i$ に対して

$v_{i}(\mathbf{x}^*) \geq v_{i}(x_{-i}^*, \; y_i)$

を満たすことをいう。

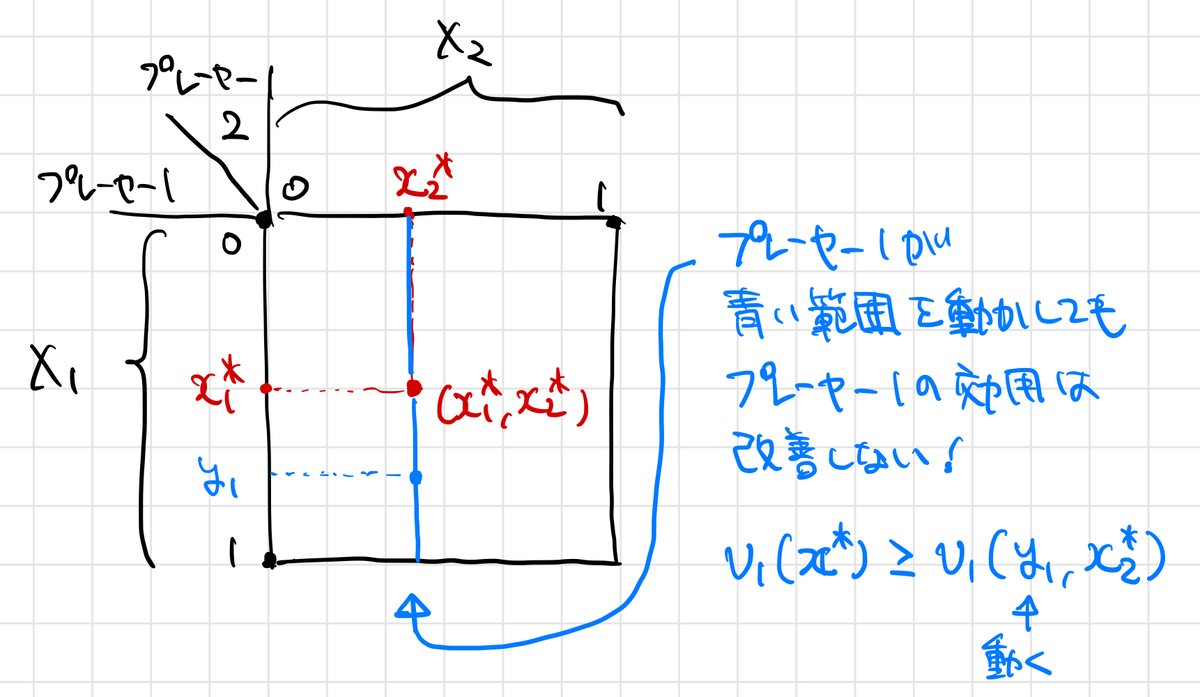
つまり、他のプレーヤーの混合戦略を $x_{-i}^*$ に固定しつつ、プレーヤー $i$ の混合戦略だけを動かしたとき、プレーヤー $i$ にとっては $x_i^*$ が最適応答戦略になっている。これが全プレーヤーに対して成り立つ状況がナッシュ均衡点というわけですね。

f:id:tsujimotter:20210219212917j:plain:w420

次に、 $X$ 上で定義される関数 $g_{ij}$ を次のように定義しましょう。 $\mathbf{x} \in X, \;\; i \in N, \;\; j \in S_i$ に対して

$g_{ij}(\mathbf{x}) = \max\left\{ 0, \;\; v_i(x_{-i}, \; e_{ij}) - v_i(\mathbf{x}) \right\}$

と定義します。ここで、 $e_{ij} = (0, \ldots, 0, \overset{j}{1}, 0, \ldots, 0)$ とします。これは $j$ 番目だけ $1$ 、それ以外は $0$ であるような組です。意味としては「確率 $1$ で戦略 $j$ を選択する」というプレーヤー $i$ の純粋戦略を表現するものだと思ってください。

$v_i(x_{-i}, e_{ij}) - v_i(\mathbf{x})$ の部分だけ取り出すと

$v_i(\mathbf{x})$ は混合戦略の組 $\mathbf{x}$ におけるプレーヤー $i$ が受け取る期待利得
$v_i(x_{-i}, \; e_{ij})$ は混合戦略の組 $\mathbf{x}$ に対して、プレーヤー $i$ だけ戦略 $j$ の純粋戦略に置き換えたときに、プレーヤー $i$ が受け取る期待利得

を表します。この差をとっていますので、（他のプレーヤーの戦略そのままに）プレーヤー $i$ だけ戦略 $j$ の純粋戦略に置き換えたときの期待利得の差を表しているわけです。

これと $0$ のmaxをとっているので、これが正であれば $g_{ij}(\mathbf{x})$ に値が現れるわけですね。それ以外のときは $0$ の値をとる関数です。

2. ブラウアーの不動点定理とその使いどころ

さて、定理の証明の一つのキーポイントとして、不動点定理を紹介します。

一口に不動点定理といっても、実は色々なバリエーションがあります：

ブラウアーの不動点定理
角谷の不動点定理（ブラウアーの不動点定理の一般化）

ナッシュ均衡の証明にも色々なバリエーションがあり、それぞれ使用する不動点定理が異なります。

ナッシュ自身は、最初は「角谷の不動点定理」を用いた証明を発表したようです。その後、証明を改良して、博士論文やThe Annals of Mathematicsに掲載された論文においては、「ブラウアーの不動点定理」を直接使った証明を紹介しています。今回はこちらの方法を紹介したいと思います。

定理（ブラウアーの不動点定理）

$C$ をユークリッド空間内のコンパクト凸集合とします。 $f$ を $C$ から $C$ の中への連続写像とします。このとき、 $f$ は不動点を持つ。

つまり、 $f(x^*) = x^*$ なる $x^* \in C$ が存在する。

この定理の意味するところは比較的わかりやすいかと思います。つまり、空間内の条件を満たす集合があったときに、それを縮小するような写像を考えると、その縮小によって動かない点が存在するということです。

たとえば、平面内の凸集合の例として「ベイマックス」を考えます。

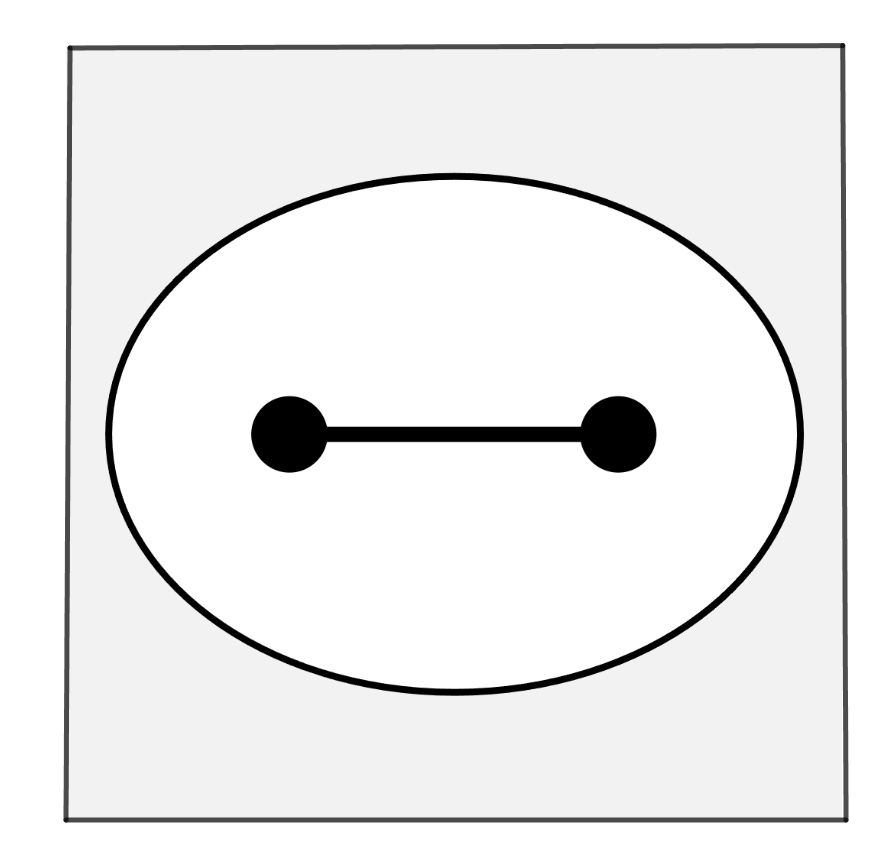
f:id:tsujimotter:20210218224835p:plain:w280

この集合を縮小する写像 $f$ を考えると、次のようになります。

pic.twitter.com/dDAsYiQWPe
— tsujimotter ロマ数本好評発売中!! (@tsujimotter) 2021年2月18日

よーく観察すると、少なくとも1点、移動前と移動後で動いていない点が現れます。そういう定理です。

不動点定理を適用するために、混合戦略の集合 $X$ が「コンパクト凸集合」の条件を満たすか確認してみましょう。

まず、プレーヤー $i \in N$ の混合戦略の集合 $X_i$ は、先ほど述べたように単体集合ですが、特にコンパクト集合でもあります。さらに凸集合です。

「コンパクト」は位相空間論の用語ですが、ユークリッド空間においては、

コンパクト　 $\Longleftrightarrow$ 　有界閉集合

なので、コンパクトがよくわからない人は「有界」かつ「閉集合」という理解でいいと思います。

また、コンパクト凸集合の直積もまたコンパクト凸集合です。したがって

$X = X_1 \times \cdots \times X_n$

もコンパクト凸集合です。これで $X$ が定理の条件を満たすことがわかりました。

よって、 $X$ から $X$ への連続写像 $f$ を考えて、 $f$ の不動点がちょうどナッシュ均衡になるようにできれば良さそうですね。これが証明の基本的な方針です。

問題は、その方針を実行するためにどんな $f$ をとったらよいかということです。ここが一番頭を使うポイントです。

結論から言うと、次のような関数 $f\colon X \longrightarrow X$ を考えます。

まず、準備として $f_{ij}\colon X \to [0, 1]$ を次のように用意します：

$\displaystyle f_{ij}(\mathbf{x}) = \frac{x_{ij} + g_{ij}(\mathbf{x})}{1 + \sum_{j \in S_i} g_{ij}(\mathbf{x})}$

ここで、プレーヤー全体の混合戦略の組を $\mathbf{x} = (x_1, \ldots, x_n) \in X$ として、各プレーヤー $i$ が各戦略を選択する確率を $x_i = (x_{i1}, \ldots, x_{im_i})$ としています。 $x_{ij}$ はプレーヤー $i$ が戦略 $j$ を選ぶ確率です。

なんじゃこりゃというような関数ですが、これを並べたものが目的の $f$ です。

すなわち、任意の $i\in N$ に対して

$f_i(\mathbf{x}) := ( f_{i1}(\mathbf{x}), \ldots, f_{im_i}(\mathbf{x}) )$

として、さらに

$f(\mathbf{x}) := ( f_{1}(\mathbf{x}), \ldots, f_{n}(\mathbf{x}) )$

のように定義します。これによって、 $f\colon X \longrightarrow X$ が得られます。

実際、 $f_i(\mathbf{x}) \in X_i$ が成り立つこと（つまり、 $f_i(\mathbf{x})$ の要素をすべて足して $1$ になること）は確認する必要がありますが、次の通り示せます：

$\displaystyle \sum_{j \in S_i} f_{ij}(\mathbf{x}) = \frac{\sum_{j \in S_i} x_{ij} + \sum_{j \in S_i} g_{ij}(\mathbf{x})}{1 + \sum_{j \in S_i} g_{ij}(\mathbf{x})} = 1$

途中で $\sum_{j \in S_i} x_{ij} = 1$ を使っています。

よって、任意の $i \in N$ で $f_i(\mathbf{x}) \in X_i$ が成り立つこと、すなわち $f(\mathbf{x}) \in X$ であることが示されました。

また、 $g_{ij}(\mathbf{x})$ は（よーく考えると）連続関数であることがわかり、 $f_{ij}$ はその四則演算で得られるので連続関数。よって、 $f$ のすべての要素は連続なので、直積位相の性質により $f$ は連続写像です。

ゆえに、ブラウアーの不動点定理により、 $f$ は不動点を持つことになります。つまり、 $f(\mathbf{x}^*) = \mathbf{x}^*$ なる $\mathbf{x}^* \in X$ が存在することになります。

3. ナッシュの定理の証明

不動点定理を使って、謎の関数 $f\colon X \longrightarrow X$ は不動点 $\mathbf{x}^*$ を持つことがわかりました。

実はこの $\mathbf{x}^*$ がナッシュ均衡点であった、というのが得たい結論です。これを示すことができれば証明が完結します。

不動点 $\mathbf{x}^*$ について、 $f(\mathbf{x}^*) = \mathbf{x}^*$ が成り立つわけですから、 $f$ の定義より

$\displaystyle x_{ij}^* = \frac{x_{ij}^* + g_{ij}(\mathbf{x}^*)}{1 + \sum_{j\in S_i} g_{ij}(\mathbf{x}^*)}$

が成り立ちます。すなわち

$\displaystyle x_{ij}^* \sum_{j\in S_i} g_{ij}(\mathbf{x}^*) = g_{ij}(\mathbf{x}^*) \tag{*}$

が成立します。

ここで、次の補題を証明します：

補題

$\mathbf{x} \in X$ とする。任意の $i \in N$ に対して、ある $j \in S_i$ が存在して

$x_{ij} > 0 \;\; \text{かつ} \;\; g_{ij}(\mathbf{x}) = 0 \tag{**}$

が成り立つ。

（補題の証明）
$v_i$ の定義より

$\displaystyle v_i(\mathbf{x}) = \sum_{j\in m_i} x_{ij} v_i(x_{-i}, \, e_{ij}) = \sum_{j \in S_i, \; x_{ij} > 0} x_{ij} v_i(x_i, \, e_{ij}) \tag{***}$

が成り立つ。（プレーヤー $i$ だけ純粋戦略に分解した。）

さて、補題の主張が誤りだと仮定する。このとき

ある $i \in N$ が存在して、任意の $j \in S_i$ に対して、 $x_{ij} > 0$ ならば $g_{ij}(\mathbf{x}) > 0$

が成り立つ。この $i$ を固定すると、関数 $g_{ij}$ の定義より

任意の $j$ に対して $g_{ij}(\mathbf{x}) > 0$ ならば $v_{i}(x_{-i}, \, e_{ij}) > v_{i}(\mathbf{x})$

が成り立つ。 $\sum_{j \in S_i} x_{ij} = 1$ より

$\displaystyle \begin{align} \sum_{j \in S_i, \; x_{ij} > 0} x_{ij} v_{i}(x_{-i}, \, e_{ij}) &> \sum_{j \in S_i, \; x_{ij} > 0} x_{ij} v_{i}(\mathbf{x}) \\ &= v_i(\mathbf{x}) \sum_{j \in S_i, \; x_{ij} > 0} x_{ij} \\ &= v_i(\mathbf{x}) \end{align}$

が成り立つ。しかし、 $(\ast\ast\ast)$ と合わせると $v_i(\mathbf{x}) > v_i(\mathbf{x})$ が成り立ってしまうがこれはおかしい。

ゆえに「補題の主張が誤り」という仮定が誤りであった。

（補題の証明終わり）

補題の式 $(**)$ に $\mathbf{x} = \mathbf{x}^*$ （ $f$ の不動点）を代入すると、任意の $i \in N$ に対してある $j \in S_i$ が存在して

$x_{ij}^* > 0$ かつ $g_{ij}(\mathbf{x}^*) = 0$

が成り立つことがわかります。ところが、式 $(*)$ を思い出すと

$\displaystyle x_{ij}^* \sum_{j\in S_i} g_{ij}(\mathbf{x}^*) = g_{ij}(\mathbf{x}^*)$

であったから、右辺が $0$ になります。左辺に着目すると、 $x_{ij}^* > 0$ より

$\displaystyle \sum_{j\in S_i} g_{ij}(\mathbf{x}^*) = 0$

であることがわかります。

$g_{ij}(\mathbf{x})$ は定義より $0$ 以上なので、これはつまり

任意の $i \in N$ 、 $j \in S_i$ に対して $g_{ij}(\mathbf{x}^*) = 0$

であることを意味します。

2021.03.05訂正：上の式で「任意の $i \in N$ 、 $j \in S_i$ に対して $g_{ij}(\mathbf{x}^*) \geq 0$ 」と書いていましたが、正しくは「任意の $i \in N$ 、 $j \in S_i$ に対して $g_{ij}(\mathbf{x}^*) = 0$ 」でした。既に訂正させていただいています。

言い換えると

任意の $i \in N$ 、 $j \in S_i$ に対して $v_{i}(x_{-i}^*, \, e_{ij}) \leq v_{i}(\mathbf{x}^*)$

ということです。（プレーヤー $i$ の混合戦略をいずれかの純粋戦略 $e_{ij}$ に置き換えたとき、プレーヤー $i$ の利得は元の利得以下となる。）

これを用いると、任意の混合戦略 $y_i \in X_i$ に対して

$\displaystyle \begin{align} v_{i} \, (x_{-i}^*, \, y_i) &= \sum_{j \in S_i} y_{ij} \, v_i(x_{-i}^*, \, e_{ij}) \\ &\leq \sum_{j \in S_i} y_{ij}\, v_i(\mathbf{x}^*) \end{align}$