tsujimotter.hatenablog.com
上の記事では、穴あき円板 上のド・ラームコホモロジー
を計算しました。
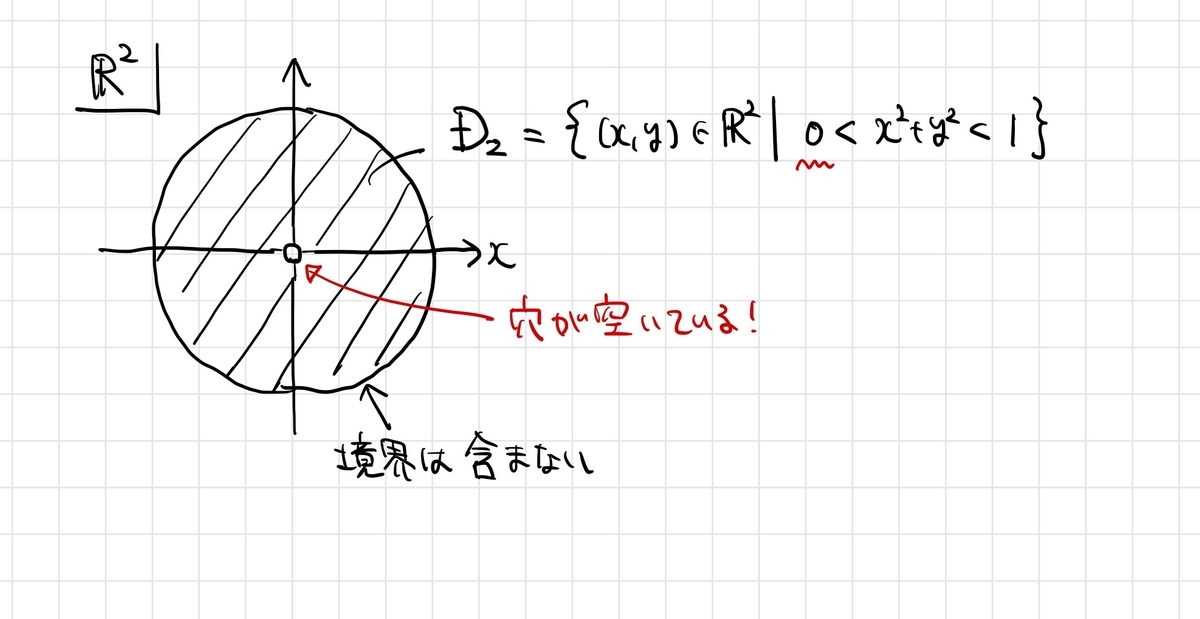
ド・ラームコホモロジーを計算するには、 上の任意の閉1形式(
の元)を計算し、それと完全1形式(
の元)との「差」(実際は商ベクトル空間)を計算する必要があります。
このとき、非自明な元
が存在して、 が閉1形式でありながら完全1形式ではないことを示しました。
前回の記事では、「ド・ラームの定理」という非常に大きな定理を使うことで、 の
上の次元が1であることを示し、結果として
が1次元の基底をなすことを示したのでした。
しかしながら、ド・ラームの定理を使うのはちょっと大掛かりすぎますね。もっと直接的に示す方法はないものかと思っていました。そんな折に、ラスクさん( @washoi4150 )という方からTwitterで「直接的に示す方法はあるよ」と教えていただけました。
そこで今回は、ラスクさんに許可をいただきまして、 上のド・ラームコホモロジーのより直接的な計算方法を紹介したいと思います。
常々思っているのですが、ブログを書いて公開することによって、自分自身が一番勉強になっています。
タイムラインに僕より専門的な数学に詳しい人がたくさんいるので、記事に書くと「こんなのありますよ!」というのを教えてくださるのが嬉しい。
— tsujimotter 日曜数学者 (@tsujimotter) 2021年2月18日
書けば書くほど僕自身が勉強になるポジティブフィードバックが出来ています。大変ありがたい話です。
私自身は独学で数学を勉強しているので、本に書いてない内容についてはただただ自分の頭で考えるしかないのですが、どうしてもわからずに断念してしまうことが多々あります。なので、私の知らないアイデアをより詳しい人に提供いただけるのは、本当にありがたいことです。
独学で数学を勉強していて、私と同じように悩んでいる人はいるのかもしれません。私のケースがどれぐらい一般化できるのかは分かりませんが、「自分がここまで理解したぞ」という部分を、ブログなりSNSなりで(理解が完全でないことを承知の上で)アウトプットしてみるというのも悪くはないのではないかなと思っています。*1
今後もこういったコミュニケーションを大事にしながら、勉強を進めていきたいと思っています。
それでは内容に入っていきましょう!
復習:グリーンの定理
今回もやはりグリーンの定理を使うことになります。定理の主張をおさらいしましょう。
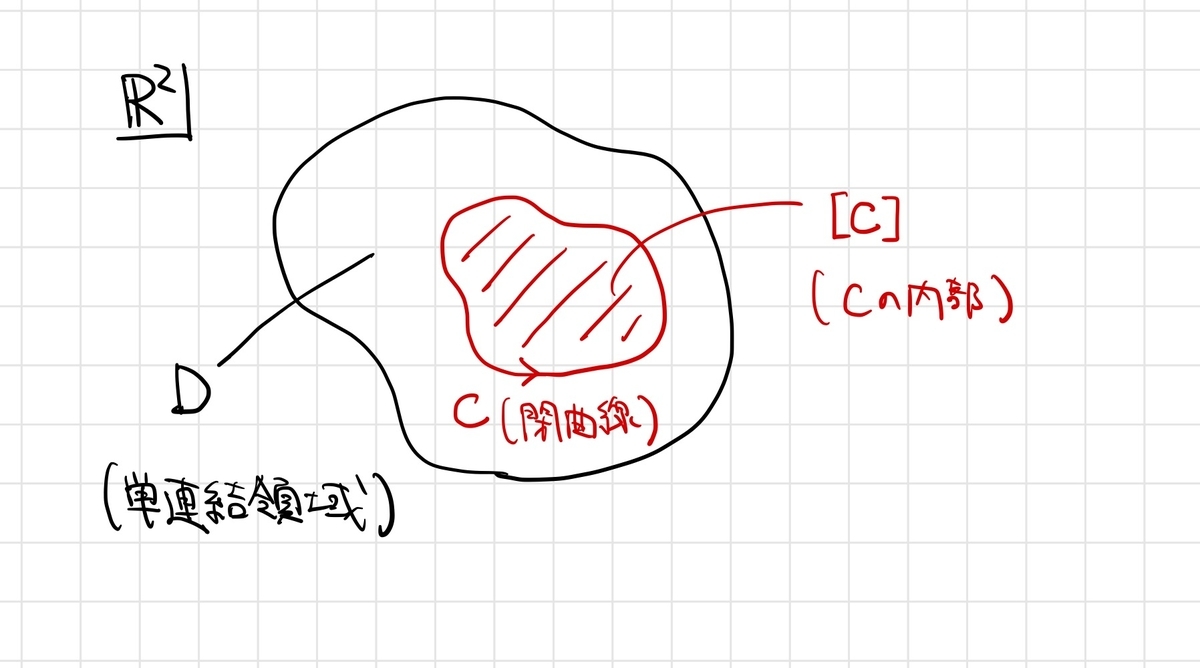
単連結な領域内で、ぐるっと一周回る経路(閉曲線)を考えると、その上の線積分が右辺の積分で計算できるというわけですね。そして、特に「閉1形式」の条件
を満たせば、右辺の被積分関数が になるので、積分全体も
になります。
すなわち、式 の条件を満たせば、単連結な領域
の中での閉曲線の積分は、どんな経路を通ったとしても
になるということですね。
また、線積分の被積分関数を、微分1形式の形で
と表したとします。ここで、 が
上の
級関数であるとき、
を
上の
級1形式といいます。
外微分の定義 より、上のグリーンの定理は
であるということを主張しているわけですね。
特に、 が閉1形式であるとき(式
を満たすとき)、
より
が成り立つということです。
単連結ではない領域に拡張
ここからが新しい内容なのですが、実はこのグリーンの定理、単連結ではない領域であっても使うことはできます。
「何を言っているんだ。定理の条件は単連結な領域だろう」と思うかもしれません。

もちろん、単連結ではない領域でもそのまま成り立つと言いたいのではありません。ちょっと違う形で活用できるといっているわけですね。具体的には、グリーンの定理から次の系を導きたいと思います。
このとき、 上の
級1形式
が閉1形式である(すなわち、
を満たす)ならば、次の等式が成り立つ:
系2の証明に行く前に、主張の内容を確認します。
まず、 が単連結とは限らない領域であることに注意しましょう。また、単純閉曲線とは自身と交わらない閉じた曲線のことです。自身と交わらないことによって、曲線の内部と外部に分けることができます。
「 が
の内部に含まれる」ということで、条件を満たす
としては、たとえば次のような状況になります:
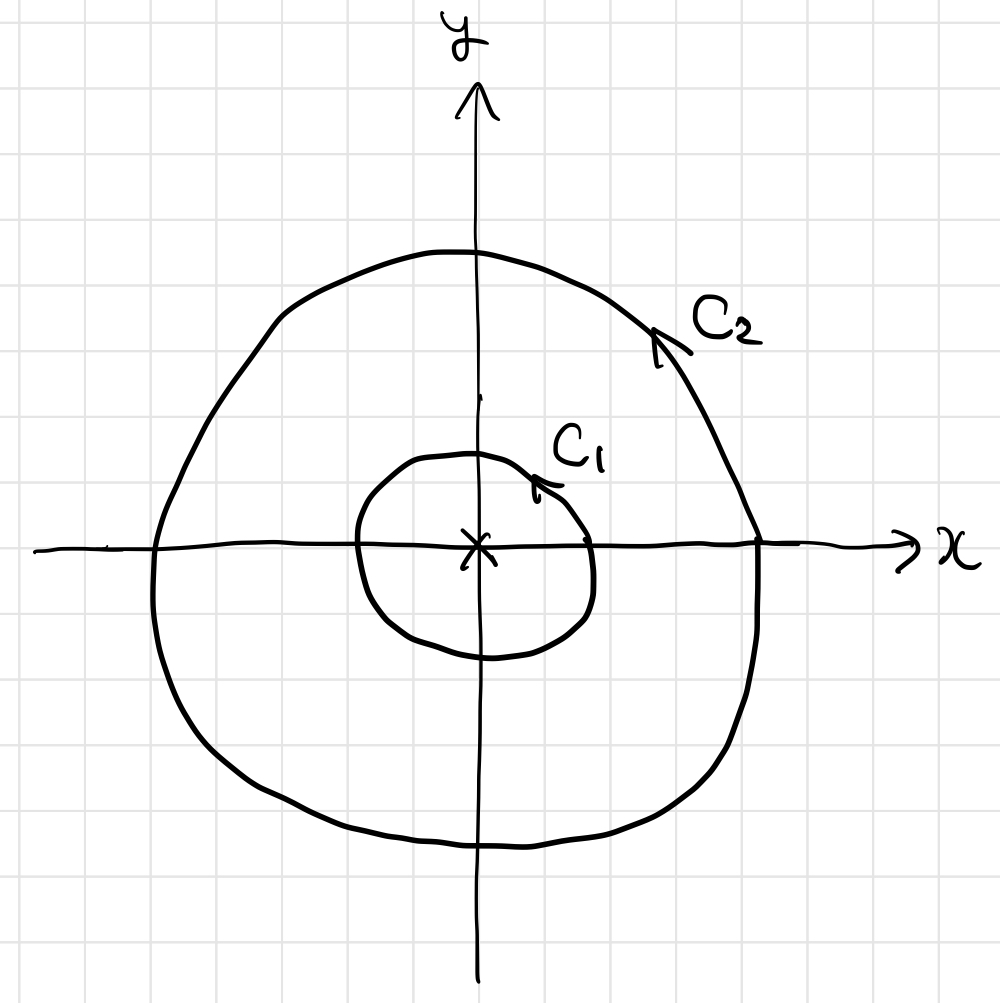
このとき を周る積分と
を周る積分が等しい、というのが定理の主張ですね。つまり閉曲線の積分は、原点の周りを左回りに1周しているのであれば、経路によらないということを主張しています。
前節で述べたように、 が原点も含めて
級であり、かつ閉1形式であれば、穴の空いていない単位開円板
上でグリーンの定理を使うことで、積分値が
となります。よって、特に
上の積分値と
上の積分値は一致しますね。
問題は が原点で条件を満たさないときです。この場合は、条件を満たす領域として原点を含むものを考えることはできませんので、
を用いることになります。しかしながら、
は単連結ではないので グリーンの定理はそのままでは使えない。どうしようか、というわけですね。
単連結ではない領域の場合に、グリーンの定理を応用するにはどうしたらよいでしょうか。アイデアはこうです。単連結な領域がなければ、作ってしまえばいい のです。
まず、上のように を考えます。

ここで次のような2つの積分経路を考えたいと思います。

と
を結ぶ「橋」のような経路があります。
- 赤い経路
は、
の上半分を通りつつ、橋を渡って
の上半分を逆回りに通る経路
- 青い経路
は、
の下半分を通りつつ、橋を渡って
の下半分を逆回りに通る経路
赤い経路 と青い経路
を足すと、ちょうど橋を通るときの向きが逆になっていて、積分が相殺されます。したがって
が成り立ちます。
ここで 赤い経路 と青い経路
に着目すると、それぞれが単連結な領域となっていますね! ここでグリーンの定理を使うのです!!
グリーンの定理より、 ですから
が成り立つわけですね。結局
ということになります。
上では、
しかしながら、 が交差する場合も考えたいと思うかと思います。たとえばこんな状況です。
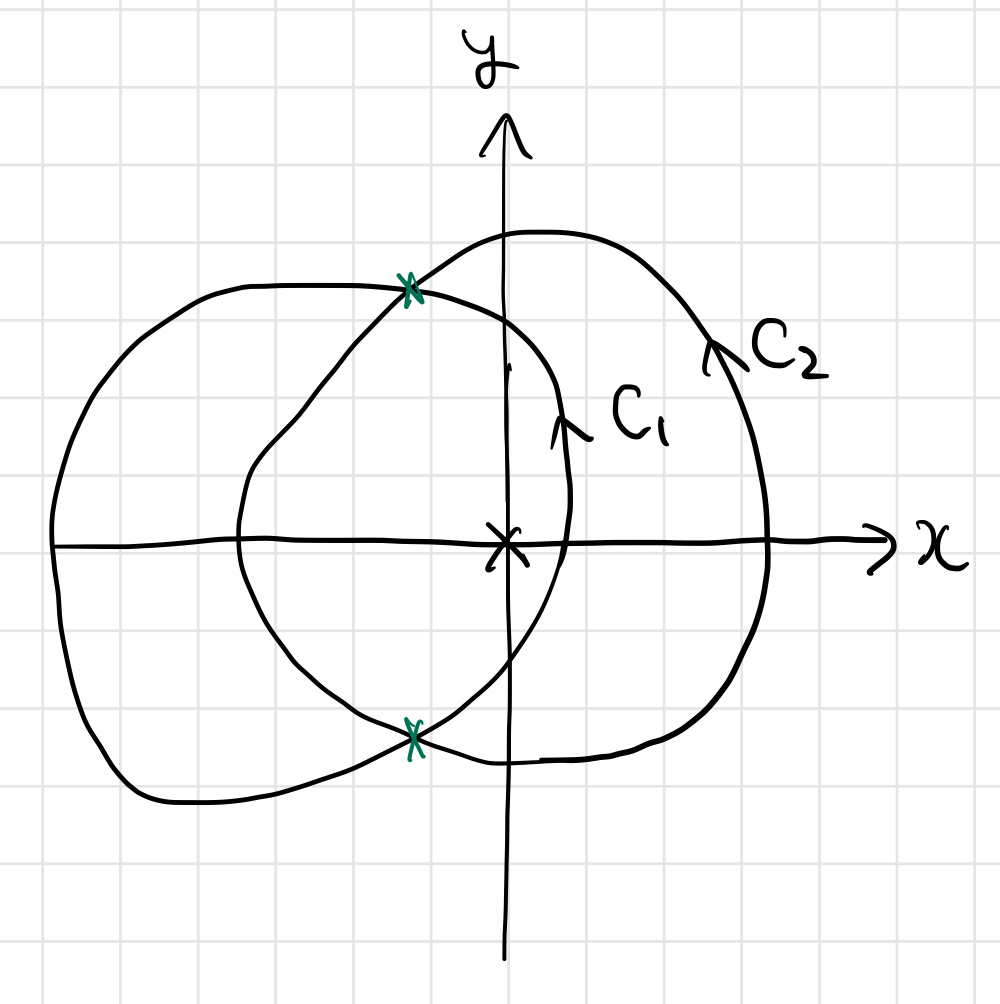
この場合は の交点で経路を切り分けます。今回の場合は、左右に2つの閉路ができますので、両者にグリーンの定理を適用すればOKです。
こういう色々なパターンに対して細かい議論をしていく必要がありそうですね。
ド・ラームコホモロジーの計算
さて、ようやく本題のド・ラームコホモロジーの計算を実行したいと思います。
長々と議論してきたように、 上の
級1形式
であって、閉形式
、言い換えると
を満たすものについて、原点を左回りに1周する閉曲線 上での線積分
が積分経路 の取り方によらない、ということでした。
そこで、写像 を、
に対して
で定めることにしましょう。つまり、 をぐるっと一周積分すれば値が求まるわけですね。
この は明らかに
上の線形写像となっています。
ここで、次の性質を示すことにしましょう:
閉1形式 に対しての命題です。特に
が原点を左回りに積分して
になるのであれば、
なる
が存在する
なる
が存在すれば、原点の左回りに
を積分すれば
になる
ということを主張しています。
なお、命題3が言えた時点で1次のド・ラームコホモロジーが計算できたことになるので、それを先に議論しておきましょう。
主張より、 が成り立ちます。したがって、1次のド・ラームコホモロジー
の定義と準同型定理より
が成り立ちます。これで1次のド・ラームコホモロジーが計算できたことになります。
それでは、命題3の主張を証明しましょう:
(証明)
( の証明)
より、
内の任意の単純閉曲線で
を積分した値は
になります。たとえ、閉曲線の内部に原点を含んでいたとしてもです。
(これはグリーンの定理の帰結とは無関係に、 がそういう仮定だということですね。)
そこで前回の記事とまったく同じように、始点 を固定して、
から点
への2通りの経路
を考えます。
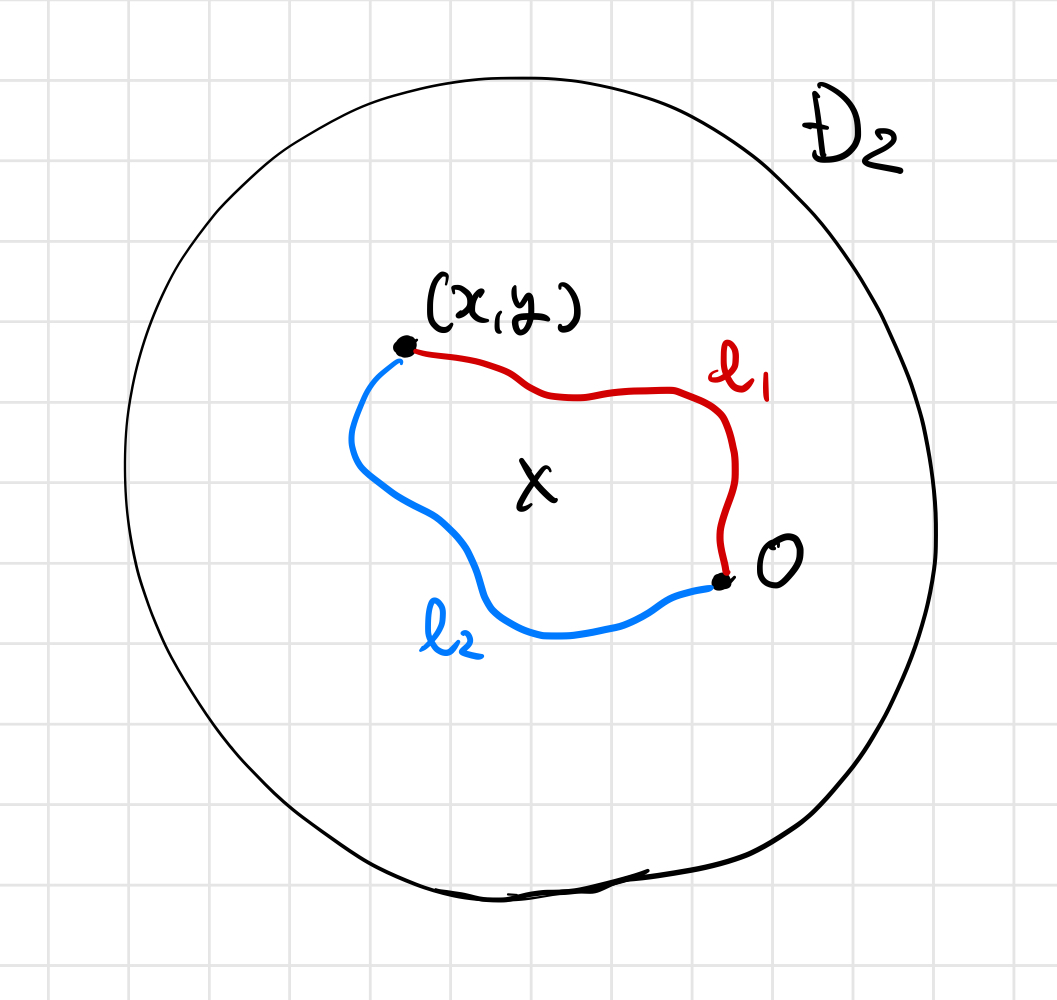
その上で を積分することを考えると、
が閉曲線になることから、
となりますね。よって
となり、始点 を固定したときの点
までの積分が、その経路の取り方によらないことがわかりました。これを
と表します。これを用いて関数
と定義すると、これは 上の
級関数となります。
前回議論したのとまったく同じ方法で も分かります。よって、
は完全1形式
であることが示されました。
( の証明)
は完全1形式なので、ある
上の
級関数
が存在して
が成り立ちます。
ここで、 を半径
を左回りに1周まわる閉曲線をとると、
上の点
は
と表せる。 の1変数関数だと思って
上で
の線積分を計算すると
が成り立ちます。
以上の議論により、 であることが分かりましたが、具体的に
を代表とする類 が
の基底であることを示しましょう。
まず、曲線 を半径
を左回りに1周まわる閉曲線とします。命題3の証明でやったように、
上の点
は
のように表せます。閉曲線 上で
を線積分すると
となります。よって、 より
です。
ここで、任意の に対して、
の属する類
が
の実数倍で表せることを示します。これを示すために
を定義します。
また、 を計算すると、
の線形性より
となり、 であることがわかります。
よって
であるから、 と
は
の同じ類に属します。
つまり、 の任意の類
は、
の
倍として
と表せることがわかりました。
以上により
が示されました。
おわりに
今回わかったことは、( における原点のような)領域から除去した点のまわりを1周する経路を考えて、その上の積分を実行することがド・ラームコホモロジーの計算において本質的であるということでした。今回の計算においては、
がまさにそれでした。
閉形式 を上の経路で線積分したときに、積分値が
になるのであれば特異点まわりの回転の寄与が無視できるわけです。よって、定点
から線積分によって関数
が定義できる。つまり完全1形式であるということですね。こういう関数
は物理的には「ポテンシャル」の意味合いがあるようですね。また、逆に完全1形式なのであれば、同様の経路を積分したときの値は
になる。
よって、(領域から除去した点のまわりの)積分値を計算することで、ド・ラームコホモロジーのどの類に属するのかが決まってしまう というわけです。これはド・ラームコホモロジーを考える上できわめて重要な観点だと思います。
また、前半の話ですが、単連結な領域内でなくとも「うまく単連結な領域のまわりの積分経路を作る」ことで、積分経路をとり変えることができるという面白い考え方を得ましたね。グリーンの定理の適用範囲はこんなに広かったのかと驚きました。
今回の計算は、単なるド・ラームコホモロジーの練習問題に留まらず、本質的な理解の手助けになる有用な問題だったのだなと実感しました。計算方法を教えてくださったラスクさんには改めて感謝申し上げます。
それでは今日はこの辺で!
*1:結城先生による質問回答の内容が大変共感できるものだったので、リンクを共有します。
質問(学んだことを発表したいが未熟をさらけ出すのが不安)
ご質問ありがとうございます。あなたが感じる不安はとてもよく理解できます。そしてその不安をどう扱うかは極めて重要です。(続く)#結城浩に聞いてみようhttps://t.co/CXeXYzO7EF pic.twitter.com/1GwGgN6c4R
