またまた RSA 暗号の関連記事です。記事の中で「一次不定方程式」という概念が登場しましたので、その補足をしたいと思います。
一次不定方程式の整数解：
を互いに素な整数としたとき，以下の方程式を満たすような整数解
が存在する．
この一次不定方程式の整数解を求める問題、ちょっとだけとっつきにくい印象があるのですが、視点を考えれば非常にわかりやすくなることに気づきました。
実はこれ「油分け算」と言われる問題とまったく同じなのです。
油分け算とその解き方
「油分け算」って何だっけ？
と思う方でも、この問題は聞いたことがあるでしょう。
3ℓと 5ℓの升（マス）があります。
この２つの升を使って、1ℓの油を計り取ってください。
油分け算は「塵劫記」と呼ばれる江戸時代の数学書に登場した有名な問題です。当時は「数学」ではなく「和算」の時代でした。
よく使われる例題では、1ℓではなく 4ℓを計り取るものでしょう。結局、同じ問題であることが後で分かるので、まずは 1ℓから考えます。
ちょっと暗算すればわかります。
と、
は、差がちょうど になります。したがって、
ℓの升で
回計りとってできた
ℓから、
ℓの升で
回すくいだしてあげれば
ℓのできあがりです。
油分け算は一次不定方程式で表せる
上で挙げた計算を数式で表してあげましょう。 ,
とおくと、
となります。これは、上で述べた一次不定方程式の解に を代入して出来た式に他なりませんね。
結局これで、「油分け算」と「一次不定方程式の整数解を求める問題」が等価であることがわかりました。
上の一次不定方程式は、大きさが ,
という二つの升を使って、
を計り取るためには、
の升を
回、
の升を
回使う必要があるということを意味しています。ただし、
は正にも負にもなり得ますが、正の場合は「油をすくい加える」、負の場合は「油をすくい出す」ことに注意です。
図にすると、こんなイメージです。
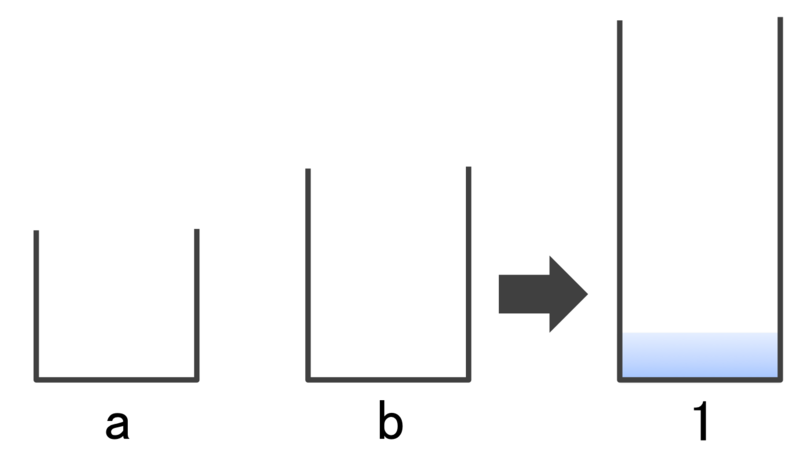
3ℓと4ℓで「任意の整数ℓ」の油をつくる
ここで、冒頭で述べた「なぜ 4ℓをつくるのも 1ℓをつくるのも同じなのか」という点に触れておきましょう。「 ℓつくることができれば、
ℓもつくることができる」といった方が正確でしょう。
上の手順で ℓを作ります。すると、式で表すとこうなりますね。
ただし、,
としています。
ここで、両辺を 倍しましょう。すると、
こうなります。この式の意味するところは、つまりこういうことです。
「 ℓの升で油を
回すくい加え，そこから
ℓの升で油を
回すくい出せば，油
ℓが得られる」
したがって、 ℓが得られました。
同様に、 ℓを作りたければ、両辺
倍すればよいわけですから、
ℓの升と
ℓの升を用意すれば、「任意の整数 ℓ」の油をつくることができますね。
最大公約数
ℓと
ℓの升ではすべての整数をつくることができましたが、ほかの大きさの升だとどうでしょうか。
たとえば と
では、「
の倍数」しか作れそうにありませんね。
これについては、すでに初等整数論によって結論が出ています。
最大公約数 (GCD) を使います。
最大公約数（GCD）：
あるいは単位
のように表す．
最大公約数の例を挙げると、こんな感じです。
ちなみに、 の最大公約数が
になるとき、
と
は互いに素である、というように言います。上の例では、
と
は互いに素ですね。
この最大公約数を使うと、一次不定方程式に解が存在する条件は、以下のように表せます。
一次不定方程式の整数解（一般的な例）：
冒頭でに挙げた例で、右辺が となっていたのは、
の最大公約数が
、すなわち
と
が互いに素だったからなのですね。
ちなみに、，
の例では、
となって、たしかに 「 の倍数しか作れない」と言っていた、先ほどの直感とあっていますね。
おまけ：なぜ「一次不定方程式」と呼ぶの？
最後におまけとして、今回使った方程式が、なぜ「一次」「不定」方程式なのか、という点に触れて終わりたいと思います。
「一次」であるのは、方程式の解 ,
の肩に 2乗や3乗のような指数がついていなくて、1乗になっているからです。こういう方程式を「一次方程式」と呼びますよね。
では、「不定」なのはなぜか。 としたときの一次不定方程式は、
となりますね。
たとえば、方程式の解 を整数に限らないとして、その解は１つに定まるでしょうか。定まりませんね。
なら
だし、
なら
です。片方が定まらないと、１つに決まりません。あるいは、連立方程式のように式を加えても良いかもしれませんが、式がもう１つないと定まりませんね。
このように、解が一意に定まらないような方程式を「不定」方程式と呼ぶのです。だから、「一次」「不定」方程式なのでした。
単なる不定方程式だったら、あまり意味のある結論は出ないのですが、もし「解を整数に限れば」ある程度秩序だった知見を導き出す事が出来ます。それが、一次不定方程式の「整数解」というわけです。
たとえば、先ほどの例だと、
の方程式のままでは、単に と
の関係を表しただけで、これ以上先に進めません。
もし解 を整数に絞れば、
のように意味のある結論を導くことが出来ます。
以上、豆知識でした。今日はこの辺で終わりたいと思います。それでは。
関連記事
この文章を書くきっかけとなった記事です。RSA 暗号って整数論がぎっしり詰まっていますよね。
RSA 暗号がようやく分かった気がしたのでまとめてみる - tsujimotterのノートブック
ちょっと難度が上がりますが、最後の証明について関連する話が以下の記事に書いてありますので、興味を持った方はどうぞ。
独習ノート「素数と２次体の整数論」＃３：Z のイデアル (2/2) - tsujimotterのノートブック
