リーマンの素数公式を可視化する - tsujimotterのノートブック

三行でまとめると

《リーマンの素数公式》 を可視化するブラウザアプリを作りました。

面白いから使ってみてね。

解説もあるよ（以下ずっと続きます）。

はじめに

《リーマンの素数公式》 は、１９世紀を代表する数学者ベルンハルト・リーマンが、論文「与えられた数より小さい素数の個数について」の中で証明した

素数の個数を厳密に計算する「魔法の公式」

です。

この論文は、幾何学や複素関数論で著名なリーマンが「素数」について書いた「唯一の」論文です。内容は非常に簡潔でたった８ページしかありません。英語版は今でも以下のリンクから読むことができます。

Riemann, B. (1859), "On the Number of Prime Numbers less than a Given Quantity."

本記事では、リーマンの遺した魔法の公式の全貌を明らかにするとともに、その公式を「目で見る」ための方法を紹介します。

以下、記事全体の３／４ぐらいを使って、「《リーマンの素数公式》 とは何なのか」を丁寧に解説していきます（解説編）。

残り１／４の「ブラウザアプリつくりました」 の項で、この《リーマンの素数公式》 を目で見るために作った tsujimotter の自作アプリを紹介します。
アプリを使ってみたいだけの人は、「ここ」まで飛んで読み始めても大丈夫です。

この記事は tsujimotter が以前書いた「ガウスの素数定理」から続くお話です。よろしければ、合わせてこちらもご覧ください。

想定する読者

大学の数学はまじめに勉強し、趣味で数学の啓蒙書を読んでいるうちに 《リーマンの素数公式》 に興味が沸いてきた。けれども、Wikipediaの解説じゃ物足りない。もっと詳しく知りたいよ。そう考えている「あなた」のための記事です。

《リーマンの素数公式》 を自分で計算してみたいという「奇特な」方にも役に立つ内容になっているかと思います。

背景

さて、ここからが解説編です。

話はガウスが発見した「素数定理」から始まります。
（素数定理については、以前の記事ガウスの素数定理でまとめています。）

ガウスの素数定理は、以下の２点について主張する定理です。

素数の出現は確率によって表現される
1. を使えば $x$ 以下の素数の個数を計量する関数（以下、個数関数）である $\pi(x)$ は、対数積分 ${\rm li}(x)$ によって「だいたい」近似できる

素数定理は、数学者が長年追い求めてきた「素数の秘密」に迫るための重要なツールとなっています。

たしかに素数定理を使えば、素数のことは「ざっくりと」わかるでしょう。

でも、考えてみてください。「素数であるか」「素数でないか」は確率事象ではないのです。2, 3, 5, 7, ... は素数であって、6, 8, 10, ... は素数ではない。これは未来永劫変わりませんよね。「サイコロを振ったら7 が合成数になる」なんてことはありません。

確率に頼らずに、個数関数そのものを「厳密に」表現するような公式がほしいですよね。
もっと別の、たとえば「素数を数えなくても、ずばっと素数の個数がわかっちゃうような」そんな「魔法の公式」はないのでしょうか。
それこそが「素数の秘密」を解き明かすのにはふさわしい公式だと思いませんか。

そんな公式、あったらいいですよね。

それが 《リーマンの素数公式》 です。

リーマンの素数公式とは

《リーマンの素数公式》 の書き方はさまざまありますが、今回は以下のように表現してみましょう。

《リーマンの素数公式》

$\displaystyle \pi(x) = {\rm R}(x) + \sum_{k=1}^{\infty}{\rm T}_k(x) + {\rm I}(x)$

等号を挟んで左辺が求める個数関数。右辺が３つの関数で構成される和。両辺を結ぶ等号は、それらが「厳密に等しい」ことを表しています。

右辺の第一項 ${\rm R}(x)$ は、《リーマンの関数》という名前がついています。この項は、「主要項」とも呼ばれ、《リーマンの素数公式》 の中核を担っています。

第二項は、《振動項》 と呼ばれます。なぜ 《振動項》 なのかは、後にわかるでしょう。この項は、Σ記号を使った ${\rm T}_k(x)$ という関数の無限和になっています。なので、残念ながら、すべての和を計算することは、少なくとも計算機の上では困難であると思ってください。

でも、安心してください。Σ記号の部分の和を無限に取らなくても、 $k$ を小さいほうから順に部分的に和をとっていけば、ある程度の $k$ で、その部分和は終着点の近くに落ち着きます。これを数学用語で「収束」といいますが、もちろん今回の和も「収束」します*1。しかも、その「収束」のスピードは結構速いです。

最後に第三項ですが、これについては今回の記事では扱いません。なぜなら、いずれの $x$ に対しても、 ${\rm I}(x)$ はほとんどゼロに近い値を取り、第一項・第二項ほどの影響を及ぼさないからです*2。

というわけで、ここから先は第一項・第二項の解説に専念していきましょう。

素数公式の第一項（主要項）と《リーマン関数》

まずは主要項からみてみましょう。「主要項」という名前だけあって、この項だけで個数関数のかなりの部分を近似することが出来ます。

主要項の定義を見る前に、その近似の能力をグラフで拝んでおきましょう。

f:id:tsujimotter:20140628180239p:plain

横軸が $x$ で縦軸が関数値。青色の線が求めたい個数関数 $\pi(x)$ , 赤色の線が 《リーマン関数》 ${\rm R}(x)$ となっています。

見てください。このグラフを。

個数関数と、ほぼ一致しているではありませんか！

個数関数はその形状から、別名「素数階段」と呼ばれますが、階段のようにギザギザと上っています。それに対して、 《リーマン関数》 は、そのギザギザの合間を縫うように、一直線に進んでいます。

ガウスの素数定理のときの図と比べると、違いは一目瞭然です。

ガウスの対数積分は、横から素数階段を眺めているだけでしたが、リーマン関数は階段の真上を上っています。

さて、こんな素敵な主要項は、一体どんなお顔をしているのでしょうか。

主要項を構成する 《リーマン関数》 の定義をみてみましょう。

《リーマン関数の定義》

$\displaystyle {\rm R}(x)=\sum_{1\leq m\leq \log_{2}(x)} \frac{\mu(m)}{m} {\rm li}(x^{\frac{1}{m}})$

なかなか厳めしい顔をしているように見えるかもしれませんが、よくよくみていくとそれほど難しいものではありません。

$\mu(m)$ はメビウス関数で、 ${\rm li}(x)$ はガウスの素数定理にも登場した対数積分です。

《リーマン関数》 の右辺は、無限和のように見えますが、実は有限です。

和の条件は

$1\leq m \leq \log_2(x)$

なので、たとえば引数が $x=100$ だったとすると

$1\leq m \leq \log_2(100)\simeq 6.64$

より、 $m=1, 2, 3, 4, 5, 6$ だけを考えればよいことがわかります。

この場合、メビウス関数の値は知られていますので、次のように簡潔に表せます。

$\displaystyle {\rm R}(x)=\frac{{\rm li}(x^{\frac{1}{1}})}{1} - \frac{{\rm li}(x^{\frac{1}{2}})}{2} - \frac{{\rm li}(x^{\frac{1}{3}})}{3} + 0 - \frac{{\rm li}(x^{\frac{1}{5}})}{5} + \frac{{\rm li}(x^{\frac{1}{6}})}{6}$
（ただし、 $2^6\leq x< 2^7$ ）

上式のように書き下すと簡単に見えますね。対数積分を上の式で変換するだけで、こんなに精度を上げられるのです。

しかしながら、いくら近似精度が高くてもあくまで近似でしかありません。

私たちの目標は個数関数を「厳密に」再現することです。たとえば、主要項だけでは「ギザギザの部分」を再現することはできませんね。

厳密な個数関数を再現するために必要なのが、次で述べる第二項というわけです。

素数公式の第二項（振動項）のふるまい

上のリーマンの素数公式とはで述べたように、第二項は無限和の形になっています。

$\displaystyle \sum_{k=1}^{\infty} {\rm T}_k(x) = {\rm T}_1(x)+{\rm T}_2(x)+{\rm T}_3(x)+...+{\rm T}_k(x)+...$

すなわち、これらの無限個の関数*3の和になっています。

関数の無限和というと、大学で数学を多少かじった人なら、《テイラー展開》や《フーリエ展開》を思い浮かべるかもしれません。

実を言うと、今回のこの式はまさに《フーリエ展開》なのです。とてもそうは見えないかもしれませんが。笑

《フーリエ展開》とは、複数の周波数の音が混ざった中から、周波数毎の音に分解するような変換式のことでした。

マーカス・ソートイの著書「素数の音楽」では、素数公式の振動項は「音」に例えられます。 ${\rm T}_1(x) , {\rm T}_2(x), {\rm T}_3(x), ...$ という異なる楽器の音色が無限に合わさって、「素数の階段」という「ハーモニー」を形作っているのだそうです。

音楽の例えはさておき、果たしてこの無限和は、主要項を「素数の階段」に近づけるのに役立つのでしょうか。
リーマン関数は、たしかに素数階段の上をきれいに上っていましたが、それでもところどころ階段特有のギザギザが張り出していて、その点が誤差を生んでいました。

この誤差を埋めることは、はたしてできるのでしょうか。

試しに ${\rm T}_k(x)$ を主要項に加えてみましょう。

まずは、 $k=1$ の T_1(x) を加えてみます。

《リーマンの素数公式： $k=1$ まで》
$\displaystyle {\rm R}(x) + {\rm T}_1(x)$

このときのグラフは以下のようになります。

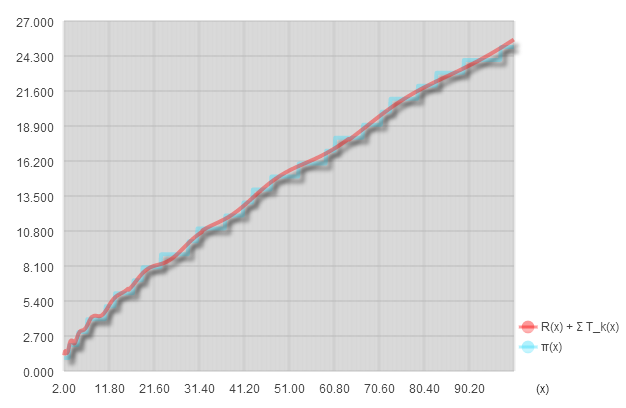
いかがでしょうか。
少しうねりが加算されて 《リーマン関数》 が動き始めました。

このままだと、まだよくわかりませんね。

続けて $k=2, 3, 4$ と項を加えていきましょう。

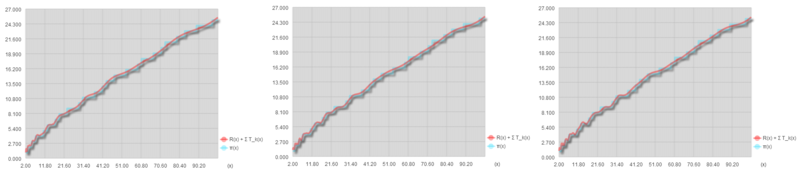
$k=4$ までくると、下の方の階段はずいぶんと再現されてきたのではないでしょうか。

一気に $k=20, 50, 100$ まで足した結果を見てみましょう。

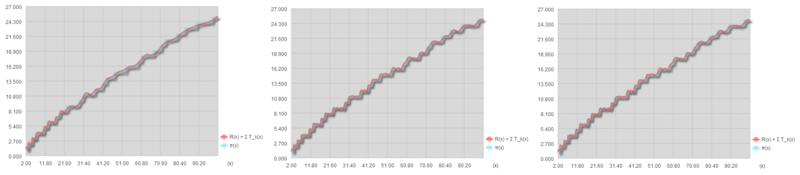
たしかに $k$ を増やすことで、目標とする「素数の階段」に近づいていくことが分かります。

$k=1$ のときの「振動」を、単体で取り出してみると次の図のようになります。

f:id:tsujimotter:20140628222734p:plain:w400

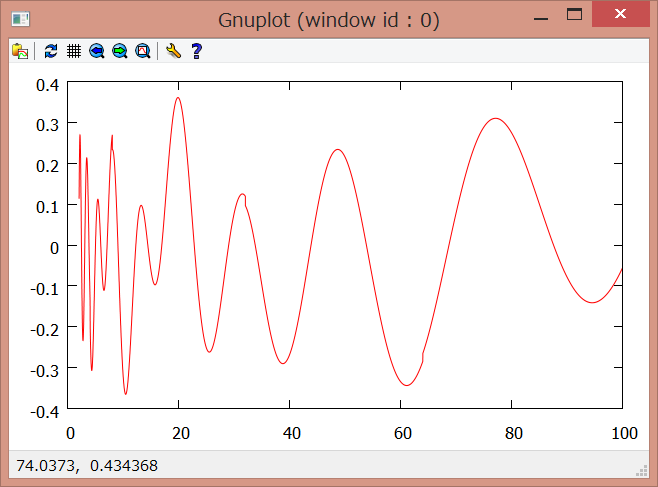
数々の「振動」が重なって、素数の階段を作っていたのですね。そのため、これらの項を 《振動項》 と呼んでいます。

すると今度は「この振動項とはいったい何なのか」という疑問が浮かんできます。次の節では、いよいよこの 《振動項》 の正体に迫っていきましょう。

振動項の正体とゼータ関数の零点

まずは、《振動項の定義》を紹介しましょう。

《振動項の定義》

$\displaystyle {\rm T}_k(x) = -\sum_{1\leq m\leq \log_{2}(x)} \frac{\mu(m)}{m} \{ {\rm li}(x^{\frac{\rho_k}{m}}) + {\rm li}(x^{\frac{\bar{\rho_k}}{m}}) \}$

この式に登場する $\rho_k$ や $\bar{\rho_k}$ は一体何でしょう。これこそが、 《振動項》 の「核」である 《ゼータ関数》の非自明な零点です。

ガウスの素数定理に引き続き 《ゼータ関数》 が再び登場しましたね。この記事では、ゼータ関数の一部（ $\zeta(1)$ ）を使って素数定理を証明したのでした。

今度は、ゼータ関数の 《非自明な零点》 を使うことになります。

ここで 《零点》 とは「ゼータ関数の値が 0 に等しくなるような引数」のことです。
《零点》 は、言わばその関数を表す「ID番号」のようなものです。

《ゼータ関数の零点》 を式を使って次のように表すことができます。

《ゼータ関数の零点》

$\zeta(\rho) = 0$
となるような複素数 $\rho$ をゼータ関数 $\zeta(s)$ の零点という。
ただし、 $\zeta(s)$ は $s=1$ 以外の複素数平面全域に解析接続されたゼータ関数とする。

《振動項》 の式で登場する $\rho_k, \bar{\rho_k}$ は、零点の中でも特に 《非自明な零点》 と呼ばれています。

《非自明な零点》

実軸の負の偶数上の零点を 《自明な零点》 といい、それ以外の零点を 《非自明な零点》 という。

以降、虚軸正方向の非自明な零点を、実軸に近い順に $\rho_1, \rho_2, \rho_3, ..., \rho_k, ...$ と表記する。同様に、対応する虚軸負方向の零点を $\bar{\rho_1}, \bar{\rho_2}, \bar{\rho_3}, ..., \bar{\rho_k}, ...$ とする。

いろいろ難しいことを書きましたが、結局のところ

《ゼータ関数》 をゼロにするような複素数（つまり 《零点》 ）を集めて、それを 《振動項》 の指数に代入して計算すれば良い

のです。
《零点》 は必ず実軸に対して対称に存在しますので、共役な組をセットにして和をとっていきます。

《非自明な零点》 の多くは既に知られています。
たとえば、以下のサイトでは、原点に近い順に 100000 個の 《非自明な零点》 の組の座標がまとまっています。

Andrew Odlyzko: Tables of zeros of the Riemann zeta function

上のサイトのデータを元に、原点周辺の 《零点》 を表したものが次の図です。横軸が実部、縦軸が虚部を表す複素数平面です。

f:id:tsujimotter:20140628223653p:plain:w400

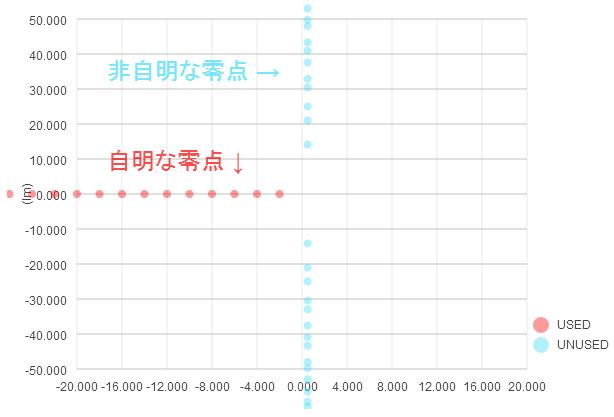
上の図からわかる通り、《非自明な零点》 は $\rho_k, \bar{\rho_k}$ は複素数です。
したがって 《振動項》 の計算においては、複素数の指数関数を計算しなければなりません。

複素数のべき乗計算は想像以上に厄介です。*4

そこで、どうにかして 《振動項》 の計算を「実数のまま」行いたいのです。最終的に計算される値は（うまく重なって）実数になる訳ですから、実数のまま計算する方法はありそうです。

《振動項》の計算法とクリティカルストリップ

「《振動項》 を実数のまま計算できないかなぁ」と考えていたところ、ちょうど良さそうな論文を発見しました。探せばあるもんですねぇ。

H. Riesel and G. Göhl, "Some Calculations Related to Riemann's Prime Number Formula", Mathematics of Computation, Vol.24, No.112, pp. 969-983 (1970).

この文献によると 《とある仮定》 が成り立てば、 《振動項》 の計算を実数のまま行えるようです。簡単になった 《振動項》 の式は次のものです。

《H. Riesel と G. Gohl の式》

$\displaystyle \{{\rm li}(x^{\rho_k})+{\rm li}(x^{\bar{\rho_k}})\}\simeq\frac{2\sqrt{x}}{|\rho_k|\ln(x)}\cos\left( \alpha_k \ln(x)-\arg(\rho_k) \right)$

$\rho_k$ は、実軸対称な 《非自明な零点》 のペアの片方（虚部が正の方）を表しています。

この式を見ると、確かに $\cos$ を含んでおり「振動」項という感じがしてきました。 《フーリエ展開》 に見えなくもない（？）ですね。

たとえば、原点に最も近いの 《非自明な零点》 のペアは次のものです。

$\displaystyle \rho_1 = \frac{1}{2}+i\cdot 14.134725$

$\displaystyle \bar{\rho_1} = \frac{1}{2}-i\cdot 14.134725$

これを 《H. Riesel と G. Gohl の式》 の式に代入したものが、先ほどの k=1 のときの 《振動項》 のグラフだったわけです。

ところで、先ほど挙げた 《とある仮定》とは、具体的には次の仮定のことです。

《とある仮定》

$\displaystyle \rho_k = \frac{1}{2}+i\alpha_k$

たしかに、先ほどの図の分布を見る限りでは「どの 《非自明な零点》 も実部は 1/2 に一致する」ように見えます。「実部が 1/2 となるような（複素数平面上の）直線」のことを専門用語で 《クリティカルストリップ》 といいます。

この仮定が真であるか、偽であるか。これにはまだ決着がついていません。

仮定が真であることは、今回の簡単な計算が有効であることを保証するだけでなく、素数の理論にとって重要な意味を持っています。
詳しくは解説しませんが、この仮定が成り立つことで「素数の分布は偏っていない」ことが保証されるのだそうです。

解説のまとめ

長くなってきたので、解説編の部分だけいったんまとめます。

《リーマンの素数公式》 は、《主要項》 と無限個の 《振動項》 の和で構成されています。

まず 《主要項》 は、素数階段の上を通過するように個数関数を精度よく近似します。次に 《振動項》 を加えていくことで、ギザギザした階段の形状に少しずつ近づきます。最終的には収束して、個数関数に厳密に一致するのです。

振動項は、ゼータ関数の 《非自明な零点》 の実軸対称な組にそれぞれ対応してるのでした。 《非自明な零点》 の 《クリティカルストリップ》 上の配置のパターンが、個数関数のギザギザな階段パターンを決めているのです。

要するに、《リーマンの素数公式》 は「素数の分布」を「ゼータ関数の 《非自明な零点》 の分布」という、まったく別の概念に対応づける「魔法の公式」だったわけです。

零点の性質がわかれば、素数のことがわかる。
素数の分布は未だわからないことだらけですが、ゼータ関数の零点にはよく知られた際立った性質があります。
「 《非自明な零点》 は 《クリティカルストリップ》 上にのみ存在する」というものです。残念ながら、この性質は未証明ですが、もし正しければ素数公式を通して「素数の分布は偏っていない」ことが保証される訳です。

素数公式は、古代ギリシャからつづく数学者の素数へのアプローチを、根本から覆すリーマンの新兵器でした。
現代数学における素数理論では、素数公式はなくてはならないものとなっているのです。

ブラウザアプリつくりました

「零点の秩序ある振る舞いが、素数の分布の性質を創り出す」という素数公式の理念に、tsujimotterは数学の美を感じます。公式を計算してみると、その美しさがよくわかります。

素数公式を調べていくうちに「この感動を伝えたい」という思いが溢れてきました。
そこで、みなさんに素数公式の美しさを伝えるために、思い切ってブラウザアプリを作ることにしたのです。

ブラウザアプリのタイトルは「リーマンの素数公式を可視化する」です。
以下のリンクから体験することができます。

リーマンの素数公式を可視化する

本記事の解説編に登場したいくつかのスクリーンショット。気になった方もいるかもしれませんが、すべてこのブラウザアプリで描画したものです。

記事内では数個のパターンしか描画していませんが、このアプリでは k=1 から 1000 までのパターンを描画することができます。
k の数は画面下のボタンをクリックして増やすことが可能です。

f:id:tsujimotter:20140628232652p:plain

画面右側では、現在どの零点の組を使用して素数公式を計算しているかがわかります。

使用する零点の数が増えるに従って、だんだんと個数関数に近づいていくようすが見て取れます。この辺りの面白さは実際に見てみないと分からない感覚だと思います。

零点が作る素数のハーモニーを、ぜひみなさんも体験してみてください。

まとめ

素数公式とは、（ゼータ関数の） 《非自明な零点》 が作る「 《振動項》 のハーモニー」が「素数の階段」を形づくることを表現した芸術的な公式です。

その美しさ・面白さを伝えたくて、今回の記事とブラウザアプリを作ってみました。

「数学者は知っているが、私たちは知らない数学の美しさ」があります。

数学者は数式をみれば理解でき、満足してしまうのかもしれません。
しかしながら専門家ではない一般人は、数式を見ても、その深い意味を理解し美しさを感じとることが（少なくともすぐには）できません。

これまで数学者が感じてきた「数式の美しいところ・面白いところ・感動を呼ぶところ」を、一般人でも体感できるようにしたいと思い、この記事を執筆しました。記事を書いていううちに、このような感動を味わってもらうことは結構大事なことなんじゃないか、と思うようになりました。

tsujimotter は数学が大好きで、かつ、情報系の技術者です。

こうした、ある種の「特殊な立ち位置」を今後も利用して「数学者の視ている世界を、数学者以外も分かるように見せる技術」を作っていけたらと思っています。

あとがき

ところで、素数公式がわかってしまうと、ガウスの素数定理が「微妙」に見えてきたかもしれませんね。

でも、少し考えてみてください。素数定理の必要性はまだ残っています。

素数公式は「ゼータ関数の零点が計算できること」を前提にしています。しかしながら、ゼータ関数の零点の明示的な公式なんてありません。*5

したがって、素数の分布を簡便に計算しようと思うと、やはり素数定理に頼らなければなりません。

近年では 《リーマンの素数公式》 を使って「この素数定理がどの程度信頼に足るものか」という近似精度の測定をしているそうです。
そこには、まとめで述べたように「ゼータ関数の零点がどう分布しているか」が密接にかかわっています。

今回は、「 《非自明な零点》 が 《クリティカルストリップ》 上にのみ存在する」という 《とある仮定》 のもと進めましたが、その仮定が正しいかどうかすらわかっていません。

この仮定が、実は 《リーマン予想》 という100年以上続く未解決問題*6だったのです。

どうです？この分野に興味が沸いてきませんか？

それでは、この辺で。

とてもとても長いこの記事を、最後まで読んでくれてありがとうございます！

参考文献

素数やリーマン予想に興味を持ったあなた！この本を読んでみよう！

明解ゼータ関数とリーマン予想 (KS理工学専門書)

作者:ハロルドエム・エドワーズ
発売日: 2012/06/21
メディア: 単行本（ソフトカバー）

少し難しい専門書ですが、リーマンの素数公式の導出から、リーマン予想へのアプローチまで、何でも載っています。リーマンの論文「与えられた数より小さい素数の個数について」の日本語訳も巻末に載っており、非常にお得です。

「素数の音楽」という本も面白いです。こちらの本は、一般向けに優しく書かれている本です。数式はほとんどありません。「明解ゼータ関数とリーマン予想」は専門的過ぎて難しい、という人でも大丈夫。

素数の音楽 (新潮文庫)

作者:マーカスデュ・ソートイ
発売日: 2013/09/28
メディア: 文庫

素数の音楽で慣れてきたら、多少数式が入ったこの本に挑戦してみるとよいでしょう。
ブラウザアプリ「リーマンの素数公式を可視化する」は、この本を理解するのに十分助けになるでしょう。

素数に憑かれた人たち ~リーマン予想への挑戦~

作者:John Derbyshire,松浦俊輔,ジョン・ダービーシャー
発売日: 2004/08/26
メディア: 単行本

《リーマン予想》 の概略・歴史を理解する上では、NHKのこの動画は傑作と言っていいでしょう。「大人の事情」で削除されてしまわないことを祈ります。
www.nicovideo.jp
www.nicovideo.jp

追記：2016年10月6日

可視化アプリがバージョンアップしました
tsujimotter.hatenablog.com

*1:正確にいうと「条件収束」します。そのため無理やり順番を変えて和を取ると、任意の値に収束させることができてしまいます。ここでは、kを小さいほうから順にとっていきます。

*2:2014/07/03に追記しました。元の記事では上の式に「第三項」の記述はなかったのですが、正確のため後から追加しています。今回の結果にはほとんど影響を及ぼさないなので解説しません。今後気が向いたら触れようかと思います。

*3:名前がついていると話はしやすいのですが。。。

*4:実際、複素関数のべき乗は、複素対数関数と複素指数関数によって計算されますが、対数の値は一意に定まらないため、値が無数に出てしまいます。主値やリーマン面というような、考えたくもない面倒な概念が入ってくるのです。たとえば Ruby という言語には複素数の対数関数を計算するライブラリがありますが、計算値としては勝手に主値が選ばれてしまいます。これが求める計算に合致するかどうかは慎重に検討が必要です。実際私も、このせいで結果が合わず、かなり悩みました。

*5:リーマン・ジーゲルの公式っていうのがあるんですが、ちょい複雑です。

*6:解決すれば、100万ドルもらえます。