#2020になる数式について考えてみた - tsujimotterのノートブック

明けましておめでとうございます！

いよいよ 2020年ですね。2020年といえば、だいぶ前から話題に上がっていたオリンピックイヤーがいよいよやってきたという感じですが、今年はどんな一年になるのでしょうか。良い年にしていきたいですね。

2020年になったということで、毎年恒例の「年号の数についての数式」を考えたいと思います。題して

「#2020になる数式」

です。

Twitterで #2020になる数式のハッシュタグを検索してみると、いろいろな数式が出てきますので、よろしければご覧になってみてください。

#2020になる数式 hashtag on Twitter

今日はtsujimotterが見つけた数式の紹介と、その数式を可視化するWebアプリを作ったのでご紹介したいと思います。

過去の年号の数式については、他の方がまとめてくれたものがありました。よろしければこちらもどうぞ：
2016になる数式まとめ - Togetter
2017を数学的に遊びたおすまとめ - Togetter
2019年新春数学・パズル問題、2019にまつわる性質まとめ - Togetter

2020になる数式たち

「2020」を Wikipediaで調べてみると、こんな数式が見つかりました。

$2020 = 16^2 + 42^2 \tag{1}$
$2020 = 24^2 + 38^2 \tag{2}$
$2020 = 18^2 + 20^2 + 36^2 \tag{3}$
$2020 = 17^2 + 19^2 + 23^2 + 29^2 \tag{4}$
$2020 = 4^2 + 6^2 + 8^2 + 10^2 + 12^2 + 14^2 + 16^2 + 18^2 + 20^2 + 22^2 \tag{5}$

式 $(1), (2)$ は「2つの平方数の和」で2通りに表せるということですね。式 $(3)$ は「3つの平方数の和」です。式 $(4)$ は「4つの連続する素数の平方和」で、式 $(5)$ は「10個の連続する偶数の平方和」です。

2020は、こんなにいろんなパターンの平方数の和で表せるのですね。どれぐらい珍しいかは調べていませんが面白いですね。

実は、2020は少し心配していたのですよね。偶数ですし、あまり面白い性質はないかなと思っていたのですが、何かしら見つかりそうでよかったです。

可視化してみました

というわけで、上の5つの式を可視化するページを作ってみました。
tsujimotter.info

簡単に説明すると、平方数はブロックを正方形に並べて表現することができます。そのため、2つの平方数の和は

f:id:tsujimotter:20200101092645p:plain:w300

こんな風に2つの正方形で表すことができるわけですね。

同様に、10個の平方和はこんな風に表すことができます。

f:id:tsujimotter:20200101092753p:plain:w300

こうやって並べると10連続の偶数である感じが出て綺麗ですね！

上のページでは、アニメーションで数式の形が移りあっていく様子が楽しめますので、ぜひアクセスしてみてください。

なお、このアニメーションは以前私が作った「Primes of the form $x^2 + ny^2$ .」を改造して作ったものになります。こちらもよかったらみてください。
tsujimotter.info

スライドによる解説：
二次形式と素数で遊ぼう - 第２回 #日曜数学会

おまけ：2020は2つの平方数の和で2通りに表せる

上で述べたように、2020は「2つの平方数の和で2通りに表せる」という性質を持っていました。この性質を簡単な計算によって確認したいと思います。

2020は素因数分解すると

$2020 = 2^2 \times 5 \times 101 \tag{6}$

となりますが、 $2^2$ は平方数で、 $5$ と $101$ は $4n+1$ 型の素数です。

よって、それぞれ（0を含む）2つの平方数の和で表せます：

$\begin{align} 2^2 &= 2^2 + 0^2 \\ 5 &= 2^2 + 1^2 \\ 101 &= 10^2 + 1^2 \end{align} \tag{7}$

このような性質は次の「フェルマーの２平方定理」によるものです。

フェルマーの２平方定理（参考）

$p$ を $2$ または $4n+1$ 型の素数とする。このとき

$p = X^2 + Y^2 \;\; (X, Y \text{ は整数}) \tag{8}$

の形で表せる。逆に $p$ が $4n+3$ 型の素数のとき、式 $(8)$ のように表すことはできない。

あとで使いますが、 $p = X^2 + Y^2$ と書いたときの $X, Y$ は、 $\pm X, \pm Y$ と置き換えたとしても、そのまま等式として成り立ちます。よって

$\begin{align} 2^2 &= (\pm 2)^2 + 0^2 \\ 5 &= (\pm 2)^2 + (\pm 1)^2 \\ 101 &= (\pm 10)^2 + (\pm 1)^2 \end{align} \tag{9}$

ということですね。

それでは、これを使って2020の計算をしてみましょう。ここで「ブラーマグプタの恒等式」を使います。

ブラーマグプタの恒等式

$(a^2+b^2)(z^2+w^2)=(az+bw)^2+(aw−bz)^2 \tag{10}$

これは「2つの平方数の和 $a^2+b^2$ 」と「2つの平方数の和 $z^2 + w^2$ 」を掛け合わせて、新しい「2つの平方数の和」を作れる恒等式だと思うことができます。

f:id:tsujimotter:20200101082928p:plain:w200

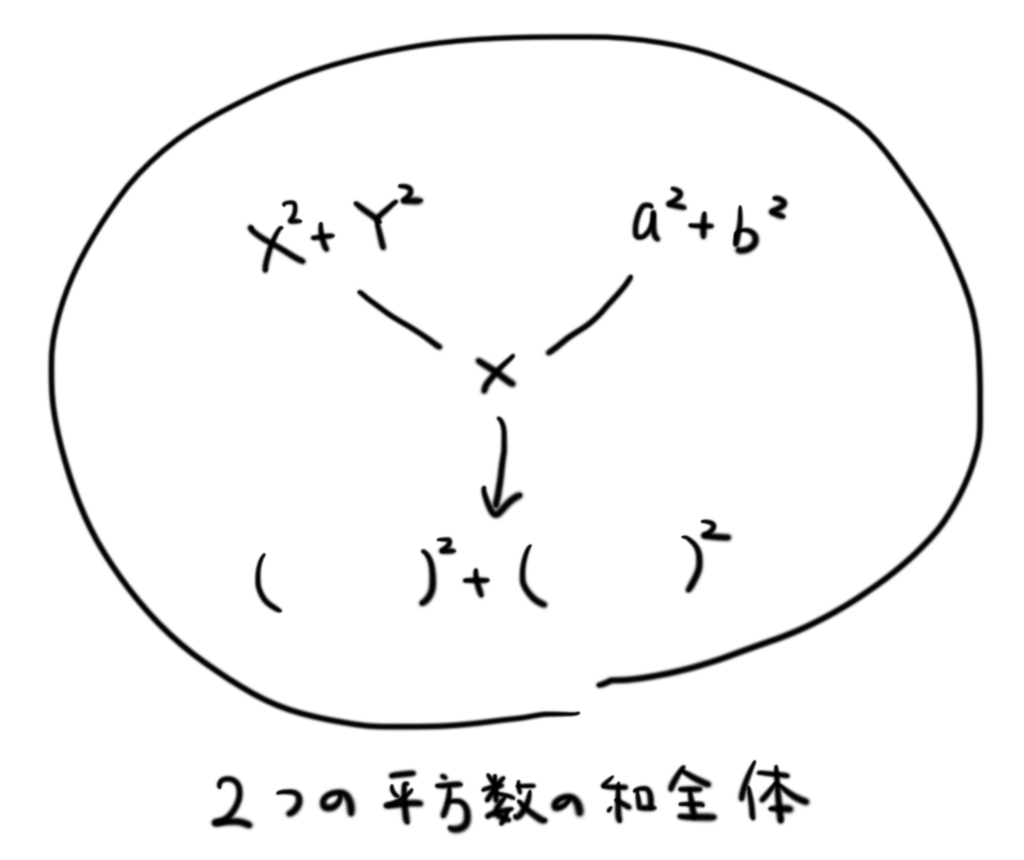
ブラーマグプタの恒等式は、私が一番好きな恒等式です。

ブラーマグプタの恒等式より

$\begin{align} 2^2 \times 5 &= (2^2 + 0^2)(2^2 + 1^2) \\ &= (2\cdot 2 + 0\cdot 1)^2 + (2\cdot 1 - 0 \cdot 2)^2 \\ &= 4^2 + 2^2 \end{align}$

が得られます。

一応検算しておくと、 $2^2\times 5 = 20$ ですが

$4^2 + 2^2 = 16 + 4 = 20$

はちゃんと成り立っていますね。

もう一度ブラーマグプタの恒等式より

$\begin{align} 2^2 \times 5 \times 101 &= (4^2 + 2^2)(10^2 + 1^2) \\ &= (4\cdot 10 + 2\cdot 1)^2 + (4\cdot 1 - 2 \cdot 10)^2 \\ &= 42^2 + (-16)^2 \end{align} \tag{11}$

となります。

結局、2020を表す「2つの平方数の和」が次の通り得られましたね！

$2020\; (= 2^2\times 5\times 101) = 42^2 + 16^2 \tag{12}$

もう一つの「2つの平方数の和」については、平方数の中身をうまくマイナスに置き換えることで求まります。

$2^2 \times 5 = 4^2 + 2^2$

でしたが、

$2^2 \times 5 = 4^2 + (-2)^2$

と置き換えても等式は成り立ちますね。

これを使ってあげれば、式 $(12)$ と同様に計算できます：

$\begin{align} 2^2 \times 5 \times 101 &= (4^2 + (-2)^2)(10^2 + 1^2) \\ &= (4\cdot 10 + (-2)\cdot 1)^2 + (4\cdot 1 - (-2) \cdot 10)^2 \\ &= 38^2 + 24^2 \end{align}$