不思議な法則 - tsujimotterのノートブック

ここに二つの2次無理数があります。

$\displaystyle \alpha_1 = \sqrt{-5}, \;\; \alpha_2 = \frac{1+\sqrt{-5}}{2}$

$\alpha_1, \alpha_2$ は、どちらも判別式が $D = -20$ となる2次無理数となっています。

$\alpha$ が2次無理数であるとは、 $\alpha$ が既約な2次方程式

$a\alpha^2 + b\alpha + c = 0$

の解であるということです。このとき、 $D(\alpha) = b^2 - 4ac$ を $\alpha$ の判別式と言います。判別式が負であるような2次無理数を虚2次無理数と言います。今回は虚2次無理数を扱います。

虚2次無理数 $\alpha$ を上半平面 $H$ で考えることにして、 $\alpha \in H$ には $\text{SL}_2(\mathbb{Z})$ の元による一次分数変換を考えることができます。

$\displaystyle \beta = \frac{a\alpha + b}{c\alpha + d}$

このとき、 $\beta$ も虚2次無理数となり、判別式も $D(\beta) = D(\alpha)$ となり保存されます。このように $\text{SL}_2(\mathbb{Z})$ による一次分数変換で移り合うとき、 $\beta$ と $\alpha$ は対等であるといいます。

なお、上の $\alpha_1, \alpha_2$ はどちらも対等ではないことに注意します。

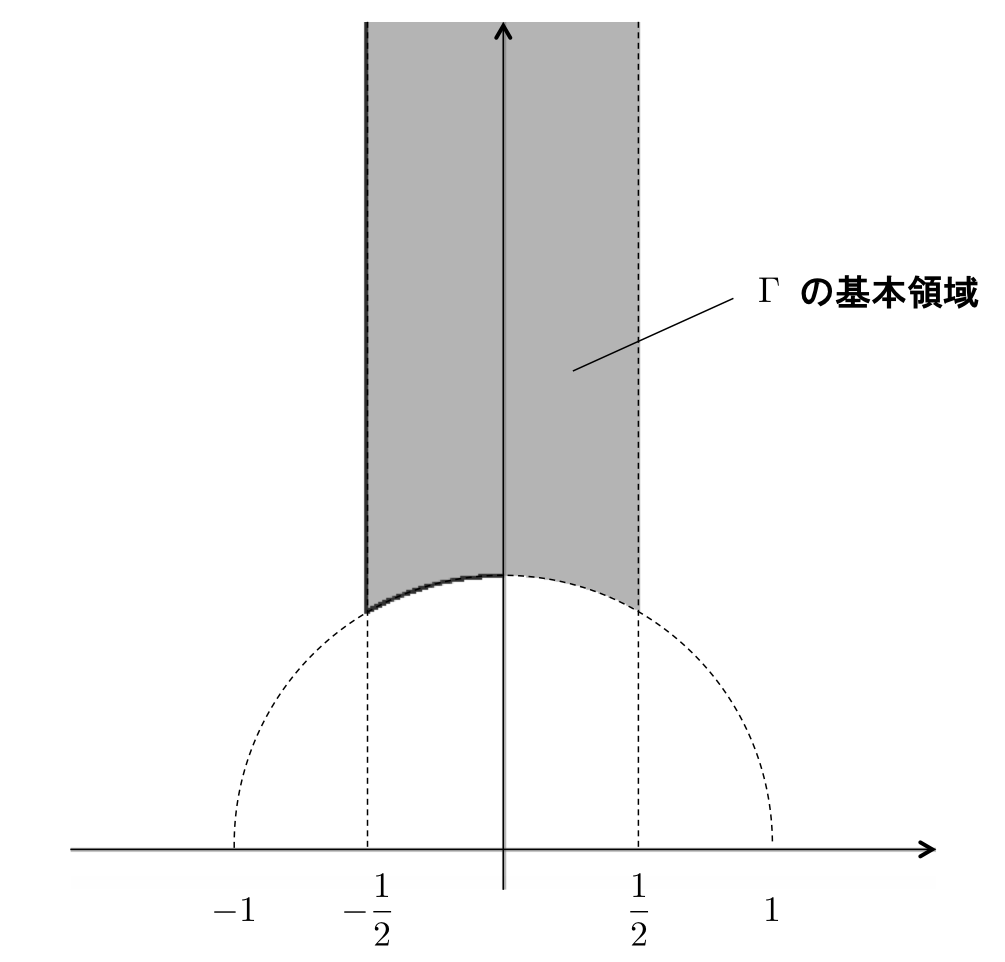
ちなみに、判別式 $D = -20$ である2次無理数かつ対等ではないものは、 $\text{SL}_2(\mathbb{Z})$ の基本領域（以下の図）の中には "2個" しか存在しません。この "2個" という数は、判別式が $D = -20$ である虚2次体の類数と一致しますが、これは偶然ではありません。

f:id:tsujimotter:20180603235652p:plain:w400

さて、 $\alpha_1, \alpha_2$ に対して、楕円モジュラー関数 $j(\tau)$ の値を計算します。楕円モジュラー関数は、以下の $q$ -展開によって計算できます。

$\begin{align} j(\tau) = &1/q \\ &+ 744 \\ &+ 196884q \\ &+ 21493760q^{2} \\ &+ 864299970q^{3} \\ &+ 20245856256q^{4} \\ &+ 333202640600q^{5} \\ &+ 4252023300096q^{6} \\ &+ 44656994071935q^{7} \\ &+ 401490886656000q^{8} \\ &+ 3176440229784420q^{9} \\ &+ 22567393309593600q^{10} \\ &+ \cdots \end{align}$

ここで、 $q = e^{2\pi i \tau}$ です。

計算すると、

$\begin{align} j(\alpha_1) &\approx 1264538.9094751414 \\ j(\alpha_2) &\approx -538.9094751405099 \end{align}$

となります。

ここで、両者の和と積をとると

$\begin{align} j(\alpha_1) + j(\alpha_2) &\approx 1264000.000000001 \\ j(\alpha_1) \, j(\alpha_2) &\approx -681472000.0000013 \end{align}$

実はこれらの値は整数値をとります。このことを知っていると

$\begin{align} j(\alpha_1) + j(\alpha_2) &= 1264000 \\ j(\alpha_1) \, j(\alpha_2) &= -681472000 \end{align}$

となることがわかり、和と積がわかっているので $j(\alpha_1), j(\alpha_2)$ を根に持つような整係数多項式を考えることができます。

$H_{-20}(X) := X^2 - 1264000X -681472000$

これを判別式 $D = -20$ の類多項式（class polynomial）といいます。つまり、虚2次無理数の最小多項式ということですね。

この方程式を解くことで、 $j(\alpha_1), j(\alpha_2)$ の値を次のように厳密に求めることができます。

$\begin{align} j(\alpha_1) &= 632000 + 282880\sqrt{5} \\ j(\alpha_2) &= 632000 - 282880\sqrt{5} \end{align}$

面白いですね。

ここからが本題です

2次形式 $X^2 + 5Y^2$ で表せる素数の法則について考えます。

このお話は、これまでもtsujimotterのノートブックで扱ってきました。

参考：
tsujimotter.hatenablog.com
tsujimotter.hatenablog.com

上の２つの記事で与えたように、例外的な有限個の素数（ $p = 2, 5$ ）を除けば

$p = X^2 + 5Y^2 \;\; \Longleftrightarrow \;\; p \equiv 1, 9 \pmod{20}$

という法則が成立するのでした。

しかし、この法則を与えるのはそう簡単ではありません。いつものように平方剰余による条件

$\displaystyle \left(\frac{-5}{p}\right) = 1 \tag{1}$

を考えると、これは条件 $p \equiv 1, 3, 7, 9 \pmod{20}$ を与えますが、この条件は $X^2 + 5Y^2$ で表せる素数の必要条件しか与えません。十分条件を与えるためには、より深い考察が必要です。

ここで、上記 $(1)$ に加えて、判別式 $D = -20$ の類多項式 $H_{-20}(X)$ を用いた以下の条件を考えましょう。

$H_{-20}(X) \equiv 0 \pmod{p} \; \text{が解を持つ} \tag{2}$

なんと、驚くべきことに、 $(1)$ かつ $(2)$ という条件が $p = X^2 + 5Y^2$ とかけるための必要十分条件となっています。

実験してみましょう。 $p \neq 2, 5, \; p < 100$ で考えます。

$p$	$\left(\frac{-5}{p}\right)$	$H_{-20}(X) \equiv 0 \pmod{p}$	$p = X^2 + 5Y^2$
$3$	$-1$	解を持つ	－
$7$	$-1$	解を持つ	－
$11$	$+1$	解を持たない	ー
$13$	$+1$	解を持たない	ー
$17$	$+1$	解を持たない	ー
$19$	$+1$	解を持たない	ー
$23$	$-1$	解を持つ	ー
$29$	$+1$	解を持つ	$29 = 3^2 + 5\cdot 2^2$
$31$	$+1$	解を持たない	ー
$37$	$-1$	解を持たない	ー
$41$	$+1$	解を持つ	$41 = 6^2 + 5\cdot 1^2$
$43$	$-1$	解を持つ	ー
$47$	$-1$	解を持つ	ー
$53$	$-1$	解を持たない	ー
$59$	$+1$	解を持たない	ー
$61$	$+1$	解を持つ	$61 = 4^2 + 5\cdot 3^2$
$67$	$-1$	解を持つ	ー
$71$	$+1$	解を持たない	ー
$73$	$-1$	解を持たない	ー
$79$	$+1$	解を持たない	ー
$83$	$-1$	解を持つ	ー
$89$	$+1$	解を持つ	$89 = 3^2 + 5\cdot 4^2$
$97$	$-1$	解を持たない	ー