6xx + xy + yy の形で表せる素数

昨日の記事の続きで「二平方定理」について調べている中で，興味深い定理を発見しました。

今日は

「どんな形をした素数が， $p = 6x^2+xy+y^2$ の形に書けるか」

についてのお話をご紹介します。

前回までのおさらいと今回の目標

簡単におさらいすると，昨日の記事では，

「 $6n+1$ 型の素数は $p = x^2+3y^2$ の形で表せる」

ことを示し，その前の記事では，

「 $4n+1$ 型の素数は $p = x^2+y^2$ の形で表せる」

ことを示しました。

一般に，

$ax^2 + bxy + cy^2$

の形で表される式のことを「二次形式」といいます。これまでの２つの記事では「特殊な二次形式」で表される素数 $p$ の特徴について考えていたのでした。

この二次形式について， $a = 6, b = 1, c = 1$ のとき，つまり

$p = 6x^2 + xy + y^2$

では，果たしてどうなるでしょうか，というのが今日のテーマです。

ちなみに，この形で表される素数 $p$ は， $1000$ 以下では次の $26$ 個です。

$23, 59, 101, 167, 173, 211, 223, 271, 307, 317,$

$347, 449, 463, 593, 599, 607, 691, 719, 809, 821,$

$829, 853, 877, 883, 991, 997$

最初の方だけ確認してみると，

$23 = 6\cdot 2^2 + 2\cdot (-1) + (-1)^2$

$59 = 6\cdot 2^2 + 2\cdot (-7) + (-7)^2$

$101 = 6\cdot 4^2 + 4\cdot (-5) + (-5)^2$

となって，たしかに $6x^2 + xy + y^2$ の形で表せていることがわかります。

（昨日までの話と）同様に考えるのであれば，この素数 $p$ が $an + b$ の形で書けるかどうか，考えたくなりますね。しかしこれらの素数は，このような形で表すことが出来ないことが知られているそうです。

かといって，まったく法則がないかといえば，そうではありません。

その法則が実に面白いのです！！

保型形式と二次体

まず唐突に，保型形式と呼ばれる特徴を持つ，次の式を考えます。

$\displaystyle f = q\prod_{n=1}^{\infty} (1-q^n)(1-q^{23n}) = \sum_{n=1}^{\infty} a_n q^n$

ここで $a_n$ は，左辺の積を展開したときに現れる $q^n$ の係数として定義されます。この $a_n$ をフーリエ係数と呼びます。

このフーリエ係数を使うと，先ほどの素数の持つ特徴を，驚くほどきれいな法則として表すことが出来ます。

さぁ，その法則をご覧に入れましょう。

定理：
$23$ を除く素数 $p$ に対して，
$a_p = 2 \Longleftrightarrow p = 6x^2 + xy + y^2$

なんということでしょう！！！
（驚いてください。笑）

なぜそんなことが起きるのか。「保型形式のフーリエ係数」と「二次形式」がいったいどうして関係があるのか，tsujimotter には検討もつきません。

参考文献によると，虚二次体 $\mathbb{Q}(\sqrt{-23})$ の整数環 $\mathbb{Z}\left[ \frac{1+\sqrt{-23}}{2}\right]$ においては，上記にあげた素数 $p$ が

$\displaystyle \left(x\frac{1+\sqrt{-23}}{2} + y \right) \left(x\frac{1-\sqrt{-23}}{2} + y \right)$

のように分解する，というのがキーのようです。

これを展開すると，

$\displaystyle \left(x\frac{1+\sqrt{-23}}{2} + y \right) \left(x\frac{1-\sqrt{-23}}{2} + y \right) = 6x^2 + xy + y^2$

となって，目的の式が得られます。

問題は「二次体が与えられたときに，どのような $p$ が分解されるのか」という点ですが，これがまさに「類体論」と呼ばれる数学に深く関わってくるのだそうです。

面白そうな匂いがぷんぷんしますね！！

数式処理システムで確認する

とりあえず，上の定理が本当に成立しているかどうか，確認してみたいと思いました。

そのためには， $f$ の式の展開が必要ですが，これがなかなか厄介です。展開するだけで大変なのに，最初に $a_p = 2$ となるのが $p = 59$ のときなので，少なくとも $59$ 回は積をとる必要があります。

というわけで，式の展開を自動化したいのですが，自分でプログラムを作るのも面倒です。

そこで，数式処理システムを使いましょう！ Maxima の出番です！

実は，Maxima を使うのは，今回がはじめてです。
このためだけにインストールしました！

以前より，以下のブログを見ていつかは触ってみたいなと思っていました。まさかここまで実用的な理由が出来るとは思いませんでしたが。笑

Maxima で綴る数学の旅

この Maxima を使うと，数式の展開が簡単に行えます。

たとえば，

$(1-q^n)(1-q^{23n})$

を計算したいときは，

(%i1) expand( ((1-q^n)*(1-q^(23*n))) );

のように打ち込むと，

                             24 n    23 n    n
(%o1)                       q     - q     - q  + 1

と帰ってきます。

TeX 形式にすることも出来て，

(%i2) tex(%);
$$q^{24\,n}-q^{23\,n}-q^{n}+1$$
(%o2)                                false

と帰ってきます。これをブログに貼付けると，

$q^{24\,n}-q^{23\,n}-q^{n}+1$

となります。ちゃんと展開できていますね。ってか便利ですね！！

ちなみに，"%" は直前に評価した結果を意味する記号です。

さて，本題の式を計算しましょう。

$\displaystyle q\prod_{n=1}^{\infty} (1-q^n)(1-q^{23n})$

見るからにややこしいですね。

以下のように，

$\displaystyle q\prod_{k=1}^{n} (1-q^k)(1-q^{23k})$

として， $n = 100$ まで計算しましょう。

まず，多項式を「昇べき順」に並べるように設定します。

powerdisp:true$

次に， $\prod$ の中身を $a_n$ と定義します。

a[n]:=((1-q^n)*(1-q^(23*n)));

では，式を展開しましょう。まずは，ちょっと怖いので $n = 10$ で。

tex( expand( q*product( a[k], k, 1, 10 ) ) );

計算結果はこうなります。

$q-q^2-q^3+q^6+q^8+\cdots$

本当は，この先も項は続くのですが， $n = 10$ までしか計算していないので，正しいのはここまでです。

それで，ですね。
このまま一気に $100$ までいきたいところなんですが・・・。

結論から述べると無理です。

どうやら， $n$ を増やしていくと，爆発的に項の数が増えていくのですね。すると，それに伴って，展開にかかる時間も増えていくわけです。

tsujimotter の非力な Mac Book Air で試したところ， $n = 20$ が限界でした。

tex( expand( q*product( a[k], k, 1, 20 ) ) );

残念ながら，得られたのはここまででした。

$q-q^2-q^3+q^6+q^8-q^{13}-q^{16}+\cdots$

$n = 23$ にすら到達しない・・・。

結局・・・

というわけで，仕方ないので参考文献からコピーしてきます。

以下のようになるそうです。

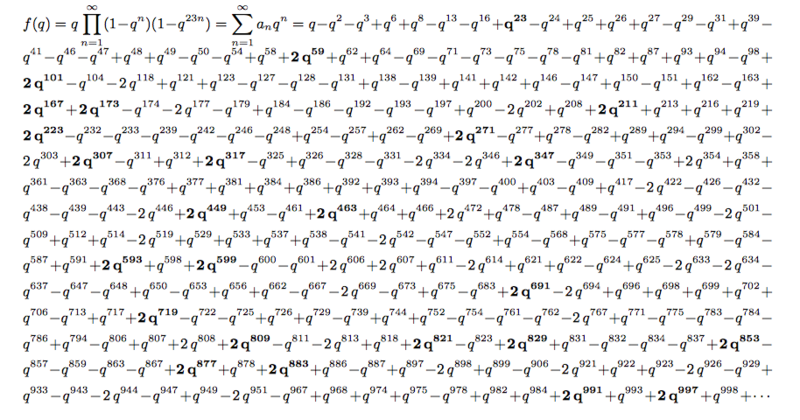
注目してほしいのは太字部分です。この太字は， $p = 6x^2 + xy + y^2$ となる素数に対応した項を表しています。

$p = 23$ を除くと，すべての $p$ で $a_p = 2$ となっていますね。逆に，その他の $n$ に対しては，すべて $a_n \neq 2$ となっていることもわかります。

たしかに，上の定理は成り立っていました！

おわりに

いやー，実に興味をそそられるテーマでしたね！

この話の根底には「非可換類体論」と呼ばれる数学が関係しているそうです。今の tsujimotter には，まったく意味が分かりませんが，いつかはきっと理解したいなと強く思いました！

参考文献

以下の文献を発見して tsujimotter は本当に興奮しました。その思いをこの記事にぶつけてみました。

内容はこちらの文献に，完全に依存しています。間違いがあるとすれば，きっと私の理解不足です。。。

伊藤哲史「平方数の和で表される素数について」城咲新人セミナー
~~https://www.math.kyoto-u.ac.jp/insei/proceeding/2010/ito.pdf~~
https://drive.google.com/file/d/1RrC0WG676Hv3k2W0pfK6LY00hiC0kaR0/view
（リンク先が変わりました）