位数6の群の分類 - tsujimotterのノートブック

私がスタッフとして携わっている日曜数学会というイベントが、今月の20日に 6周年を迎えます。めでたいですね。また、先日私の年齢も $36$ 歳になりまして、つまり $36 = 6^2$ というわけですね。ダブルでめでたい（？）。

せっかくなので、何か $36$ にまつわる発表をしたいなと思いました。私は最近「表現者のための数学」という講座をやっていまして、その講座のテーマが群論です。準備のために群論の勉強をしているところです。

そこで、位数 $36$ の群の分類をやろうと思い立ったのです。

しかし・・・

f:id:tsujimotter:20210614233324p:plain:w400

そう、挫折したのです。

群の分類というのは思った以上に難しいもので、位数の約数が増えれば増えるほど難しくなります。なんとかなるだろうと思ったのですがダメでした。

私が位数36に挑戦するのは少し早かったようです。

そこで、練習台としてもう少し簡単な位数から始めようと思いました。それが表題の位数 $6$ の群の分類です。

群の分類の面白さ

「群の分類は難しい」と書いたのですが、一方で面白いものだと思っています。

群とは以下の４つの公理を満たす集合（と演算の組）のことです。

定義（群）

集合 $G$ とその上で定義される演算 $\times$ が以下の４つの公理を満たすとき、 $(G, \times)$ は群であるという：

（演算が閉じている） 任意の $a, b \in G$ に対し $a\times b \in G$ である。
（結合則） 任意の $a, b, c \in G$ に対し、 $a\times(b\times c) = (a\times b)\times c$ が成り立つ。
（単位元の存在） ある $e \in G$ が存在し、任意の $a \in G$ に対し、 $a\times e = e\times a = a$ が成り立つ。
（逆元の存在） 任意の $a \in G$ に対し、ある $a^{-1} \in G$ が存在し、 $a\times a^{-1} = a^{-1}\times a = e$ が成り立つ。

このように群というのはたった４つしか公理がないにも関わらず、位数（要素数のこと）が指定されるとたちまち取りうる群の構造が決まってしまうのです。

また、群の構造を絞り込んでいく過程も面白いなと思っています。群論のあらゆる道具を使ってじわじわ追い詰めていく感じなのですが、これが推理小説で犯人を追い詰めていくのと似ていて面白いなと思います。（個人の感想です。）

そんなわけで、今回は群論を使って構造を特定していく過程の面白さを紹介できればと思っています。

このような証明を紹介するときには、無機質に証明していく感じになりがちだと思いますが、今回は少し工夫しています。

まず、一つ目の工夫として「どのような方向で証明していくのか」を表すフローチャートを作ります。これがあることで、全体像やどこまで証明できたのかが見えやすくなります。

もう一つの工夫として「現在我々がどこまでの情報を得ているのか」を示す図を使います。具体的には、こんな図を使います：

f:id:tsujimotter:20210614233414p:plain:w360

これは今考えている位数 $6$ の群 $G$ を表しています。現在は要素数が $6$ であることだけが分かっているので、 $6$ つの要素を★印で表しています。☆はただ一つ存在する元である単位元のイメージです。

この状態ではほとんど何も分かっていないわけですが、証明が進んでいくうちにこんな図に変わっていきます。

f:id:tsujimotter:20210614235642p:plain:w380

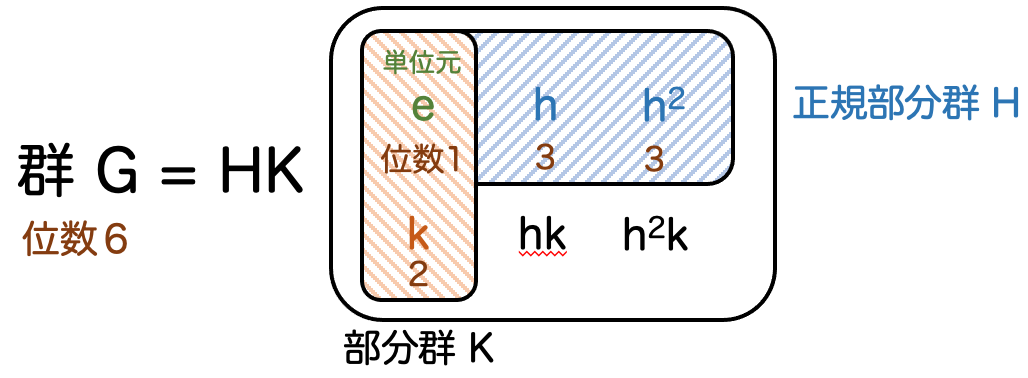
単なる★の集まりだったものが、名前がついたり、位数などの情報がついたりするわけです。

他人が書いた証明を見るときは、現在どこまで議論が進んでいるのかしばしば見失って付いていけなくなります。こういう情報があることで、読者が証明についていきやすくなることを狙っています。

必要な道具と前提知識

今回は、以下のような事実を使うことになります。

群・可換群の定義
部分群・正規部分群・群の位数・元の位数・準同型・同型 etc. 諸々の定義
ラグランジュの定理（あとで主張だけ紹介します）
群作用と置換表現

使わないものとしては、シローの定理があります。これは群の分類をする上で大変便利な代物なのですが、今回の場合使ってしまうとかなり問題が楽になってしまうのであえて使わない方向で行こうと思います。
（証明もそれなりに大変ですし。）

群論の本当に色々な道具を使うので、群論そのものの勉強にもなります。群論の定理で、「こんなのいったい何に使うのだろう」と思っていたものが、群の分類では悉く必要になるのです。

こうした道具を勉強するモチベーションにもなるかなと思うので、その意味でも群の分類はよい演習問題になるかと思います。

なので、色々知らない道具とかも出てくると思いますが、それについては何となく流し読みした上で、興味を持った方は教科書で勉強いただけると嬉しいです。

さて、前置きが長くなりましたが、本題の分類に行きましょう。

位数 $6$ の群の分類

まず、最初の時点では $G$ の状態は次のようになっています。

つまり、位数 $6$ ということ、単位元が唯一存在することだけが分かっています。

議論の出発点になるのは、ラグランジュの定理です。

定理（ラグランジュ）

$G$ を有限群、 $H$ をその部分群とする。このとき、次が成り立つ：

$\# G = \#H \cdot (G : H)$

ただし、 $\#G, \#H$ は $G, H$ の位数、 $(G : H)$ は $H$ で割った剰余類の個数。

「剰余類」という言葉が出ていますが、ここではそこまで難しいことは使いません。使うのは、部分群の位数は必ず元の群の約数になるということです。これはかなり大きな制約となります。

また、 $G$ から何か一つ元 $g$ をとってきたときに、その元が生成する $G$ の部分群を $\langle g\rangle$ とします。これは巡回群になります。すると、この部分群もラグランジュの定理の制約を受けますので、 $\langle g\rangle$ の位数は $\#G$ の約数となります。 $\langle g\rangle$ の位数は $g$ の位数（ $g^n =e$ となる最小の正の整数 $n$ ）に一致します。

したがって、次の事実が言えるわけです：

$G$ の任意の元 $g$ の位数は、 $1, 2, 3, 6$ のいずれかである。

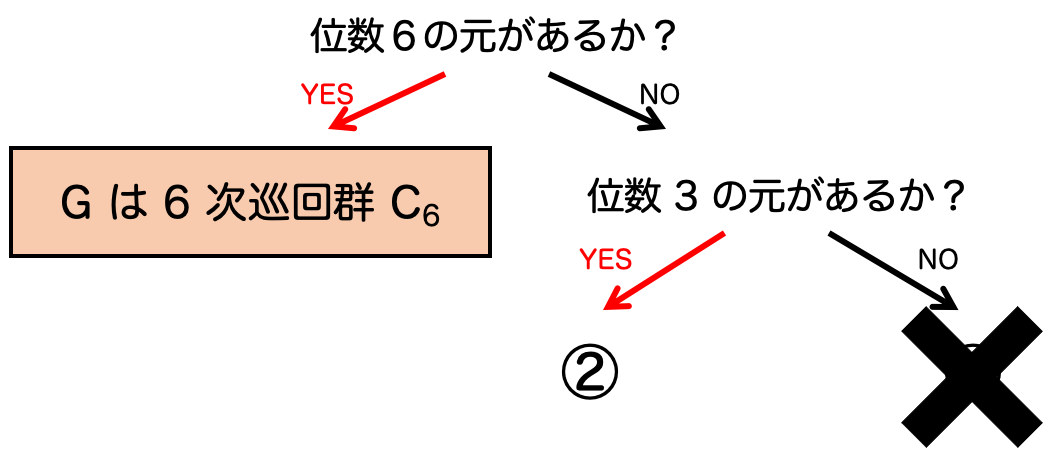
そこで、位数 $n$ の元があるかどうか、という点で群を分類するフローチャートが得られるわけです。

f:id:tsujimotter:20210614233455p:plain:w360

「位数 $6$ の元はあるか？」という質問に対し「YES」であれば、任意の元はその位数 $6$ の元で生成されることになります。したがって、この場合位数 $6$ の巡回群 $C_6$ に同型ということになります。
（任意の位数 $n$ の巡回群 $G$ から、 $C_n$ への生成元を生成元に移す同型写像が得られますので、同型です。）

したがって、以下は位数 $6$ の元が存在しない場合を考えればよいことになります。

そこで、位数 $3$ の元がない場合（①）と、位数 $3$ の元がある場合（②）に分けて議論を進めていきましょう。

① 位数 $6$ の元がなく、位数 $3$ の元もない場合

ラグランジュの定理より元の位数は $1, 2, 3, 6$ のいずれかに限られます。位数 $6$ の元も位数 $3$ の元もない状況では、位数 $2$ または位数 $1$ しかありえません。

位数 $1$ ならば単位元であり、単位元はただ一つしかありませんので、残りはすべて位数 $2$ の元となります。

f:id:tsujimotter:20210614233520p:plain:w360

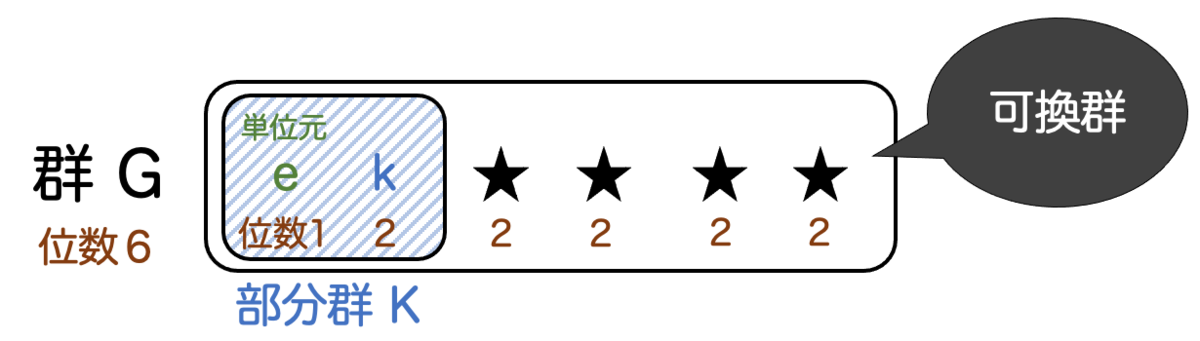
さて、位数 $2$ 以下の元しかないことを使って、次を示したいと思います。

$G$ の元は位数 $2$ 以下 $\;\; \Longrightarrow \;\;$ $G$ は可換群。

（∵） $a, b \in G$ を任意にとると、位数 $2$ 以下なので $a^2 = b^2 = e$ 。 $a^{-1} = a, \; b^{-1} = b$ である。

よって

$ab(ba)^{-1} = aba^{-1}b^{-1} = abab = (ab)^2$

であり、 $ab \in G$ は位数 $2$ 以下なので $(ab)^2 = e$ である。

したがって、 $ab = ba$ であり、 $G$ が可換群であることが示された。□

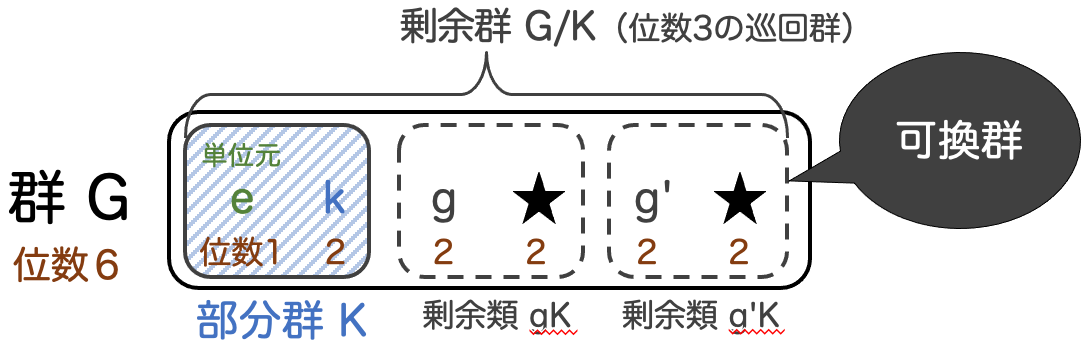
可換群であることから次を示します。

$G$ は可換群 $\;\; \Longrightarrow \;\;$ 位数 $3$ の元がある（矛盾）。

（∵） 位数 $2$ の元を一つとって $k \in G$ とする。このとき、 $k$ が生成する $G$ の部分群を $K = \langle k \rangle$ とすると、これは位数 $2$ の部分群となる。

f:id:tsujimotter:20210614233630p:plain:w380

ここで $G$ は可換群より、任意の部分群は正規部分群であるから、 $K$ は正規部分群。したがって、 $G/K$ は群であり、ラグランジュの定理より位数 $3$ の巡回群となる。

f:id:tsujimotter:20210614234826p:plain:w380

$G$ から $K$ を除いた差集合（これを $G\setminus K$ と書く）から一つ元 $g \in G\setminus K$ をとる。 $G/K$ が位数 $3$ の巡回群であることから、 $G/K$ の元は $3$ 乗すると $G/K$ の単位元に移る。つまり、 $g^3 \in K$ である。すなわち、 $g^3 = e$ または $g^3 = k$ である。

$g^3 = k$ のとき、 $g$ は位数 $2$ でもあることから $g^2 = e$ であり、よって $g = k$ である。しかしこれは $g \in G\setminus K$ であることに反する。

よって、 $g^3 = e$ であることになるが、これは位数 $3$ の元があることに反する。したがって、矛盾が導かれ、①の条件は成立しないことがわかる。□

f:id:tsujimotter:20210614234912p:plain:w360

② 位数 $6$ の元がなく、位数 $3$ の元がある場合

最後に、位数 $3$ の元がある場合について考えます。

位数 $3$ の元を $h$ とし、 $h$ が生成する $G$ の部分群を

$H = \langle h\rangle = \{ e, h, h^2 \}$

とします。これは位数 $3$ の巡回群です。

f:id:tsujimotter:20210614235057p:plain:w360

ここで次を示します。

$H$ は $G$ の正規部分群。

（∵） $g \in G\setminus H$ をとり、 $H$ による左剰余類 $H, gH$ を考える。これは共通部分を持たないので

$G = H \cup gH$ かつ $H \cap gH = \emptyset$

である。また、右剰余類を考えると

$G = H \cup Hg$ かつ $H \cap Hg = \emptyset$

である。よって $gH = Hg$ が言える。これは $H$ が正規部分群であることを意味する。□

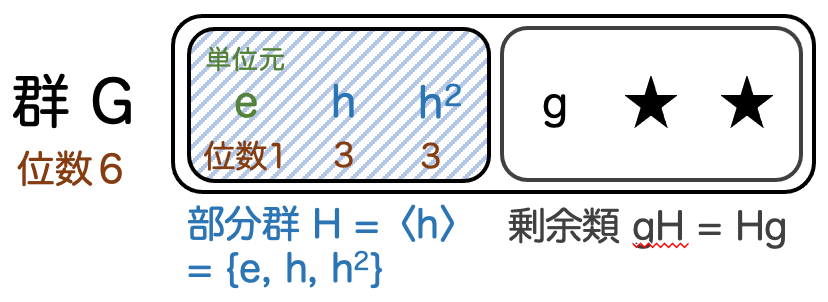
f:id:tsujimotter:20210614235343p:plain:w360

ここで、 $G\setminus H$ から一つ元 $k$ をとって固定します。また、 $k$ が生成する $G$ の部分群を $K = \langle k\rangle$ とします。

f:id:tsujimotter:20210614235427p:plain:w360

まだ、 $k$ の位数はわからないので、次を示します：

$k$ は位数 $2$ 。

（∵） 位数 $6$ の元は存在しないので、 $k$ の取りうる位数は $2$ か $3$ のいずれかである。

位数 $3$ であれば $k^2 \neq e$ である。 $G/H$ はラグランジュの定理より位数 $2$ なので、 $k^2 \in H$ である。よって

$k^2 = h$ または $k^2 = h^2$ である。

どちらも $k$ を左からかけると $k^3 = kh$ または $k^3 = kh^2$ となり $k^3 = e$ であることから $kh = e$ または $kh^2 = e$ である。これは $k$ が $h$ または $h^2$ の逆元であることを意味するが、 $k \in G\setminus H$ であることに矛盾する。

したがって、 $k$ の位数は $2$ であることがわかる。
（ちなみに、 $k$ は今固定した１つの元を考えているが、 $k$ の取り方は任意なので、 $G\setminus H$ の任意の元は位数 $2$ であることがわかる。）□

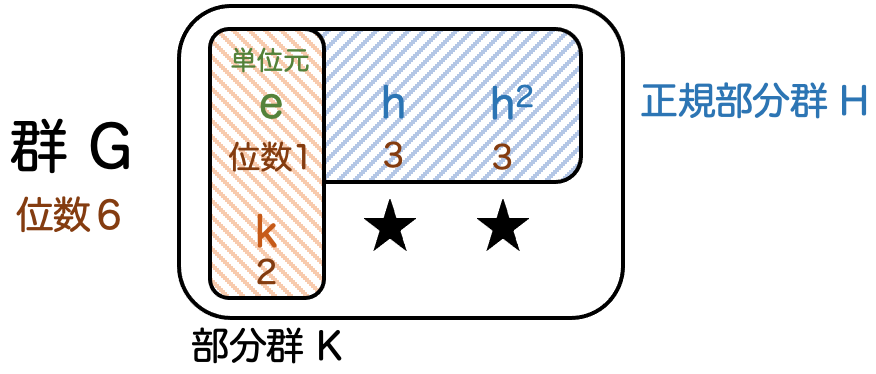
f:id:tsujimotter:20210614235538p:plain:w360

ここで、 $h^i k^j$ （ $i = 0, 1, 2, \; j = 0, 1$ ）の形の元全体を $HK$ とします。これは $G$ の部分集合ではありますが、部分群であるとは限りません。ところが $H$ は正規部分群なので、 $k^j H = H k^j$ です。よって

$(h^{i_1} k^{j_1})(h^{i_2} k^{j_2}) = (h^{i_1} h^{i_3}) (k^{i_1} h^{i_2}) \in HK$

となることがわかります。（演算が閉じている）

また

$(h^{i} k^{j})^{-1} = k^{-j} h^{-i} = h^{i'} k^{-j} \in HK$

より、逆元があることもわかります。

したがって、 $HK \subset G$ は部分群です。

また、 $\{e, h, h^2, k\} \subset HK$ より、 $HK$ の位数は $4$ 以上です。

$G$ の部分群は $6$ の約数なので、 $\#HK = 6$ であることが分かります。よって、 $HK = G$ であることが結論付けられます。

したがって、 $G$ の任意の元は $h^i k^j$ の形で表せることが分かりました。

f:id:tsujimotter:20210614235642p:plain:w360

また、 $H$ は正規部分群より、 $khk^{-1} \in H$ です。したがって

(i) $khk^{-1} = e$

(ii) $khk^{-1} = h$

(iii) $khk^{-1} = h^2$

のいずれかとなります。

(i) だと $kh = k$ であり、左から $k^{-1}$ を書けると $h = e$ となり矛盾します。

したがって、(ii) または (iii) のケースだけ考えればよいことになります。

(ii) $khk^{-1} = h$ のとき、 $G = C_6$ （「位数 $6$ の元はない」に矛盾）

（∵） $kh = hk$ より、 $G$ は可換群である。よって、 $K$ も正規部分群である。

$H, K$ は正規部分群であり、 $H \cap K = \{e\}$ である。このとき、 $H\times K$ から $G$ への写像

$\begin{align} \phi \colon H\times K\;\; &\longrightarrow \;\; G, \\ (h^i, k^j) \;\; &\longmapsto \;\; h^i k^j \end{align}$

を考える。これは明らかに全射であり、 $h^i k^j = e$ のとき、 $h^i = k^{-j} = k^j$ であり、 $H\cap K = {e}$ より $i = j = 0$ 。すなわち、 $\phi$ は単射である。

また、 $h$ と $k$ の可換性より準同型写像でもある。したがって、 $\phi$ は同型写像。

よって $G \simeq H\times K$ であることがわかった。ここで、 $H = C_3$ 、 $K = C_2$ であるので、中国剰余定理より

$G \simeq H\times K \simeq C_3 \times C_2 \simeq C_6$

である。すなわち $G \simeq C_6$ であることがわかった。

しかしながら、 $G$ は位数 $6$ の元を持たないので、これは矛盾。□

(iii) $khk^{-1} = h^2$ のとき、 $kh = h^2 k$

（∵） $kh = h^2 k$ はただちにわかる。□

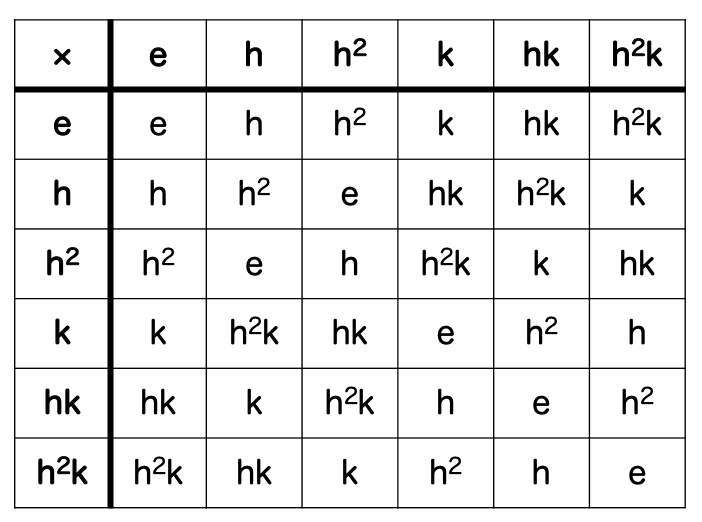
この性質

$kh = h^2 k$

があることによって、 $G$ の任意の元の積が完全に決定できます。

たとえば $hk, h^2k$ の積は

$(hk) (h^2 k) = h(kh)hk = hh^2(kh)k = h^3 h^2 k k = h^2$

となります。

これをすべての元同士で実行すれば、 $G$ の乗法表（群表）が得られるわけです。

実際実行すると、（少し大変ですが）こうなります：

f:id:tsujimotter:20210614235746p:plain:w330

これで終わりにしてもいいわけですが・・・

この群 is 何？

って感じですよね。

②-(iii) の群は何なのか？

これまで分かったことをフローチャートにまとめると次のようになります。

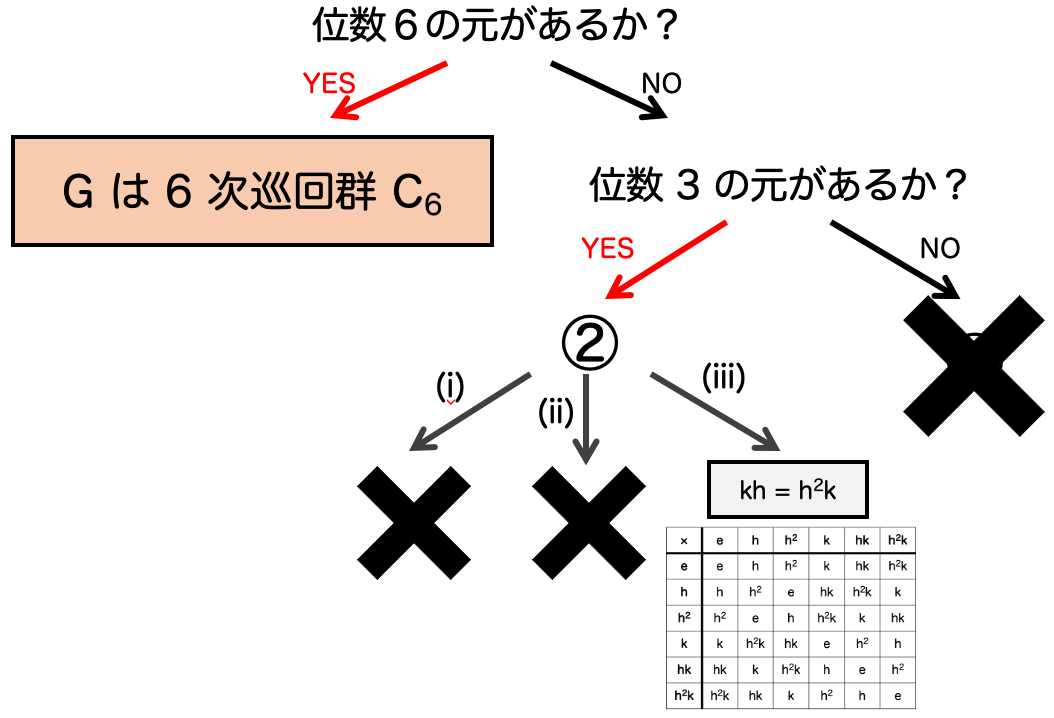
f:id:tsujimotter:20210615000357p:plain:w380

ここで「②-(iii)の群がいったいどのような群なのか」という問題だけが残っています。それを考えるキーになるのが置換表現です。

群 $G$ の中で、 $H = \{e, h, h^2\}$ に属さない元

$X = \{ k_1 = k, \; k_2 = hk, \; k_3 = h^2k \}$

について考えましょう。

これらは先ほど議論したようにすべて位数 $2$ の元となります。

実は、これらは互いに共役の関係にあります。 $g$ と $g'$ が共役であるとは、ある元 $h$ が存在して $g' = hgh^{-1}$ と書けることを言います。

実際

$hk_1 h^{-1} = hkh^2 = h^2k = k_3$
$h^2k_1 h^{-2} = h^2kh = h^4k = hk = k_2$

が成り立ちます。

したがって、 $G$ の元は $X$ の元に対して共役によって作用することが分かります。ここから、 $g \in G$ に対して

$x \longmapsto g x g^{-1} \;\;\;\; (x \in X)$

なる写像が定まります。これは有限集合 $X$ に対する全単射となります。

$X$ は3元集合なので、

$k_1, k_2, k_3$

の置換ということになるわけですね。

よって、 $S_3$ を $3$ 次の置換全体のなす群（ $3$ 次対称群）とすると

$\rho\colon G \longrightarrow S_3$

なる写像が定まります。ここで $\rho$ は $g k_{i} g^{-1} = k_{\rho(g)(i)}$ によって定めます。

さらに言えば、この $\rho$ は群準同型でもあります。それは以下のように分かります。

$(gh) k_i (gh)^{-1} = k_{\rho(gh)(i)}$
$(gh) k_i (gh)^{-1} = g (h k_i h^{-1}) g^{-1} = g(k_{\rho(h)(i)})g^{-1} = k_{\rho(g)\circ\rho(h)(i)}$

したがって

$\rho(gh) = \rho(g)\circ \rho(h)$

というわけですね。

このようにして得られる群準同型 $\rho\colon G \longrightarrow S_3$ のことを置換表現といいます。
（より一般に有限集合への群作用から置換表現が得られます。）

あとは、この準同型の行き先を具体的にすべて計算してみましょう。

$g = e$ のとき： $gk_1g^{-1} = k_1, gk_2g^{-1} = k_2, gk_3g^{-1} = k_3$ より

$\rho(e) = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}$

$g = h$ のとき： $gk_1g^{-1} = k_3, gk_2g^{-1} = k_1, gk_3g^{-1} = k_2$ より

$\rho(h) = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix}$

$g = h^2$ のとき： $gk_1g^{-1} = k_2, gk_2g^{-1} = k_3, gk_3g^{-1} = k_1$ より

$\rho(h^2) = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}$

$g = k$ のとき： $gk_1g^{-1} = k_1, gk_2g^{-1} = k_3, gk_3g^{-1} = k_2$ より

$\rho(k) = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix}$

$g = hk$ のとき： $gk_1g^{-1} = k_3, gk_2g^{-1} = k_2, gk_3g^{-1} = k_1$ より

$\rho(hk) = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix}$

$g = h^2 k$ のとき： $gk_1g^{-1} = k_2, gk_2g^{-1} = k_1, gk_3g^{-1} = k_3$ より

$\rho(h^2 k) = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix}$

したがって、実は $\rho$ が全単射であったことが分かるわけです。

群準同型かつ全単射なので、 $\rho$ は同型写像です。したがって、 $G \simeq S_3$ であることがわかりました。

すなわち、②-(iii) の $G$ は3次対称群 $S_3$ に同型であったというわけです。

これにて位数 $6$ の群の分類が完了しました。

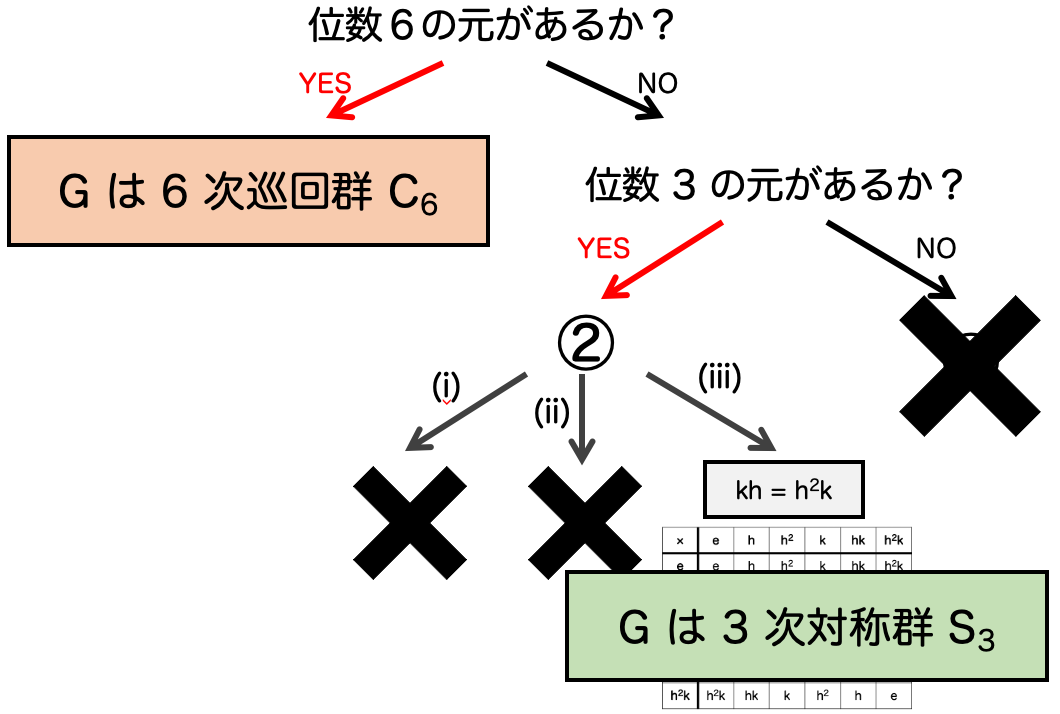
f:id:tsujimotter:20210615000557p:plain:w380

結論としては、以下のようになります：

位数 $6$ の群は、 $6$ 次巡回群 $C_6$ か $3$ 次対称群 $S_3$ のいずれかに同型である

おわりに

ラグランジュの定理によって元の位数におおざっぱなあたりをつけ、位数 $3$ の元が正規部分群であることを示し、その性質を使って大きく群を二つのタイプに分けたというわけでした。可換になる方が $6$ 次巡回群 $C_6$ であり、非可換な方が3次対称群 $S_3$ であるということでした。

まとめるとこうなりますが、結構いろんな性質を使いましたよね。あの手この手で、徐々に群を追い詰めて、これしか存在しない（真実はいつも一つ）というところまで持って行ったという感じでした。この辺が推理小説っぽくて面白いなと感じます。

また、本当に群論の性質だけを使って追い詰めることができるというのが面白いですね。

個人的には、 $S_3$ が対称群であることを示すのに、位数 $2$ の $3$ つの元に対する共役作用を考えるというのも面白いなと感じました。実際、このような考え方は、今回は使わなかったシローの定理でも出てくる考え方です。

$\# G = 6 = 2\cdot 3$ より、シローの定理によれば、 $2$ -シロー部分群と $3$ -シロー部分群が存在します。つまり位数 $3$ の部分群と位数 $2$ の部分群が存在するというわけです。あれだけ苦労した部分が一発で示せるのは強いですね。

位数 $3$ の方は共役が $1$ つであり、正規部分群となります。位数 $2$ の方は、互いに共役な $3$ つの部分群があります。これが $\langle k \rangle, \; \langle hk \rangle, \; \langle h^2 k \rangle$ というわけです。これらの間の共役作用を考えると群構造のヒントが得られる、というのが今回使った方法だったというわけです。