最近、寺杣先生の「リーマン面の理論」という本を勉強しています。
「リーマン面」についての勉強を始めたのは、「幾何が専門の人の話についていけるようになりたい」という動機からでした。そんなことを考えているときに上記の本が発売されたので、ちょうどよいタイミングだなと思いました。また、それとは別に「リーマン面」と「数論的な現象」の間に接点があるそうで、これについても理解したいなという思いがあります。
一方、tsujimotterはこれまで位相空間論や多様体の勉強をほとんどしてこなかったので、理解するのにだいぶ苦労しています。進捗は遅そうですが、少しずつでも読み進めようと思っています。
第一段階として、自分自身の理解の確認のためにリーマン面の具体例を構成していきたいと思っています。今回はその前段として「リーマン面の定義」を丁寧にまとめていきたいと思います。
なお、今回の記事では「わかりやすく伝える」という意図はあまりなく、ただただ実直に定義を理解しようという考えで書いています。その点はご理解ください。
定義
のある開被覆
と、各
に対して
の開集合への同相写像
を考える。
と
の組が次を満たすとき、
はリーマン面であるという:
は正則関数
※単に「 はリーマン面である」ともいう。
長い条件でしたが、上記の条件をすべて満たすものがリーマン面です。リーマン面の具体例として対象 を作る際には、対象
がこの条件をすべて満たすかどうか確認する必要があります。私たちが示すべき目標を列挙したものといえます。
しかしながら、リーマン面の定義は、簡単なものではありません。条件がかなり多く、ただちに意味を捉えるのが難しいですね。丁寧に一つひとつ条件を確認しましょう。
①  は位相空間
は位相空間
まず、「 は位相空間である」ことを示す必要があります。位相空間の定義はここでは省略します。
「 は位相空間である」を示すためには、
の開集合系を決定するなどの方法があります。ほかにも、別の位相空間を定義してから、その位相空間から誘導される位相を考えることもあります。次回具体的な例を作る際には、後者の方法をとりたいと思いますが、具体的な方法についてはそのときに議論しましょう。
②  は第二可算公理を満たす
は第二可算公理を満たす
の開集合全体を
として、そのある部分集合
をとります(「
のいくつかの開集合」を元とするような集合)。
の任意の開集合
が、
の部分集合
の合併によって表せるとき、つまり
が成り立つとき、 を
の開基といいます。開基は、
の任意の開集合を合併によって「生成する」ようなものだというわけですね。
が「高々可算個」の開基をもつとき、
は第二可算公理を満たすといいます。
の開集合全体
を考えれば、
は定義から明らかに開基であるわけですが、場合によっては
は連続濃度になってしまうこともあります。
より濃度の小さい可算個の集合を使ってうまいこと
が表現できる場合は、第二可算公理を満たすというわけですね。
長々と書いてきましたが、多くの素性のよい空間は、第二可算公理を満たすそうなので、この条件についてはあまり神経質になる必要はなさそうです。
③  は連結
は連結
任意の位相空間において、 自身と空集合
は開集合かつ閉集合です。開集合かつ閉集合であることを開かつ閉といったりします。
ここで、 が
と
以外に開かつ閉な部分集合をもたないとき、
は連結であるといいます。
連結の定義から「連結」のイメージが湧きづらいかもしれません。同値な定義として、 の任意の開集合
について
が成り立つとき、 は連結であるといいます。
つまり、2枚の開集合によって を被覆したとき、必ず共通部分を持つということですね。常に「のりしろ」があるというわけですが、これは
が「連結している感じ」がするのではないでしょうか。
逆に、連結していない場合、たとえば2つの部分に離れてしまっている場合は開集合2枚で を被覆して、かつ共通部分をとらない(分離させる)ことができてしまいますね。
④  はハウスドルフ
はハウスドルフ
位相空間 がハウスドルフであるとは、
の任意の2点
に対して、
となるような
の開近傍
が存在するということです。
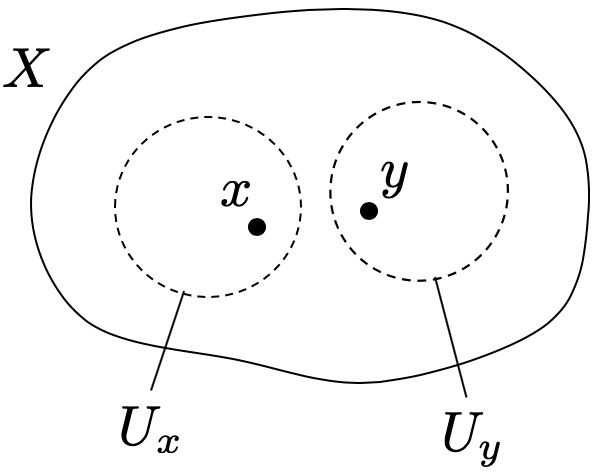
「2点が近傍によって分離できる」というのは素朴でイメージしやすい性質ですが、 がハウスドルフであることを示すのは簡単ではない場合が多そうです。
⑤  は
は  の開被覆
の開被覆
位相空間 が、
のある開集合系
の合併によってかけるとき、
を開被覆と呼びます。
はインデックス集合で、無限個でも構いません。
つまり、ある開被覆が存在することを示す必要があるということですね。(任意の開被覆ではなく、一つ都合のよい開被覆があればよいことに注意しましょう。)
⑥  の開集合への同相写像
の開集合への同相写像 
上で定めた開被覆の各開集合 に対して、「
の開集合への同相写像
」とは、
のある開集合
に対して、同相写像
を考えるということですね。この と
の組
を座標近傍系といい、今考えている座標近傍系全体の集合
をアトラスといいます。
同相写像 の行き先は
ということで、
の各点には複素数の値が定まります。したがって、
の一部分に、
を通して
による座標が貼り付けられるということです。

の開被覆に属するすべての開集合に対して座標近傍系が定義されているので、
の各点に座標が定まったといえます。
また、座標近傍系は、今考えている特定の開被覆に対して定めれば十分であることに注意します。
なお、 が同相写像であるとは、
が次の3つの条件を満たすことをいいます。
が全単射
が連続写像
が連続写像
さらっと「同相写像である」と書いていましたが、条件を示すのが結構大変だとわかるでしょう。
⑦  は正則関数
は正則関数
上によって、 には各点に対して座標が定まったわけです。局所的には座標が定まっていますが、それが全体的に「うまくいっている」かどうか考える必要があります。
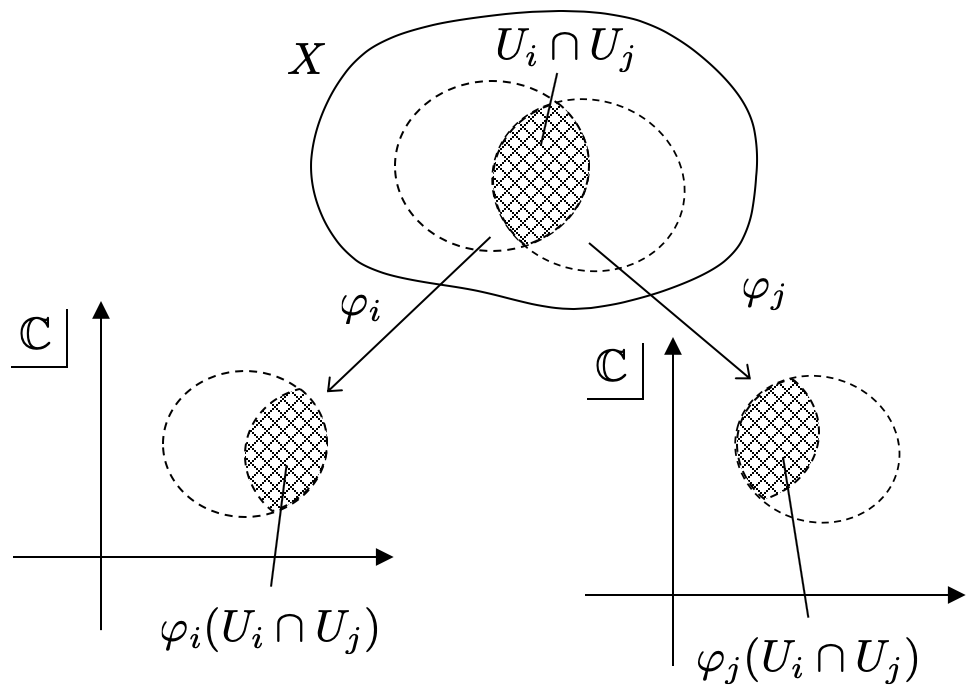
共通部分を持つ開被覆 を考えたときに、
にはそれぞれ異なる座標近傍系
が定まっています。つまり、共通部分
には
という2通りの座標近傍系が定まっているわけですね。リーマン面の条件⑦では、これらの座標近傍系の間の「整合性」を要請しています。
この整合性についてより詳しく説明したいと思います。 を
によって写したものをそれぞれ
と書くことにします。これらはどちらも
の開集合で、
と同相です。
よって、次のような合成写像を考えることができます。 の逆写像
によって
を
に戻します。さらに、
によって
を
に写します。この合成写像を
とします。
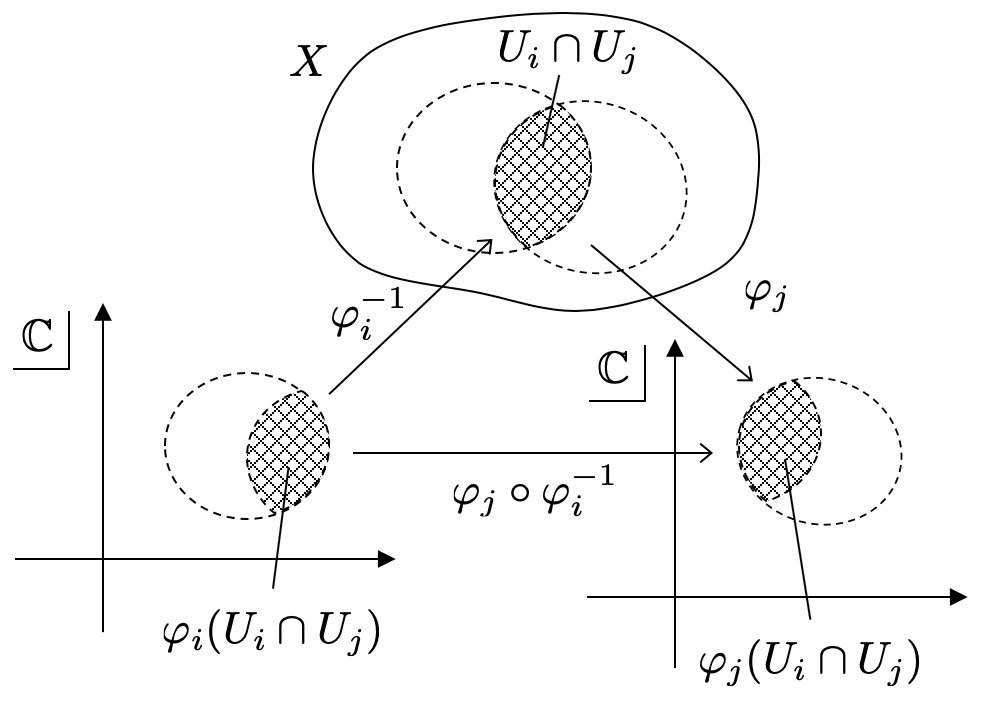
構成からわかるように、 は
の開集合から
の開集合への写像となっていますね。つまり、単なる複素関数になります。
条件⑦では、複素関数 が正則であることを要請しているというわけです。
リーマン面と多様体の関係
多様体のことを知っている人は、リーマン面の定義が多様体の定義に似ていることに気づいたと思います。
実際、上の定義で となっているところを
に置き換えて、「正則関数」のところを「連続関数(あるいは無限回微分可能)」と置き換えると「
次元多様体(あるいは
次元可微分多様体)」の定義そのものになります。
は
だと思えて、正則関数は連続関数なので、リーマン面は2次元の多様体となります。
一方、 のところを
に置き換えると、これは
次元複素多様体の定義となります。リーマン面は1次元複素多様体だということができます。
おわりに
以上がリーマン面の定義で主張していることの全容です。ある与えられた がリーマン面であることを示すためには、上記の条件①~⑤がすべて成り立つことを言う必要があります。
次回は、このことを具体的に で確認したいと思います。リーマン面の定義を丁寧にすべて確認していくのは、相当に骨が折れます。リーマン面の練習として、頑張って全部の条件を示したいと思います。
それでは今日はこの辺で。
2020.12.24追記
リーマン面の定義について誤解があった部分を修正しました。

2021.03.07追記
リーマン面の定義に「連結」の条件が入っていなかったので、追記しました。合わせて連結性の定義の説明を追記しました。
2021.03.08追記
「局所座標系」と書いていた部分を「座標近傍系」という呼び方に変えました。局所座標系はまた別の概念を呼ぶときに使いたいと思います。
