アフィンスキームとは何だろうか(3) - tsujimotterのノートブック

この記事は、シリーズ記事「アフィンスキームとは何だろうか」の第３回の記事です。

前回はついにアフィンスキームを定義しました。今日は、本シリーズの最後の記事として、アフィンスキームの間の射を定義したいと思います。

アフィンスキームの射を通して「 $\text{Spec}(\mathbb{Z})$ 上のスキーム」などの概念を考えることができ、これにより整数論についての面白い見方を得ることができます。

本記事の目次：

6. アフィンスキームの射

位相空間の間の射

構造層の間の射

アフィンスキームの間の射

7. アフィンスキームの射の具体例

Z[√-1] の素イデアル分解法則

代数曲線の還元

可換環の圏とアフィンスキームの圏

8. まとめ

振り返り

感想

参考文献

6. アフィンスキームの射

代数多様体の間に射があったように、アフィンスキームの間にも射を定義できます。その射は、環準同型写像から誘導されます。

位相空間の間の射

可換環 $A, B$ があったときに、その間に環準同型写像 $\varphi\colon A \to B$ があるとします。このとき、 $\boldsymbol{X} = \text{Spec}(B)$ から $\boldsymbol{Y} = \text{Spec}(A)$ に向けた、 $\varphi$ の方向とは逆向きの射 $f\colon \boldsymbol{X} \to \boldsymbol{Y}$ が誘導されます。このことについて示しましょう。

$\varphi$ によって、 $B$ の素イデアル $\mathfrak{q}$ の中に写る $A$ の元全体を $\varphi^{-1}(\mathfrak{q})$ と書きましょう。 $\varphi^{-1}(\mathfrak{q})$ が $A$ の素イデアルであることを示します。

$ab \in \varphi^{-1}(\mathfrak{q}) \Longrightarrow a \in \varphi^{-1}(\mathfrak{q})$ または $b \in \varphi^{-1}(\mathfrak{q})$ を示せば良い。

$\varphi(ab) \in \mathfrak{q}$ であり、 $\varphi(ab) = \varphi(a)\varphi(b) \in \mathfrak{q}$ であるから、 $\mathfrak{q}$ は $B$ の素イデアルより $\varphi(a) \in \mathfrak{q}$ または $\varphi(b) \in \mathfrak{q}$ である。よって、 $a \in \varphi^{-1}(\mathfrak{q})$ または $b \in \varphi^{-1}(\mathfrak{q})$ であることが言えたので、 $\varphi^{-1}(\mathfrak{q})$ は $A$ の素イデアル。

$\mathfrak{q} \in \boldsymbol{X}$ に対して $f(\mathfrak{q}) := \varphi^{-1}(\mathfrak{q}) \in \boldsymbol{Y}$ を対応させることで、 $f \colon \boldsymbol{X} \to \boldsymbol{Y}$ が定まります。この $\varphi$ から誘導された写像 $f$ は、位相空間の間の連続写像になることも（要証明ですが）確認できます。

構造層の間の射

アフィンスキームの射というときは、単に $f\colon \boldsymbol{X} \to \boldsymbol{Y}$ だけではダメで、構造層についての射も定義する必要があります。 $\varphi\colon A \to B$ に対して、層についての射

$f^{\#}\colon \mathcal{O}_{\boldsymbol{Y}} \to f_{*}\mathcal{O}_{\boldsymbol{X}}$

も誘導されます。ここで $f_{*}\mathcal{O}_{\boldsymbol{X}}$ は、次のように定義します。

$\boldsymbol{X}, \boldsymbol{Y}$ の開集合をそれぞれ $V, U$ とし、 $\mathcal{O}_{\boldsymbol{X}}(V)$ の元 $s$ を考えます。 $s$ は定義より $V$ 上の正則関数です。

また、位相空間 $\boldsymbol{X}, \boldsymbol{Y}$ の間の連続写像 $f\colon \boldsymbol{X} \to \boldsymbol{Y}$ の逆像 $f^{-1}$ は、連続写像の定義より $\boldsymbol{Y}$ の開集合 $U$ を $\boldsymbol{X}$ の開集合 $V$ に移します。よって、 $f^{-1}$ に $s$ を合成した $s\circ f^{-1}$ は $U$ 上の正則関数になります。

$s\circ f^{-1}$ 全体のなす環を $f_{*}\mathcal{O}_{\boldsymbol{X}}(U)$ と定義します。

これにより、開集合 $U \subset \boldsymbol{Y}$ に対して $f_{*}\mathcal{O}_{\boldsymbol{X}}(U)$ を割り当てるルールが構成できました。 $f_{*}\mathcal{O}_{\boldsymbol{X}}$ は $\boldsymbol{Y}$ 上の層であることもわかります。

あとは、 $\varphi$ から誘導される写像 $f^{\#}$ が、 $\boldsymbol{Y}$ 上の層の射であることを示す必要があります。ここで層の射であることは示さないですが、層の射の定義は確認しておきましょう。

$\boldsymbol{Y}$ 上の2つの層の間の射 $f^{\#}\colon \mathcal{F} \to \mathcal{G}$ とは、開集合 $U \subset \boldsymbol{Y}$ に対する層の切断 $\mathcal{F}(U), \mathcal{G}(U)$ の間の環準同型写像

$f^{\#}(U)\colon \mathcal{F}(U) \to \mathcal{G}(U)$

であって、2つの開集合 $U, V$ が包含関係 $V\subset U$ にあるとき、以下の可換図式を満たす写像のことです。

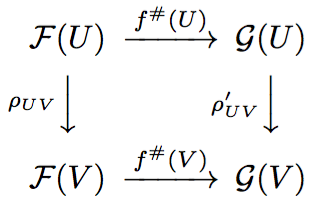
$\rho_{UV}, \rho'_{UV}$ はそれぞれ $\mathcal{F}, \mathcal{G}$ の制限写像です。

これで、構造層の間の射が定義できました。

アフィンスキームの間の射

以上定義した

$\begin{align*} f &\colon \boldsymbol{X} \to \boldsymbol{Y} \\ f^{\#} &\colon \mathcal{O}_{\boldsymbol{Y}} \to f_{*}\mathcal{O}_{\boldsymbol{X}} \end{align*}$

を合わせて

$(f, f^{\#}) \colon (\boldsymbol{X}, \mathcal{O}_{\boldsymbol{X}}) \to (\boldsymbol{Y}, \mathcal{O}_{\boldsymbol{Y}})$

と表記して、射の組 $(f, f^{\#})$ をアフィンスキームの射といいます。

例によって、 $f\colon \boldsymbol{X} \to \boldsymbol{Y}$ だけを表記してアフィンスキームの射ということもありますが、実際は層の間の射も考えています。単に省略しているだけなので注意してください。

可換環 $S$ に対して $S \to A$ なる環準同型があるとき、アフィンスキームの間に $\text{Spec}(A) \to \text{Spec}(S)$ なる射が誘導されます。このとき、 $\text{Spec}(A)$ は $S$ 上のアフィンスキームといいます。

任意の可換環 $A$ に対して、 $\mathbb{Z}$ からの環準同型が入りますので、任意のアフィンスキーム $\text{Spec}(A)$ は $\mathbb{Z}$ 上のアフィンスキームになります。

7. アフィンスキームの射の具体例

さて、アフィンスキームの射の具体例について考えてみましょう。

$\mathbb{Z} \to \mathbb{Q}$ の間に $\varphi \colon n \mapsto n/1$ で定まる環準同型によって、アフィンスキームの射 $f\colon \text{Spec}(\mathbb{Q}) \to \text{Spec}(\mathbb{Z})$ が誘導されます。 $\text{ker}(\varphi) = (0)$ より、射 $f$ は $(0) \in \text{Spec}(\mathbb{Q})$ に対して $(0) \in \text{Spec}(\mathbb{Z})$ を対応させる写像となります。

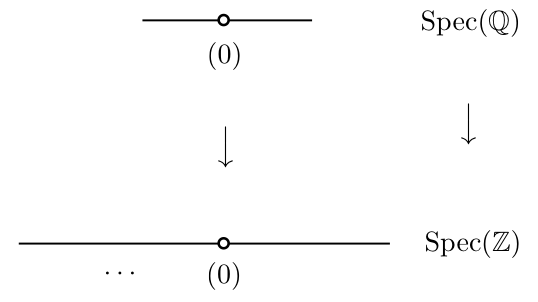
次の例です。 $\mathbb{Z} \to \mathbb{F}_p$ の間に $\varphi\colon n \mapsto n \pmod{p}$ で定まる環準同型によって、アフィンスキームの射 $\text{Spec}(\mathbb{F}) \to \text{Spec}(\mathbb{Z})$ が誘導されます。 $\text{ker}(\varphi) = (p)$ より、射 $f$ は $(0) \in \text{Spec}(\mathbb{F}_p)$ に対して $(p) \in \text{Spec}(\mathbb{Z})$ を対応させる写像となります。

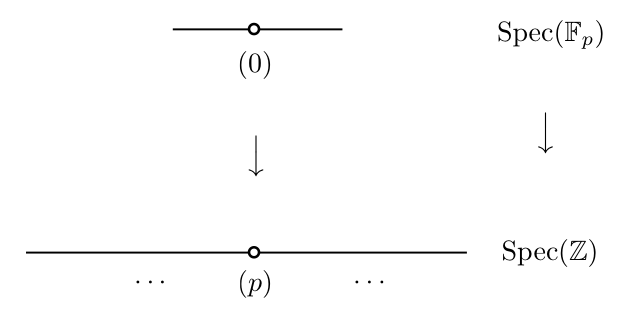
上の図からわかるように、 $\text{Spec}(\mathbb{Z})$ の点 $(0)$ の上には $\text{Spec}(\mathbb{Q})$ が、 $\text{Spec}(\mathbb{Z})$ の点 $(p)$ の上には $\text{Spec}(\mathbb{F}_p)$ が乗っていると見ることができますね。

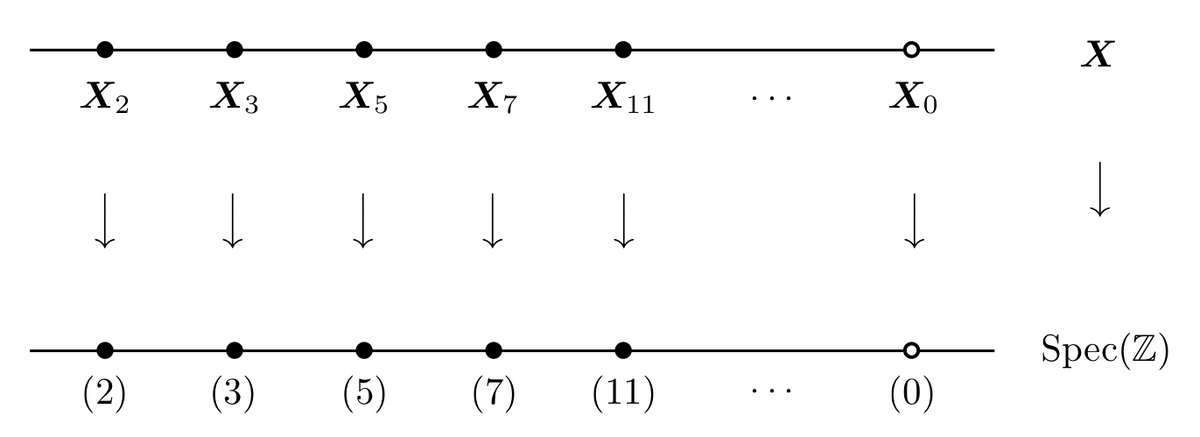
Z[√-1] の素イデアル分解法則

上の例は割と自明な例でしたが、次は面白い例です。

アフィンスキームとして、 $\boldsymbol{X} = \text{Spec}(\mathbb{Z}[\sqrt{-1}])$ を考えましょう。 $\boldsymbol{X}$ の点は、 $\mathbb{Z}[\sqrt{-1}]$ の素イデアル全体となります。たとえば $(2 + 3\sqrt{-1})$ のような元ですね。

環準同型 $\mathbb{Z} \to \mathbb{Z}[\sqrt{-1}]$ が埋め込み写像 $\varphi\colon n \mapsto n$ によって定まるので、 $\boldsymbol{X}$ は $\mathbb{Z}$ 上のスキームです。

まず $\text{ker}(\varphi) = (0)$ より、 $(0) \in \boldsymbol{X}$ は $(0) \in \text{Spec}(\mathbb{Z})$ に写ります。

次に $\mathfrak{q} = (2 + 3\sqrt{-1})$ を考えると、 $\varphi$ によって $(2 + 3\sqrt{-1})$ に写る $\mathbb{Z}$ の元全体は、 $(2 + 3\sqrt{-1}) \cap \mathbb{Z}$ となります。これはすなわち $\mathbb{Z}$ の素イデアル $(13)$ です。よって、 $(2 + 3\sqrt{-1}) \in \boldsymbol{X}$ は $(13) \in \text{Spec}(\mathbb{Z})$ に写ります。

同様に、 $(2 - 3\sqrt{-1}) \in \boldsymbol{X}$ も $(13) \in \text{Spec}(\mathbb{Z})$ に写ります。

これらは両方とも $(13)$ を $\mathbb{Z}[\sqrt{-1}]$ で素イデアル分解したときに得られる素因子となっています。

$(13) = (2 + 3\sqrt{-1})(2 - 3\sqrt{-1})$

少しだけ、 $\mathbb{Z}[\sqrt{-1}]$ における素イデアル分解について復習しましょう。

一般に、 $\mathbb{Z}$ の素イデアル $(p)$ は $\mathbb{Z}[\sqrt{-1}]$ で素イデアル分解されますが、そのとき

$(p) = \mathfrak{q}_1^{e_1}\mathfrak{q}_2^{e_2}$

と書くことができます。

$p \equiv 1 \pmod{4}$ のとき

$(p) = \mathfrak{q}_1\mathfrak{q}_2$

と書けることが知られていて、このとき $(p)$ は $\mathbb{Z}[\sqrt{-1}]$ で完全分解するといいます。

また、 $p \equiv 3 \pmod{4}$ のとき

$(p) = \mathfrak{q}$

と書けて、 $(p)$ は $\mathbb{Z}[\sqrt{-1}]$ で惰性するといいます。

$p = 2$ のときは

$(p) = \mathfrak{q}^2$

と書けて、 $(p)$ は $\mathbb{Z}[\sqrt{-1}]$ で分岐するといいます。

いずれの場合でも、 $(p)$ の素因子を $\mathfrak{q}$ としたとき $(p) = \mathfrak{q} \cap \mathbb{Z}$ が成り立ちます。したがって、 $\mathfrak{q} \in \boldsymbol{X}$ はアフィンスキームの射によって $(p)$ に写ります。

アフィンスキームの射 $f$ によって $(p)$ に写る $\boldsymbol{X}$ の元全体を $(p)$ のファイバー $f^{-1}( (p) )$ といいますが、これを使って以下のように言い換えることができます。

$p \equiv 1 \pmod{4}$ のとき、 $(p)$ のファイバーは $f^{-1}( (p) ) = \{\mathfrak{q}_1, \mathfrak{q}_2\}$
$p \equiv 3 \pmod{4}$ のとき、 $(p)$ のファイバーは $f^{-1}( (p) ) = \{\mathfrak{q}\}$
$p = 2$ のとき、 $(p)$ のファイバーは $f^{-1}( (p) ) = \{\mathfrak{q} \}$

ファイバーとは、毛穴 $(p)$ から生えている毛の集まりみたいなものを想像してもらえるといいかと思います。

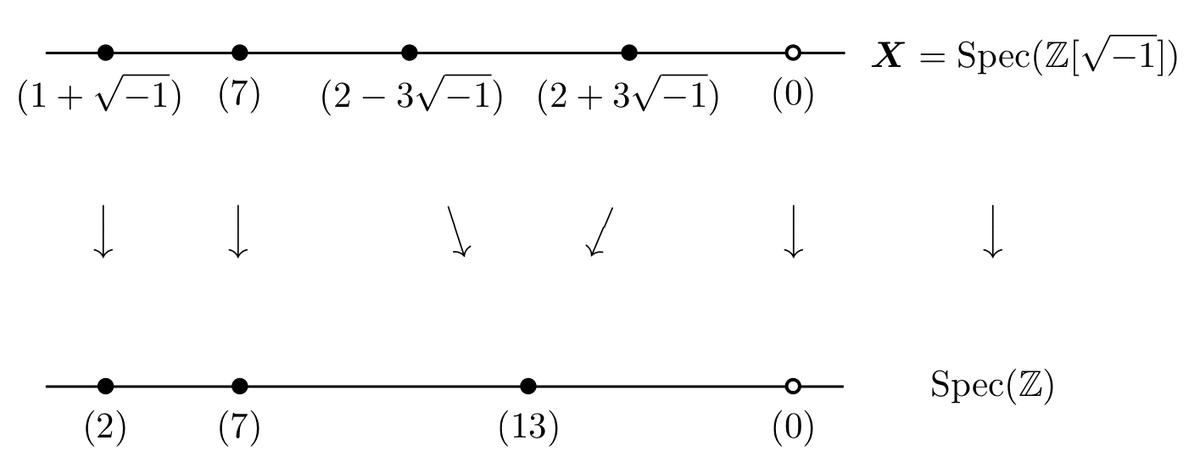
分岐・不分岐・完全分解の様子が、アフィンスキームの言葉によって見事に表現されていますね。いつも書いていた素イデアル分解の図は、実はアフィンスキームの間の射を表現したものだったのかと思わされます。

代数曲線の還元

もう一つ面白い例として、代数曲線の還元を考えましょう。

2変数多項式環のイデアル $I \subset \mathbb{Q}[X, Y]$ を考えて、 $I$ で定義される代数多様体を考えます。 $I = (Y^2 - X^3 + X)$ とすると、 $V = V(I)$ は楕円曲線 $Y^2 = X^3 - X$ になります。

$\mathbb{Q}$ 上の曲線は、係数の分母を払うことで整数係数にできます。実際、 $Y^2 - X^3 + X$ は整数係数です。そこで、アフィンスキーム $\boldsymbol{X} = \text{Spec}(\mathbb{Z}[X, Y]/(Y^2 - X^3 + X))$ を考えることができます。

$\mathbb{Z}$ から $\mathbb{Z}[X, Y]/(Y^2 - X^3 + X)$ への環準同型 $n \mapsto n$ が存在するので、 $\boldsymbol{X}$ は $\mathbb{Z}$ 上のアフィンスキームとみなせます。

この環準同型が誘導するアフィンスキームの射 $f\colon \boldsymbol{X} \to \text{Spec}(\mathbb{Z})$ について、 $\text{Spec}(\mathbb{Z})$ の点 $(p)$ におけるファイバー $f^{-1}( (p) )$ を考えてみましょう。

そのために、ファイバー積という概念を導入します。

$\boldsymbol{S}$ をアフィンスキームとして、 $\boldsymbol{S}$ 上のアフィンスキーム $\boldsymbol{X}, \boldsymbol{Y}$ を考えます。このとき、 $\boldsymbol{X}, \boldsymbol{Y}$ の $\boldsymbol{S}$ 上のファイバー積 $\boldsymbol{X} \times_{\boldsymbol{S}} \boldsymbol{Y}$ が次のように定義されます。 $\boldsymbol{X} \times_{\boldsymbol{S}} \boldsymbol{Y}$ はアフィンスキームで、 $p_1 \colon \boldsymbol{X} \times_{\boldsymbol{S}} \boldsymbol{Y} \to \boldsymbol{X}$ および $p_2 \colon \boldsymbol{X} \times_{\boldsymbol{S}} \boldsymbol{Y} \to \boldsymbol{Y}$ があり、 $\boldsymbol{X} \to \boldsymbol{S}$ および $\boldsymbol{Y} \to \boldsymbol{S}$ と可換図式をなす。このようなものの中で普遍的なものが $\boldsymbol{X}, \boldsymbol{Y}$ のファイバー積 $\boldsymbol{X} \times_{\boldsymbol{S}} \boldsymbol{Y}$ であり、同型を除いて一意に定まります。

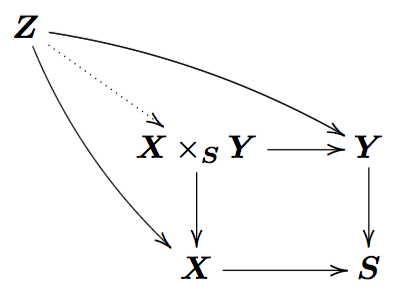
上の楕円曲線の場合を考えましょう。 $\boldsymbol{X} = \text{Spec}(\mathbb{Z}[X, Y]/(Y^2 - X^3 + X))$ として、 $\boldsymbol{Y} = \text{Spec}(\mathbb{F}_p)$ とすると、 $\boldsymbol{X}, \boldsymbol{Y}$ はそれぞれ $\boldsymbol{S} = \text{Spec}(\mathbb{Z})$ 上のアフィンスキームです。 $\boldsymbol{X}, \boldsymbol{Y}$ に対し、 $\text{Spec}(\mathbb{Z})$ 上のファイバー積 $\boldsymbol{X}_p := \boldsymbol{X} \times_{\text{Spec}(\mathbb{Z})} \text{Spec}(\mathbb{F}_p)$ は以下の可換図式により定まります。

$\boldsymbol{X}_p$ は $\text{Spec}(\mathbb{F}_p)$ 上のアフィンスキームであり、 $\text{Spec}(\mathbb{F}_p)$ は $\text{Spec}(\mathbb{Z})$ の点 $(p)$ の上に乗っていますから、 $(p)$ の上には $\boldsymbol{X}_p$ が乗っていることがわかります。

この $\boldsymbol{X}_p = \boldsymbol{X} \times_{\text{Spec}(\mathbb{Z})} \text{Spec}(\mathbb{F}_p)$ は具体的に何なのでしょうか。

実はこれは $\text{Spec}(\mathbb{Z}[X, Y]/(Y^2 - X^3 + X) \otimes_{\mathbb{Z}} \mathbb{F}_p)$ であることがわかります。

また、 $\otimes_{\mathbb{Z}} \mathbb{F}_p$ するということは、係数を $\mathbb{F}_p$ に置き換えるということなので、

$\boldsymbol{X}_p = \text{Spec}(\mathbb{F}_p[X, Y]/(Y^2 - X^3 + X) )$

であることが言えます。

右辺は楕円曲線 $Y^2 = X^3 - X$ の係数を $\mathbb{F}_p$ に置き換えた曲線に相当しますが、このような曲線を得る操作を $p$ における還元といいます。

つまり、アフィンスキームの射 $f\colon \boldsymbol{X} \to \text{Spec}(\mathbb{Z})$ における $(p)$ のファイバー $f^{-1}( (p) )$ は、曲線 $\boldsymbol{X}$ の $p$ における還元となっているわけですね。

なお、 $(0) \in \text{Spec}(\mathbb{Z})$ のファイバーは、 $\boldsymbol{X}_0 := \text{Spec}(\mathbb{Q}[X, Y]/(Y^2 - X^3 + X) )$ となり、 $\mathbb{Q}$ 上の曲線が乗っていることになります。

このように、 $\boldsymbol{X} = \text{Spec}(\mathbb{Z}[X, Y]/(Y^2 - X^3 + X))$ には、標数 $p$ の体の係数を持つ曲線や標数 $0$ の体の係数を持つ曲線がたくさん乗っているような構造をしているということですね。面白いです。

可換環の圏とアフィンスキームの圏

最後に、アフィンスキームの圏における重要な性質を紹介します。

可換環を対象として、射を環準同型写像とする圏を可換環の圏 ${\bf cRing}$ とします。また。アフィンスキームを対象とし、射としてアフィンスキームの射を考える圏をアフィンスキームの圏 ${\bf Affine}$ とします。

このとき、 ${\bf cRing}$ と ${\bf Affine}$ は圏同値であることが示されます。

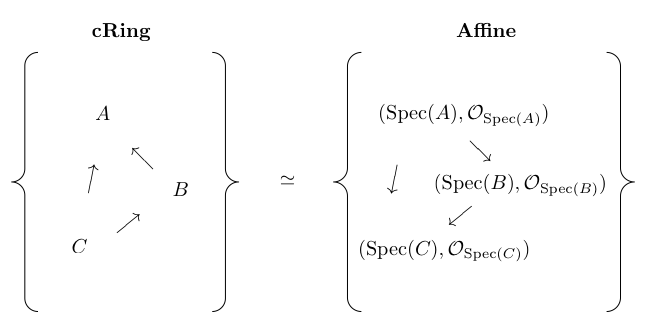
つまり、可換環とアフィンスキームは、圏として見たときには同じ情報を持っているということですね。

可換環の圏の上で考えている整数論の問題を、アフィンスキームの圏に移してから、幾何的な道具を使って解いて元に戻すということもできるようになるかもしれません。

8. まとめ

「アフィンスキームとは何だろうか」と題して、３回に渡ってシリーズ記事を書いてきました。簡単に振り返りつつ、感想を述べることにしましょう。

振り返り

第１回の記事では、代数幾何の基本的な話の紹介を通して、素イデアルを点とする空間「環のスペクトル」に至る流れを紹介しました。この「素イデアルだけで空間だと思う」という発想は、最初は奇抜に思えるのですが、ヒルベルトの零点定理の話を踏まえると納得がいくということでした。

さらに、環のスペクトルにザリスキー位相なる位相を入れ、位相空間を構成しました。ザリスキー位相は、イデアルの包含関係に基づいて開集合を作るのですが、一見あまり直感的ではないと感じてしまいます。実際のところは、イデアルと図形の対応関係を考えると、イデアルの包含関係はそのまま代数的集合の間の包含関係に対応するので、代数的集合の包含関係に合わせて位相を入れたのだと思うと、実はそれほど不思議なものではないと思います。この辺は、本文ではあまり強調しなかったので、ここで触れておきます。

第２回の記事では「構造層」を定義しました。環のスペクトルの開集合上で定義される正則関数を考えて、開集合に「正則関数全体のなす環」を対応させる反変関手を構造層というのでした。環のスペクトルを構成するために使った可換環 $A$ の元の有理式を、環のスペクトル上の「関数」と思うことができるというのが、私は面白いと感じました。

位相と構造層が定まったので、環のスペクトルと構造層の組として「アフィンスキーム」を定義することができました。体 $K$ の例のように、環のスペクトルだけでは互いに区別できないケースもあるため、構造層は必要だという話もありました。

第３回では「アフィンスキームの射」を定義しました。アフィンスキームの射を用いると、可換環の間の関係性を、次のようなイメージで捉えることができました。

$\text{Spec}(\mathbb{Z})$ の各点には、 $\text{Spec}(\mathbb{F}_p)$ や $\text{Spec}(\mathbb{Q})$ が乗っている
代数体の素イデアル分解法則は、まさにアフィンスキームの射の様子を表している
代数曲線で用いられる「 $\bmod{p}$ における還元」という操作が、スキームの射のファイバーをとることで得られる

最後に、アフィンスキームの圏が可換環の圏と「圏同値」であることについても触れました。「アフィンスキームは元の可換環の情報を忘れていない」ということが示唆されました。

感想

スキームや代数幾何について勉強しようと思ったきっかけは、年初めのこのツイートでした。

Specとかアフィンスキームとかについて、自分なりに初めて納得がいった（かもしれない）記念。図がめっちゃ汚いけどもうれしくて撮った pic.twitter.com/hNZDWSIIdP
— tsujimotter 日曜数学者 (@tsujimotter) 2018年1月1日

なんとなくコホモロジー [2] の本を読んでいた中で、スキームの射についての直感的な理解が得られた気がしたのです。もう少し頑張ったらわかりそうだと思いました。これがきっかけとなり、年明けから代数幾何を少しずつ勉強するようになりました。この「もう少しでわかるかもしれない」という感覚はとても大事だと思っていて、こういう感覚があるからこそ勉強しようというモチベーションが生まれてくるのだと思います。

３月ぐらいには「層」についての具体例を計算する中で一つの発見がありました。この２つの出来事が後押しして、ここまで書いてきました。まだ理解不足な部分もありますが、これだけの分量の記事を自分の言葉でまとめられたことが嬉しいです。

代数幾何の勉強を通してよかったことはもう一つあります。それは「可換環論の重要性」に気づいたことです。

今回の記事の中にも、ところどころに「イデアル」「環の局所化」「テンソル積」といったキーワードが出てきましたが、これらは可換環論における用語です。これらの用語については以前から知っていたものの、何のために勉強する必要があるのか正直よくわかっていませんでした。代数幾何において必要だということを知り、可換環論そのものを学ぶモチベーションが出てきました。

長くなりましたが、以上で「アフィンスキーム」についての解説を終わりにします。まだまだ基本的な部分しか理解していませんが、引き続き勉強を進めていきたいと思います。

それでは今日はこの辺で。