最近、スキームの話をきっかけに、tsujimotterのノートブックにも「層」という概念が登場するようになりました。
ところが、これまでのブログ記事では、層の定義は頑なに避けられてきました。その理由は、私自身が理解できていなかったからです。
今回は、いよいよ層の定義をしてみたいと思います。今日のポイントは、具体例の計算です。具体例を通して、層の理解を目指しましょう。
目次:
前層(復習)
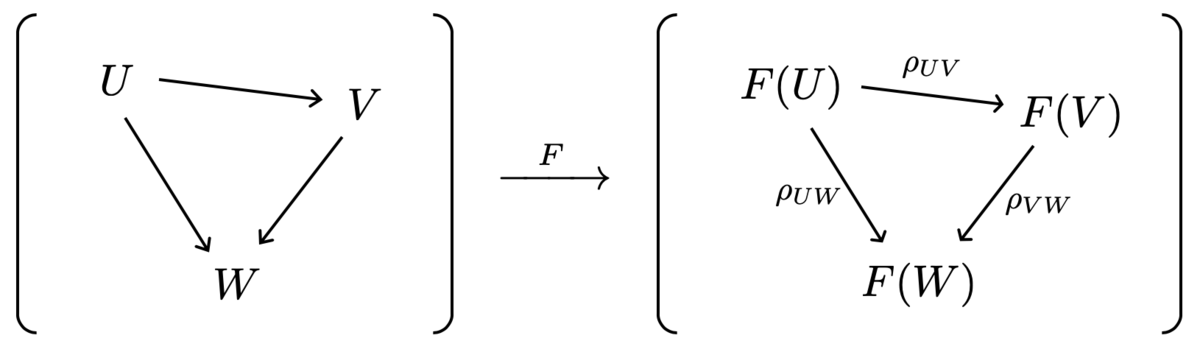
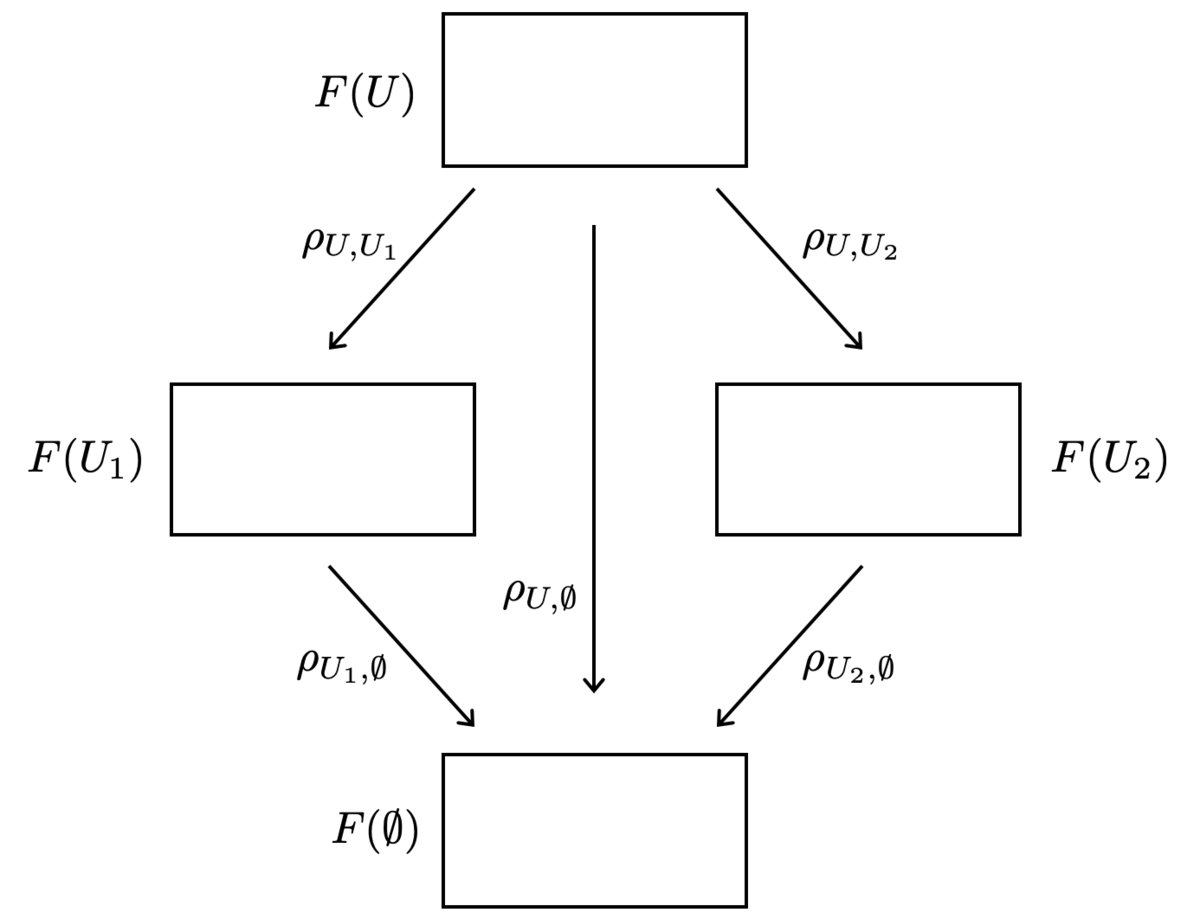
層は、後で述べる「ある特別な性質」を持った前層です。まずは前層の定義を丁寧に復習しましょう。
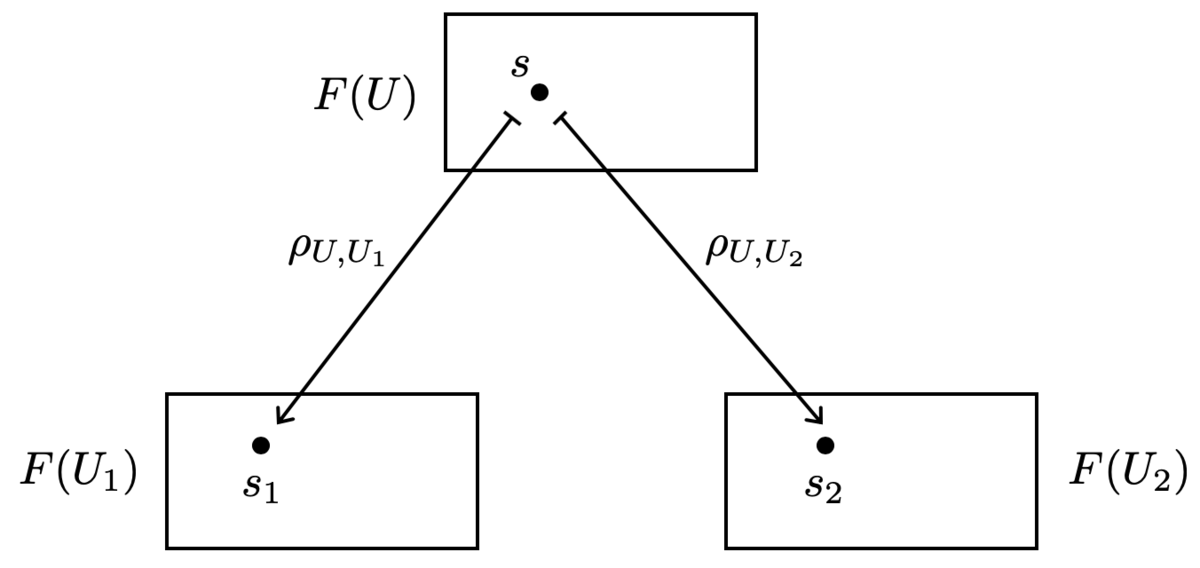
このとき、 から
への関手
を
上の(
への)前層という。
以前の記事では、関手の行き先の圏 を集合の圏
としていましたが、今回の記事では、すべてアーベル群の圏
とします。今回は
への前層のみを考えるので、以降「
への」という部分を省略することにします。
を
上の前層とします。
関手 は、
の開集合
をアーベル群
に対応させる関手です。層の理論では、
の元を一般に切断といいます。あとで切断の例として関数が出てきますが、一般には関数とは限りませんので切断と呼ぶわけです。
の対象
の間に射
があるとき(包含関係としては ということ)、関手
によって
と対応するアーベル群の準同型写像
を から
への制限写像 と呼びます。
制限写像には、関手の性質から において
なる射(包含関係としては
)があるときに、対応して以下の条件が成り立つことに注意しましょう。
また、恒等射 は、恒等射
に対応させます。
条件 を図で表すと以下のようになります。
制限写像の意味ですが、「開集合 に対して、
上で定義される(特定のクラスの)関数全体のなすアーベル群を割り当てる前層」を考えると、これはそのまま意味での制限写像となります。
でも触れているので参考になるかと思います。
前層の例
具体的に例を考えてみましょう。
たとえば を複素数平面
として、
上の任意の開集合
に対して、
として
を割り当てる関手 を考えます。この場合、
の任意の元
は、
上の正則関数です。
制限写像としては
に対して、
「制限」させて得られる正則関数
を与えます。
これが制限写像の条件 を満たします。
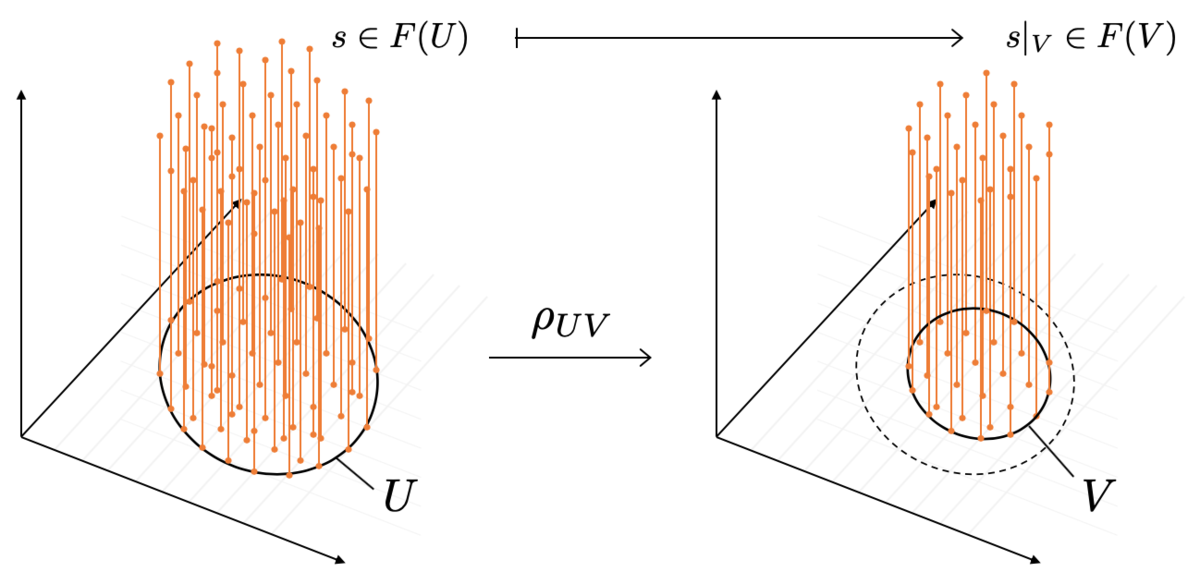
図は制限写像
よって、この は前層となります。
補足2で述べるように、 は層でもあります。
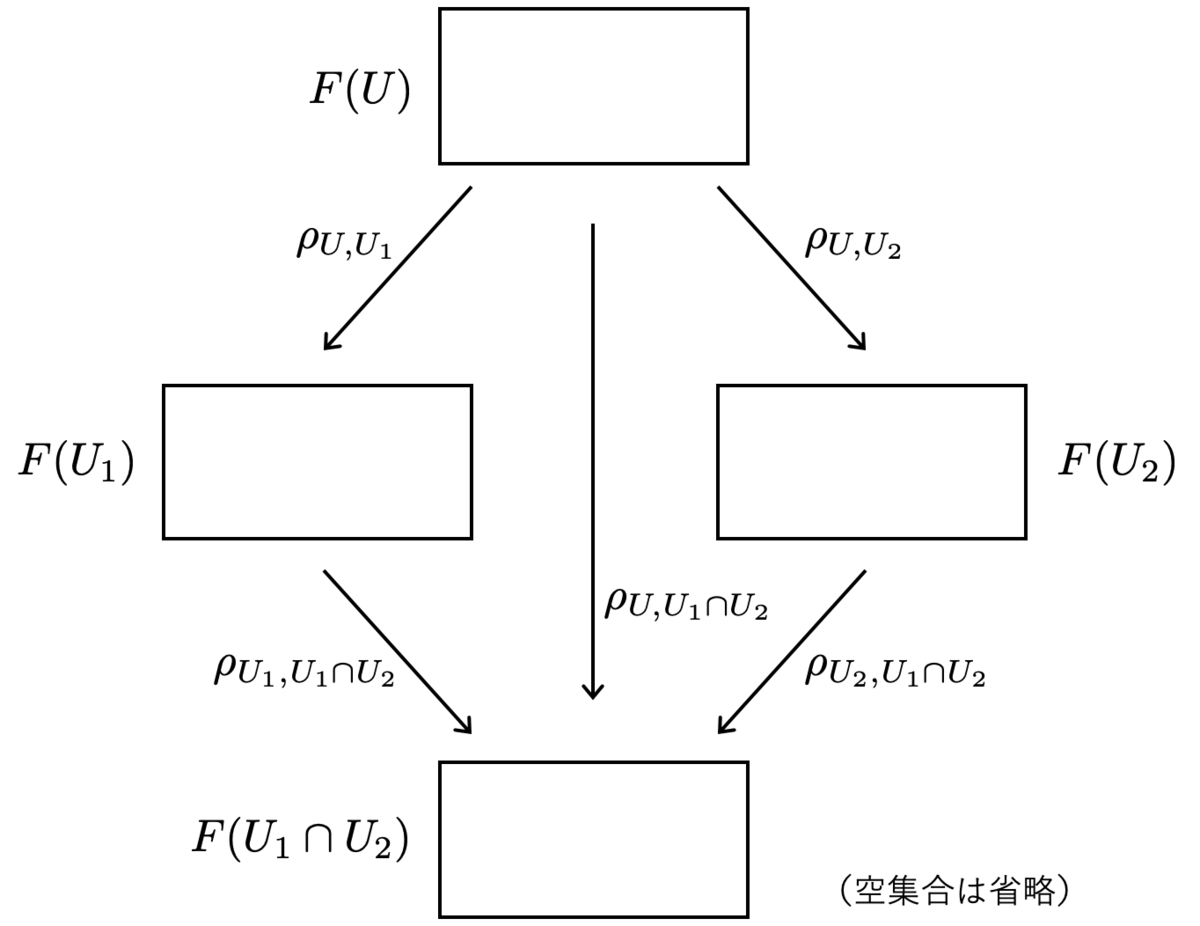
層の定義(2つの公理)
さて、本題はここからです。
まずは、よくわからないことを承知の上で、とりあえず層の定義を書き下してみましょう。
なる制限写像が与えられているとする。このとき、 の任意の開被覆
に対して、以下の公理1・公理2が成り立つとき、
を
上の層という。
- (公理1 既約性条件):
の元
が任意の
に対して
を満たすならば、常に が成立する。
- (公理2 閉条件):切断の族
が常に
をみたすものであるならば、常に の元
で
をすべての に対してみたすものが存在する。
はい。長かったですね。以上が層の定義です。
文章の構造としては、以下のようになっています。
- 前層
であるとする
が任意の開被覆に対して公理1・公理2を満たすならば、
は層である
公理を満たさなければ、単なる前層です。というわけで、層の定義においては、この2つの公理が本質的なわけですが・・・。
tsujimotterには、この2つの公理がまーーーーーーったくもってわからなかったのです。
正直言って意味不明でした。どちらもステートメントの意味がわからかったですし、何のためにこのような条件が課されているのかもわかりませんでした。
とはいえ、わからないとばかり言っていてもしょうがありません。どうにかして理解できないかと考えました。
いろいろ試行錯誤をしていくうちに、数学ガールという本の、とある有名なキャッチフレーズを思い出しました。
《例示は理解の試金石》
そうだ!
例示をしてみればわかるかもしれない!
そういうわけで、具体例の計算をしてみたのです。すると、不思議なことに、層の条件がなんだかわかってきた気がしました。
というわけで、私の計算した例をもとに、層について私が理解できたことを皆さんに共有できるよう、説明を試みたいと思います。
例1:共通部分を持たない開被覆
層の条件は任意の開被覆に対する条件となっているので、何かしら開被覆を考えましょう。
開集合 が
と、開集合
の合併によって表されているとします。この例では、簡単のため
と
の間に共通部分はないとします。図に表すと以下のようなものを考えていることになります。
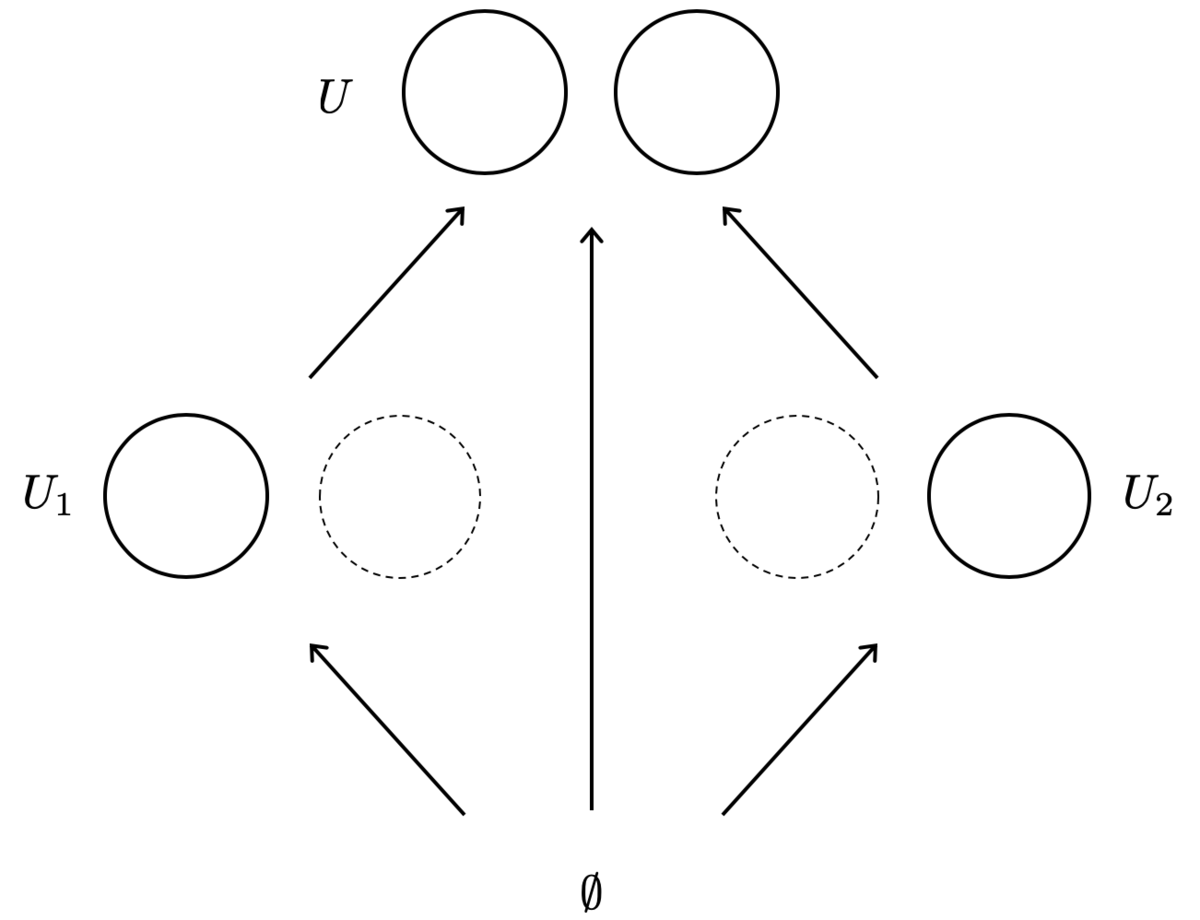
以上の状況に対して、層の2つの公理を一つずつ確かめていきましょう。
公理1:既約性条件
まず一つ目の条件を確認します。
を満たすならば、常に が成立する。
これを、現在の状況 に合わせて書き換えると、こうなります。
を満たすならば、常に が成立する。
だいぶ見やすくなりましたね。順を追って主張を確認します。
まず、この条件では には
という元があることを仮定しています。
この を、それぞれ制限写像
によって写したものを
、制限写像
によって写したものを
とします。
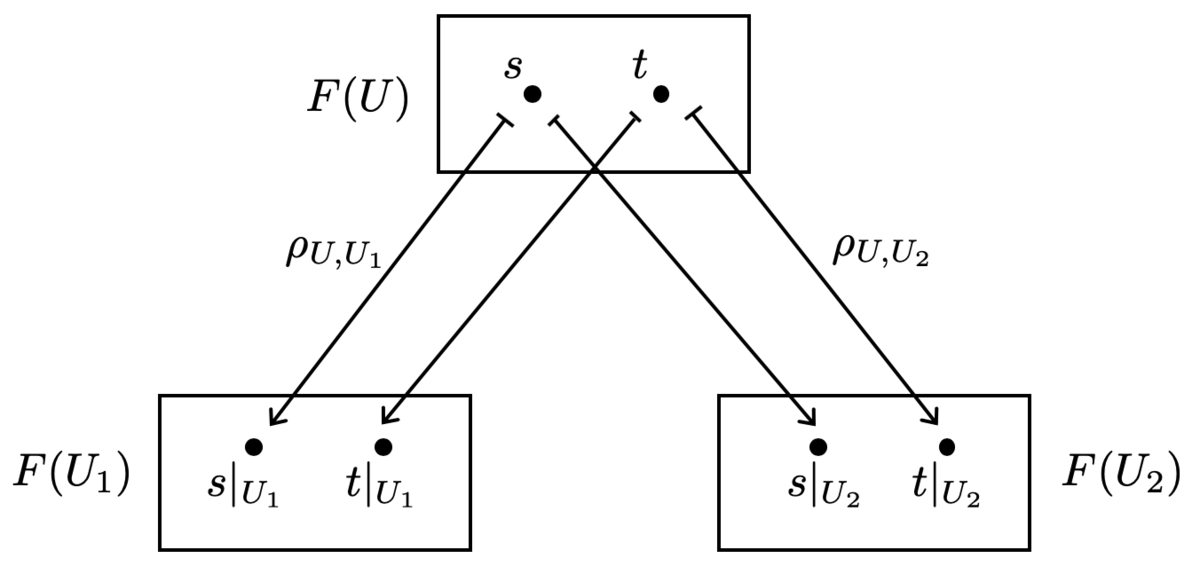
このとき、もしも かつ
ならば、元々の
も同じものだった、というのが既約性条件の主張です。
要するにこういうことですね。
つまり、開集合 上の関数
がイコールかどうかは、それを開被覆の各開集合上に制限したときにそれぞれでイコールかどうかで決まるっていうことですね。
今は、2つの制限写像を別々に考えていますが
というように と
をまとめた写像
を考えると
という条件とさらに言い換えることができます。
これはまさに、写像 の単射性そのものですね!
公理2:閉条件
もう一つの条件を確認しましょう。
をみたすものであるならば、常に の元
で
をすべての に対してみたすものが存在する。
これも同様に、現在の状況 に合わせて書き換えると、こうなります。
をみたすものであるならば、常に の元
で
をみたすものが存在する。
なるほど。
まず、 公理1と違う状況としては、開始地点が の組からスタートしていると言う点です。そして、
の組が
の条件を満たすのであれば、最終的には条件
を満たす
が得られるということを言っています。
公理1では からスタートしたので、ちょうど逆方向ですね。
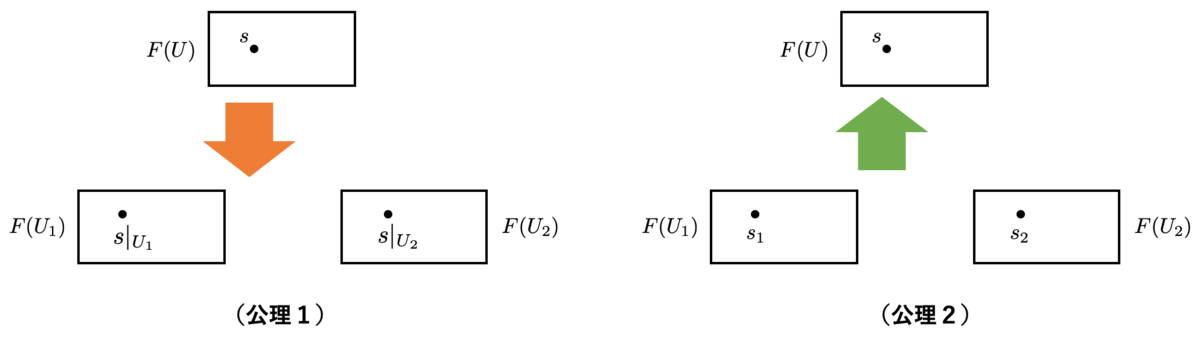
上の条件をもっと噛み砕くことを目指しましょう。まず、 の条件
ですが、1つ目の条件と4つ目の条件
は、明らかに常に満たされますから不要です。
残りの二つですが、 の役割を入れ替えても同値なので、本質的な条件は以下の1つだけであるとわかります。
これは、 と
を
の共通部分に制限したとき、つまり
上の切断
とみなしたときに、両者が一致するかどうかを聞いています。
ところで、仮定から でした。よって、
を考えることになります。
さて、 の元を
に制限させたとき、どのような元に写るのでしょうか。
実は、 が層であるならば、
となることが層の定義からわかります。これについては、補足1で詳しく議論することにしますので、ここでは事実だけ認めてしまいましょう。
結局のところ、この事実を認めれば、 は制限写像により
上でただ一つの元に写ります。よって
は常に成り立ちます。
以上から、実は に課せられた4条件は、
であれば、無条件で成り立つことがわかりました。
結局 としてはどのような組み合わせをとってもよいというわけですね。
よって、閉条件は以下のように大幅に簡単化されます。
をみたすものが存在する。
ここで言っていることは、切断の組 を勝手に決めると
が対応して、制限写像
で
に写るということです。
これはまさに、準同型写像 の全射性ですね!
例1のまとめ
一旦まとめましょう。
例1では、開被覆 として、
と
の間に共通部分を持たない場合を考えました。
このような場合には、2つの公理は次のようなわかりやすい主張に置き換えられるとわかりました。
- (公理1 既約性条件):準同型写像
の単射性を表す
- (公理2 閉条件):準同型写像
の全射性を表す
結局、アーベル群の間の準同型写像 は全単射より、
は同型写像です。よって
が成り立つことがわかりました。
我々が知りたかったのは だったわけですが、これが
の開被覆上の切断の直積によって書くことができるということですね。
たしかに、2つの条件は層の特徴的な性質を定めているといえそうです。
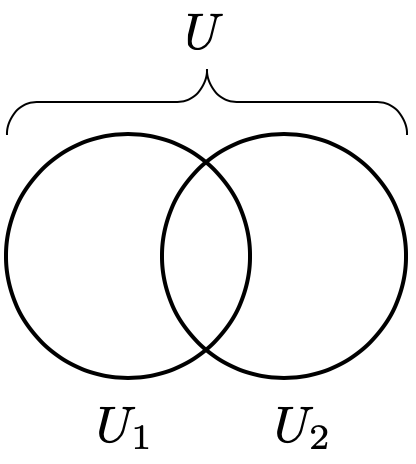
例2:共通部分を持つ開被覆
もう一つの例を考えましょう。今度は、開被覆 に対して、
と
に共通部分があるケースを考えます。図に表すと以下のような状況です。
以上の状況に対して、層の2つの公理を一つ一つ確かめていきましょう。
公理1:既約性条件
を満たすならば、常に が成立する。
これを、現在の状況 に合わせて書き換えると、こうなります。
を満たすならば、常に が成立する。
実は、既約性条件は例1のときと全く同じ結果になります。すなわち
なる写像を考えると
となるわけです。
まさに、 の単射性を表す条件ですね。
公理2:閉条件
もう一つの条件が、例1とは異なります。閉条件とは次の条件でした。
をみたすものであるならば、常に の元
で
をすべての に対してみたすものが存在する。
現在の状況 に合わせて書き換えると、こうなります。
をみたすものであるならば、常に の元
で
をみたすものが存在する。
ここで、例1のときと同様に
の中から不要な条件を取り除くと
となります。この条件は本質的で外すことができません。
これを踏まえて、再度、閉条件を言い換えるとこうなります。
をみたすものであるならば、常に の元
で
をみたすものが存在する。
さて、だいぶ簡単になってきましたが、この条件の意味するところは何なのでしょうか。
まず、 からそれぞれ
の組をとってきます。この
に対して、「ある条件」を満たすと
の元が定まるといっているわけです。その条件が、
であるということです。
条件 は何を言っているかというと、
の共通部分である
上での
の値が一致していないといけないということです。図で表すとこうでしょうか。

あっ、これ解析接続じゃん!!!
と思うわけです。解析接続との関係については、補足2で改めて言及します。
例1では全ての に対して
が対応する(全射)という話でしたが、例2のように共通部分を持つ場合には、必ずしも全射ではありません。共通部分
で一致するペアだけが
に対応することが許されるというわけです。
すなわち、 の部分集合
を考えると *1
は全射になるというわけですね。
まとめると、公理2は の像は、のりしろで「貼り合う」ような
の元全体
だけだよ、と言っていることがわかりました。
たとえば、 には
という2元しかなくて、
には
という2元しかなかったとしましょう。
もし
が成り立っているならば、 に対応する元
が
に存在することが言えます。
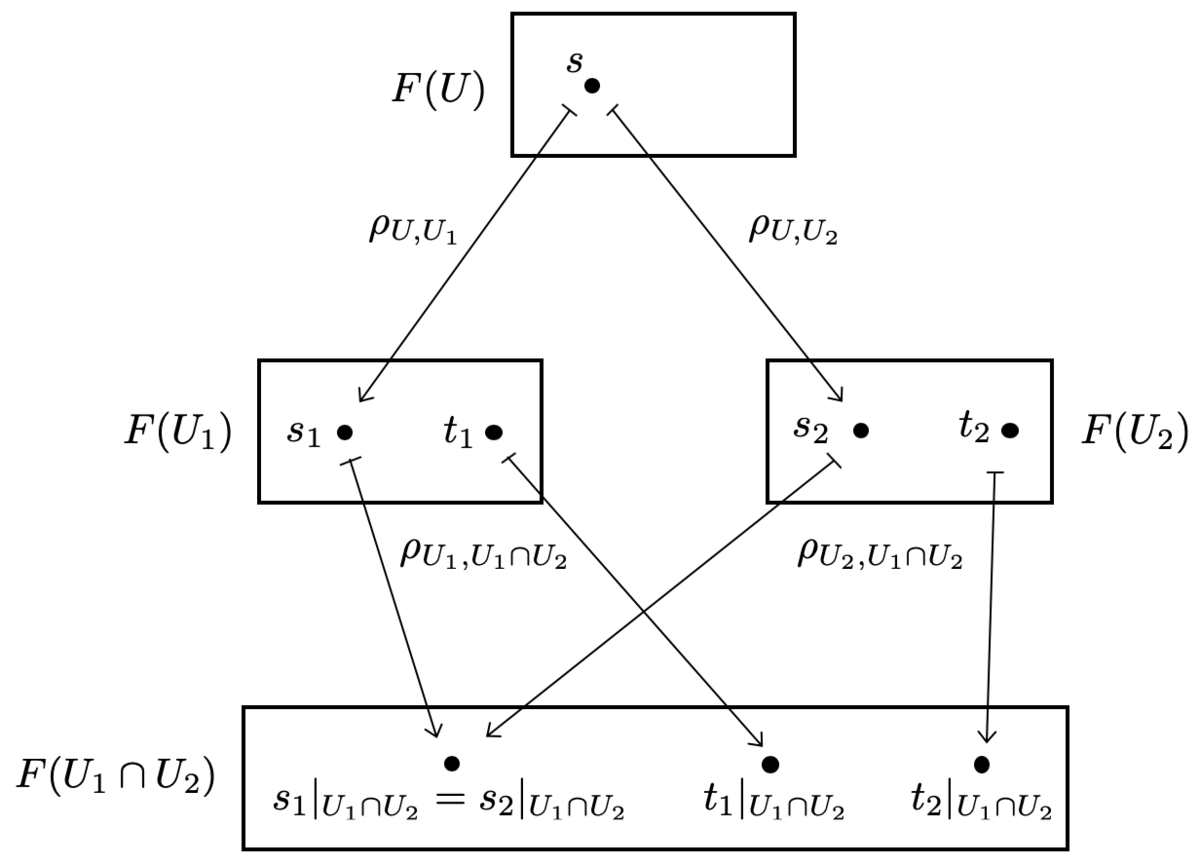
また、もし
が成り立っているならば、 に対応する元
が
に存在することが言えます。
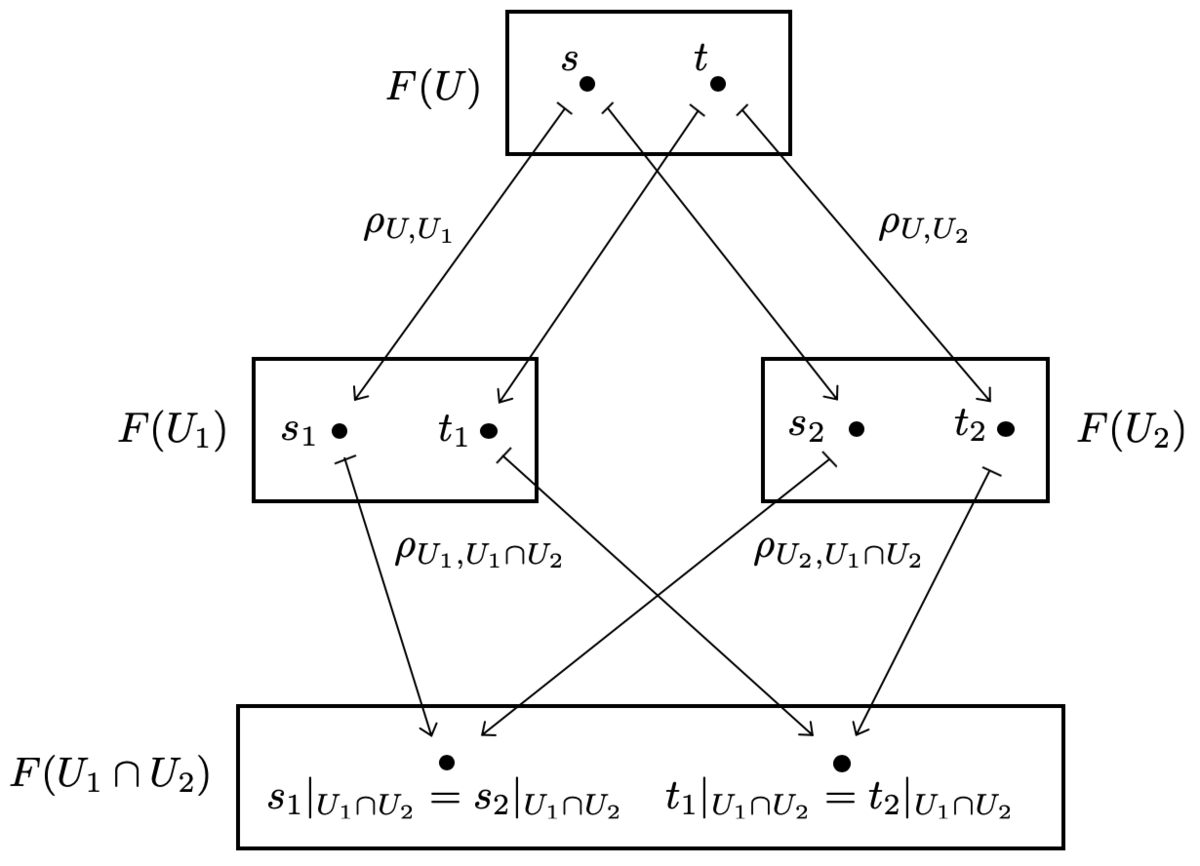
例2 まとめ
例2では、開被覆 として、
と
の間に共通部分を持つ場合を考えました。
このような場には、2つの公理は次のような主張に置き換えられることがわかりました。
- (公理1 既約性条件):準同型写像
の単射性を表す
- (公理2 閉条件):準同型写像
の像を定める(
は共通部分
で一致する
の部分集合
である)
これによりアーベル群の同型
が得られました。
完全列を用いた層の定義の言い換え
先ほどの例で分かったように、(公理1 既約性条件)は単射性を、(公理2 閉条件)は準同型写像の像を表しているのでした。
実は、このような条件は、完全列 を用いて言い換えることができます。
なる制限写像が与えられているとする。
の任意の開被覆
に対して以下の系列が完全列であるとき、
は
上の層という。
ただし、 は次の対応を与える準同型写像である。
前半はまったく同じなので、後半だけ見ましょう。
ただし、 は次の対応を与える準同型写像である。
上記の完全列が何を意味しているのかを、例2のケースに当てはめて考えてみましょう。
とすると
となります。
は具体的に
と表せます。
簡単のため完全列を2つに分けて考えましょう。まずは前半の完全列
ですが、これは は単射である ということを表しています。
は
でしたから、まさに公理1の条件そのものですね!
次に、後半の完全列
を考えます。完全性より
が成り立ちます。我々が知りたいのは ですから、
を計算すればよいですね。
は
でしたから、 は右辺の組の要素がすべて 0 になる
全体ということになります。すなわち
ということですが、これはまさに公理2そのものですね。
これらのことは、 を任意の開被覆としても成り立ちます。
というわけで、上の完全列の前半が(公理1 既約性条件)を、後半が(公理2 閉条件)を表していることがわかりました。

完全列に表したことで見た目的にもすっきりして気持ちいいですが、単に見た目の問題だけでなく、より発展的な意味合いもあります。
完全列で表すことにより、層の定義の大部分を圏論の言葉で表すことができました。あとは開被覆 と共通部分
だけが具体的な表現に依存しています。
については、ファイバー積によって表すことができるので、残りは開被覆だけです。
そこで、 が必ずしも包含写像でない場合にも「射の族
が(何がしかの意味で)被覆である」という条件が与えられれば、同じように層の理論を組み立てることができます。一般化できるわけですね。
また、対象をスキームとして、射をエタール射に置き換えた圏を考えると、その上でエタール層と呼ばれる層の類似物を定義することができます。このエタール層の層係数コホモロジーこそが、あの有名なエタール・コホモロジーです。そう言われるとちょっと嬉しく感じてきますよね。
tsujimotterがスキームや層を勉強している動機の一つは、このエタール・コホモロジーの理解にあります。今回こうして層の定義を理解できたことで、 ぐらいは目標に近づいたのではないかなと感じています。
まとめ
まとめると、層の定義における2つの公理は、次のような主張であることがわかりました。
- (公理1 既約性条件):準同型写像
の単射性を表す
- (公理2 閉条件):準同型写像
の像
を定める
また、完全列によって、圏論的な言葉を用いて層を定義できることについても触れました。
上の結果を鑑みるに、層とは
大域的な構造
というなのでしょう。局所的なところだけ見れば、全体がわかってしまう、そういった統制の取れた性質を持つ関手を層というのでしょうね。
そういえば、ハーツホーンには次のような記述があったことを思い出しました。
層とはおおざっぱにいうと,その切断が局所的な情報によって定まる前層である.
まさに私が今言ったようなことですね。
このことに気づいて、なるほどな、層ってそういうことだったのか、と思いました。(ダジャレではなく、実際にそう思いました)
それでは今日はこの辺で。
補足1:U = ∅ の場合
特殊なケースとして、 を考えてみましょう。このとき、
であることについて説明します。
実は、ハーツホーンにおける層の定義では、前層の定義の時点で を仮定しています。一方で、層の2つの公理から
を導けるということを、p進大好きbotさんという方に教えていただきました。そこで補足1では、p進大好きbotさんに教えていただいた内容を元に、私なりに理解した部分を再構成してまとめたいと思います。
まず、 の開被覆を考えます。
一般に空集合に限らない開集合 の開被覆とは、添字集合
から
への写像
で、その和集合が
となるものをいいます。
ここで、添字集合として を考えましょう(ここがポイントです!)。このとき
は空集合からの写像(つまり、空写像)となります。ここで和集合
を考えたいのですが、この定義は
でした。 なので、右辺は空集合
になります。よって、
は
の開被覆を定めます。
次に、アーベル群の直積 について考えます。
として
と定義されます。
ここで のとき、条件
は恒真となります。したがって、任意の
が直積の要素となるはずです。
一方、空集合からの写像は空写像ただ一つなので、これを と表記すると、結局
となります。これは単位元 をただ1つ持つアーベル群です。
以上で準備は整いました。上記の考察により、層の完全列は
となります。したがって完全性より
が得られると言うわけです。
補足2:解析接続と閉条件
例2の計算をしている途中でも触れましたが、層の公理と解析接続の間には関係があります。
位相空間 として、複素数平面
を考えます。
の開集合
に対して、
上で正則な複素関数全体を
とすることにします。このような
は、通常の意味での制限写像を考えることで前層になることはただちにわかります。さらに言えば、
は層にもなっています。そのことを確かめましょう。
点 のまわりで正則な関数
を
を中心にテイラー展開します:
収束半径を として、収束円の内側を
としましょう。
また、点 のまわりで正則な関数
を
を中心にテイラー展開します:
収束半径を として、収束円の内側を
としましょう。
ここで、 と
の間には共通部分
があり、
上の連結成分上で
と
が同じ値をとるとしましょう。

このとき、 は
に 解析接続 するといいます。要するに、
上で
をとり、
上で
をとるようなものをセットで「関数」だと思えば、
全体で正則な複素関数
が作れるわけですね。
これを層の言葉で言い換えるとこうなります。 は
の開被覆を定めます。
が共通部分
で同じ値をとるとき、
全体で正則な複素関数
が存在することが公理2の要請から言えます。この
とは、
に制限すると
に、
では
にそれぞれ一致する関数です。
さらに、このようにできた関数 が一意に定まるというのが複素関数論における 一致の定理 でした。すなわち、これは公理1の主張そのものです。
つまり、解析接続を表しているのが公理2で、その解析接続された関数の一意性を主張するのが公理1だったということですね。
あぁ、層の定義と複素関数論がようやくつながりました。よかった。
参考文献
層の定義はこちらを参考にしていますが、一部記述を変えています。
前層や圏論周りの定義の確認などはこちらを参考にしました。

- 作者:Tom Leinster
- 出版社/メーカー: 丸善出版
- 発売日: 2017/01/29
- メディア: 単行本(ソフトカバー)
補足1の直積の定義などについては、集合・位相入門などで確認しました。
圏論化することによる層の一般化の話は、整数論サマースクールの三枝先生の記事で読みました。この記事を理解できるようになることが、私の目標の一つです。
http://www4.math.sci.osaka-u.ac.jp/~ochiai/ss2009proceeding/SummerSchool-0201-2.pdf
*1:この という記号は、本ブログ独自の記号であり、他で使われるものではありません。

