日曜化学(2.5)：メトロポリス・ヘイスティングス法を用いた電子雲の可視化（Python/matplotlib）

前回の記事で、水素原子の電子雲の可視化する方法として、３つの方法を紹介しました。
tsujimotter.hatenablog.com

特に、方法２「散布図としてプロット」については、棄却サンプリング法を使った方法を紹介しました。

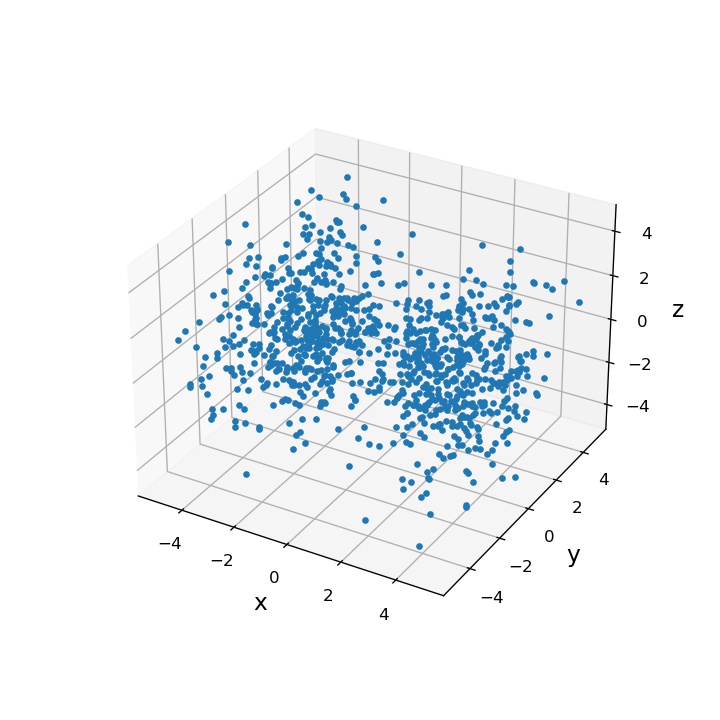
散布図としてプロットするにあたって、電子の確率分布を表す（3次元の）確率密度関数 $f(x, y, z) = |\Psi(x, y, z)|^2$ にしたがう乱数を得る必要がありました。

棄却サンプリング法は、 $f(x, y, z)$ とは直接関係ない（たとえば一様乱数のような）確率分布 $g(x, y, z)$ にしたがう乱数から、 $f$ と $g$ の確率密度関数としての差を考慮しつつ、適切な確率で乱数を「棄却」することによって、目的の $f(x, y, z)$ にしたがう乱数を得る手法です。

ところがこの方法、非常に時間がかかることが知られています。実際、上記の散布図を描くだけでかなりの時間を要しました。特に、 $f$ と $g$ の差が大きければ大きいほど、棄却率が高くなり、乱数を生成するのに時間がかかるというわけです。

今回紹介するメトロポリス・ヘイスティングス法を用いれば、上記の問題の多くは解決します。

マルコフ連鎖モンテカルロ法（MCMC）という一般的な枠組みの一手法であり、棄却サンプリングのような素朴な手法と比べて、効率的に乱数生成を行うことができます。

これまでこの手の手法（マルコフ連鎖モンテカルロ法）については、話には聞いてはいたものの、なんとなく手が出せないでいました。しかしながら、今回の目的に向けて調べてみると、案外簡単に実装できることがわかりました。（やっぱりモチベーションって大事ですね。）

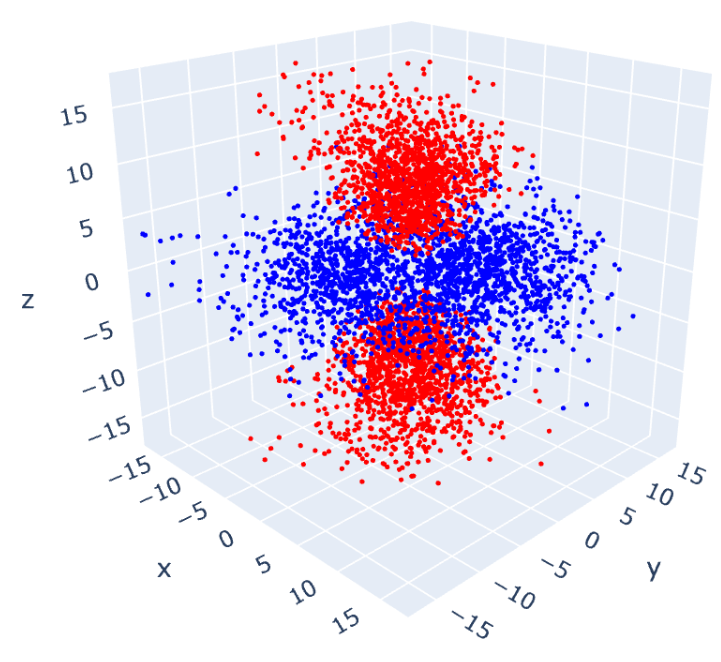
仕組みはちゃんと理解できているわけではないですが、アルゴリズムの流れと実装方法は理解できたので、電子雲の可視化に応用してみたというのが今回の記事です。

当初の予定では、日曜化学シリーズの記事として書く予定はなかったので、番外編として日曜化学(2.5)としています。よろしければご覧になってください！

メトロポリス・ヘイスティングス法

簡単にアルゴリズムの流れを紹介します。

このアルゴリズムによって生成したいのは、波動関数を $\Psi(x, y, z)$ として、確率密度関数 $P(x, y, z) = |\Psi(x, y, z)|^2$ にしたがう $N$ 個のランダムな3次元ベクトルの列

${\bf x}_1, \; {\bf x}_2, \; {\bf x}_3, \; \ldots, \; {\bf x}_N$

です。

まず、3次元ベクトル ${\bf x} = (x, y, z)$ および ${\bf u} = (u, v, w)$ を変数に持つ、条件付き確率密度関数 $Q({\bf x} \mid {\bf u})$ を用意します。この $Q$ を提案分布といいます。

この $Q$ については、 ${\bf u}$ に対して $Q({\bf x} \mid {\bf u})$ にしたがうランダムなベクトル ${\bf x}$ を生成できるような関数（乱数が作れる確率密度関数）に決める必要があります。また、あとに示す「条件」を満たすようにすると話が簡単になります。

初期値となる3次元ベクトル ${\bf x}_0 = (x_0, y_0, z_0)$ を用意します。

${\bf x}_0$ からスタートし、 ${\bf x}_0$ の情報から ${\bf x}_{1}$ を生成します。続けて ${\bf x}_1$ の情報から ${\bf x}_{2}$ を生成します。こんな風に ${\bf x}_t$ の情報から ${\bf x}_{t+1}$ を生成するというのを $t = 0, 1, 2, \ldots, N-1$ に対して行います。
（時刻 $t$ の情報に基づいて、時刻 $t+1$ における状態の確率が定まる系のことを「マルコフ連鎖」といいます。）

より具体的な生成方法として、先ほど用意した $Q$ を用いて、 $Q({\bf x}_{t+1}^* \mid {\bf x}_{t+1})$ によって、 ${\bf x}_{t+1}$ の候補となる乱数 ${\bf x}_{t+1}^*$ を生成します。以下の確率 $\alpha$ によって、候補 ${\bf x}_{t+1}^*$ を ${\bf x}_{t+1}$ として採用します。

$\displaystyle \alpha = \frac{P({\bf x}_{t+1}^*) \cdot Q({\bf x}_{t} \mid {\bf x}_{t+1}^*)}{P({\bf x}_{t}) \cdot Q({\bf x}_{t+1}^* \mid {\bf x}_{t})} \tag{1}$

ただし、 $\alpha > 1$ のときは、 $\alpha = 1$ とします。

逆に、確率 $1-\alpha$ によって、 ${\bf x}_{t+1}^*$ を棄却します。この場合、再度同じ手順で ${\bf x}_{t+1}^*$ を得て、同様に上記の確率で採用するか棄却するかを判定します。

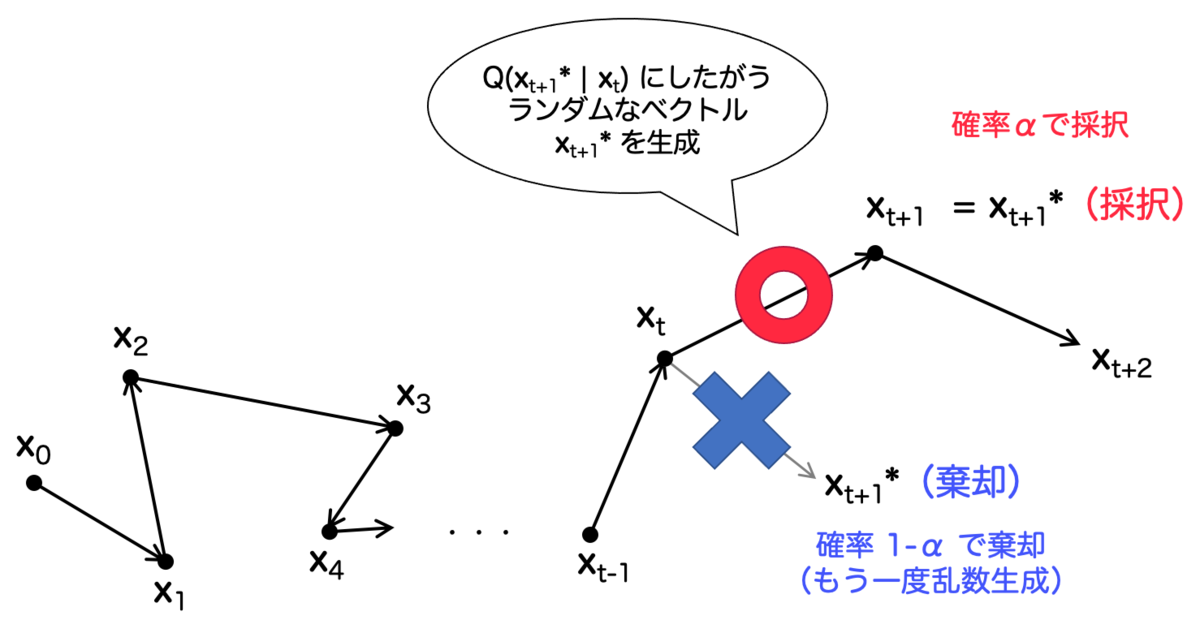
以上を繰り返して、採用されたランダムなベクトルの列

${\bf x}_1, \; {\bf x}_2, \; {\bf x}_3, \; \ldots, \; {\bf x}_N$

を考えると、これが目的の分布 $P(x, y, z)$ にしたがうランダムなベクトルの列となっているというわけです。

たったこれだけなので、実装も非常に簡単です。理屈を理解していないので、こんな方法でなぜうまくいくのかはよく分かりませんが、とにかくこれでうまくいくのだそうです。

また、 $Q({\bf x} \mid {\bf u})$ を決める必要がありますが、これについては多次元正規分布を用いることにします。

$\displaystyle Q({\bf x} \mid {\bf u}) = \frac{\exp\left( -\frac{1}{2}({\bf x} - {\bf u})^T \Sigma^{-1}({\bf x} - {\bf u}) \right)}{\sqrt{(2\pi)^k |\Sigma|}} \tag{2}$

ここで、 $\Sigma$ は分散共分散行列です。変数間の相関を考える必要がないので、単に対角行列を考えれば十分です。

この $Q$ は「① $Q({\bf x}_{t+1}^* \mid {\bf x}_{t+1})$ にしたがうランダムなベクトル ${\bf x}_{t+1}^*$ を生成する」と「② 式 $(1)$ を計算するのに用いる」という２つの役割があります。

①については、numpyに多次元正規分布にしたがう乱数を生成する関数

np.random.multivariate_normal

がありますので、これを使えば簡単です。具体的な使い方は、こちらのページを参照。

②については、そもそも計算する必要がないという話があります。というのも、式 $(2)$ の形を見ると、明らかに ${\bf x}$ と ${\bf u}$ で対称的な形になっていますね。すなわち

$Q({\bf u} \mid {\bf x}) = Q({\bf x} \mid {\bf u}) \tag{3}$

ということです。

この性質を使うと、式 $(1)$ は次のように劇的に簡単になります：

$\require{cancel} \displaystyle \alpha = \frac{P({\bf x}_{t+1}^*) \cdot \cancel{Q({\bf x}_{t} \mid {\bf x}_{t+1}^*)}}{P({\bf x}_{t}) \cdot \cancel{Q({\bf x}_{t+1}^* \mid {\bf x}_{t}})} = \frac{P({\bf x}_{t+1}^*)}{P({\bf x}_{t})} \tag{4}$

なるほど、これなら $Q$ の値は計算する必要がなくなりますね。むしろこうなるように、多次元正規分布を選んだということでしょう。

さらにいうと、棄却率を計算する $P({\bf x}_{t+1}^*)$ と $P({\bf x}_{t})$ という式は、その比がわかれば十分です。つまり、波動関数の規格化定数はわからなくても全く問題ないのです。波動関数の規格化定数の決定は大変面倒だったので、この性質はありがたいですね。

電子雲を可視化するPythonプログラム

そんなわけで、メトロポリス・ヘイスティングス法を用いた可視化のプログラムを紹介します。

例によってPythonのmatplotlibを使っていますので、以下をインストールしておいてください。

numpy
matplotlib

また、前回紹介したPlotlyというライブラリを使った可視化もできるようになっています。使いたい人は、Plotlyをインストールした上で、適切にコード内のコメントアウトを外してください。

# メトロポリス・ヘイスティング法による電子分布の可視化

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d.axes3d as axes3d

import math


# 動径波動関数（ボーア半径を a_0 = 1 に正規化）
def radial_wave_function(r, n, l, Z_eff):
    rho = 2.0 * Z_eff * r / n
    if n == 1 and l == 0:
        return (Z_eff ** 1.5) * np.exp(-rho/2.0) * 2.0
    elif n == 2 and l == 0:
        return (Z_eff ** 1.5) * np.exp(-rho/2.0) * (2.0 - rho) / (2.0*np.sqrt(2.0))
    elif n == 2 and l == 1:
        return (Z_eff ** 1.5) * np.exp(-rho/2.0) * rho / (2.0*np.sqrt(6.0))
    elif n == 3 and l == 0:
        return (Z_eff ** 1.5) * np.exp(-rho/2.0) * (6.0 - 6.0*rho + rho**2) / (9.0*np.sqrt(3.0))
    elif n == 3 and l == 1:
        return (Z_eff ** 1.5) * np.exp(-rho/2.0) * (4.0 - rho) * rho / (9.0*np.sqrt(6.0))
    elif n == 3 and l == 2:
        return (Z_eff ** 1.5) * np.exp(-rho/2.0) * (rho**2) / (9.0*np.sqrt(30.0))


# 球面調和関数（ただし、実関数表示したもの）
def spherical_harmonics(theta, phi, l, m):
    if l == 0:
        if m == 0:
            # l=0, m=0
            return np.sqrt(1.0/(4*np.pi))
    if l == 1:
        if m == 0:
            # l=1, m=0
            return np.sqrt(3.0/(4.0*np.pi)) * np.cos(theta)
        if m == 1:
            # l=1, m=+1
            return np.sqrt(3.0/(4.0*np.pi)) * np.sin(theta) * np.cos(phi)
        if m == -1:
            # l=1, m=+1
            return np.sqrt(3.0/(4.0*np.pi)) * np.sin(theta) * np.sin(phi)
    if l == 2:
        if m == 0:
            return np.sqrt(5.0/(16.0*np.pi)) * (3.0*(np.cos(theta)**2) - 1.0)
        if m == 1:
            return np.sqrt(15.0/(4.0*np.pi)) * np.cos(theta) * np.sin(theta) * np.cos(phi)
        if m == -1:
            return np.sqrt(15.0/(4.0*np.pi)) * np.cos(theta) * np.sin(theta) * np.sin(phi)
        if m == 2:
            return np.sqrt(15.0/(16.0*np.pi)) * (np.sin(theta)**2) * np.cos(2*phi)
        if m == -2:
            return np.sqrt(15.0/(16.0*np.pi)) * (np.sin(theta)**2) * np.sin(2*phi)

        
        
# 水素様原子の波動関数 Ψ_{n,l,m}(x, y, z)
#
# (n,l,m): 量子数
# Z_eff:   有効核電荷
# 
def f(x, y, z, n, l, m, Z_eff):
    # 座標系を (x,y,z) -> (r,θ,φ) に変換
    r = np.sqrt(x*x + y*y + z*z)
    
    theta = 0.0
    phi = 0.0
    if r > 0:
        theta = np.arccos( z / r )
    if y == 0:
        if x < 0:
            phi = np.pi
    elif x*x+y*y > 0:
        phi = np.sign(y) * np.arccos(x/np.sqrt(x*x+y*y))
        
    # 動径波動関数と球面調和関数の積を計算して出力
    return (radial_wave_function(r, n, l, Z_eff) * spherical_harmonics(theta, phi, l, m))


# 量子数
n = 3
l = 2
m = 0

# 有効核電荷
Z = 1        # 水素原子を想定しているので Z = 1
Z_eff = Z


# サンプリング数の設定
N = 5000                  # サンプリング目標個数
x_range = 18              # 座標の範囲 (-x_range, x_range)


# メトロポリス・ヘイスティング法を使った電子雲のサンプリング
num_of_points = 0  # 採択されたデータ数

x = 1
y = 1
z = 1


# 波動関数が正のデータを格納する変数
x1_list = []
y1_list = []
z1_list = []

# 波動関数が負のデータを格納する変数
x2_list = []
y2_list = []
z2_list = []



while num_of_points < N:
    if num_of_points % 10 == 0:
        print(num_of_points)
    # 確率分布 Q(x*|x_t) から次の状態の候補 x* の乱数生成（今回は Q として3次元ガウス分布を選択）
    values = np.random.multivariate_normal([x, y, z], [[10,0,0],[0,10,0],[0,0,10]], 1)  # 乱数生成
    x_star = values[0,0]
    y_star = values[0,1]
    z_star = values[0,2]

    f_t = f(x, y, z, n, l, m, Z_eff)                    # xの波動関数
    f_star = f(x_star, y_star, z_star, n, l, m, Z_eff)  # x* の波動関数

    # 採択率を計算  α = p(x*) / p(x_t)
    alpha = (f_star ** 2) / (f_t ** 2)

    # 採択率により決定
    r = np.random.rand(1)[0]   # 0 <= r <= 1 の一様乱数 r を生成
    if r <= alpha:
        x = x_star
        y = y_star
        z = z_star
        if f_star > 0:
            x1_list.append(x)
            y1_list.append(y)
            z1_list.append(z)
        else:
            x2_list.append(x)
            y2_list.append(y)
            z2_list.append(z)            
        num_of_points += 1



# figureを生成する
X1 = np.array(x1_list)
Y1 = np.array(y1_list)
Z1 = np.array(z1_list)

X2 = np.array(x2_list)
Y2 = np.array(y2_list)
Z2 = np.array(z2_list)



# matplotlibによる可視化
fig = plt.figure(figsize=(8.0, 8.0))
ax = fig.add_subplot(1,1,1, projection='3d')

ax.set_xlim3d(-x_range, x_range)
ax.set_ylim3d(-x_range, x_range)
ax.set_zlim3d(-x_range, x_range)

# 軸の設定
ax.set_xlabel("x", size = 14)
ax.set_ylabel("y", size = 14)
ax.set_zlabel("z", size = 14)

ax.plot(X2,Y2,Z2,color='b',marker=".",linestyle='None')
ax.plot(X1,Y1,Z1,color='r',marker=".",linestyle='None')

plt.show()


'''
# Plotlyによる可視化
import plotly.graph_objects as go

fig = go.Figure(data=[go.Scatter3d(
    x = X1,
    y = Y1,
    z = Z1,
    mode='markers',
    marker = dict(
        size = 1,
        color = 'red'
    )
), go.Scatter3d(
    x = X2,
    y = Y2,
    z = Z2,
    mode='markers',
    marker = dict(
        size = 1,
        color = 'blue'
    )
)])

fig.update_layout(
    scene = dict(
        camera=dict(eye=dict(x=1.7, y=-1.7, z=1.7)),  #eye=dict(x=1.25, y=1.25, z=1.25)), 
        xaxis = dict(range=[-x_range, x_range]),
        yaxis = dict(range=[-x_range, x_range]),
        zaxis = dict(range=[-x_range, x_range]),
        aspectmode='cube', #this string can be 'data', 'cube', 'auto', 'manual'
        #a custom aspectratio is defined as follows:
        aspectratio=dict(x=1, y=1, z=0.95)
    ),
    width=700,
    height=700,
)

fig.show()
'''

上記のコードは、量子数 $(n, l, m) = (3, 2, 0)$ に対応する水素原子の波動関数（すなわち、d軌道）を図示するものです。量子数については、以下の部分を変更すれば、違うものをプロットすることができます。

# 量子数
n = 3
l = 2
m = 0

また、デフォルトではサンプル数5000としていますが、これも変更可能です。

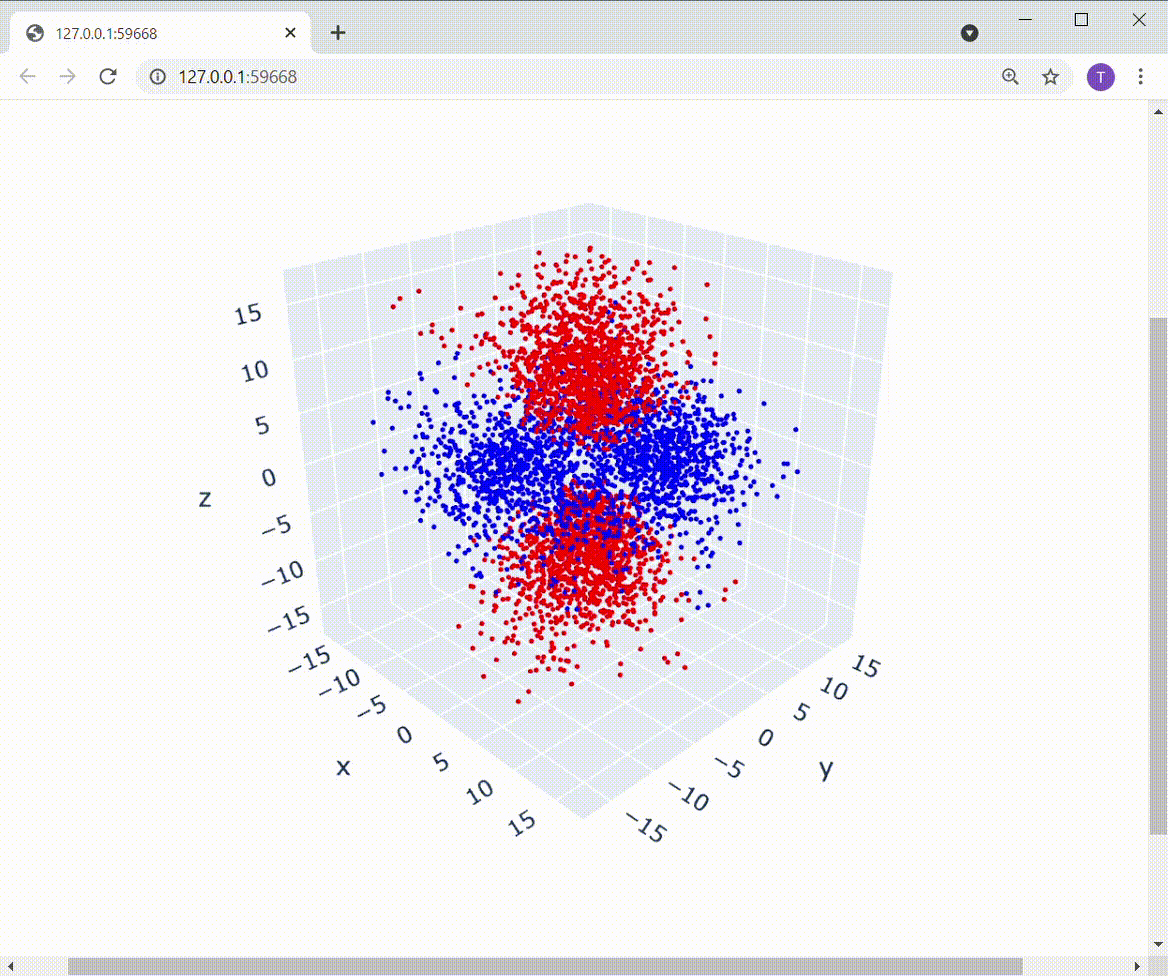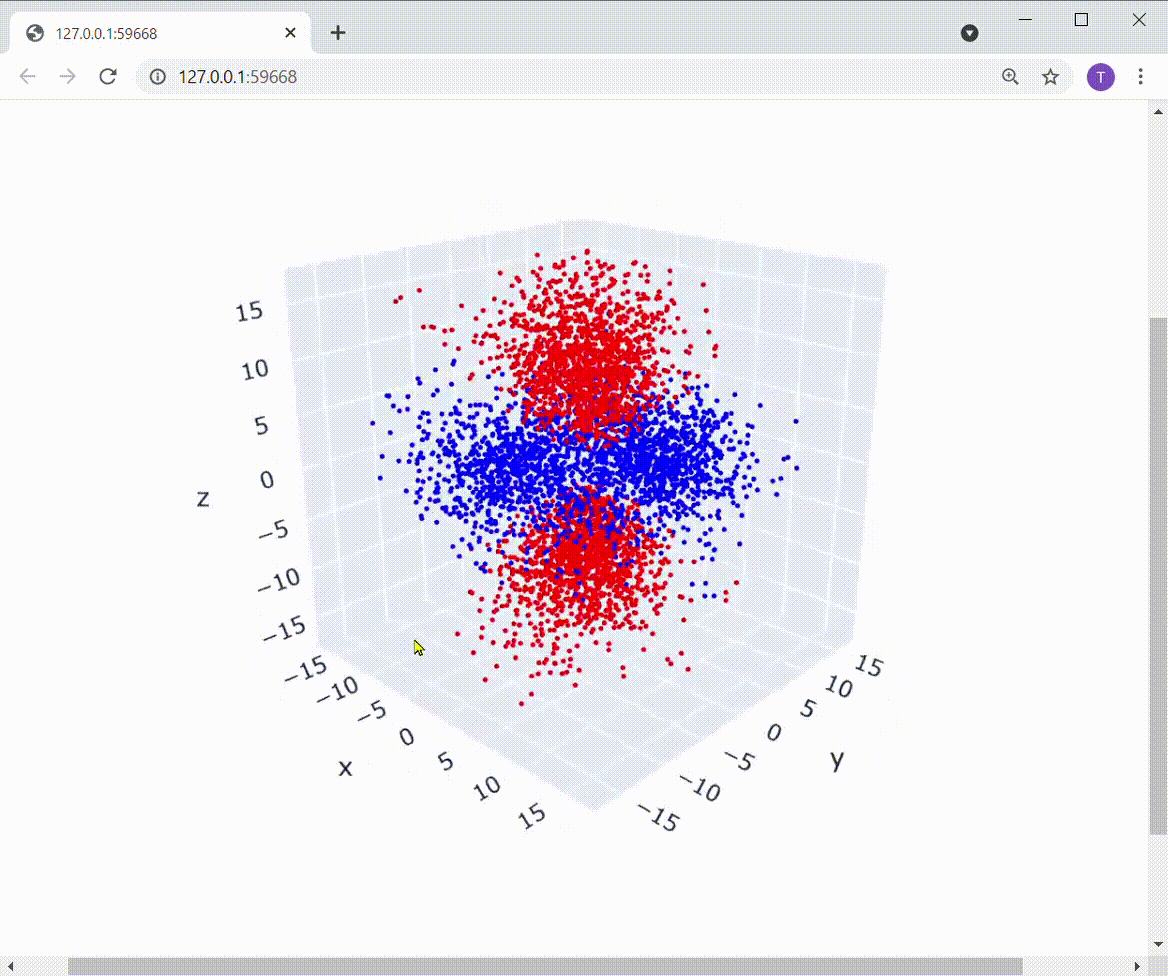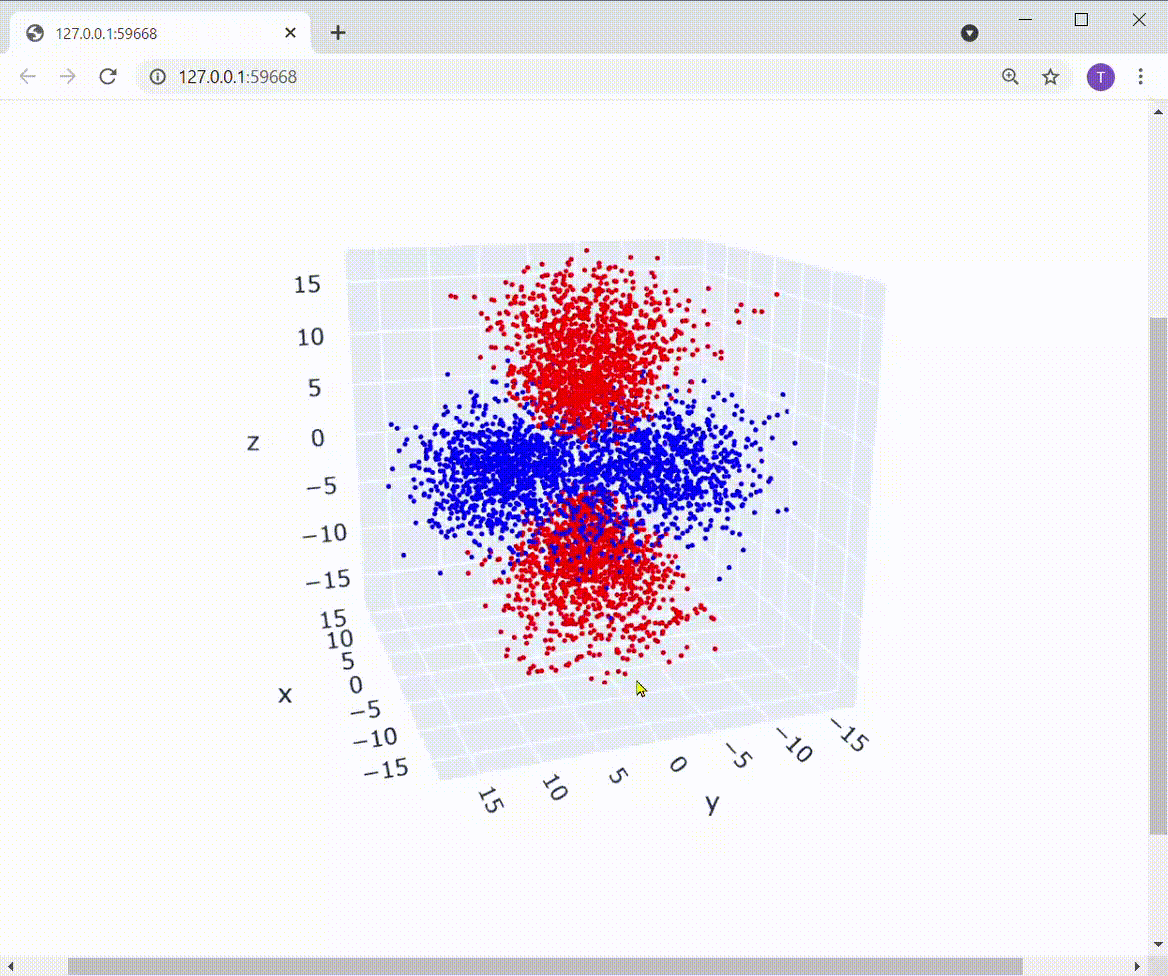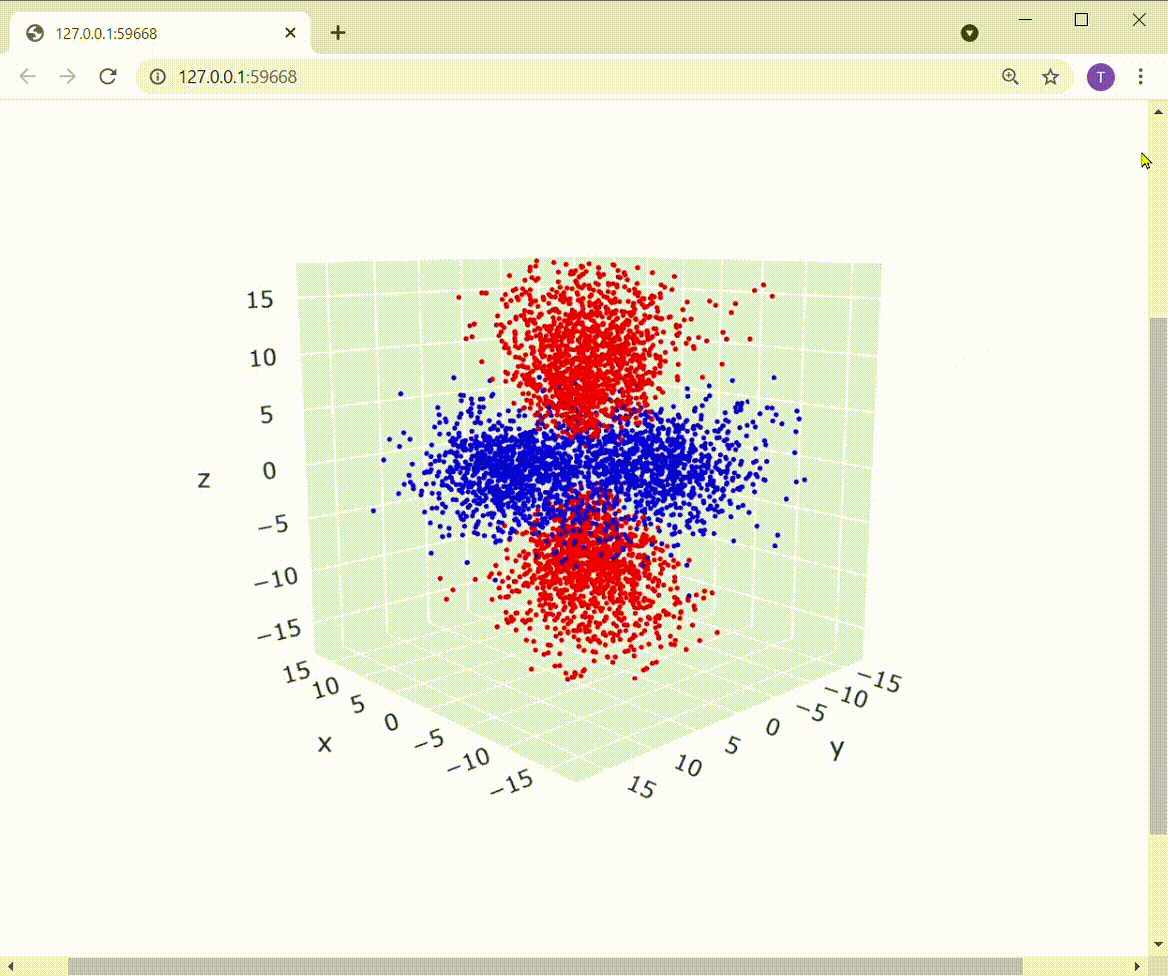
実行してみると、冒頭に紹介した以下の図が得られます。

図はPlotlyによるもの

たしかにd軌道の形に電子が分布していますね！！すごい！！

実際実行してみると分かりますが、5000個のサンプリングであっても、ものの数秒で実行完了します。これは棄却サンプリングの結果とは大違いです。

超楽しい！！！

次回の記事はこちら

tsujimotter.hatenablog.com

参考にしたページ

追記：2021.07.12

@dc1394さんという方が開発されている「SchracVisualize_Direct3D_11」をご紹介させてください。水素原子の可視化ツールです。実行ファイルによりローカルで実行でき、とても高速に、綺麗な絵を出力してくれます。（3次元をマウスでグリグリ動かして見ることができて便利です。）

「SchracVisualize_Direct3D_11」がv0.3にバージョンアップしました！
アルゴリズムの変更（棄却法をメトロポリス・ヘイスティングス法に）により、描画が高速になっています。バイナリは以下URLからダウンロードできます。左図は水素原子の5dxy軌道、右図は5fxz^2軌道です。https://t.co/yyJWi9Sb3H pic.twitter.com/dWkuKHaFJs
— dc1394 (@dc1394) 2021年7月12日