いよいよ 分子軌道 を計算してみたいと思います。
今回の記事の内容を理解するとエチレンやブタジエンやベンゼンなどの分子軌道が計算でき、それをPythonのプログラムで可視化できるようになります。

過去の記事を前提にお話しますので、まだの方はシリーズの過去記事をご覧になってください。
tsujimotter.hatenablog.com
(番外編の日曜化学(2.5)は読まなくても、今回の内容については大丈夫です。)
前回までの記事で計算したのは、水素様原子という 原子核が1つ・電子が1つ のものでした。
そうなると、原子核が2つ以上で電子が1つ の状況(つまり分子)を計算したくなると思います。

上記の状況はポテンシャルによって表すことができますので、ハミルトニアンに反映させればシュレーディンガー方程式を立式すること自体は可能です。(これはあとでやりたいと思います。)
ところがどっこい、この状況のシュレーディンガー方程式を解こうと思うと、もはや厳密には解けなくなってしまうのです。
ここで「量子力学はこんなものなのか」とがっかりしないでください。近似的にであれば、実用的には十分解くことができるというのが今回のお話です。
そのための方法が 分子軌道法 です。
今回の記事では、分子軌道法の基本的な原理の紹介と、エチレンやベンゼンなどのいくつかの分子について、電子軌道を可視化してみたいと思います!
これまで通り、可視化に用いたPythonプログラムも紹介するので、ぜひ遊んでみてください。とても楽しいです!
目次:
実はこの話、私が大学1年に入った頃に習った内容なのですが、当時はさっぱりわからなかったのを記憶しています。なんとなくよくわからない前提を紹介されて、そこから突然「安定性軌道」とか「反安定性軌道」といった、分子軌道法の様々な概念が紹介されていきました。私はいったい何に立脚して考えれば良いのか、よくわかりませんでした。
それもそのはず、本当は量子力学を知らないといけなかったのです。量子力学の基本的なことを勉強したあとで改めて読んでみると「なんだこんなことだったのか」と。
やっぱり基本的な前提があやふやな状態では、理解にはたどり着けないということですね。
ここまで読んできた方であれば十分ついていける内容です。かなりの長文記事ですが、丁寧な解説を心掛けたつもりですので、よろしければ最後まで読んでいただければ幸いです。
1. 分子軌道法の考え方(概要)
まずは大まかに分子軌道法の考え方について紹介します。
最終的な目標は、2つ以上の原子核で構成された分子に属する電子を考えて、その真の波動関数 を求めることです。
このために分子の状況を表すハミルトニアン を考えます。ハミルトニアン
に対応するシュレーディンガー方程式
を立式できて、これは固有値問題になっています。これを解くことができれば、分子内の電子が取りうる真のエネルギー が求まり、対応する真の波動関数
が得られるはずです。
ところがです。このような状況のシュレーディンガー方程式は、複雑すぎて厳密には解けないことが知られています。さぁ困った!!
ここで必要になるのは、解ける問題にどうにかして帰着できないか という考え方です。我々が解くことができるのは、水素様原子(原子核1個・電子1個)の場合だけです。
たとえば2つの原子核の状況を考えて、原子核2がとーっても遠い位置にあるという状況を考えましょう。

このような状況では、電子にとっての状況は、原子核1の周りだけを回っているのとそう変わりません。つまり、原子核1についての、水素様原子の解を考えればよいわけです。電子が原子核2の周囲にいる場合も同様です。
そんなわけで、 が十分大きい場合においては、原子核1の周りでは電子が(原子核1についての)水素様原子の波動関数
に近似でき、原子核2の周りでは同じく(原子核2についての)水素様原子の波動関数
に近似できそうです。

もちろん、 が小さい場合にはそうはいきません。しかしながら、そうはいっても上記の状況と大きく変わることはないだろうという「仮定」を置くのです。なかなか大胆な仮定ですね。
ここで、二つの既知の波動関数 の線形結合
を考えます。波動関数の線形結合のことを量子力学では 「重ね合わせ」 と呼びますが、文字通り電子の波が重なっているようなイメージです。
分子における真の波動関数 は、このような重ね合わせによって近似できると考えるのです。もう少し正確にいえば、真の波動関数の近似
になるような を探す問題だと捉えなおすわけです! 見事な発想の転換ですね!!
ここで 「変分原理」 と呼ばれる性質を活用します。 に対応する波動関数
のエネルギーを
とすると、真のエネルギー
に対して常に
が成り立つというものです。
したがって、エネルギー が最小になるような
を求めれば、それが真のエネルギーの近似値になっていると考えることができそうです! このようにして得られた軌道を 「分子軌道」 といいます。
このような方法により近似的に分子軌道を求める手法を、量子力学では 「変分法」 と呼ぶそうです。
以上が分子軌道法のアイデアです。いやー、アイデアだけでもめちゃめちゃ面白いですね!!
分子軌道法を具体的に理解するためには、まずは「重ね合わせの原理」について理解する必要があります。重ね合わせの原理と、重ね合わせの状況におけるエネルギーの計算方法について、次節で説明してから分子軌道法の具体的な計算にいきたいと思います。
2. 重ね合わせの原理
量子力学においては、電子などのミクロな粒子は「異なる量子状態の重ね合わせ」として存在するのだという話を聞いたことがある人はいるかと思います。
第1回の記事から紹介しているシュレーディンガー方程式を考えます。
この方程式は、ハミルトニアン についての固有値
に対する固有方程式になっていることは以前話しました。固有値に対応して固有空間が定まり、
はその空間の元であるということでした。
2つの固有値 に対応する解として波動関数
と
を考えます。これらの線形結合を
とすると、 は
という状態と
という状態が「重なり合った状態」であると考えられます。この重ね合わせもまたシュレーディンガー方程式
の解であり、電子の取りうる状態なのです。
・・・といいたいところなのですが、これはそもそもシュレーディンガー方程式 の解にはなっていません。つまり、グレーの部分が間違いです。
どういうことか、以下の枠内で説明します。
は成り立ちます。
一方で、これらを足し合わせた を考えたときに
は、一般には成り立たないわけですね。( であれば成立します。)
では、重ね合わせの原理はどのように考えたら良いのか。式 ではなく「時間に依存するシュレーディンガー方程式」を考えるべきだったのです。
式 のシュレーディンガー方程式は、正確に言えば 時間に依存しないシュレーディンガー方程式となります。
一方で次の式 は時間に依存するシュレーディンガー方程式です。
波動関数 としては、前回は座標
に対する関数として考えましたが、こちらは時刻
も含めた
の関数として
を考えることにするのです。だから「時間に依存する」というわけです。
実は、本来のシュレーディンガー方程式は式 の方なんですね。
では式 の方は何だったかというと、これは位置
と時刻
で変数分離して得られる方程式だったのです。
とおいて式 に代入すると
となりますが、これを で割ると
となり、左辺は位置 だけの関数、右辺は時刻
だけの関数となりますね。よって、定数関数です。
この定数を とおくと、これは物理的にはエネルギーという意味を持ちますが、
となります。式 が時間に依存しないシュレーディンガー方程式というわけですね。
式 は簡単に解けて
となります。
結局、係数を の方に押し付けると
は、時間に依存するシュレーディンガー方程式 の解となります。
時間に依存する因子は、絶対値をとると になるので確率分布には影響しません。だから、前回までは特に問題にならなかったわけですね。
時間に依存するシュレーディンガー方程式 の解
および
が得られたとすると、当然
が成立します。
ここで、両者の重ね合わせ を考えると、微分演算子やハミルトニアンの線形性より
が成立するわけですね。すなわち、 も時間に依存するシュレーディンガー方程式の解になるわけです。
これこそが 重ね合わせの原理 です。
さて、エネルギー を持つ2つの波動関数
の重ね合わせとして
を考えたときに、 のエネルギーはいったいどのように表せるのでしょうか。
のエネルギーは
で、
のエネルギーは
であり、
と
のどちらが観測されるかどうかは確率的に決まります。したがって、エネルギーの期待値を考えれば良いでしょう。
ここで、 のエネルギーについて考えると、
は
に対する固有関数なので
が成り立っています。これに左から の複素共役
を掛けて空間全体で積分すると
となりますが、右辺は を外に出すことができて
となります。よって
となりエネルギーが求まるわけですね。
これのアナロジーで、 と
の重ね合わせである
においても、次の式
によって、エネルギーの期待値
が求まると考えましょう。
実際、 を相異なるエネルギー(固有値)
に対応する波動関数だとしましょう。ここで、ハミルトニアン
はエルミート演算子と呼ばれるものになっており、この性質により相異なる固有値に対応する固有ベクトルは直交します。すなわち
ということです。
この事実と、波動関数 の規格化条件
を使って をより具体的に計算することができます。以下はなかなかすごい計算ですが、丁寧に1行1行読んでいけば理解できるかと思います:
得られた式を観察しましょう。
係数 の部分は重ね合わせの係数の絶対値の二乗をとって、その比率を考えたものとなっています。これは、
が観測される確率だと解釈できますね。同様に、
も
が観測される確率だと解釈できます。
すると、 はまさにエネルギーの期待値だと思うことができますね!
これにて準備が整いました。
3. 分子軌道法の計算
それでは、分子軌道法の具体的な計算を実行したいと思います。
ここから計算したいのは、水素分子のように原子核が2つある分子における、電子1つの波動関数です。

ハミルトニアン
を考えます。これはポテンシャルとして、各原子核から電子へのクーロン力と、原子核同士のクーロン力をそれぞれ考えたものとなっています。このハミルトニアンを使って、シュレーディンガー方程式
を考えるわけですね。
これは簡単に解けないので、知っている状況に帰着しようということになります。
もし仮に原子核2がなかったとすると、電子には原子核1の寄与しかありませんので、水素原子のシュレーディンガー方程式を解くことができます。
原子核 に対する水素原子の軌道に対応する波動関数を
としましょう。水素原子のときにやったように、軌道は複数取りうるわけなので、どれか1つを選びます。
(あとで、具体的な軌道について議論することになります。)
また同様に原子核2についてのシュレーディンガー方程式の解をやはり とおくことにしましょう。
ここで、原子核の距離が十分大きいとすると、つまり が十分大きいと考えると
は分子におけるシュレーディンガー方程式を近似的に満たすと考えられます。
を小さくしていくと、相互の原子核の影響を受けることになり、解の様子は
から離れていきます。
分子軌道法では、分子のシュレーディンガー方程式の真の解 は、
と
の重ね合わせによって近似できると考えます。つまり、線形結合
を考えます。これが の近似になるような
の組を探せばよい、というのがアイデアです!
前節で一生懸命説明したように、 波動関数の重ね合わせ についてのエネルギーの期待値は
で表せるのでした。これは についての 2変数関数
となっています。
変分原理によれば、分子の取りうる真の軌道のエネルギー は、必ず
を満たすはずなので、 の極小値を決定すればそれが真のエネルギーの近似値と思えるという寸法です!
さぁ、面白くなってきました!!
具体的な計算を実行するために、エネルギーの式 に
を代入して計算しましょう。
分母と分子に積分がたくさん出てきているので、それぞれ次のように置きましょう。
(
は規格化されている)
(
は規格化されている)
これらの積分は名前がついていまして、何度も出てくるので説明しておきましょう。
:クーロン積分
:規格化条件により、積分値は
となる
★ のとき:
:共鳴積分
:重なり積分
これらを使うとエネルギーの期待値は
と表すことができます。
さらに、以下の枠内の理屈により や
という性質もあるので、もう少し簡潔に
とできます。
の性質を持ちます。 も
実数なので、結果的に
であることが帰結されます。また
も同様です。
さて、これで波動関数 に対応するエネルギー(の期待値)を求めることができました。これは
の関数だと思うことができます。
変数 に対する
の最小化問題 を解いたときに、得られる解
に対応する波動関数が、分子の真の軌道の近似になっているというわけですね。
こういう方法のことを 変分法 というそうですが、要するに最小化問題だと思って差し支えないと思います。
最小化問題を解くための簡便な方法は、偏微分することです。すなわち、エネルギーを と
でそれぞれ偏微分して
を満たすような を求めればよいのです。
では、実際に偏微分を計算したいと思いますが、少し工夫します。エネルギーの式 の分母を両辺にかけて
とします。この全体を で偏微分すると
となりますが、 の形にすると
となります。
であることは、式
の分子が
になることと同値ですから
が得られます。
同様に、 で偏微分すると
も得られます。
すなわち、式 と同値な条件として
を変数とする連立方程式
が得られるわけです。
行列で表すと
ということですね。
さて、式 が
ではない解を持つための必要十分条件は
であることです。
これは完全に線形代数の問題なので、この同値性が飲み込める方はそのまま進んでいただいて、気になる方は以下の証明を読んでください。
(証明)
を示す:
仮定より は正則だから、逆行列
が存在する。これを
に左から掛けると
となり、
なる解を持たないことが言えた。
を示す:
仮定の条件を言い換えると「」ということである。行列
を
とベクトル表記し、
とすると、仮定の条件は
ということである。これは、ベクトル が一次独立であることを意味する。
ここで、一次独立なベクトルを並べた行列 は正則であることを示す。(これが言えれば、
がしたがう。)
まず行列 に対する連立方程式
を考える。これを行基本変形によって簡約化すると
が得られる。また、一次独立性より
は単位行列より、
として解が得られる。したがって、任意の
について一意に解が定まる。
ここで、基底ベクトル (
番目が
)に対して
の解を
とおく。すると行列
が定義できる。これを に左からかけると
であり、単位行列になる。右からかけても同じく単位行列になるので、 は
の逆行列である。したがって
は正則行列であり、
が言えた。
あらためて、結論をいうと式
が なる解を持つことと、式
は同値な条件ということになります。
式 は
についての方程式となっていますが、この式を 永年方程式 というそうです。ちょっと、名前がかっこいいですね!
永年方程式は
という形の方程式です。
現在は2つの原子核について考えているので 行列が出ていますが、一般の
個の原子核の場合においては
の同じ形の行列式が現れます。
さて、永年方程式 を解くために左辺の行列式を展開すると
となります。
これは についての2次方程式になっていますので、2次方程式を解けば高々2つのエネルギー
が得られます。これらに対応する解が分子軌道というわけですね。
式 のままでは計算しづらいですが、もしも
であったと仮定しましょう。これは物理的には「原子軌道 のエネルギーがそれぞれ等しい」ということを意味します。
でしたが、これは のエネルギーを求める式
において、分母を としたものになっています。
は正規化されているので、分母は
となります。
よって、 は原子軌道
のエネルギーそのものだと思うことができますね。
も同様に原子軌道
のエネルギーだと思うことできます。
はこれらのエネルギーが等しいことを表します。
つまり、① 同じ元素による2原子核を考えていて、また、② と
として同じ原子軌道を選択する、という仮定を置いている状況では、
は自然に成立するわけですね。
このような条件では より、式
は
と簡単化されます。
これは「二乗 マイナス 二乗 = 0」の形になっていますので
ということになります。つまり
が解となります。
2つの解にそれぞれ 、
と名前をつけておきましょう。
ここで、(エネルギーが負であるから)であり、
(内積なので)であることを考慮に入れると
が成り立ちます。
つまり、取りうる分子軌道は2つあって、それぞれ と
というエネルギーを持ち、
の方がよりエネルギーが低い、ということになります。この
に対応する軌道を 結合性軌道 といい、もうひとつの
に対応する軌道を 反結合性軌道 といいます。
分子軌道のエネルギーを図に表すと次のようになります:

原子核1の原子軌道 と原子核2の原子軌道
が重なり合って、2つの分子軌道(結合性軌道と反結合性軌道)が生まれます。
結合性軌道の方は、エネルギーが元の原子軌道のものよりも低く、電子はより低いエネルギーの軌道を求めて結合性軌道に入ります。こうして安定な結合が形成されるというわけです。
たしかに、エネルギーの極小値を求めると、必然的に2つの軌道が出てきますね!
結合性軌道と反結合性軌道の各エネルギー から、実際に軌道の係数
を求めてみましょう。
永年方程式の1個前の連立方程式
に、 や
を代入します。
実際、 を代入すると、1行目の式は
であり、計算すると
が得られます。
(式 の2行目からも同じ条件が得られます。)
また、 が正規化されているためには
である必要があります。
式 に式
を代入して、
を消去すると
となり
が得られます。 より
が得られるということになります。これが結合性軌道の波動関数です。
同様に、 からは、
が得られ、反結合性軌道の波動関数
が得られます。反結合性軌道の方は、波動関数の記号にアスタリスクをつけて表すのが一般的です。
さて、結合性軌道 の方は、原子軌道の符号が一致するように重なるので、強め合うように結合が形勢されるというイメージです。一方で、反結合性軌道
の方は、原子軌道の符号がちょうど反転していますので、逆に打ち消しあうようになるわけですね。
この辺のイメージは、実際の分子を想定した計算を実行することで確認してみましょう。
4. 水素分子のσ結合
より具体的な軌道を想定して分子軌道を計算し、実際に可視化を行うところまでやってみましょう。まず、最初に考えるのは 水素分子 です。
水素原子 は、1s軌道に1つの電子が入っている非常にシンプルな構造をしています。水素分子
は、各原子から
つずつ電子が供給されて、2つの電子による共有結合が生じています。

結合の方向が結合軸(原子核同士を結んだ直線方向)に沿った結合になっており、このような結合のことを σ結合 といいます。
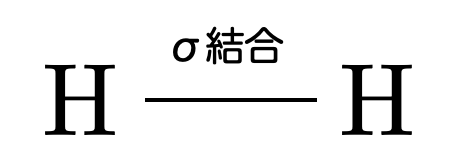
このときの分子軌道を記述するためには、2つの水素原子の1s軌道に対応する波動関数 と
を考えて、この線形結合
を考えれば良いでしょう。
今、2原子間の結合を考えており、それぞれ同じ軌道(1s軌道)同士を考えています。したがって、対称性から と仮定してよいことになります。
このとき、取りうるエネルギーは
であり、 の関係にあります。
に対応する分子軌道は2つあり、それぞれ結合性軌道と反結合性軌道というのでした。今回は、σ結合を考えているので、結合性軌道を
、反結合性軌道を
と表すことにします。
具体的には、この軌道は式 により次のように表されるのでした:
あと必要な情報としては と
です。
はクーロン積分、
は共鳴積分という名前がついているのでした。これらはエネルギーを計算するのに使う量なので、分子軌道の波動関数を計算するのには取り急ぎ必要ありません。
は重なり積分というのでした。これは、おおよそ「波動関数の重なり度合い」を表す量で、2つの原子軌道の波動関数がどれぐらい重なっているかを表します。(あまり重なっていなければ値は小さく、重なっていれば値は大きいということですね。)
各分子軌道の波動関数を計算するには が必要ですが、これには積分
を計算すれば良いことになります。
ただ、この計算は面倒なので、ここでは教科書から数値をお借りします。参考文献の教科書によると、水素原子の1s軌道同士の重なり積分の値は 程度になるそうです。これはかなり大きな値だそうで、第2周期以上の元素においては1s軌道の重なりは0.2〜0.3程度になるそうです。水素原子はだいぶ例外的なのですね。
(たしかに、 なので半径は大きいため、重なりは大きくなりそうですね。)
そこで、 としましょう。すると
となります。
実際、上記の結合性軌道と反結合性軌道の波動関数について、前回やったように「確率が90%になる領域」について可視化すると次のようになります。(プログラムはあとで紹介します。)
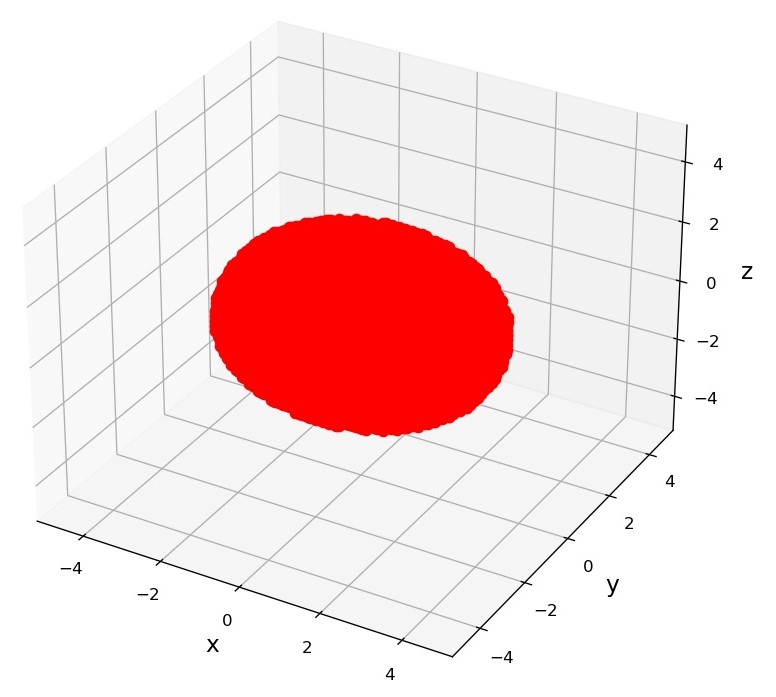
図:水素分子(1s軌道)の結合性軌道

図:水素分子(1s軌道)の反結合性軌道
前回までの記事同様、赤色は波動関数が正の部分、青色が負の部分をそれぞれ表しています。
図から、結合性軌道の方は、2つの1s軌道がくっついて結合を形成しているように見えます。一方、反結合性軌道の方は、位相が逆になっていることにより打ち消され、原子核と原子核の間の部分の確率密度が小さくなっているように見えます。
実際、反結合性軌道を 軸方向から見ると、こうなっています。
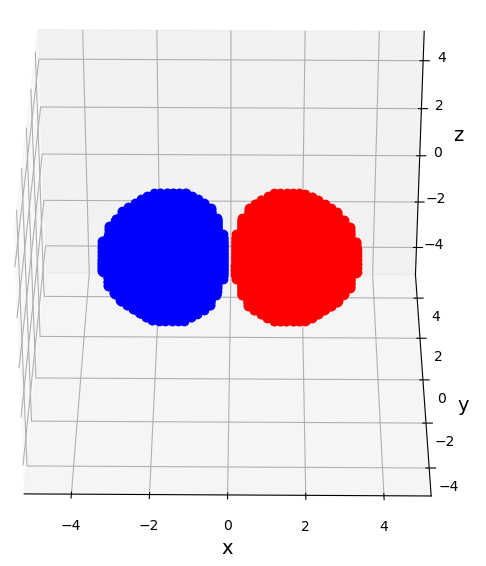
水素原子の1s軌道が近づいていくと、その重なりにより2つの安定な分子軌道が生じます。電子は各軌道にやはり2つずつ入ることができ、水素分子の場合は2つの電子が、より安定な結合性軌道に入ることになります。

結合性軌道では分子間の結合を形成します。何かの拍子に電子が不安定な反結合性軌道に入ると、上記のように電子の分布は結合部で打ち消しあい、結果的に結合が切れることになります。
なお、上記の可視化においては、2つの水素原子の位置を と
においた想定で計算しています。(つまり、原始間距離はボーア半径の2倍。)
このときの原始軌道 を計算するには、水素原子が原点に置かれているときの1s軌道の波動関数は量子数
の波動関数なので
として
のように計算すればよいですね。
5. エチレン分子のπ結合
前節はσ結合の例を紹介しました。今度は π結合 について考えたいと思います。π結合とは、σ結合と異なり、結合方向と直角の方向を向いた原子軌道同士の結合のことです。
具体的には、エチレン分子 について考えてみましょう。
炭素原子には全部で6つの電子があり、内訳はK殻(1s軌道)に2個、L殻(2s軌道と2p軌道)に4個となっています。つまり、価電子(最外殻電子)は4つです。
エチレンの炭素同士は、炭素原子核1からは価電子のうち2個、もう一方の炭素原子核2からも価電子のうち2個、それぞれ2個ずつの電子を供給しあって結合しています。このような結合を二重結合というのでした。
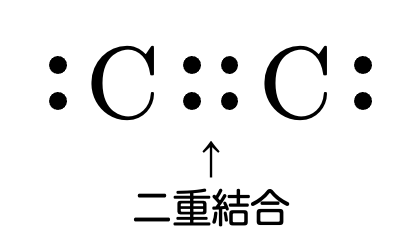
この二重結合の内訳ですが、1本目が原子核の結合方向を向いた原子同士による結合(つまりσ結合)と、結合方向と垂直な方向を向いた原子軌道による結合(つまりπ結合)となっています。

π結合のイメージ
ここではこのπ結合にフォーカスしましょう。p軌道の方向を 軸とすると、π結合を構成する原子軌道は原子核1の
軌道と、原子核2の
軌道ということになります。
として、水素分子のときと同様に計算を行うと、結合性軌道
・反結合性軌道
の波動関数はそれぞれ
となります。π結合なので、波動関数の記号は の記号を用います。
対応するエネルギー は
となるのでした。
ここでやはり、 の値が必要になります。
は計算するか、実験的に調べるしかありません。ひとまず定数として
と置いておきましょう。( となります。)
π結合における重なり積分は、あとで述べるヒュッケル法という考え方によって としてよいことが分かります。
したがって、結合性軌道 と反結合性軌道
は
となり、対応するエネルギーは
と簡単に求められます。
それでは、これらの分子軌道の様子を可視化してみましょう。
原子核の距離は、エチレンの炭素間の結合距離は 133.9 pm だそうなので、距離が ボーア半径になるように炭素原子核を配置します。
すなわち
ということです。
また、炭素電子の2p軌道なので、有効核電荷は
となります。
# 記事の一番最後に完全版のプログラムを掲載します。 # エチレン分子のπ_2p軌道 def ethylene_molecule(x, y, z, id): Z = 6 # 炭素原子を想定しているので Z = 6 Z_eff = Z - (0.35*3 + 0.85*2) # 有効核電荷(スレータ―則により計算) n = 2 l = 1 m = 0 distance = 133.9/52.9 # 水素原子のボーア半径 52.9 pm, エチレン分子の原子間距離 133.9 pm if id == 0: # π_2p軌道(結合性軌道) return (f(x-distance/2, y, z, n, l, m, Z_eff)/np.sqrt(2.0)) + (f(x+distance/2, y, z, n, l, m, Z_eff)/np.sqrt(2.0)) else: # π_2p*軌道(反結合性軌道) return (f(x-distance/2, y, z, n, l, m, Z_eff)/np.sqrt(2.0)) - (f(x+distance/2, y, z, n, l, m, Z_eff)/np.sqrt(2.0))
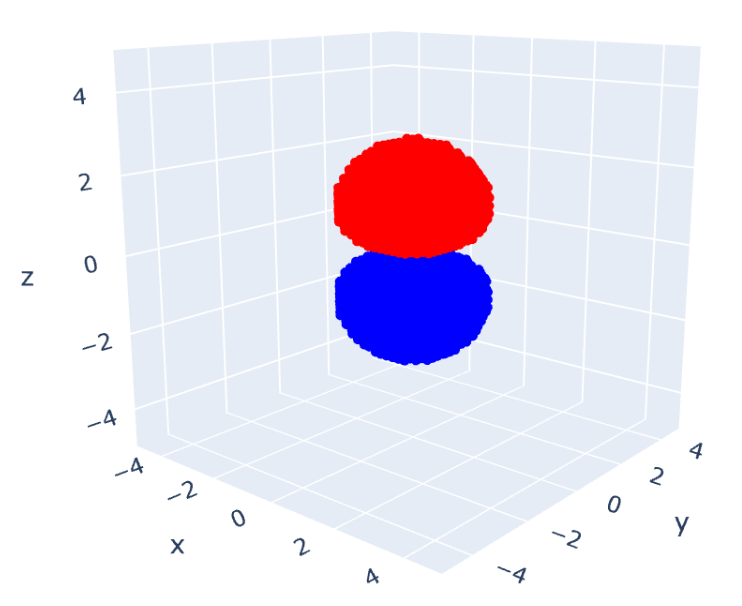
先ほどと同様のプログラム(最後にまとめて紹介します)で可視化したものが次の図になります。
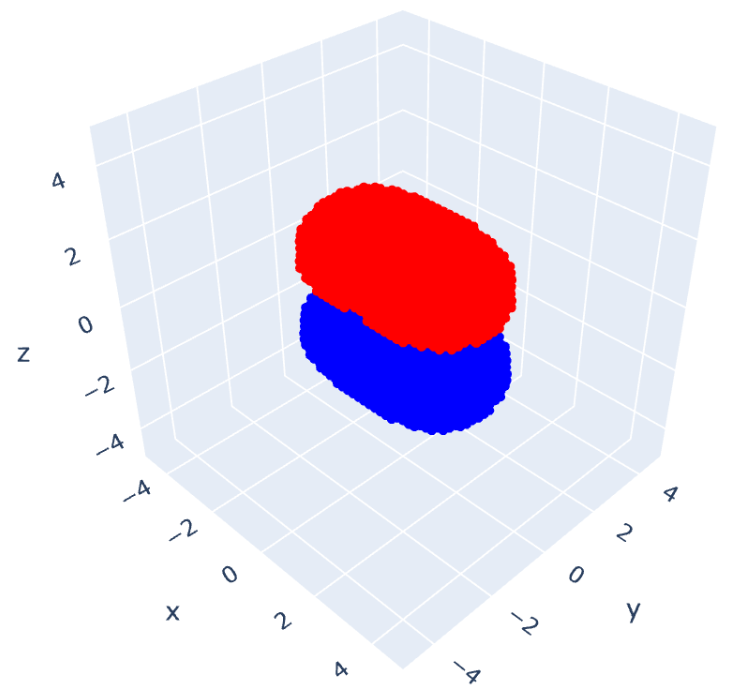
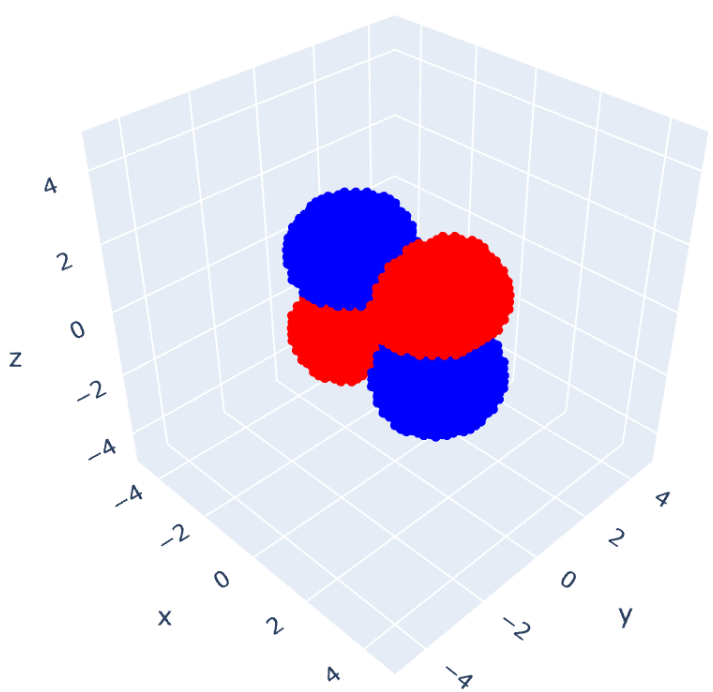
左側が結合性軌道 で、右側が反結合性軌道
です。(波動関数が正の部分を赤色、負の部分を青色で表示しています。)
結合性軌道の方は、位相が揃っているので、分子に対してz軸方向上側と下側にそれぞれ電子雲ができていて、結合を形成しているように見えますね。
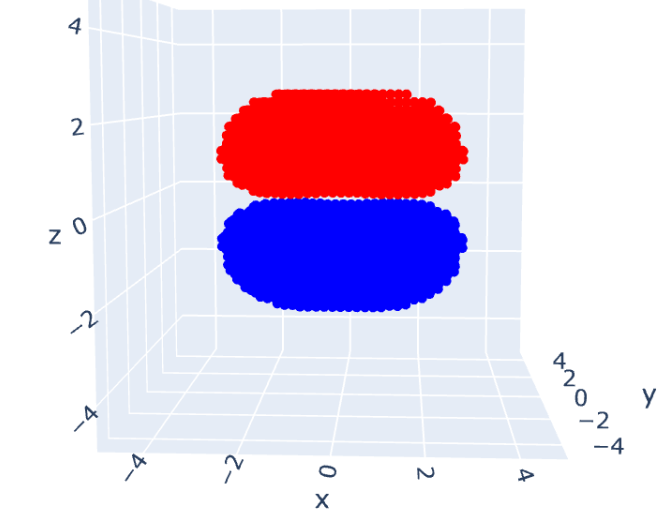
一方、反結合性軌道の方は、位相が反転している関係で分子間には「ちょうど電子が存在しない部分」ができているように見えます。
エネルギーについて見てみると、以下のようになります。

水素分子のときと同じように、原子軌道( 軌道)のエネルギーに対して、上下に2つの軌道が生まれます。エネルギーの低い方が結合性軌道で、高い方が反結合性軌道です。
また、 と近似したことによって、エネルギーが
と対称的になったことが重要なポイントです。(
を中心に、
だけ上下しています。)
エチレンの場合は、炭素原子の 軌道電子が各1つずつ分子軌道に入るわけですが、2個なのでどちらも結合性軌道に入ります。どちらも結合性軌道に入るということで、安定した結合が形成されるようです。

電子2つはどちらも結合性軌道
6. ヒュッケル法とブタジエンのπ電子共役系
前節では分子として2炭素原子核によって構成されたものを考えてきましたが、ここからは原子核の数を増やしてみたいと思います。
例としてブタジエン を考えたいと思うのですが、炭素だけに着目すると構造式は次のようになります。

他にも、二重結合の位置が異なる1-2ブタジエンという構造異性体がありますが、今回は扱いません。
4つの炭素原子を左から1,2,3,4と名前をつけることにします。
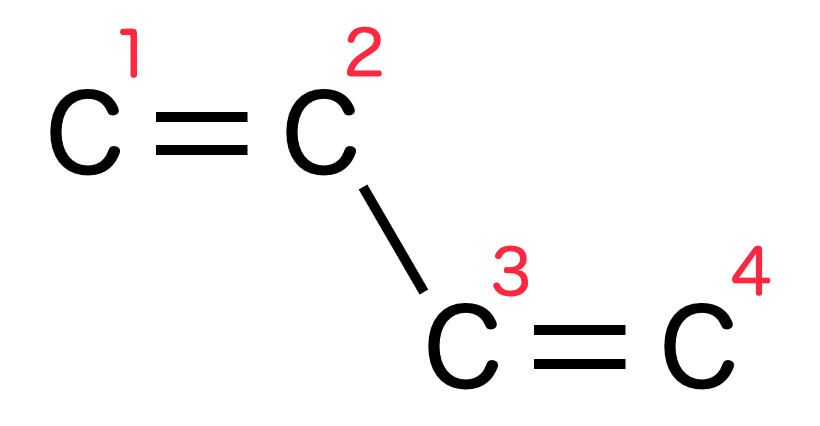
二重結合が1-2間, 3-4間にありますが、π結合の電子は必ずしも1-2間, 3-4間にのみあるわけではありません。実際は、1,2,3,4の炭素全体にまたがって存在しているのです。こういう状況を 非局在化 といいます。
(ブタジエンのように)二重結合・単結合が交互に並んだ結合において、π電子が非局在化しているような系を一般に π電子共役系 といいます。

ブタジエンにおいては、分子を構成する4つの炭素原子にはそれぞれ 軌道
があります。π電子が非局在化している分子軌道に対しては、これらの重ね合わせ(つまり線形結合)
を考えることになるわけです。
あとは、この軌道に対するエネルギーの期待値
を計算し、この極値を求めるとそれが分子軌道になるわけですね。
実際
なる解を求めようとすると、 変数の連立方程式が得られます。
この連立方程式が なる解を持つことと同値な条件として、
という形の条件が得られます。具体的には
となりますが、これを永年方程式というわけですね。 は定数なので、これは
についての4次方程式となります。
実際に、解くにあたっては、 をそれぞれ計算するわけですが、ちゃんと積分計算していくのはなかなか大変です。手計算では無理そうです。
そこで思い切った近似が必要になります。ここで使えるのが ヒュッケル法 です。
まず、ヒュッケル法はブタジエンのような π電子共役系 で適用できる近似手法です。このような状況で、次のような近似を行います:
重なり積分 の方はわかりやすいですね。
は
の全空間での確率なので規格化条件より
であり、
の場合は
と近似するというわけです。(波動関数同士の「重なり」がほとんどないと解釈できそうです。)
一方の は少し難しいルールですね。
の方は、原子核はすべて対等であるということで、定数としているわけです。(
はクーロン積分というのでした。)
の場合は、原子核
と
の間にσ結合があるかないかで値が決まります。今考えているのは、π電子なわけですが、σ結合があるということはその原子核間で結合があるということですね。その場合は
(定数)となります。そうでない場合は、要するに直接つながっていない原子核同士ということなので、その場合は
とするわけです。(
の
を共鳴積分というのでした。)
たとえば、ブタジエンの場合は の間にはσ結合があるので
です。一方、
や
の間にはσ結合はないので、
というわけです。
さて、ヒュッケル法を用いて永年方程式 を計算すると、次のようになります:
ずいぶんと簡単な、そして対称的な形の行列式になりましたね。
ある1列をある定数 について
倍した行列の行列式は、元の行列式の
倍になります。これを使って、上記の行列の各列をすべて
倍すると
となり、 とおくと
となります。
あとは式 の行列式を計算すれば良いですね! まさに線形代数の世界です!
- 対角成分が
の間にσ結合があれば
、そうでなければ
というルールによって生成されます。そのため、機械的に導くことができます。
行列式 ですが、手計算はそれなりに大変です。
まず、 の行列式をそのまま計算するのは大変なので、第1列を使って余因子展開します。
これが に一致するので
であり、よって
の4つが解となります。
だったことを思い出すと
であり、よって
となります。
つまり、分子軌道のエネルギーとしては
の4つが取り得て、 を考慮に入れると
となることがわかります。
つまり、エチレンの場合は結合性軌道と反結合性軌道の2つがあったわけですが、ブタジエンにおいては4つの分子軌道に分かれるというわけですね!
これらの4つに対応する軌道は、連立方程式
に対して に対応する
を代入して計算できます。
加えて の規格化の条件
を適用すると、 に対応する
がそれぞれの
で求まります。
計算は飛ばしますが、対応する分子軌道の波動関数は
となります。
ようやく分子軌道が計算できたので、この波動関数をプログラムで表現し可視化してみましょう。
ブタジエンの座標を図のようにおきます。
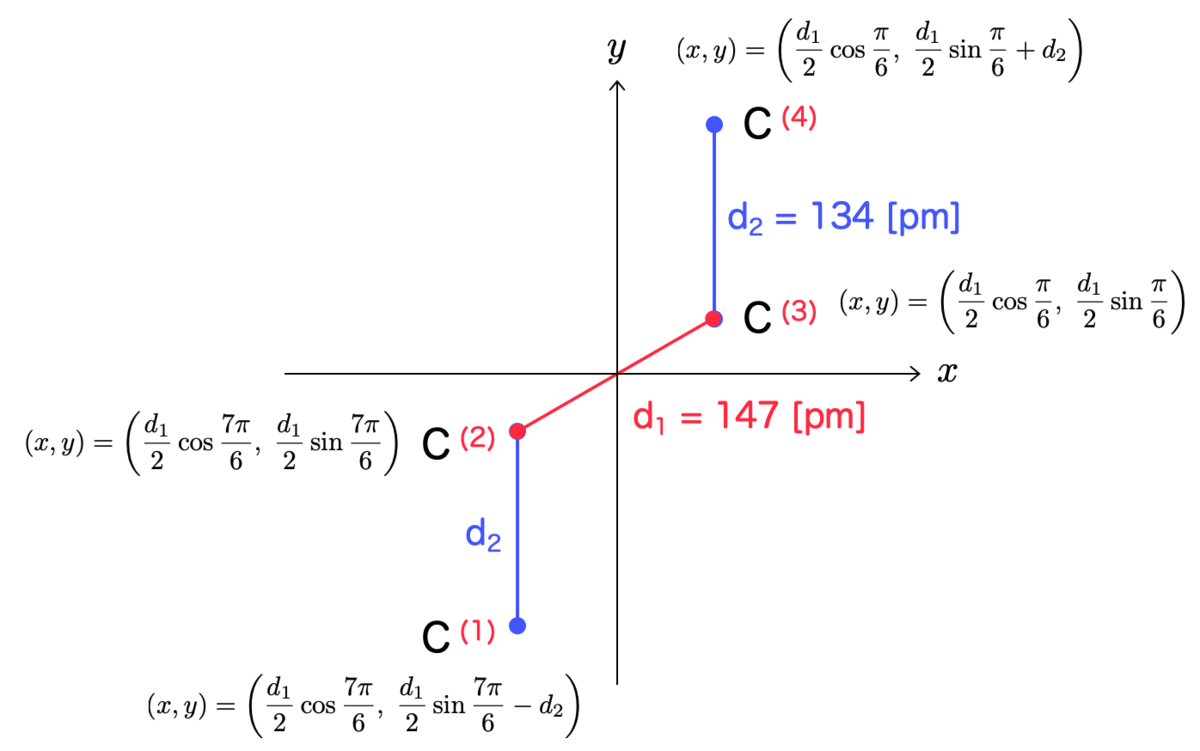
これを踏まえて、ブタジエンの波動関数を計算する関数を以下のように定義します:
# 記事の一番最後に完全版のプログラムを掲載します。 # ブタジエンのπ電子共役系 # http://www.nishino-labo.jp/pdf/enshu01_03_2012.pdf (原子間距離の参考) def butadiene_molecule(x, y, z, id): Z = 6 # 炭素原子を想定しているので Z = 6 Z_eff = Z - (0.35*3 + 0.85*2) # 有効核電荷(スレータ―則により計算) n = 2 l = 1 m = 0 distance_1 = 147.0/52.9 # 水素原子のボーア半径 52.9 pm, C2-C3の原子間距離 147.0 pm distance_2 = 134.0/52.9 # 水素原子のボーア半径 52.9 pm, C1-C2, C3-C4の原子間距離 134.0 pm # 各炭素原子の中心座標 center = [ [0.5 * distance_1 * np.cos(7.0*np.pi/6.0), 0.5 * distance_1 * np.sin(7.0*np.pi/6.0) - distance_2], [0.5 * distance_1 * np.cos(7.0*np.pi/6.0), 0.5 * distance_1 * np.sin(7.0*np.pi/6.0)], [0.5 * distance_1 * np.cos(np.pi/6.0), 0.5 * distance_1 * np.sin(np.pi/6.0)], [0.5 * distance_1 * np.cos(np.pi/6.0), 0.5 * distance_1 * np.sin(np.pi/6.0) + distance_2], ] # 係数 c = [ [0.372, 0.602, 0.602, 0.372], [0.602, 0.372, -0.372, -0.602], [0.602, -0.372, -0.372, 0.602], [-0.372, 0.602, -0.602, 0.372], ] res = 0.0 for i in range(4): x0 = x - center[i][0] y0 = y - center[i][1] res += f(x0, y0, z, n, l, m, Z_eff) * c[id][i]
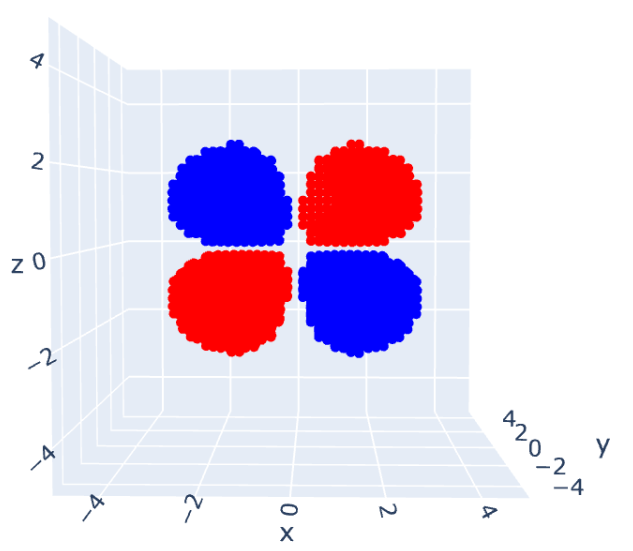
これを可視化したのが次の図になります:
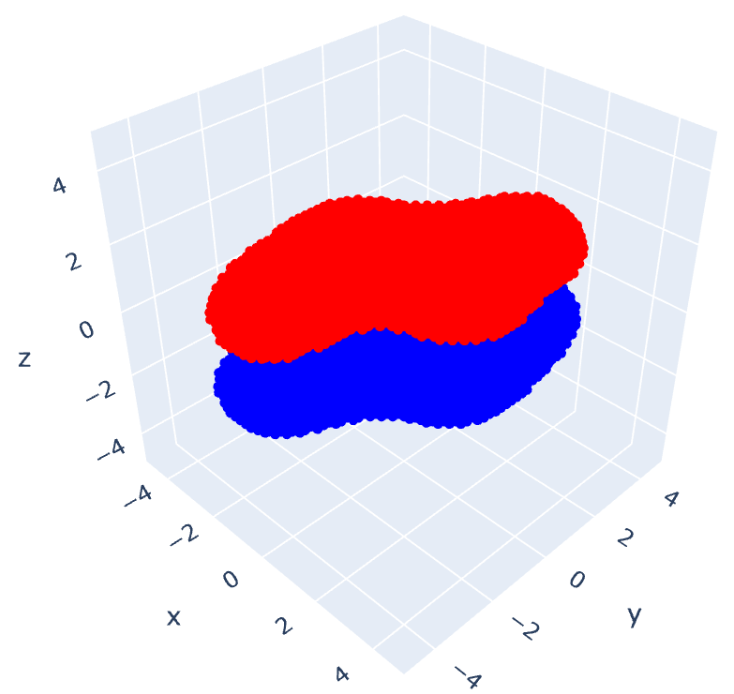
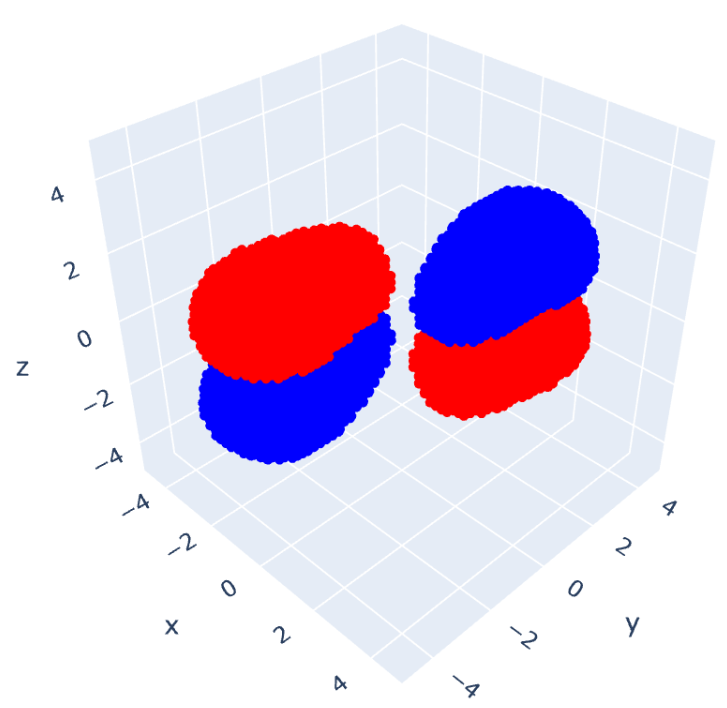

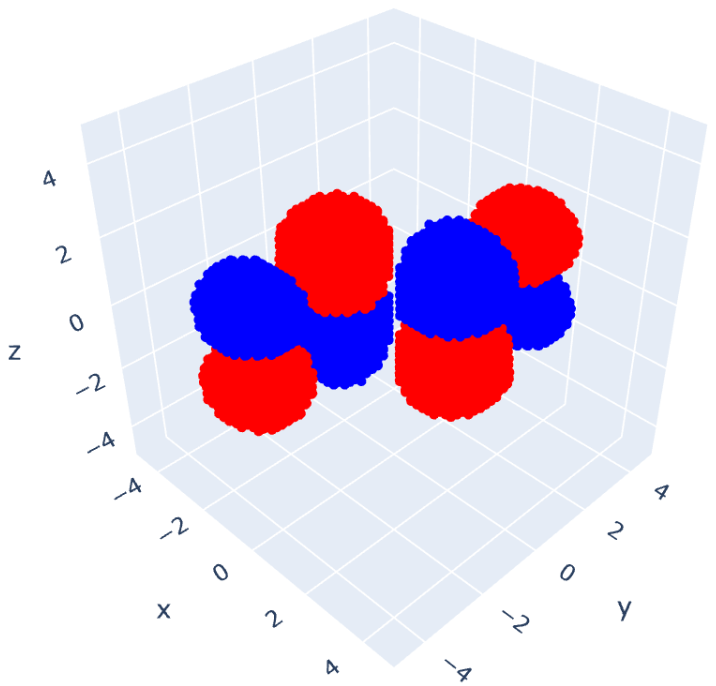
左上が 、右上が
、左下が
、右下が
です。
エネルギー図に表すと次のようになります。

さて、ここでπ電子の行き先について考えましょう。
ブタジエンの各炭素原子の 軌道から全部で4つの電子が生じますが、これらがエネルギーが低い軌道から各2つずつ入っていきます。したがって、
(エネルギーは
)に2つの電子が入り、
(エネルギーは
)に2つの電子が入ります。

したがって、電子は最大で のところまでしか入らないというわけですね。
には空の軌道ということになります。
ここで一つ重要な用語を紹介したいのですが、電子によって占有されている最もエネルギーが高い軌道のことを HOMO(Highest Occupied Molecular Orbital) といい、電子が空であるような最もエネルギーが低い軌道のことを LUMO(Lowest Unoccupied Molecular Orbital) といいます。
この用語を使うと、ブタジエンのπ電子共役系においては、HOMOが であり、LUMOは
ということになります。
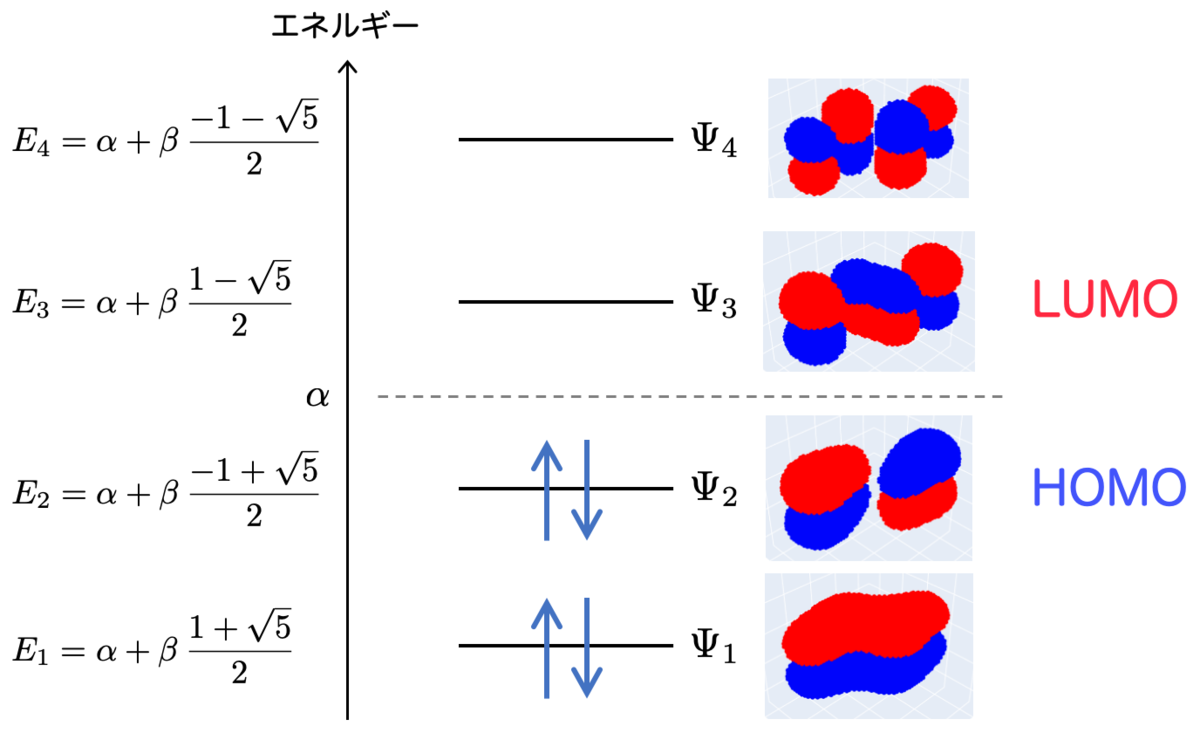
HOMO-LUMOを考えるモチベーションとしては、HOMOの電子の反応しやすさが挙げられます。
HOMO-LUMOを起点として、種々の化学反応を説明する フロンティア軌道理論 というものがあるそうです。今回は触れることはできませんが、とにかくそういう考え方があるのですね。
光の吸収 という観点でもHOMO-LUMOを考えるのは重要です。
日曜化学(1)の記事では、こんなことを書いていました。水素原子に振動数 の光が入ってきたとき、電子がより高いエネルギーの軌道(励起状態)に遷移することがあります。遷移する条件はエネルギー差が
にちょうど一致することです。これは分子軌道でも同じことです。
すなわち、ちょうどエネルギー差が に一致する光が入射すると、HOMOの電子が光を吸収してLUMOに励起するというわけです。

エチレン(二重結合1つ)とブタジエン(二重結合2つ)を考えましたが、同じ要領で二重結合/単結合のセットを増やしていくと、分子軌道の数が と増えていきます。
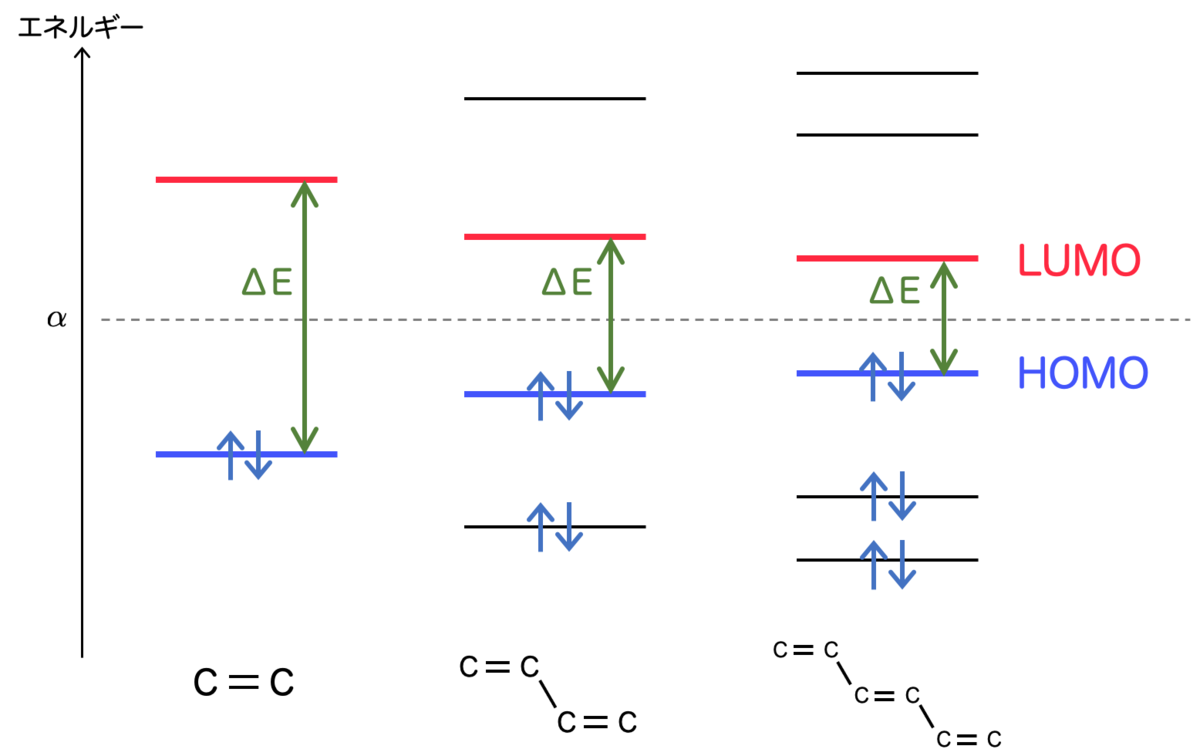
図の右に行けば行くほど、HOMOとLOMOの間のエネルギー差はどんどん小さくなっていきます。よりエネルギーの小さい(つまり、長い波長)の光を吸収するようになるということに他なりません。
こんな風に、分子軌道のエネルギーというのは、吸収する光の波長と大変関係が深い ということですね。吸収する光の波長が可視光であれば、物質の色にも影響を与えることになります。
たとえば、β-カロテン という物質を考えましょう。ニンジンの中に入っている橙色の色素成分です。これはβ-カロテンの分子が補色である青色の光を吸収するからなのですが、この青色を吸収する仕組みが分子軌道からわかるのです。
β-カロテンの分子は、以下のような構造をしています:
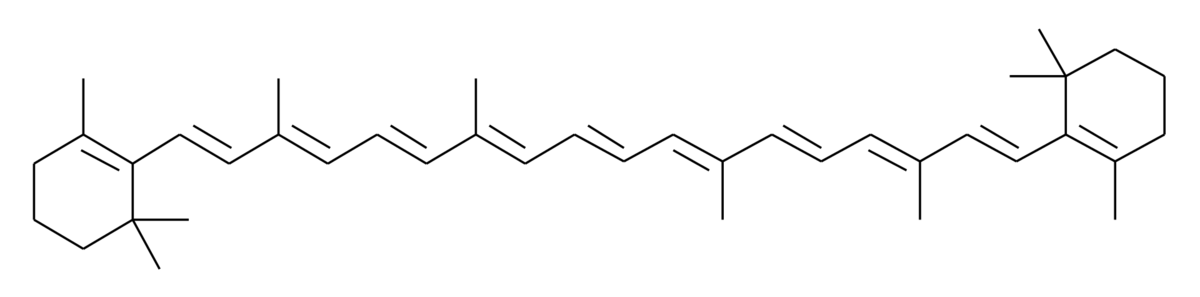
二重結合が全部で11個 あります。ブタジエンの議論の延長で、炭素22個によるπ電子共有系を考えると、HOMO/LUMOのエネルギー
であることが計算できます。したがって、エネルギー差は
となります。これはエチレンのHOMO-LUMO間のエネルギー差の 以下です。より低い振動数の(つまり長波長の)光を吸収できるようになるというわけですね。これによって可視光の波長を吸収することができるようになるわけです。
こんな風に分子軌道法によって、我々が見ているものの「色」を分子軌道から説明できる可能性があるのです。これは面白くてたまらないですね!
次回(最終回)の記事では、これまでの量子化学の理論を踏まえて、「とある身近な色」の仕組みについて考えていきたいと思います。
7. ベンゼンのπ共有系
最後の例として ベンゼン を扱いたいと思います。
ベンゼン は二重結合と単結合が交互に並んで、円環状の構造を持つ分子です。

ベンゼン分子も二重結合を含むので、π電子が関係します。
二重結合と単結合が交互になっているからといって、π電子が各二重結合に局在化しているわけではありません。ブタジエンで考えたように、π電子が分子全体に広がって分布するようになります。こういう系をπ電子共役系というのでした。
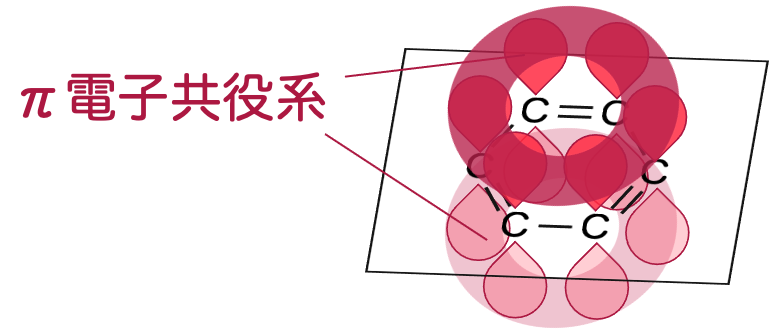
ベンゼン分子のπ電子共役系の分子軌道を計算してみましょう。図の上にある炭素原子を として、そこから時計回りに
という名前をつけましょう。

対応する 軌道の原子軌道を
として、その重ね合わせとして波動関数
を考えます。対応するエネルギー(の期待値)は計算できて6変数 の関数になるわけですが、この極値を求めると分子軌道が得られるというわけですね。
ここまで丁寧に計算してきましたので、今回は途中の議論を省略して考えたいと思います。
まず、ヒュッケル法を用いて永年方程式を計算すると、次のようになります。
ベンゼンは環構造になっているので、 番の炭素と
番の炭素がつながっていることに注意しましょう。(行列の1-6成分と6-1成分に
があることに注意。)
すべての列を で割って
とおくと
となります。あとはこれを解けば分子軌道のエネルギーが得られます。
この計算は大変そうだなと思っていたら、木村巌先生( @iwaokimura )からSagemathを使えば計算できると教えていただいたので、これを使っていきます。
を固有値だと思うと、上の行列式は固有多項式(characteristic polynomial)だと思うことができます。これを使って、Sagemathで上記の行列から
を引いた行列
について、固有多項式を計算します。
A = Matrix(QQ, [[0, 1, 0, 0, 0, 1], [1, 0, 1, 0, 0, 0], [0, 1, 0, 1, 0, 0], [0, 0, 1, 0, 1, 0], [0, 0, 0, 1, 0, 1], [1, 0, 0, 0, 1, 0]]); A p = B.characteristic_polynomial(); p factor(p)
実行すると、次が得られます。
[0 1 0 0 0 1] [1 0 1 0 0 0] [0 1 0 1 0 0] [0 0 1 0 1 0] [0 0 0 1 0 1] [1 0 0 0 1 0] x^6 - 6*x^4 + 9*x^2 - 4 (x - 2) * (x + 2) * (x - 1)^2 * (x + 1)^2
つまり
ということですね。あっという間に計算できてしまいました。
を思い出して、これが
なる解を求めると、次の4つが解となります。(重複度も含めると6つ。)
(重複度:2)
(重複度:2)
エネルギーの大小関係は、 を考慮して
となります。
対応する波動関数も、固有ベクトルを計算することで求めることができます。
A.eigenvectors_left()
Sagemathでこれを実行すると、こうなります(見やすいように少し整形しています):
[ (2, [(1, 1, 1, 1, 1, 1)], 1), (-2, [(1, -1, 1, -1, 1, -1)], 1), (1, [(1, 0, -1, -1, 0, 1), (0, 1, 1, 0, -1, -1)], 2), (-1, [(1, 0, -1, 1, 0, -1), (0, 1, -1, 0, 1, -1)], 2) ]
出力の形式としては、以下のようになっています:
[
(固有値1, [(固有ベクトル11, 固有ベクトル12, ..., 固有ベクトル1n), 固有値1の重複度),
(固有値2, [(固有ベクトル21, 固有ベクトル22, ..., 固有ベクトル2m), 固有値2の重複度),
...
]
固有値 (エネルギーは
)に対応する固有ベクトルは
ということになります。
正確にいうと、定数 をかけた
が、この固有値に対応する固有ベクトル全体となります。言い換えると、これがエネルギー
の波動関数全体(の空間)ということになります。これを
によって規格化すると、分子軌道
が得られます。
ここで注意したいのは、重複度が2以上のときです。重複度 の固有値に対応する固有ベクトルの次元は
次元になるということを考慮する必要があるからです。(重複度が2であれば2次元。)
たとえば、固有値 (エネルギーは
)に対応する固有ベクトルの次元は
となるわけですが、2次元なので基底が2個となります。実際
が基底となります。固有ベクトル全体の空間は
となります。
ところで、今たまたま上のような基底 をとっていますが、基底の取り方は特に決まっているわけではありません。つまり、基底を取り直しても何ら問題ないということです。
ここではひとまず
を基底として選ぶことにしましょう。(特に意味はないのですが、参考文献の教科書の波動関数に合わせるためです。)
規格化すると、対応する波動関数は
となります。
こんな要領で、各固有値に対応する6つの分子軌道が次のように得られます:
さて、これにてベンゼンのπ電子共役系の分子軌道がすべて求まりました。いよいよ分子軌道を可視化したいと思います!
まず、ベンゼンの炭素原子 の座標は
のように設定します。
これを踏まえて分子軌道の波動関数を以下のように定義します。
# 記事の一番最後に完全版のプログラムを掲載します。 # ベンゼン分子のπ電子共役系 def benzene_molecule(x, y, z, id): Z = 6 # 炭素原子を想定しているので Z = 6 Z_eff = Z - (0.35*3 + 0.85*2) # 有効核電荷(スレータ―則により計算) n = 2 l = 1 m = 0 distance = 139/52.9 # 水素原子のボーア半径 52.9 pm, ベンゼン分子の炭素間距離 139 pm # 各炭素原子の中心座標 center = [] for i in range(6): cx = distance * np.sin(2*i*np.pi/6) cy = distance * np.cos(2*i*np.pi/6) center.append([cx,cy]) # 係数 c = [ [1/np.sqrt(6), 1/np.sqrt(6), 1/np.sqrt(6), 1/np.sqrt(6), 1/np.sqrt(6), 1/np.sqrt(6)], [1/np.sqrt(3), 1/(2.0*np.sqrt(3)), -1/(2.0*np.sqrt(3)), -1/np.sqrt(3), -1/(2.0*np.sqrt(3)), 1/(2.0*np.sqrt(3))], [0.0, 1/2.0, 1/2.0, 0.0, -1/2.0, -1/2.0], [1/np.sqrt(3), -1/(2.0*np.sqrt(3)), -1/(2.0*np.sqrt(3)), 1/np.sqrt(3), -1/(2.0*np.sqrt(3)), -1/(2.0*np.sqrt(3))], [0.0, 1/2.0, -1/2.0, 0.0, 1/2.0, -1/2.0], [1/np.sqrt(6), -1/np.sqrt(6), 1/np.sqrt(6), -1/np.sqrt(6), 1/np.sqrt(6), -1/np.sqrt(6)], ] res = 0.0 for i in range(6): x0 = x - center[i][0] y0 = y - center[i][1] res += f(x0, y0, z, n, l, m, Z_eff) * c[id][i] return res
これを可視化したものが次の6つの図となります。
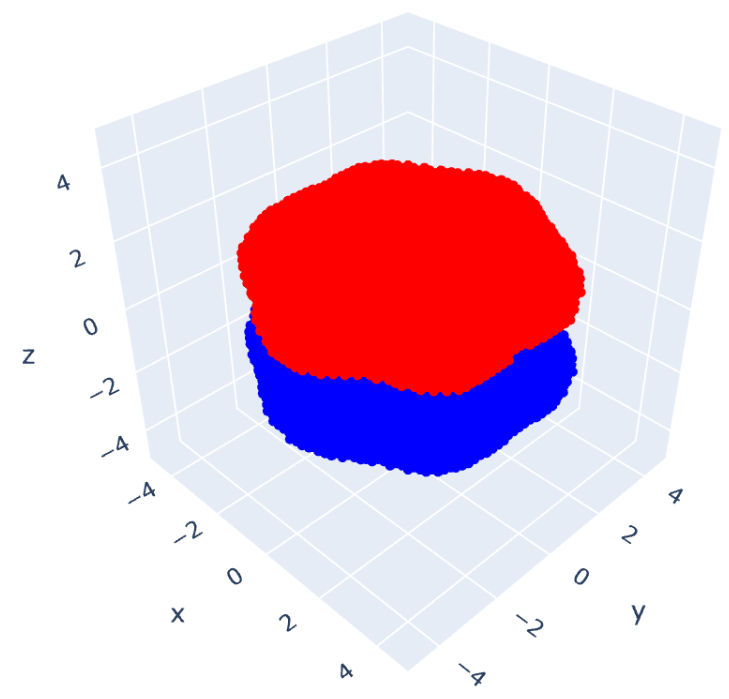
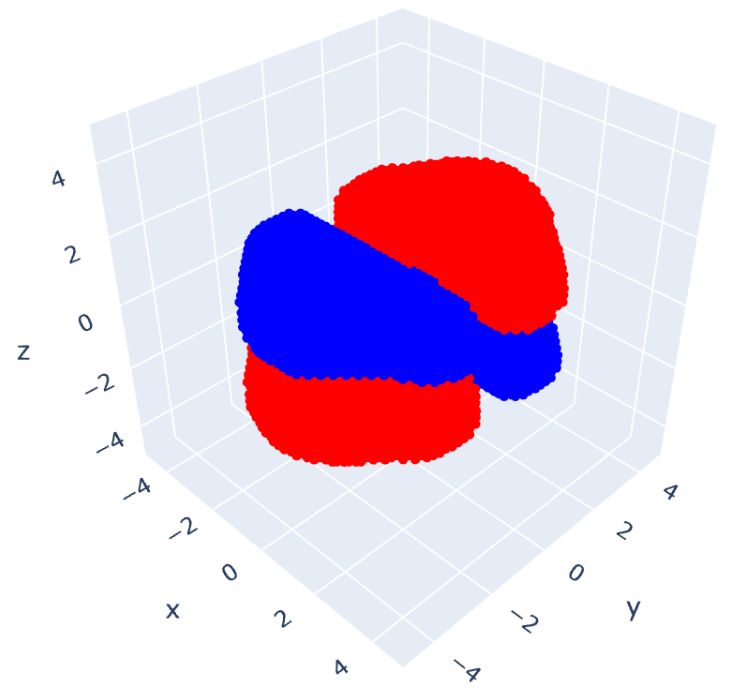
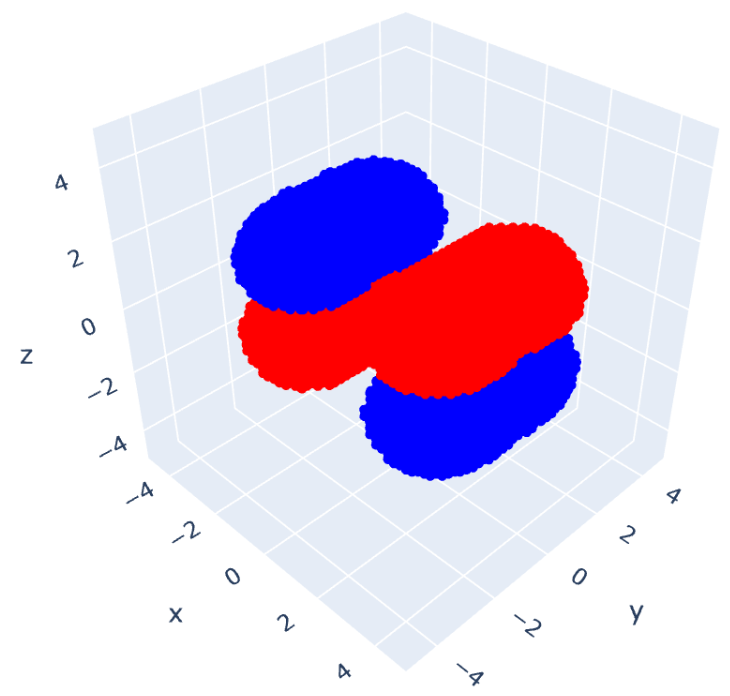
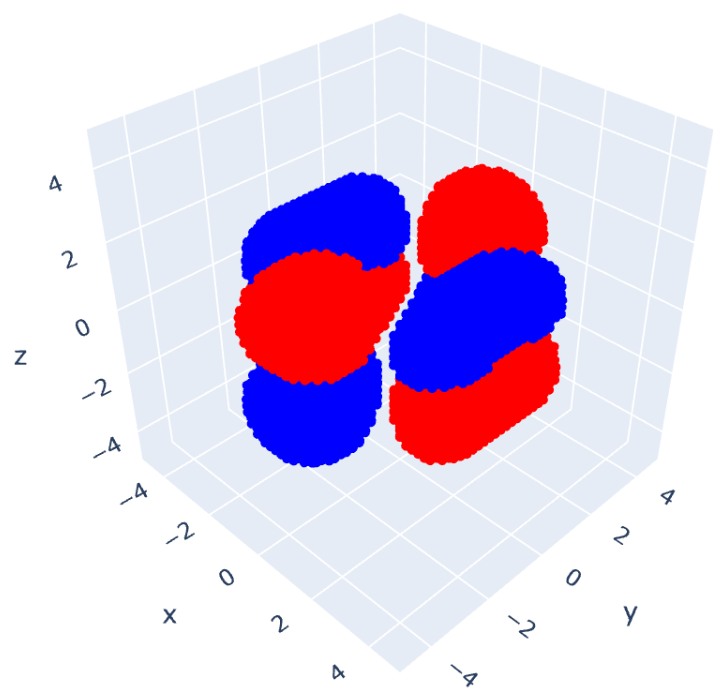
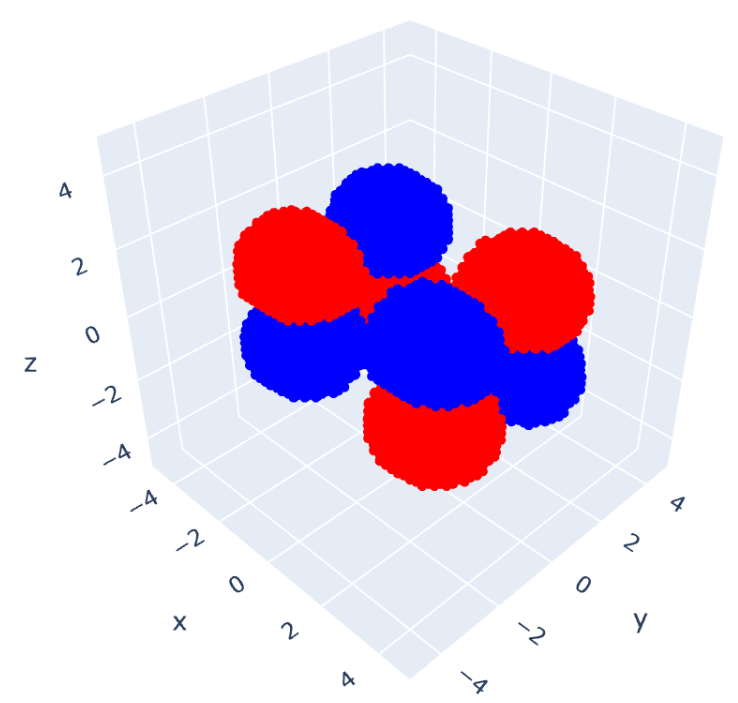
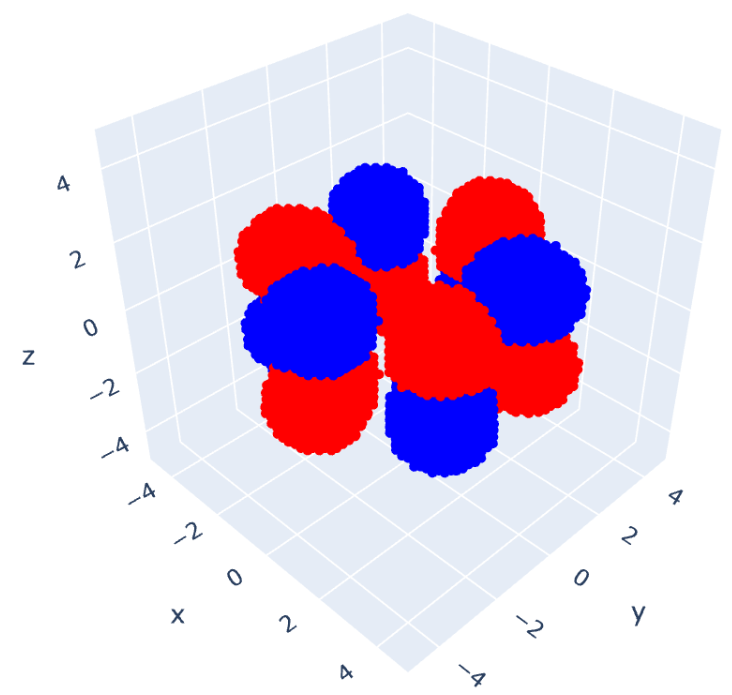
ベンゼンのエネルギー図を書くと次のようになります。
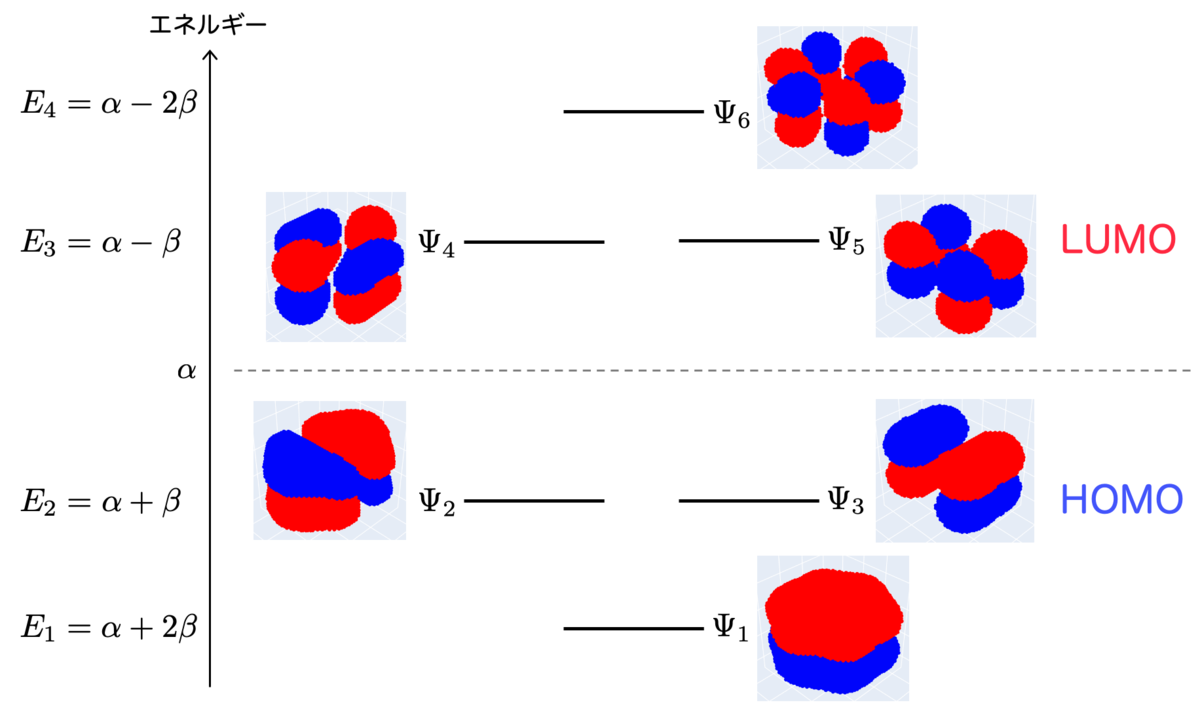
炭素原子の 軌道から計
つの電子が供給されるので、これが分子軌道にエネルギーが低い方から入っていきます。したがって、
までの軌道が充填されHOMOとなり、
がLUMOとなるわけですね。
8. 分子軌道の可視化のためのPythonプログラム
最後に、これまで可視化に使ってきたプログラムを紹介して終わりにします。
日曜化学シリーズを通して、Pythonのmatplotlibを使った可視化を行っています。したがって、以下のライブラリを事前にインストールする必要があります。
- numpy
- matplotlib
また、可視化方法としてmatplotlibではなく、Plotlyというライブラリを使ったバージョンを使いたい方は、Plotlyもインストールしておいてください。
(今回の記事の図は、すべてPlotlyを使用しています。)
可視化においては、第2回(日曜化学(2):3次元空間における電子雲の計算(Python/matplotlib))の記事内で紹介した方法3を用いています。
得られた分子軌道の波動関数 に対して、確率密度関数
の値が高い順に点を表示していき、確率が 90% になった段階でやめる、という方法を使って可視化しています。
ただし、分子軌道の計算にあたって方法3と少し変えた部分があり、その点を注意しておきます。
ヒュッケル法を適用するときに、 と近似していました。この影響で「分子軌道の確率密度関数
を全空間で積分したときの値が
に一致しない」という問題が発生します。
分子軌道 を全空間で積分すると
となります。
は本当は
ではないですが、
として、
となるように係数
を決めるのがヒュッケル法でした。ところが、こうしてしまうと
の時点で
になってしまうので、確率全体としては
の分だけずれが生じるわけですね。そのため、全空間の確率が
を下回ったり、
を超えてしまったりするわけです。
これは前回紹介した可視化方法「確率90%の領域を描画する」においてクリティカルな問題となります。全空間での確率の総和が90%を下回ってしまう場合が起きてしまうからです。(たとえば、エチレンの 軌道の絶対値の二乗を
の範囲で積分すると、
程度の積分値になります。)
この状況下でアルゴリズムをそのまま実行した結果、全領域を描画してしまうことになります。結果的に全域が真っ赤(真っ青)になってしまうのです。
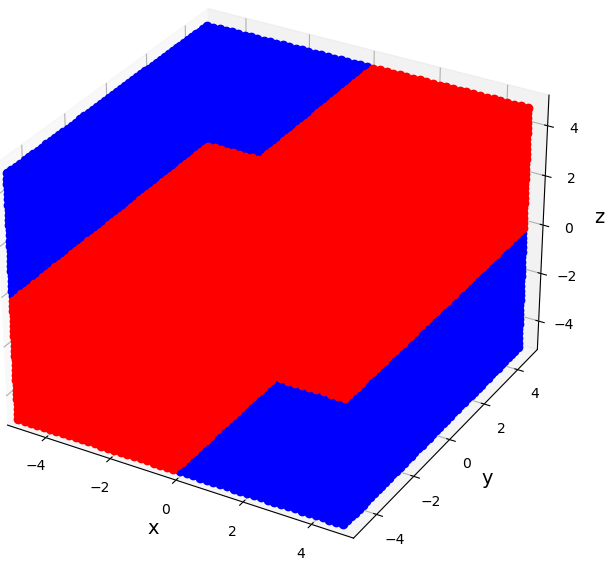
それでは困りますね。今回は、とりあえずの対策として「あらかじめ全空間の積分を計算しておき、その90%の領域を描画する」というようにプログラムを修正しました。一応、それっぽい描画にはなるので、ひとまずの解決としていますが、私の中で納得はいっていないので後々修正するかもしれません。
# 「90%サンプリング」による分子軌道の可視化 import numpy as np import matplotlib.pyplot as plt import mpl_toolkits.mplot3d.axes3d as axes3d import math # 動径波動関数(ボーア半径を a_0 = 1 に正規化) def radial_wave_function(r, n, l, Z_eff): rho = 2.0 * Z_eff * r / n if n == 1 and l == 0: return (Z_eff ** 1.5) * np.exp(-rho/2.0) * 2.0 elif n == 2 and l == 0: return (Z_eff ** 1.5) * np.exp(-rho/2.0) * (2.0 - rho) / (2.0*np.sqrt(2.0)) elif n == 2 and l == 1: return (Z_eff ** 1.5) * np.exp(-rho/2.0) * rho / (2.0*np.sqrt(6.0)) elif n == 3 and l == 0: return (Z_eff ** 1.5) * np.exp(-rho/2.0) * (6.0 - 6.0*rho + rho**2) / (9.0*np.sqrt(3.0)) elif n == 3 and l == 1: return (Z_eff ** 1.5) * np.exp(-rho/2.0) * (4.0 - rho) * rho / (9.0*np.sqrt(6.0)) elif n == 3 and l == 2: return (Z_eff ** 1.5) * np.exp(-rho/2.0) * (rho**2) / (9.0*np.sqrt(30.0)) # 球面調和関数(ただし、実関数表示したもの) def spherical_harmonics(theta, phi, l, m): if l == 0: if m == 0: # l=0, m=0 return np.sqrt(1.0/(4*np.pi)) if l == 1: if m == 0: # l=1, m=0 return np.sqrt(3.0/(4.0*np.pi)) * np.cos(theta) if m == 1: # l=1, m=+1 return np.sqrt(3.0/(4.0*np.pi)) * np.sin(theta) * np.cos(phi) if m == -1: # l=1, m=+1 return np.sqrt(3.0/(4.0*np.pi)) * np.sin(theta) * np.sin(phi) if l == 2: if m == 0: return np.sqrt(5.0/(16.0*np.pi)) * (3.0*(np.cos(theta)**2) - 1.0) if m == 1: return np.sqrt(15.0/(4.0*np.pi)) * np.cos(theta) * np.sin(theta) * np.cos(phi) if m == -1: return np.sqrt(15.0/(4.0*np.pi)) * np.cos(theta) * np.sin(theta) * np.sin(phi) if m == 2: return np.sqrt(15.0/(16.0*np.pi)) * (np.sin(theta)**2) * np.cos(2*phi) if m == -2: return np.sqrt(15.0/(16.0*np.pi)) * (np.sin(theta)**2) * np.sin(2*phi) # 水素原子の波動関数 Ψ_{n,l,m}(x, y, z) def f(x, y, z, n, l, m, Z_eff): # 座標系を (x,y,z) -> (r,θ,φ) に変換 r = np.sqrt(x*x + y*y + z*z) theta = 0.0 phi = 0.0 if r > 0: theta = np.arccos( z / r ) if y == 0: if x < 0: phi = np.pi elif x*x+y*y > 0: phi = np.sign(y) * np.arccos(x/np.sqrt(x*x+y*y)) # 動径波動関数と球面調和関数の積を計算して出力 return (radial_wave_function(r, n, l, Z_eff) * spherical_harmonics(theta, phi, l, m)) # 水素分子のσ_1s軌道 def hydrogen_molecule(x, y, z, id): Z = 1 # 炭素原子を想定しているので Z = 1 n = 1 l = 0 m = 0 distance = 2.0 # 水素分子の原子核間距離 if id == 0: # σ_1s軌道(結合性軌道) return (f(x-distance/2, y, z, n, l, m, Z)/np.sqrt(3.2)) + (f(x+distance/2, y, z, n, l, m, Z)/np.sqrt(3.2)) else: # σ_1s*軌道(反結合性軌道) return (f(x-distance/2, y, z, n, l, m, Z)/np.sqrt(0.8)) - (f(x+distance/2, y, z, n, l, m, Z)/np.sqrt(0.8)) # エチレン分子のπ_2p軌道 def ethylene_molecule(x, y, z, id): Z = 6 # 炭素原子を想定しているので Z = 6 Z_eff = Z - (0.35*3 + 0.85*2) # 有効核電荷(スレータ―則により計算) n = 2 l = 1 m = 0 distance = 133.9/52.9 # 水素原子のボーア半径 52.9 pm, エチレン分子の原子間距離 133.9 pm if id == 0: # π_2p軌道(結合性軌道) return (f(x-distance/2, y, z, n, l, m, Z_eff)/np.sqrt(2.0)) + (f(x+distance/2, y, z, n, l, m, Z_eff)/np.sqrt(2.0)) else: # π_2p*軌道(反結合性軌道) return (f(x-distance/2, y, z, n, l, m, Z_eff)/np.sqrt(2.0)) - (f(x+distance/2, y, z, n, l, m, Z_eff)/np.sqrt(2.0)) # ブタジエンのπ電子共役系 # http://www.nishino-labo.jp/pdf/enshu01_03_2012.pdf (原子間距離の参考) def butadiene_molecule(x, y, z, id): Z = 6 # 炭素原子を想定しているので Z = 6 Z_eff = Z - (0.35*3 + 0.85*2) # 有効核電荷(スレータ―則により計算) n = 2 l = 1 m = 0 distance_1 = 147.0/52.9 # 水素原子のボーア半径 52.9 pm, C2-C3の原子間距離 147.0 pm distance_2 = 134.0/52.9 # 水素原子のボーア半径 52.9 pm, C1-C2, C3-C4の原子間距離 134.0 pm # 各炭素原子の中心座標 center = [ [0.5 * distance_1 * np.cos(7.0*np.pi/6.0), 0.5 * distance_1 * np.sin(7.0*np.pi/6.0) - distance_2], [0.5 * distance_1 * np.cos(7.0*np.pi/6.0), 0.5 * distance_1 * np.sin(7.0*np.pi/6.0)], [0.5 * distance_1 * np.cos(np.pi/6.0), 0.5 * distance_1 * np.sin(np.pi/6.0)], [0.5 * distance_1 * np.cos(np.pi/6.0), 0.5 * distance_1 * np.sin(np.pi/6.0) + distance_2], ] # 係数 c = [ [0.372, 0.602, 0.602, 0.372], [0.602, 0.372, -0.372, -0.602], [0.602, -0.372, -0.372, 0.602], [-0.372, 0.602, -0.602, 0.372], ] res = 0.0 for i in range(4): x0 = x - center[i][0] y0 = y - center[i][1] res += f(x0, y0, z, n, l, m, Z_eff) * c[id][i] return res # ベンゼン分子のπ電子共役系 def benzene_molecule(x, y, z, id): Z = 6 # 炭素原子を想定しているので Z = 6 Z_eff = Z - (0.35*3 + 0.85*2) # 有効核電荷(スレータ―則により計算) n = 2 l = 1 m = 0 distance = 139/52.9 # 水素原子のボーア半径 52.9 pm, ベンゼン分子の炭素間距離 139 pm # 各炭素原子の中心座標 center = [] for i in range(6): cx = distance * np.sin(2*i*np.pi/6) cy = distance * np.cos(2*i*np.pi/6) center.append([cx,cy]) # 係数 c = [ [1/np.sqrt(6), 1/np.sqrt(6), 1/np.sqrt(6), 1/np.sqrt(6), 1/np.sqrt(6), 1/np.sqrt(6)], [1/np.sqrt(3), 1/(2.0*np.sqrt(3)), -1/(2.0*np.sqrt(3)), -1/np.sqrt(3), -1/(2.0*np.sqrt(3)), 1/(2.0*np.sqrt(3))], [0.0, 1/2.0, 1/2.0, 0.0, -1/2.0, -1/2.0], [1/np.sqrt(3), -1/(2.0*np.sqrt(3)), -1/(2.0*np.sqrt(3)), 1/np.sqrt(3), -1/(2.0*np.sqrt(3)), -1/(2.0*np.sqrt(3))], [0.0, 1/2.0, -1/2.0, 0.0, 1/2.0, -1/2.0], [1/np.sqrt(6), -1/np.sqrt(6), 1/np.sqrt(6), -1/np.sqrt(6), 1/np.sqrt(6), -1/np.sqrt(6)], ] res = 0.0 for i in range(6): x0 = x - center[i][0] y0 = y - center[i][1] res += f(x0, y0, z, n, l, m, Z_eff) * c[id][i] return res # サンプリングの設定 N = 50 # サンプリング個数 x_range = 5 # 座標の範囲 (-x_range, x_range) delta = 2.0*x_range / N # サンプリング間隔 #print(delta) # 3次元空間を格子状にサンプリング(間隔 delta, N^3 個) data_list = [] for i in range(N): for j in range(N): for k in range(N): x = i*delta - x_range y = j*delta - x_range z = k*delta - x_range # 座標 (x,y,z) における波動関数 Ψ(x,y,z) を計算 # psi = hydrogen_molecule(x,y,z, 0) # id = 0 or 1 # psi = ethylene_molecule(x,y,z, 1) # id = 0 or 1 # psi = butadiene_molecule(x,y,z, 0) # id = 0, 1, 2, 3 psi = benzene_molecule(x,y,z, 0) # id = 0, 1, 2, 3, 4, 5 # 波動関数の2乗によって電子の確率密度関数 |Ψ(x,y,z)|^2 を計算 pdf = psi**2 # 確率密度(|Ψ(x,y,z)|^2, p.d.f), x, y, z, 波動関数の生の値 Ψ(x,y,z) の順にデータを格納 data_list.append([pdf, x, y, z, psi]) # 確率密度が高い順にサンプリングデータをソートする sorted_list = sorted(data_list, key=lambda data: data[0], reverse=True) # 確率密度(p.d.f)でソート # 波動関数が正のデータを格納する変数 x1_list = [] y1_list = [] z1_list = [] # 波動関数が負のデータを格納する変数 x2_list = [] y2_list = [] z2_list = [] # 現在考えている全体の空間(体積: (x_range)^3)における積分値を計算しておく(あとで使う) def integral_in_all_spaces(): integral = 0.0 i = 0 while i < len(sorted_list): pdf = sorted_list[i][0] psi = sorted_list[i][4] # |Ψ(x,y,z)|^2 ΔV を加算 integral += (pdf * delta**3) i += 1 print("グリッド数: {}, 全空間の積分: {}".format(i, integral) ) return integral all_integral = integral_in_all_spaces() # |Ψ|^2 ΔV の総和( volume )が 0.9 を超えるまで足し合わせる(体積が0.9を超えたら終了) integral = 0.0 i = 0 while integral < 0.9 * all_integral: # 全空間の積分値に対して 90 % になる領域を描画するように変更 pdf = sorted_list[i][0] x = sorted_list[i][1] y = sorted_list[i][2] z = sorted_list[i][3] psi = sorted_list[i][4] # |Ψ(x,y,z)|^2 ΔV を加算 integral += (pdf * delta**3) if psi > 0: x1_list.append(x) y1_list.append(y) z1_list.append(z) else: x2_list.append(x) y2_list.append(y) z2_list.append(z) i += 1 # figureを生成する X1 = np.array(x1_list) Y1 = np.array(y1_list) Z1 = np.array(z1_list) X2 = np.array(x2_list) Y2 = np.array(y2_list) Z2 = np.array(z2_list) #''' # matplotlibによる可視化 fig = plt.figure(figsize=(8.0, 8.0)) ax = fig.add_subplot(1,1,1, projection='3d') ax.set_xlim3d(-x_range, x_range) ax.set_ylim3d(-x_range, x_range) ax.set_zlim3d(-x_range, x_range) # 軸の設定 ax.set_xlabel("x", size = 14) ax.set_ylabel("y", size = 14) ax.set_zlabel("z", size = 14) ax.plot(X2,Y2,Z2,color='b',marker="o",linestyle='None') ax.plot(X1,Y1,Z1,color='r',marker="o",linestyle='None') plt.show() #''' ''' # Plotlyによる可視化 import plotly.graph_objects as go fig = go.Figure(data=[go.Scatter3d( x = X1, y = Y1, z = Z1, mode='markers', marker = dict( size = 2, color = 'red' ) ), go.Scatter3d( x = X2, y = Y2, z = Z2, mode='markers', marker = dict( size = 2, color = 'blue' ) )]) fig.update_layout( scene = dict( camera=dict(eye=dict(x=1.7, y=-1.7, z=1.7)), #eye=dict(x=1.25, y=1.25, z=1.25)), xaxis = dict(range=[-x_range, x_range]), yaxis = dict(range=[-x_range, x_range]), zaxis = dict(range=[-x_range, x_range]), aspectmode='cube', #this string can be 'data', 'cube', 'auto', 'manual' #a custom aspectratio is defined as follows: aspectratio=dict(x=1, y=1, z=0.95) ), width=800, height=700, ) fig.show() '''
プログラム内の次の箇所を変えると(コメントアウトを変更すると)、表示する分子軌道の種類を変えることができます。(デフォルトはベンゼンの 軌道。)
# 座標 (x,y,z) における波動関数 Ψ(x,y,z) を計算 # psi = hydrogen_molecule(x,y,z, 0) # id = 0 or 1 # psi = ethylene_molecule(x,y,z, 1) # id = 0 or 1 # psi = butadiene_molecule(x,y,z, 0) # id = 0, 1, 2, 3 psi = benzene_molecule(x,y,z, 0) # id = 0, 1, 2, 3, 4, 5
また、デフォルトでは、matplotlibで描画するようになっていますが、matplotlibの箇所をコメントアウトして、コメントアウトされているplotlyの箇所を戻せばplotlyで可視化できます。(plotlyを使用する際には、plotlyのインストールが別途必要です。)
9. おわりに
今回は分子軌道論を解説し、分子軌道を実際に計算するPythonプログラムを紹介しました。
実際にプログラムを使って描くことができると感動します。可視化の過程で理論の理解も深まると思います。理屈が分かると、化学の教科書の説明も納得できて、とても楽しい!
ブタジエンの例では、分子軌道において電子が占有されている最高エネルギーの軌道(HOMO)と、電子が空である最低エネルギーの軌道(LUMO)について紹介しました。そして、HOMO-LUMO間のエネルギー差によって、分子が吸収する波長が変わること、そしてそれが物質の「色」に関係するということでした。
次回は、日曜化学シリーズ(おそらく)最終回として、特にこの「色」について考えたいと思います。
だいぶ長い記事でしたが最後まで読んでいただきありがとうございました!
それでは今日はこの辺で!
