今回の記事は「シリーズ:連分数とペル方程式」の1日目の記事となっています。関連する記事は こちら からご覧いただけます。
今日は、連分数展開 について紹介したいと思います。
3日連続 で 「連分数」 に関連する記事を公開したいと思っています。明日以降の記事の準備として、以下の3つのトピックを紹介したいと思います:
- 連分数展開を計算するためのウェブアプリの紹介
- 連分数展開の計算方法の紹介(2通り)
- 連分数を用いた無理数の近似
連分数とは
という形に、分数が入れ子になった構造の分数のことを指します。
特に、各分子の数列 がすべて
であるものを正則連分数といいます。
今回の記事では、正則連分数のみを扱いたいと思います。正則連分数は
のように表すことができます。
また、分数の入れ子を無限に繰り返すことで
なるものを考えることができ、これも連分数ということにします。(特に、分子が であるものを正則連分数といいます。)
与えられた数が連分数の形で表せるかどうかは気になるところですが、重要な事実として 任意の実数は必ず連分数の形で表すことができます 。
実数 を式
の形で表すことを
の連分数展開 といいます。
たとえば の場合は
のように正則連分数に展開できます。式 の分母の数列がそれぞれ
というわけですね。
今日は、実数(特に という形の無理数)の連分数展開を計算する方法を 2通り 紹介したいと思います。2通りといいつつ、基本的な考え方はどちらも同じです。
宣伝:連分数を計算するアプリを作りました!
計算方法の紹介の前に、今回のために作成した自作アプリの紹介をさせてください!
これから連分数展開の計算を行うのですが、実際やってみると手順が込み入っていて、計算するのはなかなか大変です。そこで、計算結果をすぐに調べることができるよう の連分数展開を計算してくれるアプリ を作りました。
tsujimotter.info
使い方は簡単です。
たとえば、、
と入力して「計算」ボタンを押すと、
の連分数展開を
項目(
)まで計算してくれます:
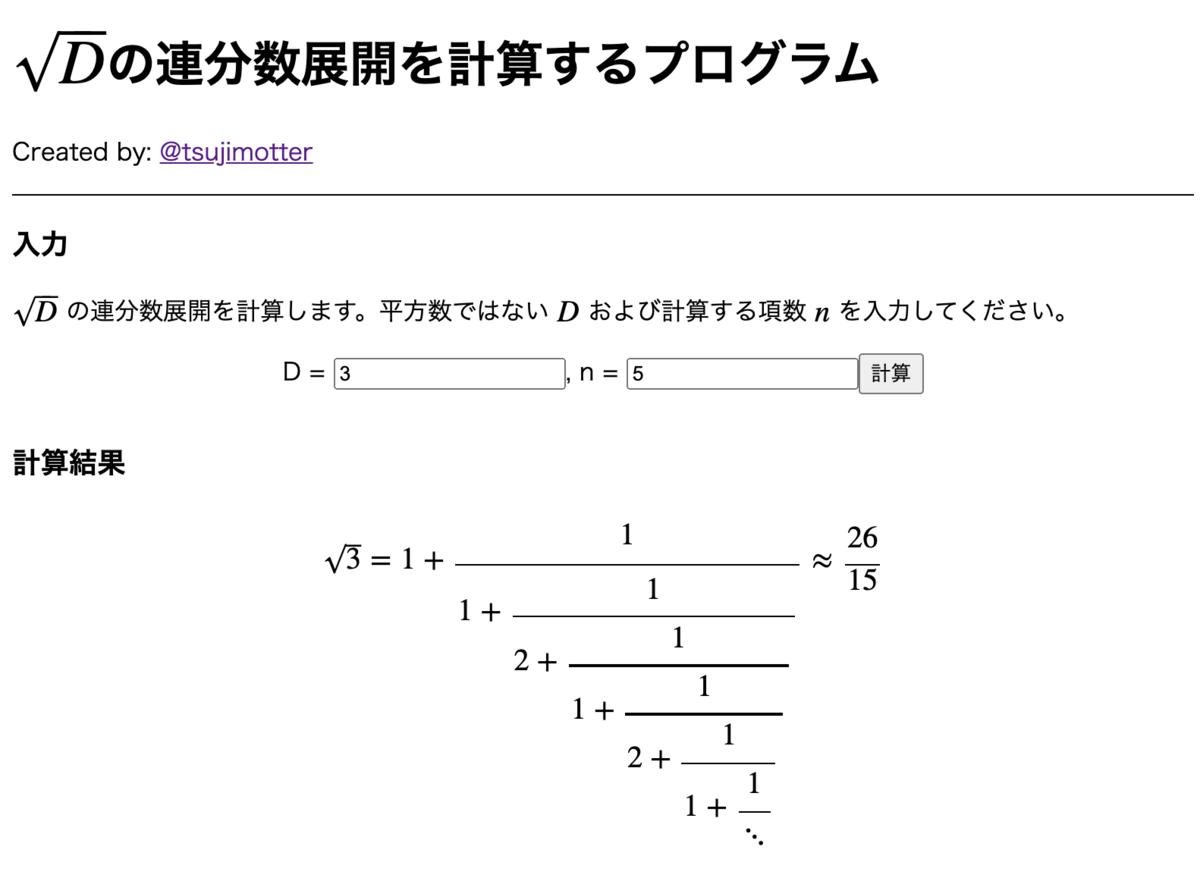
あとで説明するように、 項目までの近似分数も計算してくれます。LaTeXのテキストも一緒に出力してくれるので、ブログに貼り付けたりすることも簡単にできます。
計算が面倒なときに使ったり、手計算の験算に使ったり、ぜひご活用いただけると嬉しいです!
なお、連分数の計算アルゴリズムは、こちらのサイトの記事を参考にさせていただきました。
parametron.blogspot.com
それでは、計算方法の紹介にいきましょう!
連分数展開の計算方法①:小数展開を用いる方法
まずは、小数展開を用いた方法を紹介したいと思います。手元に電卓がある方は、一緒に計算してみてください。
なお、電卓を使う際に、必要な操作は「引き算」「√」「逆数をとる」の3つとなります。いずれのボタンもあると楽に計算できます。
逆数については、そのようなボタンがないことが多いです。しかしながら、たとえばシャープの電卓では「÷=」、カシオの電卓では「÷÷」を押すことで逆数を計算できるそうです。
pro-boki.com
まず、 を小数展開します。電卓では
を入力したあと「√」ボタンを押すとよいでしょう。
1. 整数部分をとる:
上の数の整数部分をとると となります。これを覚えておきます(どこかにメモする)。計算結果から整数部分
を引いてみてください。すると、残った小数部分は
となりますね。
2. 小数部分の逆数をとる:
小数部分は 以上
未満の数となります。これの逆数をとると
となります。
3. 2. の整数部分をとる:
上の数の整数部分をとると となります(これもメモを取るか覚えておいてください)。小数部分は
となります。
4. 小数部分の逆数をとる:
再度逆数をとると
となります。
5. 4. の整数部分をとる:
整数部分をとると となります(これもメモを取るか覚えておいてください)。
こんな風に繰り返していくことで、 の連分数展開を得ることができます。
まとめると、 を小数展開して、以下の手順を実行すれば良いわけですね。
- 1. 整数部分をとる(
)
- 2. 小数部分の逆数をとる
- 3. 2. の整数部分をとる(
)
- 4. 小数部分の逆数をとる
- 5. 4. の整数部分をとる(
)
以上を繰り返す。
ところで、上の手順5.で整数部分をとった後、残った数は
となりました。この数にピンときた方はいますでしょうか。
実はこれは の小数部分となっているのです。すなわち、ここから先はずっと同じ計算になります。
の周期が繰り返されるというわけです。
一般に を平方数ではない数としたとき、
の正則連分数展開は循環する ことが知られています。そのため、計算していくなかで元々の小数展開が現れた時点で計算を終了して良いわけですね。
ただし、循環周期の長さを決定する上で、①の方法には注意点があります。それは予め十分な長さの桁数を取って、小数展開をしなければならないということです。ステップを進めるたびに小数の有効桁数が減っていきますので、最初に十分な桁数を取っておかないと、途中で結果がおかしくなってしまうのですね。
この問題を回避するために、小数展開をせず直接計算するというのが②の方法です。
連分数展開の計算方法②:直接計算する方法
先ほどは小数に展開してから連分数を計算しましたが、循環するかどうかが厳密に評価できないという問題がありました。そこで今度は、上とまったく同じ手順を「 を小数展開せずに(
をそのまま残しつつ)」実行する方法を紹介します。これによって、循環するポイントを厳密に評価できます。
今回は電卓は基本的に使えないので、手計算でがんばりましょう。
1. 整数部分をとる:
の整数部分をとると
となります。
は
の整数部分を取り出す記号です(小数点以下を切り捨てと思ってもいいです)。
整数部分をとる操作については小数展開を用いてもいいですし、 となる整数
を探しても良いです。
2. 小数部分の逆数をとる:
整数部分を取り除いた小数部分は、 から
を引いて
となりますが、これは 以上
未満の数となります。これの逆数をとると
となります。
3. 2. の整数部分をとる:
整数部分をとると となります。この部分の計算は、一旦分数を有理化して
結果の整数部分 をとればよいでしょう。この計算もやはり
の小数展開が必要そうに見えるかもしれませんが、必要なのは
の整数部分だけです。
なので
が得られます。
4. 小数部分の逆数をとる:
から
を引くと、
の小数部分が得られます:
再度逆数をとると
となります。
5. 4. の整数部分をとる:
の整数部分
を計算します。やはり有理化すると
となりますが、 より、整数部分は
となります。
こんな風に繰り返していけばいいわけですね。
ここで、最後の結果から整数部分を除いた小数部分は
となることに気づきます。これは手順2. に登場した結果と等しいので、ここから先は同じ計算が繰り返されるというわけですね。
今回の場合は、 をそのまま残しているので、厳密に循環することが評価できていることに注意しましょう。ただし、手計算でないと実行できないことと、循環周期が長くなると計算が煩雑になるという問題があります。また、
以外の無理数だと、この方法はなかなか難しいかもしれません。良し悪しですね。
なお、最初に紹介したアプリは、基本的にはこの②の方法を使っています。したがって、 の計算は厳密に実行できています。なので、計算が大変だと思ったら、どんどんアプリを使っちゃってください。
連分数を用いた無理数の近似
最後に、連分数展開の面白い応用を一つ紹介します。それは無理数の精度の高い 近似分数 を得ることです。
まず、連分数展開の近似分数を定義したいと思います。ある無理数 が
と表せるとき、この右辺を 項目の
までで打ち切って得られる分数
を、 の近似分数と呼びます。(
次の近似分数と言ったりもします。)
近似分数は、分数の計算を順次実行していくことで、分数 の形にすることができます。これは有理数なので、つまり近似分数とは無理数を有理数に近似する操作ということになりますね。
もちろん、分数の計算を順次実行していっても良いのですが、これは結構手間なことが多いです。近似分数を計算するには、以下の漸化式が便利です:
が与えられたとき、次の漸化式が成り立つ:
この方法のよいところは前から順に機械的に計算できることですね。普通、上記の連分数を計算しようと思ったら、 と
を足すところから始めると思います。 上の方法では、
の方から計算することができ、自然な順序で計算できるのがポイントです。
三項間漸化式なので、フィボナッチ数列と同じ要領で計算することができます。実際、 のときはフィボナッチ数列そのものになりますので、以下の連分数はフィボナッチ数の比
の極限となります。すなわち、黄金比
の連分数展開ですね:
また、漸化式を観察すると、分母と分子が独立に計算できることがわかります。したがって、分母だけの評価をしたいときにも有効です。
さて、 の近似分数を求めてみましょう。
(
との誤差:
)
(
との誤差:
)
(
との誤差:
)
(
との誤差:
)
(
との誤差:
)
(
との誤差:
)
こんな風に、だんだんと良い精度の近似分数が得られます。
面白い例を紹介すると、アルキメデスが円周率を計算する際に使った
という近似があるのですが、これは の連分数展開の
次近似分数となっています。
このときの との誤差は
となります。かなり小さいですね。
tsujimotter.hatenablog.com
連分数展開の近似分数の著しい性質として、分母の大きさに対して 最良近似 を与えるというものがあります。
連分数展開による無理数 の近似分数が
であるとき、これより分母の小さい分数であって、
より誤差の小さい分数は存在しないということです。このような性質を最良近似といいます。
の例でいうと、分母が
より小さい分数であって、
との誤差が
未満になるものは存在しないということですね。
実際、分母 を固定したとき、誤差
が最も小さくなるような分子
を選ぶことにします。このとき、横軸
に対して縦軸
をプロットすると、次のようなグラフが描けます:
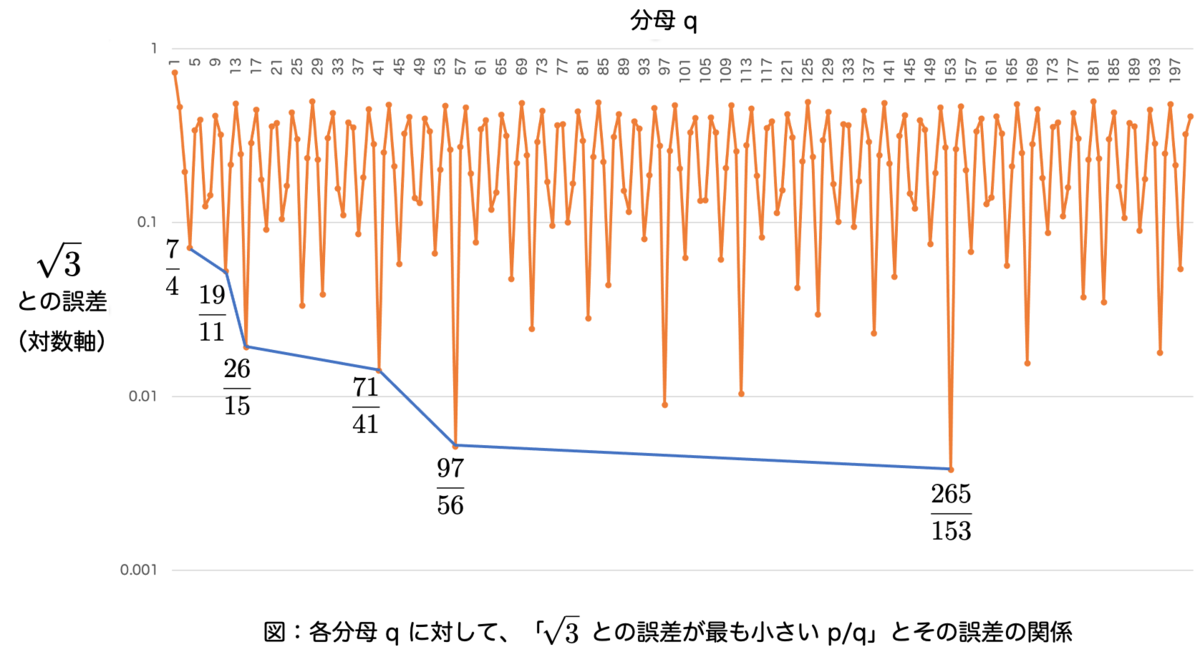
グラフを見ると、最良近似の誤差が更新されるタイミングはすべて連分数展開の近似分数になっていることが確認できます。面白いですね!
以前書いたように、円周率の有名な近似分数 は、円周率の正則連分数展開の近似分数になっています。これらの近似分数の精度の良さも、上とまったく同じ理屈で説明することができます。
tsujimotter.hatenablog.com
そんなわけで、連分数展開は無理数の近似を行うのに有効だというのが今回のまとめです。
近似分数の計算については、アプリの方でも自動で実行してくれますので、こちらをご活用ください。計算結果の右側に出てくるのが、 次の近似分数
となっています。
tsujimotter.info
今日は連分数の計算方法と近似分数の有効性について紹介しましたが、明日は連分数の整数論的な応用を紹介したいと思います!お楽しみに!
それでは今日はこの辺で!
