1/512の有限小数と冪零元 - tsujimotterのノートブック

今日は5月12日なので 512 の日ですね！

$512 = 2^9$ なので、2のべき乗で表せる数というわけです！嬉しいですね！（え、嬉しくないですか？）

楽しくなってきたので他にも面白い性質ないかなと、Wikipediaの「512」という項目を調べてみると、次のような性質を見つけました。

$2^i \times 5^j$ （ $i\geq 0, \; j \geq 0$ ）で表せる24番目の数である。1つ前は500、次は625。(オンライン整数列大辞典の数列 A003592)

なるほど

$512 = 2^9 \times 5^0$

と書けるので、 $2^i \times 5^j$ で表せる数ということですね。

・・・ $5$ 関係ないですやん。

この性質に何の意味があるんだろう・・・。このWikipediaの記事を書いた人は、どういう気持ちでこの性質を追加したのだろう・・・。

このままでは512がかわいそうなので（？）、 $2^i \times 5^j$ で表せる数に何か数学的な意味を見出してあげたいですね。

そこで私が思いついたのは

$\displaystyle \frac{1}{512}$

という分数についてです。

計算してみると

$\displaystyle \frac{1}{512} = 0.001953125$

となりますが、これは小数点以下９桁でストップする小数となります。つまり、有限小数というわけですね。

実際、筆算を計算してみると

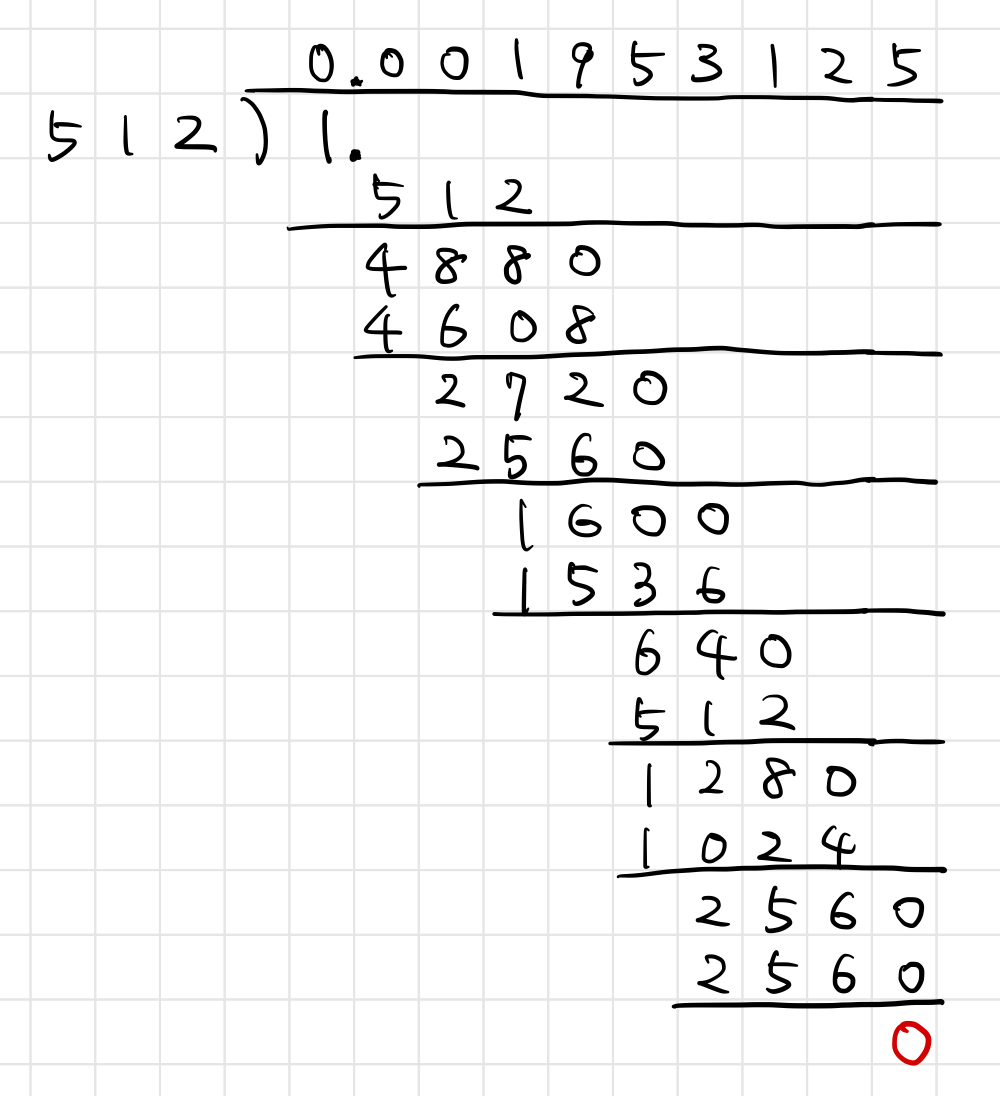
f:id:tsujimotter:20210512130209j:plain:w300

となって、小数第９位を計算するとあまりが０になり、小数がそこでストップするというわけです。

これは小数点を取り払って

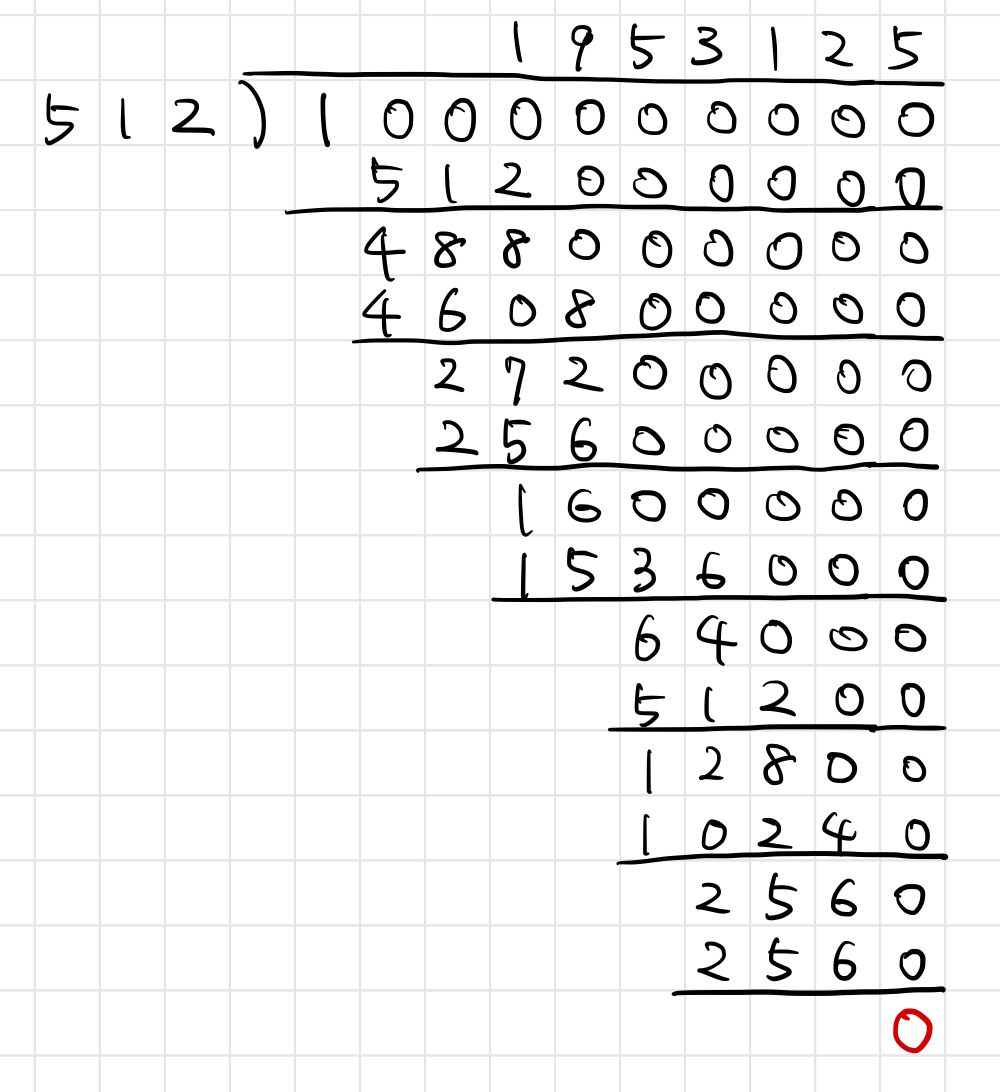
f:id:tsujimotter:20210512155333j:plain:w300

という割り算を計算していることに他なりません。

つまり

$1000000000$ が $512$ でちょうど割り切れる

ということになりますね。

一般に、

$10^n$ が $m$ でちょうど割り切れる

ような $n > 0$ が存在するときに、 $1/m$ は10進法で有限小数になります。

たいていの $m$ においては $1/m$ は有限小数にはならず、循環する無限小数になります。

たとえば、 $1/3$ については

$\displaystyle \frac{1}{3} = 0.333333333\ldots$

ですし、 $1/7$ についても

$\displaystyle \frac{1}{7} = 0.142857142857\ldots$

のように、循環しながら無限に続いていくわけです。

実は、 $m = 2^i \times 5^j$ （ $i\geq 0, \; j\geq 0$ ）と表せるときに限り、 $1/m$ は10進法で有限小数となります。

$512$ も $2^9 \times 5^0$ と書けるので、有限小数となるわけですね。

そんなわけで、上の $512$ の性質に意味づけができました。
（もちろんこれは単なるこじつけであって、元々のWikipediaの執筆者さんの意図は違うものだと思います。）

有限小数と冪零性

さらに突っ込んで考えてみましょう。「 $1/(2^i 5^j)$ が10進法で有限小数になる」という理屈について考えたいと思います。

先ほどと同様に考えて

$10^n$ が $m = 2^i 5^j$ で割り切れる

なる $n > 0$ が存在するとき、 $1/m$ が10進法で有限小数になります。そうでないとき有限小数にはならない（循環小数になる）、ということになります。

ここで

$10^n$ が $m = 2^i 5^j$ で割り切れる

という条件は、合同式を用いて

$10^n \equiv 0 \pmod{m}$ （ただし、 $m = 2^i 5^j$ ）

と言い換えられます。

環論的にいうと $m = 2^i 5^j$ についての環 $\mathbb{Z}/m\mathbb{Z}$ において、 $\overline{10}$ という元に対して

$\overline{10}^n = \overline{0}$

なる $n > 0$ が存在する、ということです。このような性質を持つ $\overline{10}$ のような元のことを冪零元（べきれいげん）といいます。

より一般に冪零元は次のように定義されます。

$R$ を可換環とする。 $x \in R$ に対して

$x^n = 0$

を満たす $n > 0$ が存在するとき、 $x$ は冪零元であるという。

つまり、 $1/m$ が有限小数かどうかという問題は、可換環 $R = \mathbb{Z}/m\mathbb{Z}$ において、 $\overline{10}$ が冪零元かどうかで決まる、ということになりますね。

可換環 $R = \mathbb{Z}/m\mathbb{Z}$ において

$\overline{10}$ が冪零元 $\;\; \Longleftrightarrow \;\;$ $1/m$ が10進法で有限小数

ここで、 $m = 2^i 5^j$ において、 $\overline{10}$ が冪零元になるのは簡単にわかります。 $n$ として $i$ と $j$ のうち大きい方をとれば

$10^n = 2^n \times 5^n$

となり、これが $2^i \times 2^j$ で割り切れるからです。

一般に、 $x \in \mathbb{Z}/m\mathbb{Z}$ が「 $m$ を割り切る素数すべてによって割り切れる」のであれば、 $x$ は冪零元ということになります。

逆に、 $m$ を割り切る素数 $p$ であって、 $x$ を割り切らない $p$ が一つでも存在するのであれば、 $x$ は冪零ではなくなってしまうというわけですね。

$10$ を割り切る素数は $2$ と $5$ だけですから、 $1/m$ が10進法で有限小数になるのは $m = 2^i \times 5^j$ という形に限られるということになります。

冪零根基との関係

以上で、 $1/m$ が有限小数になる $m$ の必要十分条件が得られましたので、ここで終わりにしてもいいぐらいです。しかし、せっかく可換環論的な話題になりましたので、もう一つ別の見方が与えられそうだと思いました。

可換環 $R$ のイデアル $I$ があったときに

$\sqrt{I} = \{ x \in R \; \mid \; \exists n > 0 , \; x^n \in I \}$

で定義される集合 $\sqrt{I}$ をイデアル $I$ の根基といいます。特に $I = (0)$ に対する根基 $\sqrt{(0)}$ を冪零根基といいます。

冪零根基は、要するに $R$ 内の冪零元全体の集合ということになります。よって「 $1/m$ が有限小数か」という問題は「 $R = \mathbb{Z}/m\mathbb{Z}$ において $\overline{10} \in \sqrt{(0)}$ か」という問題に言い換えられます。

実は $\sqrt{I}$ 自身は、単なる集合ではなく $R$ のイデアルでもあることがわかります。

$\sqrt{I} \neq \emptyset$ が $R$ のイデアルであることを示すためには、次の①②を言えば良いことになります：

① $x, y \in \sqrt{I} \;\; \Longrightarrow \;\; x+y \in \sqrt{I}$
② $x \in \sqrt{I}, \; r \in R \;\; \Longrightarrow \;\; rx \in \sqrt{I}$

実際イデアルの条件①について、 $x, y \in \sqrt{I}$ とすると、ある $k, l > 0$ が存在して

$x^k \in I, \;\; y^l \in I$

ということになります。ここで二項定理により

$(x+y)^{k+l} = x^{k+l} + \binom{k+l}{1} x^{k+l-1}y + \cdots + \binom{k+l}{i} x^i y^{k+l-i} + \cdots + \binom{k+l}{k+l-1}xy^{k+l-1} + y^{k+l}$

となりますが、 $x^i$ か $y^{k+l-i}$ のどちらかは $x^k$ または $y^l$ で割り切れるので、全体として $(x+y)^{k+l} \in I$ です。つまり $x+y \in \sqrt{I}$ です。

こんなところで二項定理が使えるというのが面白いですね。

また、イデアルの条件②については、 $x \in \sqrt{I}, \; r \in R$ とすると、ある $k > 0$ が存在して

$x^k \in I$

ということになり、 $I$ はイデアルより $(rx)^k = r^k x^k \in I$ ですから $rx \in \sqrt{I}$ ということになります。

さらに、 $\sqrt{(0)}$ は、 $R$ のすべての素イデアルの交叉を用いて

$\displaystyle \sqrt{(0)} = \bigcap_{\mathfrak{p} \subset R} \mathfrak{p}$

のように表せることが知られています。

$\sqrt{(0)} \subset \bigcap_{\mathfrak{p} \subset R} \mathfrak{p}$ であることは簡単に示せますので、ここでやってみましょう。

$x \in \sqrt{(0)}$ であるとすると、 $x^n = 0$ なる $n > 0$ が存在するということになります。

一方、 $\mathfrak{p}$ を $R$ の任意の素イデアルとすると $0 \in \mathfrak{p}$ となります。つまり $x^n \in \mathfrak{p}$ ということですね。

素イデアルの定義より $x^n \in \mathfrak{p}$ ならば $x \in \mathfrak{p}$ ということになりますから、 $x \in \bigcap_{\mathfrak{p} \subset R} \mathfrak{p}$ が示されます。

逆の $\sqrt{(0)} \supset \bigcap_{\mathfrak{p} \subset R} \mathfrak{p}$ も環の局所化を使って証明できるそうなのですが、まだちゃんと理解できていないのでここでは省略させてください。（参考文献の３番目の動画参照）

結局何が言いたいかというと、冪零元全体は素イデアルの共通部分をとることで特定できるということですね。

ここで、 $R = \mathbb{Z}/m\mathbb{Z}$ の素イデアル全体を考えたいと思います。 $R = \mathbb{Z}/m\mathbb{Z}$ 自身は、 $R' = \mathbb{Z}$ のイデアル $I' = m\mathbb{Z}$ による剰余環 $R' / I'$ に他なりません。

剰余環 $R = \mathbb{Z}/m\mathbb{Z}$ の素イデアルは、 $R' = \mathbb{Z}$ における $I' = m\mathbb{Z}$ を含む素イデアル全体と１対１に対応します。 $R'$ の素イデアルは $(0)$ または素数 $p$ を用いて $(p)$ と表せますから、結局 $m$ を割り切る素数に対する $(p)$ が $\mathbb{Z}/m\mathbb{Z}$ の素イデアル全体ということになります。