今日のテーマは 「リーマンの再配列定理」 です。「条件収束する実数列の級数は、再配列によって任意の実数に収束させることができる」という主張です。何を言っているかわからないという方にも、これから詳しくは説明していきますのでご安心ください。
無限級数
が絶対収束するとは、各数列に絶対値をつけた
が収束するということです。名前の通りですね。
対する条件収束とは、無限級数が絶対収束はしないが収束はすることを言います。
たとえば、平方数の逆数の和
は絶対収束しますが、自然数の逆数を足し引きする級数(交代級数)
は条件収束します。
「なぜ絶対収束か条件収束を気にするのか」と疑問に思った方もいるかもしれませんが、それにはワケがあります。
絶対収束する級数は、足し合わせる順番に関わらず同じ値に収束します。つまり、足し合わせる順番を気にする必要がないわけですね。
一方、条件収束する級数については、足し合わせる順番によって収束する先の値が変わってしまう のです。条件収束はとてもナイーブなのですね。
たとえば、 に収束する式
の級数ですが、足し合わせる順番を入れ替えて
のように和をとると、 に収束してしまいます。(計算は自分で確かめてみるといいでしょう。)
さらに面白いことに、冒頭の「リーマンの再配列定理」によれば、条件収束する級数は(足し合わせる順番を入れ替えることで)任意の実数値に収束させることができる というのです。
これはなんというか、とても非自明な感じがしますよね。なんたって任意の実数値ですから。
正確な主張と証明は、以下の記事にまとまっています。
integers.hatenablog.com
とにかく証明はできるわけです。tsujimotterはこれまで証明をきちんと追ったことがなく、なんとなくよくわからないな、難しそうだなとモヤモヤしていました。
そろそろちゃんと理解したいなと思い、つい先ほど証明を追いかけてみたのですが、思っていたよりスッキリ理解することができました。しかも、よくよく読んでみると、証明の中に任意の実数値に収束させる方法が載っていることに気づきました。
これは面白いかもしれない! なんたって、好きな実数に収束させることができるのですから!
そんなわけでイントロが長くなりましたが、本日の記事では 条件収束する級数をお望みの実数に収束させる手順 を紹介したいと思います。
お望みの実数に収束させる手順
(用意するもの)
- 条件収束する級数(1個):
ただし、
- 収束させたい実数値(お好みで):
(手順)
- ①数列
を「正のものだけを集めた数列」と「負のものだけを集めた数列」に分けます。
- ※条件収束の仮定より、どちらの級数も発散することがわかります。
- ②「正のものだけを集めた数列」だけを使って、総和が
をちょうど超えるまで足し合わせる。
- ※発散級数なので、任意の実数に対して、それを超える有限の部分和が存在します。
- ③「負のものだけを集めた数列」だけを使って、総和が
をちょうど下回るまで足し合わせる。
- ④「正のものだけを集めた数列」の残りの数列を使って、再度総和が
をちょうど超えるまで足し合わせる。
- ⑤ 「負のものだけを集めた数列」の残りの数列を使って、再度総和が
をちょうど下回るまで足し合わせる。
- ⑥以下、④と⑤を繰り返す。
たったこれだけです。
たしかに、この手順であれば実数 に収束させることができますね。
(詳しい証明は上記の記事を参照)
交代級数をお望みの実数に
それでは上記の手順を具体的に実行してみましょう。
実験台はもちろん交代級数です:
具体例として、順番を入れ替えて に収束させてみましょう。
①「正のものだけを集めた数列」
と「負のものだけを集めた数列」
に分けます。
②「正のものだけを集めた数列」を使って、 をちょうど超えるまで足し合わせてみましょう。実際
まで足し合わせると
を超えることがわかります:
③「負のものだけを集めた数列」を使って、 をちょうど下回るまで足し合わせてみましょう。実際
を足すだけで
を下回ります:
④「正のものだけを集めた数列」の残りの数列を使って、再度総和が をちょうど超えるまで足し合わせましょう:
⑤「負のものだけを集めた数列」の残りの数列を使って、再度総和が をちょうど下回るまで足し合わせましょう:
⑥以下、④と⑤を繰り返します。すると、 に収束する級数が得られます:
面白いですね!
収束の様子をグラフにすると次のようになります:
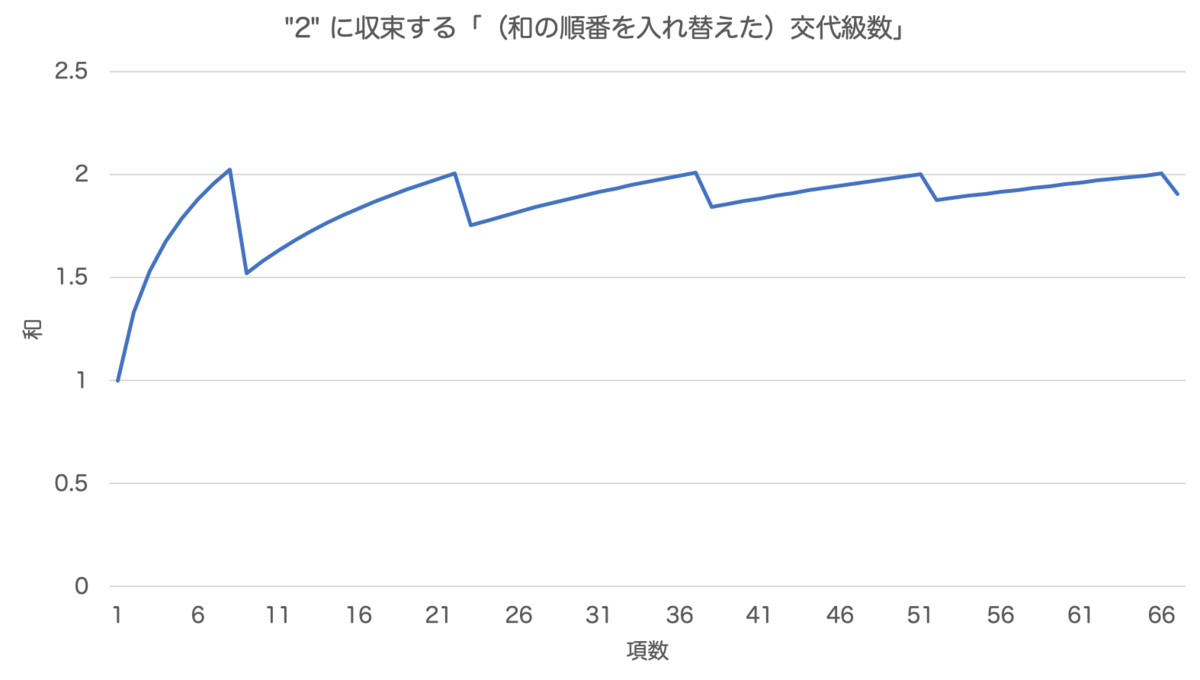
同様に 円周率 に収束する(和の順番を入れ替えた)交代級数は次のようになります:
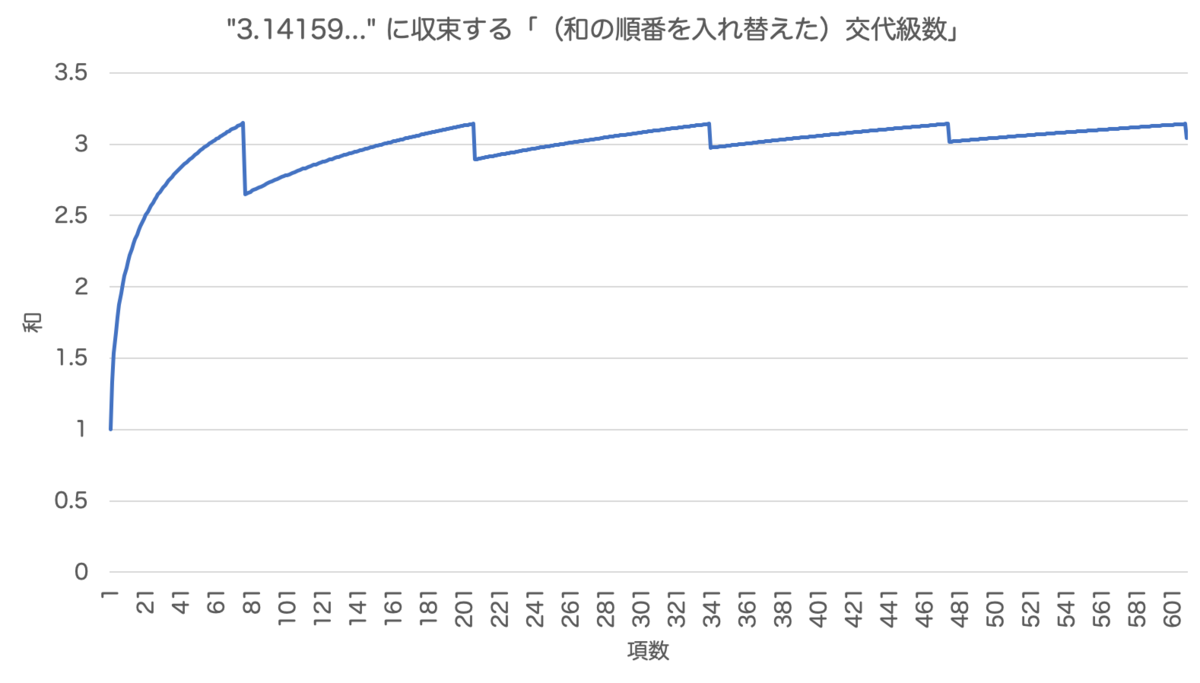
ちゃんと に収束しそうですね!
原理的には、 だろうが 5000兆 であろうが、好きな実数値に収束させることができるというわけです。
検証用のPythonコードは次の通りです。よろしければ遊んでみてください:
r = 3.14159265 # 【収束させたい先の実数値をここに入れる】 #r = 2 # 【収束させたい先の実数値をここに入れる】 def a_pos(n_pos): return 1/(2*n_pos+1) def a_neg(n_neg): return -1/(2*n_neg+2) n_pos = 0 n_neg = 0 sum = 0 pos_neg_flag = 1 # 1: pos, -1: neg for i in range(5): print("(ans) ".format(2*n_pos+1), end='') if pos_neg_flag > 0: while sum < r: sum += a_pos(n_pos) #print(sum) print("+ 1/{}".format(2*n_pos+1), end='') n_pos += 1 else: while sum > r: sum += a_neg(n_neg) #print(sum) print("- 1/{}".format(2*n_neg+2), end='') n_neg += 1 print(" =",sum) pos_neg_flag *= -1 # pos, neg を反転
実行してみると、こんな感じになります:
(ans) + 1/1+ 1/3+ 1/5+ 1/7+ 1/9+ 1/11+ 1/13+ 1/15+ 1/17+ 1/19+ 1/21+ 1/23+ 1/25+ 1/27+ 1/29+ 1/31+ 1/33+ 1/35+ 1/37+ 1/39+ 1/41+ 1/43+ 1/45+ 1/47+ 1/49+ 1/51+ 1/53+ 1/55+ 1/57+ 1/59+ 1/61+ 1/63+ 1/65+ 1/67+ 1/69+ 1/71+ 1/73+ 1/75+ 1/77+ 1/79+ 1/81+ 1/83+ 1/85+ 1/87+ 1/89+ 1/91+ 1/93+ 1/95+ 1/97+ 1/99+ 1/101+ 1/103+ 1/105+ 1/107+ 1/109+ 1/111+ 1/113+ 1/115+ 1/117+ 1/119+ 1/121+ 1/123+ 1/125+ 1/127+ 1/129+ 1/131+ 1/133+ 1/135+ 1/137+ 1/139+ 1/141+ 1/143+ 1/145+ 1/147+ 1/149+ 1/151 = 3.147125289923645 (ans) - 1/2 = 2.647125289923645 (ans) + 1/153+ 1/155+ 1/157+ 1/159+ 1/161+ 1/163+ 1/165+ 1/167+ 1/169+ 1/171+ 1/173+ 1/175+ 1/177+ 1/179+ 1/181+ 1/183+ 1/185+ 1/187+ 1/189+ 1/191+ 1/193+ 1/195+ 1/197+ 1/199+ 1/201+ 1/203+ 1/205+ 1/207+ 1/209+ 1/211+ 1/213+ 1/215+ 1/217+ 1/219+ 1/221+ 1/223+ 1/225+ 1/227+ 1/229+ 1/231+ 1/233+ 1/235+ 1/237+ 1/239+ 1/241+ 1/243+ 1/245+ 1/247+ 1/249+ 1/251+ 1/253+ 1/255+ 1/257+ 1/259+ 1/261+ 1/263+ 1/265+ 1/267+ 1/269+ 1/271+ 1/273+ 1/275+ 1/277+ 1/279+ 1/281+ 1/283+ 1/285+ 1/287+ 1/289+ 1/291+ 1/293+ 1/295+ 1/297+ 1/299+ 1/301+ 1/303+ 1/305+ 1/307+ 1/309+ 1/311+ 1/313+ 1/315+ 1/317+ 1/319+ 1/321+ 1/323+ 1/325+ 1/327+ 1/329+ 1/331+ 1/333+ 1/335+ 1/337+ 1/339+ 1/341+ 1/343+ 1/345+ 1/347+ 1/349+ 1/351+ 1/353+ 1/355+ 1/357+ 1/359+ 1/361+ 1/363+ 1/365+ 1/367+ 1/369+ 1/371+ 1/373+ 1/375+ 1/377+ 1/379+ 1/381+ 1/383+ 1/385+ 1/387+ 1/389+ 1/391+ 1/393+ 1/395+ 1/397+ 1/399+ 1/401+ 1/403+ 1/405+ 1/407+ 1/409 = 3.143260498314515 (ans) - 1/4 = 2.893260498314515 (ans) + 1/411+ 1/413+ 1/415+ 1/417+ 1/419+ 1/421+ 1/423+ 1/425+ 1/427+ 1/429+ 1/431+ 1/433+ 1/435+ 1/437+ 1/439+ 1/441+ 1/443+ 1/445+ 1/447+ 1/449+ 1/451+ 1/453+ 1/455+ 1/457+ 1/459+ 1/461+ 1/463+ 1/465+ 1/467+ 1/469+ 1/471+ 1/473+ 1/475+ 1/477+ 1/479+ 1/481+ 1/483+ 1/485+ 1/487+ 1/489+ 1/491+ 1/493+ 1/495+ 1/497+ 1/499+ 1/501+ 1/503+ 1/505+ 1/507+ 1/509+ 1/511+ 1/513+ 1/515+ 1/517+ 1/519+ 1/521+ 1/523+ 1/525+ 1/527+ 1/529+ 1/531+ 1/533+ 1/535+ 1/537+ 1/539+ 1/541+ 1/543+ 1/545+ 1/547+ 1/549+ 1/551+ 1/553+ 1/555+ 1/557+ 1/559+ 1/561+ 1/563+ 1/565+ 1/567+ 1/569+ 1/571+ 1/573+ 1/575+ 1/577+ 1/579+ 1/581+ 1/583+ 1/585+ 1/587+ 1/589+ 1/591+ 1/593+ 1/595+ 1/597+ 1/599+ 1/601+ 1/603+ 1/605+ 1/607+ 1/609+ 1/611+ 1/613+ 1/615+ 1/617+ 1/619+ 1/621+ 1/623+ 1/625+ 1/627+ 1/629+ 1/631+ 1/633+ 1/635+ 1/637+ 1/639+ 1/641+ 1/643+ 1/645+ 1/647+ 1/649+ 1/651+ 1/653+ 1/655+ 1/657+ 1/659+ 1/661+ 1/663+ 1/665+ 1/667+ 1/669+ 1/671+ 1/673 = 3.141796661628686
たとえ証明が抽象的に見えても、その手順を具体的に実行してみると、すんなり理解できることがあります。今回のケースはまさにそんな実例になっていましたね。
それでは今日はこの辺で!