モジュラー曲線(4)：レベル構造付き楕円曲線とモジュライ空間

前回の記事では、モジュラー曲線 $Y(1)$ と楕円曲線の同型類全体が全単射であることを示しました。すなわち、 $Y(1)$ は楕円曲線の（同型類の）モジュライ空間になっているということでした。
tsujimotter.hatenablog.com

今回はレベル構造が入ったモジュラー曲線 $Y_1(N)$ を考えたいと思います。このモジュラー曲線は一体何のモジュライ空間なのかというのが今回の主題です。

実は、上の話の類似で、 $Y_1(N)$ はレベル構造が付いた楕円曲線のモジュライ空間になっています。今日はそれを示すのを目的とします。

前提知識等

今回の記事はモジュラー曲線シリーズの記事の内容を前提としています。
tsujimotter.hatenablog.com

シリーズ記事をまだ読んでいない方は、一通り参照してから本記事を読まれることを推奨します。

特に、前回の記事「モジュラー曲線(3)：複素トーラスとしての楕円曲線」は関連度が高く、命題をいくつか引用します。

前提知識等

目次

0. モジュラー曲線

1. レベル構造付き楕円曲線

2. レベル構造付き楕円曲線の同型射

3. 上半平面とレベル構造付き楕円曲線

4. レベル構造付き楕円曲線のモジュライ空間

5. おわりに

補足１：同型なレベル構造付き楕円曲線の作り方

補足２：のモジュライ解釈

参考文献

次回の記事

0. モジュラー曲線 $Y_1(N)$

合同部分群について復習しましょう。

モジュラー群 $\Gamma := \operatorname{SL}_2(\mathbb{Z})$ には、正の整数 $N$ に対して合同部分群と呼ばれる部分群

$\Gamma(N) \subset \Gamma_1(N) \subset \Gamma_0(N) \subset \Gamma$

が存在しました。

今回は、合同部分群の中でも、特に $\Gamma_1(N)$ の定義を思い出しましょう。

$\Gamma_1(N) := \left\{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \Gamma \; \middle| \; c \equiv 0, \;\; d \equiv 1 \pmod{N} \right\}$

つまり

$\begin{pmatrix} a & b \\ c & d \end{pmatrix} \equiv \begin{pmatrix} * & * \\ 0 & 1 \end{pmatrix} \pmod{N}$

という形の行列全体を考えるということです。

「何でこんな条件なの？」と思うかもしれませんが、この理由は最後の方でわかります。

$\Gamma_1(N)$ も $\Gamma$ と同様に上半平面 $H$ に作用します。そこで、 $\Gamma_1(N)$ の作用で割った空間

$Y_1(N) := \Gamma_1(N)\backslash H$

を考えます。この $Y_1(N)$ を $\Gamma_1(N)$ に関するモジュラー曲線と言います。

また、上半平面に無限遠点と $\mathbb{Q}$ の元を加えてできる拡張された上半平面 $H^* = H \cup \mathbb{Q} \cup \{ \sqrt{-1} \infty \}$ を考えて、それを $\Gamma_1(N)$ の作用で割った空間を

$X_1(N) := \Gamma_1(N)\backslash H^*$

と表します。これも $\Gamma_1(N)$ に関するモジュラー曲線といいます。

$Y_1(N)$ と $X_1(N)$ の違いは、コンパクトかどうかです。 $X_1(N)\setminus Y_1(N)$ の元をカスプといいますが、カスプが付け加えられることで、 $X_1(N)$ はコンパクトな空間になります。

なお、モジュライ空間を考えるときにはカスプは不要なので、 $X_1(N)$ は今回は扱いません。

さて、 $Y_1(N)$ の連結な代表元を集めた図形を $\Gamma_1(N)$ の基本領域といいます。基本領域は、 $Y_1(N)$ の形を表していると言えますが、一体どんな図形になっているのでしょうか。

モジュラー群 $\Gamma$ の基本領域 $\Omega$ は次のようなものでした。

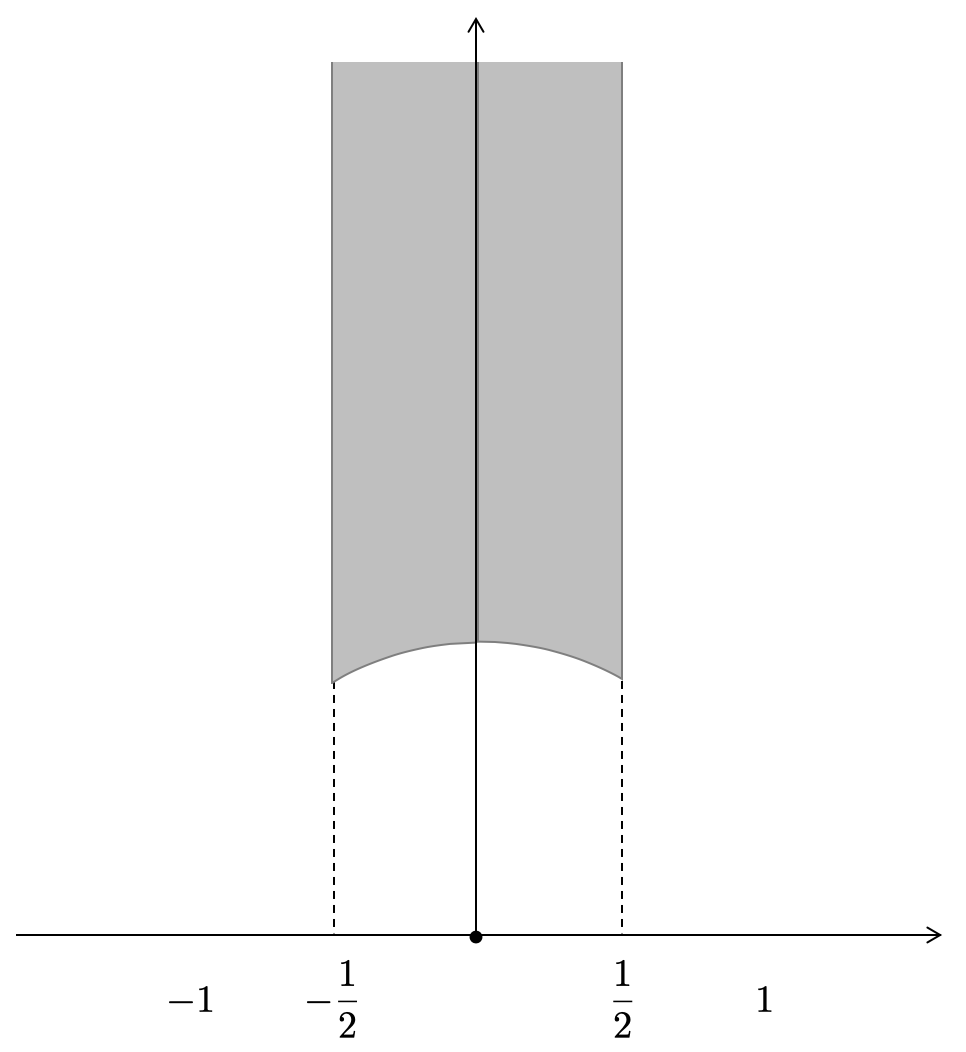
f:id:tsujimotter:20190709092846p:plain:w240

$\Gamma/\Gamma_1(N)$ の剰余類の代表元の集合 $\{ \gamma_1, \ldots, \gamma_n \}$ を考えます。これは

$\displaystyle \Gamma = \bigcup_{i=1}^{n} \Gamma_1(N) \gamma_i$

を満たします。代表元の選び方を工夫すれば $\Omega$ に $\{ \gamma_1, \ldots, \gamma_n \}$ を作用させてできる図形

$\displaystyle \Omega(\Gamma_1(N) ) = \bigcup_{i=1}^{n} \gamma_i(\Omega)$

を連結にとることができます。これが $\Gamma_1(N)$ の基本領域となります。

それでは、 $\Gamma_1(N)$ の基本領域 $\Omega(\Gamma_1(N) )$ を図示してみましょう。

しかしながら、実はこれが難しい。まず剰余類の個数は

$\displaystyle [\Gamma : \Gamma_1(N)] = N^2\prod_{p \mid N}\left(1 - \frac{1}{p^2}\right)$

となります。たとえば、 $N = 11$ のときは $120$ 個になります。多いのです。

しかも $120$ 個を選んだとして、それによって写された領域が連結になるとは限りません。したがって、連結になるように120個のパズルのピースを組み立てる必要があります。

$\Gamma_0(11)$ のときはネットを探して正解の図形を見つけたので、それを見ながら代表元を探すことができましたが、今回は正解も見つかりません。

そんなわけで、この問題は実は２年ぐらい前からずっと悩んでいまして、半ば諦めていたのですが・・・。

つい先日、方法を見つけました。

参考：
sagemath - Drawing fundamental domains with sage - Mathematics Stack Exchange

sagemathというソフトで、合同部分群に関する基本領域を描画する機能があるというのです。sagemathすごい！

仕様はこちらに書いてありました：
Farey Symbol for arithmetic subgroups of ${\rm PSL}_2(\ZZ)$ — Sage 9.5 Reference Manual: Arithmetic Subgroups of ${\rm SL}_2({\bf Z})$

それでは、以下のコマンドを実行してみましょう。

G = Gamma1(11); G
FareySymbol(G).fundamental_domain(ymax = 1.2)

なんと、一発で $\Gamma_1(11)$ の基本領域が描画されます。

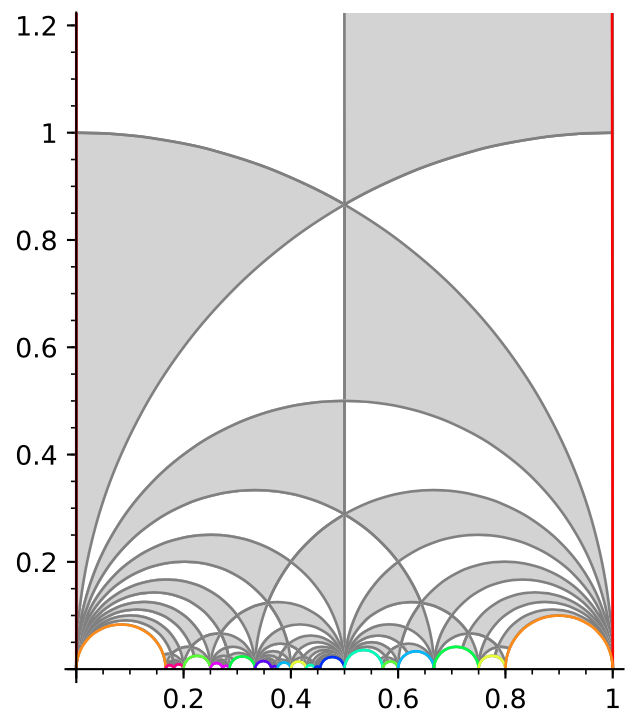
f:id:tsujimotter:20190708205606p:plain:w300

おお、こんな形をしていたのですね！！

少しだけ、図形の見方を説明します。 $\Gamma$ の基本領域として以下のような図形を紹介しましたが、実際はこのような基本領域の選び方には任意性があります。

f:id:tsujimotter:20190709010620p:plain:w240

上の図形を縦に半分に切って、片側を $\Gamma$ の変換によって次のように写した図形も $\Gamma$ の基本領域となります。

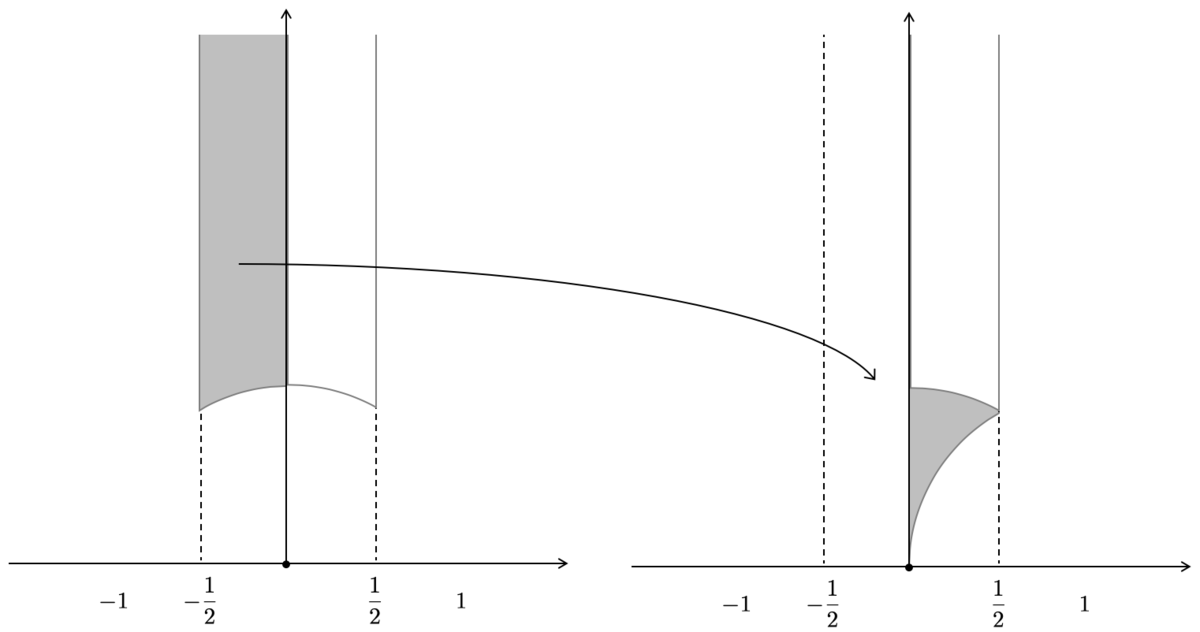
f:id:tsujimotter:20190709010753p:plain:w500

この図形を $\Omega'$ とし、 $\Omega'$ に対して適切な $\Gamma/\Gamma_1(N)$ の代表元を作用させてできた図形が、sagemathの計算した $\Gamma_1(11)$ の基本領域というわけです。

以上でモジュラー曲線 $Y_1(N)$ の導入は終わりですが、今回の主題は

$Y_1(N)$ は何に対するモジュライ空間なのか？

ということです。

$\Gamma$ に関する基本領域と $\Gamma_1(N)$ に関する基本領域を比べてみると、明らかに後者の方が大きくなっていました。

f:id:tsujimotter:20190709010217p:plain:w400

ちょうどコセットの個数 $[\Gamma : \Gamma_1(N)]$ 倍の大きさになっています。したがって、前回やったように、試しに楕円曲線の同型類をそのまま割り当ててしまうと、１つの楕円曲線の同型類に対して、複数の点（具体的には $[\Gamma : \Gamma_1(N)]$ 個の点）が重複して対応してしまいます。

ぴったり $Y_1(N)$ の点と対応させるためには、楕円曲線の同型類では、少々おおざっぱすぎることがわかります。そこで、同型の取り方をもう少し細かくしようという発想が出てきます。それが、レベル構造付き楕円曲線のアイデアです。

1. レベル構造付き楕円曲線

任意の $\mathbb{C}$ 上の楕円曲線 $E$ は、格子 $\Lambda \subset \mathbb{C}$ が存在して $E \simeq \mathbb{C}/\Lambda$ と表せるので、今回も楕円曲線といったら $\mathbb{C}/\Lambda$ を指すものとしましょう。

また、前回に引き続き以下の記法を用います。

格子の基底が $\{\omega_1, \omega_2\}$ であることを明示するときは、 $\Lambda_{\omega_1, \omega_2}$ と表現。
格子の基底が $\{ \tau, 1 \}$ であることを明示するときは、 $\Lambda_{\tau}$ と表現。

楕円曲線 $\mathbb{C}/\Lambda$ には正の整数 $N$ に対して自分自身への同種写像である「 $N$ 倍写像」があります。 $\mathbb{C}/\Lambda$ の点 $P$ に対して

$NP = 0$

を満たす最小の $N$ を $P$ の位数といいます。ここで位数がちょうど $N$ である点を考えます。

たとえば、 $N = 5$ のときは、次の点が位数 $N$ の点です。

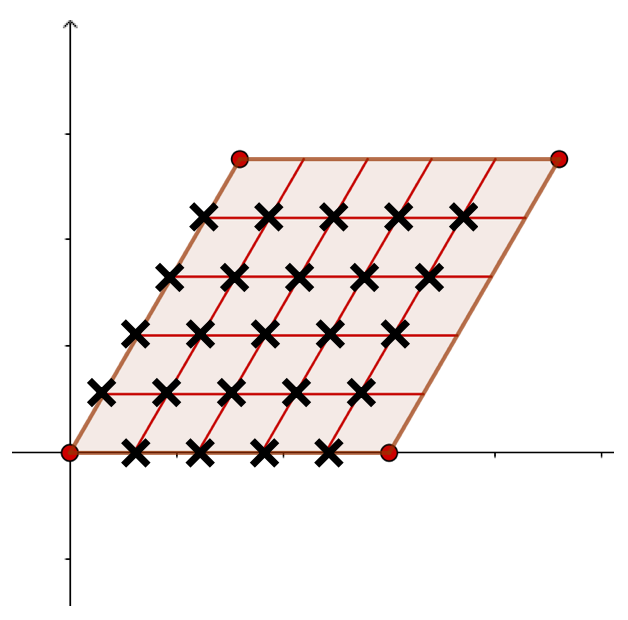
f:id:tsujimotter:20190709003240p:plain:w240

たとえば、 $N = 6$ のときは、次の点が位数 $N$ の点です。

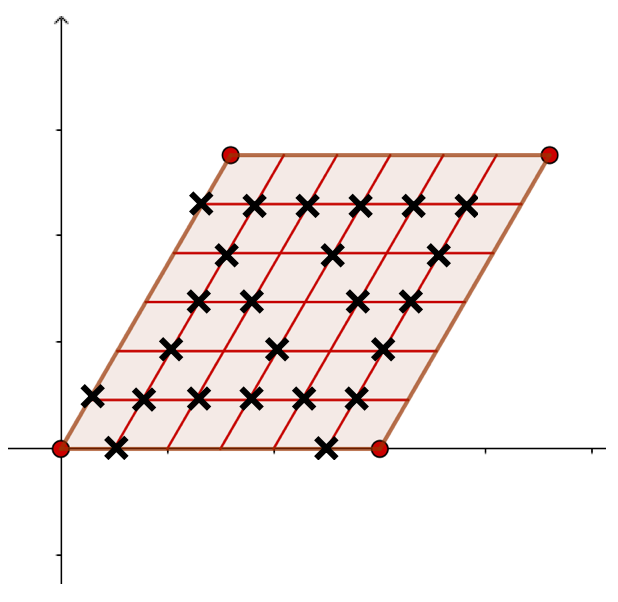
f:id:tsujimotter:20190709003305p:plain:w240

楕円曲線を $\mathbb{C}/\Lambda$ とし、その位数 $N$ の点のうち１点を選んで $P$ とします。この $\mathbb{C}/\Lambda$ と $P$ の組

$(\mathbb{C}/\Lambda, P)$

を レベル構造付き楕円曲線 と呼びます。

$(\mathbb{C}/\Lambda, P)$ のような書き方に慣れていない人は、なんだこれはと思うかもしれませんので、一言補足します。

$\mathbb{C}/\Lambda$ のような台となる集合や群に、 $P$ のような構造を加えたものを考えることがあります。これを付加構造といいます。

たとえば、位相空間を思い浮かべると、良い例になっていると思います。位相空間 $(X, \mathcal{O})$ は台となる集合 $X$ があり、それに開集合系 $\mathcal{O}$ という付加構造を考えますね。

この手の例は、ほかにもいくつかあげることができます。

アフィンスキーム $(X, \mathcal{O}_X)$ ：環のスペクトル $X = \operatorname{Spec}(A)$ に層 $\mathcal{O}_X$ を付加構造として加えたもの
基点付き位相空間 $(X, x_0)$ ：位相空間 $X$ に基点 $x_0$ を付加構造として加えたもの

大事なことは、付加構造込みで一つの対象だと思うという点です。楕円曲線に付加構造として位数 $N$ の点を入れたものは、たとえ楕円曲線として同型であっても、付加構造の点が異なれば別のものとみなされるというわけです。

2. レベル構造付き楕円曲線の同型射

次に、レベル構造付き楕円曲線における同型射を定義しましょう。

以下、レベルを $N$ に固定します。２つのレベル構造付き楕円曲線 $(\mathbb{C}/\Lambda, P), \; (\mathbb{C}/\Lambda', P')$ を考えます。

ここで楕円曲線の間の同型射

$\phi \colon \mathbb{C}/\Lambda \xrightarrow{\;\sim\;} \mathbb{C}/\Lambda'$

があるとします。これは単なる楕円曲線としての同型射です（定義は前回の記事参照）。

写像 $\phi$ によって $P$ が $P'$ に写されるとき、すなわち

$\phi(P) = P'$

が成り立つとき、 $\phi$ はレベル構造付き楕円曲線としての（ $\mathbb{C}$ 上の）同型射であるといいます。

$(\mathbb{C}/\Lambda, P)$ と $(\mathbb{C}/\Lambda', P')$ の間に同型射が存在するとき、 $(\mathbb{C}/\Lambda, P)$ と $(\mathbb{C}/\Lambda', P')$ はレベル構造付き楕円曲線として（ $\mathbb{C}$ 上）同型であるといい

$(\mathbb{C}/\Lambda, P) \simeq (\mathbb{C}/\Lambda', P')$

と表します。

単なる楕円曲線のときより、同型射の条件が厳しくなっていることがわかるでしょうか。

楕円曲線として同型射であったとしても、 $\phi(P) = P'$ でなければ、レベル構造付き楕円曲線としては同型でないということです。

たとえば、２つのレベル付き楕円曲線 $(\mathbb{C}/\Lambda, \; P), \; (\mathbb{C}/\Lambda', \; P')$ を図のようにとりましょう。

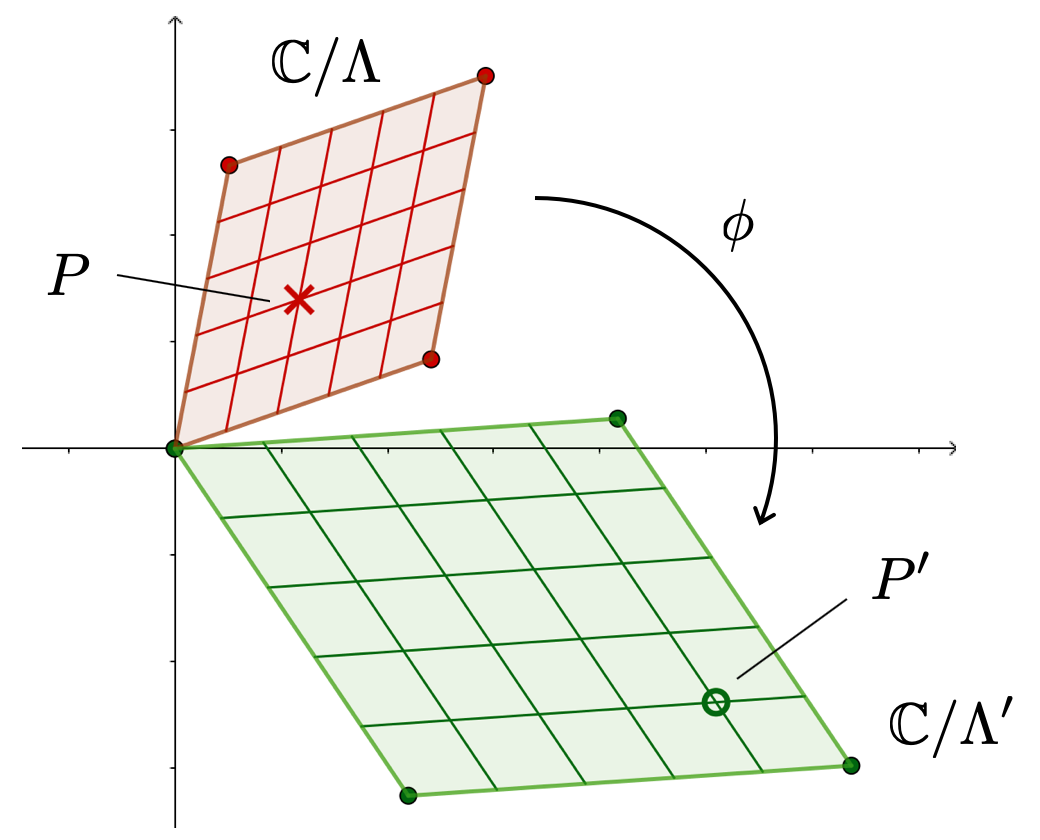
f:id:tsujimotter:20190708225426p:plain:w280

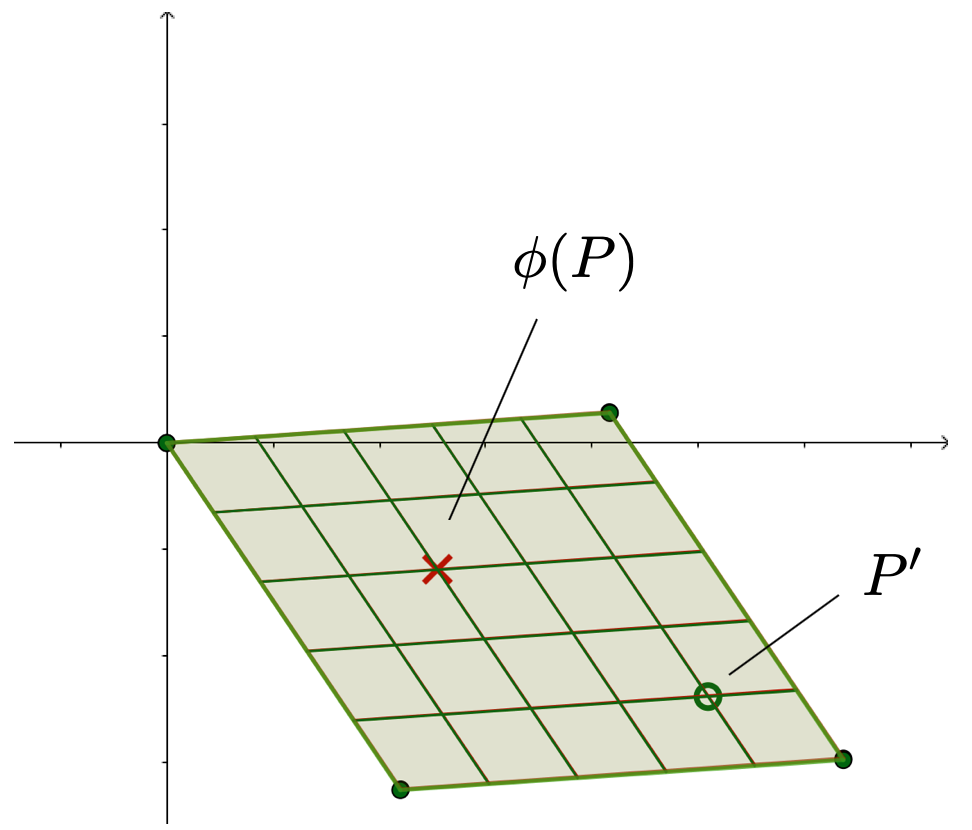
これらは同型写像 $\phi$ を通して、楕円曲線としては同型となります（格子点がぴったり一致するように写せます）。しかしながら、 $\phi(P) \neq P'$ となり、レベル構造付き楕円曲線としては同型ではありません。

f:id:tsujimotter:20190708225454p:plain:w280

同型が定義できたので、レベル構造付き楕円曲線 $(\mathbb{C}/\Lambda, \; P)$ の同型類を次のように定義します。

$[(\mathbb{C}/\Lambda, \; P)] := \{ (\mathbb{C}/\Lambda', \; P') \mid (\mathbb{C}/\Lambda', \; P')\simeq (\mathbb{C}/\Lambda, \; P) \}$

このレベル構造付き楕円曲線の同型類全体を集めたものを $S_1(N)$ とします。

$S_1(N) := \{ \text{レベル構造付き楕円曲線}\,(\mathbb{C}/\Lambda, \; P) \, \text{全体}\}/\simeq$

$S_1(N)$ を定義したことにより、0章で述べた「同型の取り方をもう少し細かくしよう」という話が説明できます。

上で図示して説明した例は、楕円曲線としては同型であるので「楕円曲線としては」同じ同型類に属します。一方で、 $\phi(P) \neq P'$ であるので「レベル構造付き楕円曲線としては」同型ではないのです。

付加構造を考えることで、楕円曲線全体の空間を「より細かく分類する方法」を我々は手に入れました。レベル構造付き楕円曲線の同型類全体 $S_1(N)$ を考えると、単なる楕円曲線の同型類全体 $\mathcal{ELL}_{\mathbb{C}}$ よりは同型類の個数が多くなります。

以降では、こうして得られたより細かな分類 $S_1(N)$ が、ちょうどぴったり $Y_1(N)$ と全単射を持つという話をしたいと思います。

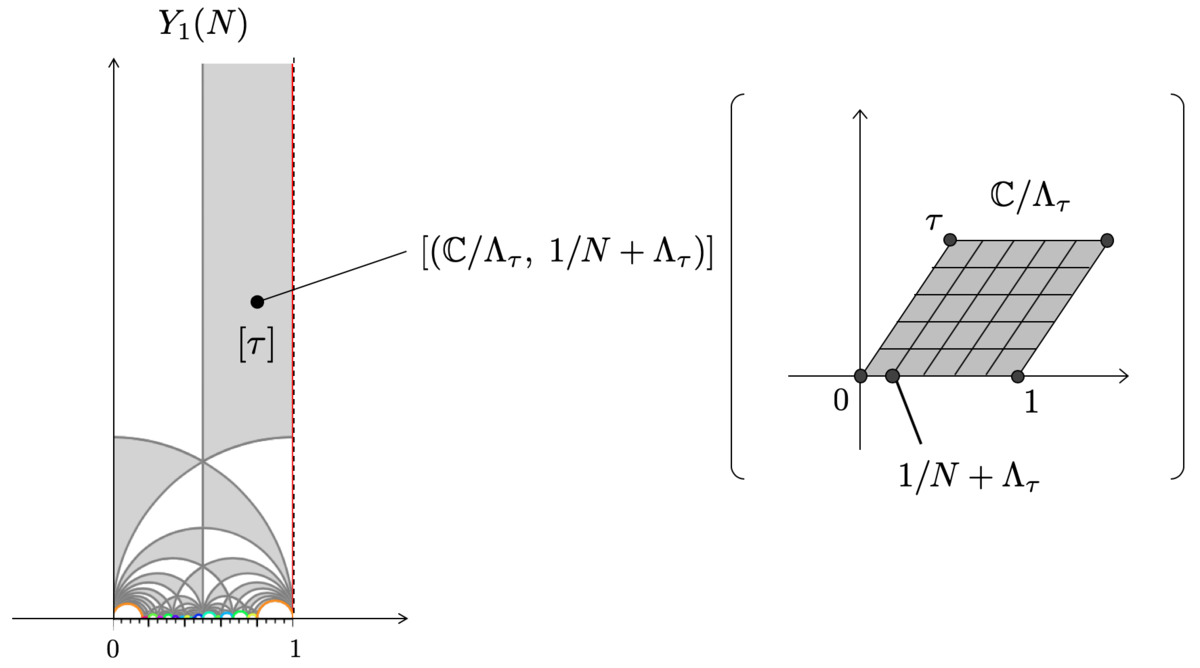
3. 上半平面とレベル構造付き楕円曲線

ここでは、上半平面 $H$ 上の点に対してレベル構造付き楕円曲線を対応させる方法について述べたいと思います。

前回、 $\tau \in H$ に対して、楕円曲線 $\mathbb{C}/\Lambda_{\tau}$ を対応させるルールを与えました。これをそのまま使います。

あとは、 $\mathbb{C}/\Lambda_{\tau}$ の位数 $N$ の点のうち、どれを対応させるかを決める必要があります。ここでは、 $1/N + \Lambda_{\tau}$ を選びます（下図）。

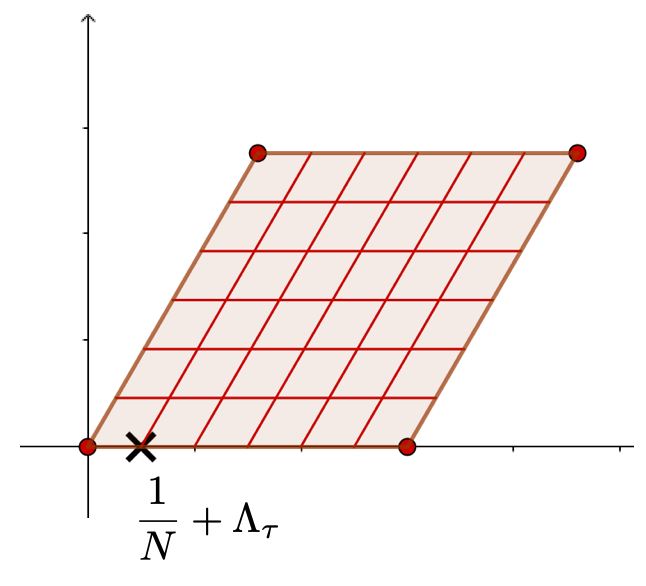
f:id:tsujimotter:20190708235813p:plain:w260

このようにして選んだ $(\mathbb{C}/\Lambda_\tau, \; 1/N + \Lambda_{\tau})$ こそが、上半平面 $H$ の点 $\tau$ に対応するレベル構造付き楕円曲線です。

実はこの対応関係について私はものすごく「もやっと」していたのです。

今回対応させた点は、 $1/N + \Lambda_{\tau}$ という形のものだけです。つまり、位数 $N$ の点の中で、特に「左下の隅にある特定の点」しか選んでいないわけです。

一方で、レベル構造付き楕円曲線全体を考えると、楕円曲線とその位数 $N$ の点のすべての組み合わせを考えているはずです。

これじゃあ全然足りないじゃないか。実は、 $\tau \in H$ に対応しないレベル構造付き楕円曲線とかあるんじゃないか？

そんなことを考えながら、しばらく悶々としていました。ところが、実はそうではないということがわかりました。それを主張するのが次の命題です。

命題1

任意のレベル構造付き楕円曲線 $(E, \; P)$ に対して、 $\tau \in H$ が存在して

$(E, \; P) \simeq (\mathbb{C}/\Lambda_{\tau}, \; 1/N + \Lambda_\tau)$

が成り立つ．すなわち

$S_1(N) = \{ [(\mathbb{C}/\Lambda_{\tau}, \; 1/N + \Lambda_\tau)] \mid \tau \in H \}$

が成り立つ．

これは、前回の「複素トーラスとしての楕円曲線」の記事の命題4に対応する命題です。

つまり、任意のレベル構造付き楕円曲線をとってきたとして、それに対応する $\tau \in H$ の点があるといっているわけですね。つまり

$[(\mathbb{C}/\Lambda_{\tau}, \; 1/N + \Lambda_{\tau})]$

という形のものだけを考えれば、同型類としては十分であった、というわけです。これは私にとってはとても意外なことで、正直驚きました。

証明は結構込み入っているのですが、ポイントとなるのは次の２点だと思います。

一つは、楕円曲線 $\mathbb{C}/\Lambda_{\tau'}$ における「任意の位数 $N$ の点 $Q$ 」は、 $\gcd(c, d, N) = 1$ なる整数 $c, d$ を用いて

$\displaystyle Q = \frac{c\tau' + d}{N} + \Lambda_{\tau'}$

とかけるということです。

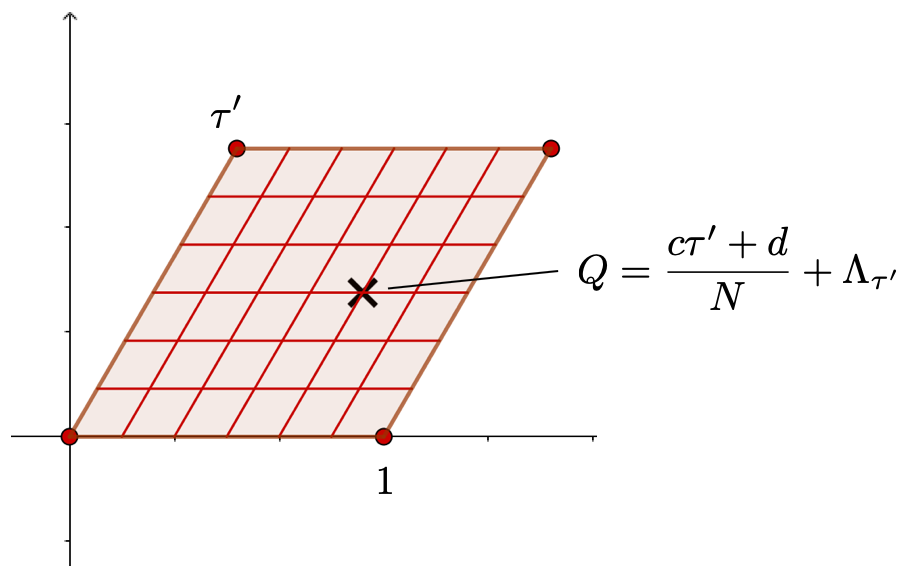
f:id:tsujimotter:20190710133432p:plain:w320

$c, d$ の条件は、 $Q$ の位数が「ちょうど $N$ 」であることから従います。もし、 $\gcd(c, d, N) = M$ なる $M > 1$ が存在すれば

$\displaystyle \frac{N}{M}\cdot \frac{c\tau' + d}{N} + \Lambda_{\tau'} = 0 + \Lambda_{\tau'}$

となってしまいます。つまり、 $Q$ は位数 $N/M$ の点であったということです（それはおかしい）。 $c, d$ の条件はこの対偶です。

二つめのポイントは、全射

$\operatorname{SL}_2(\mathbb{Z}) \twoheadrightarrow \operatorname{SL}_2(\mathbb{Z}/N\mathbb{Z})$

の存在です。行列の各成分について $\bmod{N}$ をとる写像は全射になるということです。これは明らかですね。

全射性より、 $\operatorname{SL}_2(\mathbb{Z}/N\mathbb{Z})$ の元 $\overline{\gamma}$ があると、 $\bmod{N}$ して $\overline{\gamma}$ になる $\operatorname{SL}_2(\mathbb{Z})$ の行列 $\gamma'$ が存在することが言えます。

また、前回最後に示した「補題6」も使うことになりますので、再掲しておきましょう。

前回の補題6（再掲）

$\omega_1, \omega_2, \omega_1', \omega_2' \in \mathbb{C}$ を $\operatorname{Im}(\omega_1/\omega_2) > 0, \; \operatorname{Im}(\omega_1'/\omega_2') > 0$ となるようにとるとき，以下の (i), (ii) は同値である．

(i) $\Lambda_{\omega_1, \omega_2} = \Lambda_{\omega_1', \omega_2'}$
(ii) $\gamma \in \operatorname{SL}_2(\mathbb{Z})$ が存在して，次が成り立つ：

$\displaystyle \begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix} = \gamma \begin{pmatrix} \omega_1' \\ \omega_2' \end{pmatrix}$

それでは、ポイントを押さえたところで命題1の証明に行きたいと思います。少々長いのですが、頑張ってついてきてください。

（命題1の証明）

任意のレベル構造付き楕円曲線の同型類 $[(E, \; P)] \in S_1(N)$ をとります。

このとき、「前回の命題4」より $E$ はある $\tau' \in H$ が存在して、楕円曲線としての同型写像

$\phi_1 \colon E \xrightarrow{\;\; \sim \;\;} \mathbb{C}/\Lambda_{\tau'}$

があります。また、 $\phi_1$ によって $\phi_1(P) = Q$ と対応する点 $Q \in \mathbb{C}/\Lambda_{\tau'}$ を、 $c, d \in \mathbb{Z}$ として次のように表すことができます。

$\displaystyle Q = \frac{c\tau' + d}{N} + \Lambda_{\tau'}$

これによってレベル構造付き楕円曲線の同型射

$\phi_1\colon (E, \; P) \xrightarrow{\;\;\sim\;\;} (\mathbb{C}/\Lambda_{\tau'}, \;Q) \tag{A}$

が一つ得られました。

また、このとき点 $Q$ の位数はちょうど $N$ なので、 $\gcd(c, d, N) = 1$ が言えます。よって、ユークリッドの互除法により

$ad - bc - kN = 1$

なる $a, b, k \in \mathbb{Z}$ が存在します。

上で得られた $a, b, c, d$ を用いて行列

$\gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in M_2(\mathbb{Z})$

を考えます。（ $\gamma$ は $\operatorname{SL}_2(\mathbb{Z})$ の元とは限らないことに注意！）

$ad - bc = 1 + kN \equiv 1 \pmod{N}$ より、上記の行列 $\gamma$ の各成分を $\bmod{N}$ して得られる行列 $\overline{\gamma}$ は、 $\operatorname{SL}_2(\mathbb{Z}/N\mathbb{Z})$ の行列になります。

ここで、 $\gamma$ を $\bmod{N}$ することは $Q = (c\tau' + d)/N + \Lambda_{\tau'}$ に対して影響を与えないことに注意します。

また、上で議論したように、 $\operatorname{SL}_2(\mathbb{Z})$ に対して $\bmod{N}$ をとる写像は全射です。したがって、この全射で $\overline{\gamma} \in \operatorname{SL}_2(\mathbb{Z}/N\mathbb{Z})$ に対応する $\operatorname{SL}_2(\mathbb{Z})$ の元 $\gamma' = \begin{pmatrix} a' & b' \\ c' & d' \end{pmatrix}$ がとれます。

$\begin{matrix} \operatorname{SL}_2(\mathbb{Z}) & \overset{\;\bmod{N}\;}{\longrightarrow} & \operatorname{SL}_2(\mathbb{Z}/N\mathbb{Z}) \\ \gamma' & \longmapsto & \overline{\gamma} \end{matrix}$

以上の議論により我々は

$\displaystyle \gamma' = \begin{pmatrix} a' & b' \\ c' & d' \end{pmatrix} \in \operatorname{SL}_2(\mathbb{Z})$

であって

$\displaystyle Q = \frac{c'\tau' + d'}{N} + \Lambda_{\tau'}$

を満たす行列を手に入れました。

ここで $\tau = \gamma' \tau'$ とし、 $\alpha = c'\tau' + d'$ とします。このとき

$\displaystyle \alpha \tau = (c'\tau' + d')\frac{a'\tau' + b'}{c'\tau' + d'} = a'\tau' + b'$

となります。すると

$\begin{pmatrix} \alpha \tau \\ \alpha \end{pmatrix} = \begin{pmatrix} a' & b' \\ c' & d' \end{pmatrix} \begin{pmatrix} \tau' \\ 1 \end{pmatrix}$

となりますが、「前回の補題6の(ii) $\Longrightarrow$ (i)」を用いると

$\Lambda_{\alpha\tau, \alpha} = \Lambda_{\tau', 1}$

となります。よって

$\alpha \Lambda_{\tau} = \Lambda_{\tau'}$

です。したがって、楕円曲線としての同型写像

$\phi_2\colon \mathbb{C}/\Lambda_{\tau} \xrightarrow{\;\;\sim \;\;} \mathbb{C}/\Lambda_{\tau'}$

が得られます。

また、写像 $\phi_2$ によって

$\displaystyle \phi_2\left(\frac{1}{N} + \Lambda_{\tau}\right) = \frac{\alpha}{N} + \Lambda_{\tau'} = \frac{c'\tau' + d'}{N} + \Lambda_{\tau'} = Q$

を満たします。

すなわち、レベル構造付き楕円曲線としての同型射

$\phi_2\colon (\mathbb{C}/\Lambda_{\tau}, \; 1/N + \Lambda_{\tau}) \xrightarrow{\;\;\sim \;\;} (\mathbb{C}/\Lambda_{\tau'}, \; Q) \tag{B}$

が得られました。

$(A), (B)$ で得られた２つの同型射 $\phi_1, \phi_2$ の合成

$(E, \; P) \; \xrightarrow{\phi_1 }\; (\mathbb{C}/\Lambda_{\tau'}, \; Q) \; \xrightarrow{\phi_2^{-1} } \; (\mathbb{C}/\Lambda_{\tau}, \; 1/N + \Lambda_{\tau})$

により、任意のレベル構造付き楕円曲線 $(E, \; P)$ に対して、 $\tau \in H$ が存在して $(E, \; P)$ に同型な $(\mathbb{C}/\Lambda_{\tau}, \; 1/N + \Lambda_{\tau})$ が得られました。

証明の手順を辿れば、任意の $(\mathbb{C}/\Lambda, \; P)$ と同型な $(\mathbb{C}/\Lambda_{\tau}, \; 1/N + \Lambda_{\tau})$ を具体的に計算することもできるでしょう。

せっかくなので「補足１：同型なレベル構造付き楕円曲線の作り方」で計算してみたいと思います。

4. レベル構造付き楕円曲線のモジュライ空間

最後に、 $Y_1(N)$ と $S_1(N)$ の間にちょうどぴったり全単射があることを示しましょう。

そのために、以下の命題を証明します。

命題2

$\tau, \; \tau' \in H$ としたとき，以下の (i), (ii) は同値である．

(i) $(\mathbb{C}/\Lambda_{\tau}, \; 1/N + \Lambda_{\tau}) \simeq (\mathbb{C}/\Lambda_{\tau'}, \; 1/N + \Lambda_{\tau'})$
(ii) $\gamma \in \Gamma_1(N)$ が存在して $\tau = \gamma \tau'$

この命題は「複素トーラスとしての楕円曲線」の記事の命題5に対応しています。以下のように置き換えたものになっています。

前回命題5「楕円曲線の同型」を「レベル構造付き楕円曲線の同型」に
前回命題5「 $\operatorname{SL}_2(\mathbb{Z})$ 」を「 $\Gamma_1(N)$ 」に

それでは証明に入りましょう。

（命題2の証明）

(i) $\Longrightarrow$ (ii) を示す：
$\tau, \tau' \in H$ に対して

$(\mathbb{C}/\Lambda_{\tau}, \; 1/N + \Lambda_{\tau}) \simeq (\mathbb{C}/\Lambda_{\tau'}, \; 1/N + \Lambda_{\tau'})$

が成り立つと仮定します。

このとき、楕円曲線としての同型 $\mathbb{C}/\Lambda_{\tau} \simeq \mathbb{C}/\Lambda_{\tau'}$ より、ある $\alpha \in \mathbb{C}^\times$ が存在して

$\alpha \Lambda_{\tau} = \Lambda_{\tau'} \tag{1}$

が成り立ちます（「前回の命題3」より）。また、レベル構造付き楕円曲線の同型射の条件より

$\displaystyle \alpha\left( \frac{1}{N} + \Lambda_{\tau} \right) = \frac{1}{N} + \Lambda_{\tau'} \tag{2}$

も成り立ちます。

$(1)$ と「前回の補題6」の(i) $\Longrightarrow$ (ii)より

$\begin{pmatrix} \alpha \tau \\ \alpha \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} \tau' \\ 1 \end{pmatrix}$

であるから、特に $\alpha = c\tau' + d$ が言えます。したがって、 $(2)$ より

$\displaystyle \frac{c\tau' + d}{N} + \Lambda_{\tau} = \frac{1}{N} + \Lambda_{\tau'}$

が言えるので、 $c\equiv 0, \; d \equiv 1 \pmod{N}$ がわかります。よって、 $\begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \Gamma_1(N)$ であることがわかります。

$\alpha \tau = a\tau' + b$ かつ $\alpha = c\tau' + d$ より

$\displaystyle \tau = \frac{\alpha \tau}{\alpha} = \frac{a\tau' + b}{c\tau' + d} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\tau'$

であり、 $\gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ として、 $\tau = \gamma \tau'$ を満たす $\gamma \in \Gamma_1(N)$ が存在することが言えました。

(ii) $\Longrightarrow$ (i) を示す：
$\gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \Gamma_1(N)$ が存在して $\tau, \tau' \in H$ が $\tau = \gamma \tau'$ を満たすと仮定します。

また、 $\alpha = c\tau' + d$ とします。このとき $\alpha\tau = (c\tau' + d)\frac{a\tau' + b}{c\tau' + d} = a\tau' + b$ より

$\begin{pmatrix} \alpha \tau \\ \alpha \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} \tau' \\ 1 \end{pmatrix}$

が言えます。このことから「前回の補題6」の(ii) $\Longrightarrow$ (i)より

$\Lambda_{\alpha\tau, \alpha} = \Lambda_{\tau', 1}$

であり、つまり

$\alpha\Lambda_{\tau} = \Lambda_{\tau'} \tag{3}$

が言えます。

また、 $1/N + \Lambda_{\tau}$ を $\alpha$ 倍することによって

$\displaystyle \alpha\left(\frac{1}{N} + \Lambda_{\tau} \right) = \frac{c\tau' + d}{N} + \Lambda_{\tau'} \tag{4}$

も言えます。

しかしここで、 $\Gamma_1(N)$ の定義より $c \equiv 0, \; d \equiv 1 \pmod{N}$ なので、 $(4)$ は

$\displaystyle \alpha\left(\frac{1}{N} + \Lambda_{\tau} \right) = \frac{1}{N} + \Lambda_{\tau'} \tag{4'}$

となります。

$(3), (4)'$ より、同型射

$(\mathbb{C}/\Lambda_{\tau}, \; 1/N + \Lambda_{\tau}) \xrightarrow{\;\; \sim \;\; } (\mathbb{C}/\Lambda_{\tau'}, \; 1/N + \Lambda_{\tau'})$

が存在することが言えました。

$\gamma = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ が $\alpha = c\tau' + d$ に化けることで、同型射として $\alpha$ 倍写像が具体的に構成できるということでした。

これを通して $\Gamma_1(N)$ の元に課された $c \equiv 0, \; d \equiv 1 \pmod{N}$ という謎の条件は

$\displaystyle \frac{c\tau' + d}{N} + \Lambda_{\tau'}= \frac{1}{N} + \Lambda_{\tau'}$

となるための必要十分条件だったことがわかります！

これで、 $\gamma \in \Gamma_1(N)$ が、レベル付き楕円曲線の同型写像と対応する理由がはっきりしました。うまいことできていますね！

ここまでくればあとは簡単です。命題2を使って目的の命題を示すことができます。

命題3

$S_1(N)$ をレベル構造付き楕円曲線の同型類全体の集合としたとき，次の写像は全単射である：

$\begin{matrix} Y_1(N) & \longleftrightarrow & S_1(N) \\ [\tau ]& \longmapsto & [(\mathbb{C}/\Lambda_{\tau}, \; 1/N+\Lambda_{\tau})] \end{matrix}$

この命題は「前回の命題7」に対応するものです。今回示した命題2と命題3があれば、簡単に示すことができます。

（命題3の証明）
$Y_1(N) \longrightarrow S_1(N)$ の well-defined 性を示す：
$[\tau] = [\tau'] \; \Longrightarrow \; [(\mathbb{C}/\Lambda_{\tau}, \; 1/N+\Lambda_{\tau})] = [(\mathbb{C}/\Lambda_{\tau'}, \; 1/N+\Lambda_{\tau'}) ]$ が
言えればよいが、これは命題3の (ii) $\Longrightarrow$ (i) より言える。

$Y_1(N) \longrightarrow S_1(N)$ の単射性を示す：
$[(\mathbb{C}/\Lambda_{\tau}, \; 1/N+\Lambda_{\tau})] = [(\mathbb{C}/\Lambda_{\tau'}, \; 1/N+\Lambda_{\tau'})] \; \Longrightarrow \; [\tau] = [\tau']$ が
言えればよいが、これは命題3の (i) $\Longrightarrow$ (ii) より言える。

$Y_1(N) \longrightarrow S_1(N)$ の全射性を示す：
任意のレベル構造付き楕円曲線の同型類 $[(\mathbb{C}/\Lambda, \; P) ] \in S_1(N)$ に対して、 $[(\mathbb{C}/\Lambda, \; P) ] = [(\mathbb{C}/\Lambda_{\tau}, \; 1/N+\Lambda_{\tau}) ]$ なる $\tau \in H$ が存在することが言えればよいが、これは命題2より言える。

5. おわりに

今回は、レベル構造付き楕円曲線について解説しました。楕円曲線に、 $N$ 等分点という構造を加えて同型写像を考えることで、単なる楕円曲線としての同型類より細かい分類を作ることができるのでした。

このアイデアにより、モジュラー曲線 $Y_1(N)$ とレベル構造付き楕円曲線の同型類 $S_1(N)$ の間に全単射が得られました。

f:id:tsujimotter:20190714141505p:plain:w420

モジュラー曲線 $Y_1(N)$ は、レベル構造付き楕円曲線のモジュライ空間だったということですね。

モジュラー曲線シリーズの記事は、当初は第３回で終わりの予定でしたが、もう少し書きたいことが残っています。今のところの予定では、あと２、３回程度は続くはずなので、よろしければ引き続きご覧になってください。

それでは、今日はこの辺で。

補足１：同型なレベル構造付き楕円曲線の作り方

簡単ですが、ノートでまとめてみたものを写真に撮りました。

f:id:tsujimotter:20190710144151j:plain:w400

時間があるときに、まとめ直したいと思います、

補足２： $Y_0(N)$ のモジュライ解釈

今回示したように、モジュラー曲線 $Y_1(N)$ は $N$ 等分点 $P$ を加えたレベル構造付き楕円曲線 $(E, P)$ のモジュライ空間となるのでした。

ところで、モジュラー曲線 $Y_0(N)$ に対しては、モジュライ空間として解釈できるのでしょうか。

実は、先ほどとは異なるタイプのレベル構造付き楕円曲線に対するモジュライ空間になることが示せます。楕円曲線の位数 $N$ の点 $P$ をとります。これは位数 $N$ なので、 $P$ が生成する巡回群 $C = \langle P \rangle$ が存在します。この $C$ を構造として加えた、レベル構造付き楕円曲線 $(E, \;C)$ を考えます。このようなレベル構造付き楕円曲線の同型射も同様に考えることができ、同型類全体を $S_0(N)$ とすると、全単射

$\begin{matrix} Y_0(N) & \longleftrightarrow & S_0(N) \\ [\tau] & \longmapsto & [(\mathbb{C}/\Lambda_{\tau}, \; \langle 1/N + \Lambda_\tau \rangle)] \end{matrix}$