ヴェイユ予想で遊んでみよう（その１）：楕円曲線の具体的計算

本記事は日曜数学 Advent Calendar 2025の1日目の記事です。

ご無沙汰しています。日曜数学者のtsujimotterです。

2025年も日曜数学アドベントカレンダーを立ち上げまして、今日の記事はその1日目の記事となります。今年もどんな記事が集まるのか、今から楽しみですね！

0. 今日やりたいこと

前回の記事では、数論の世界の大定理である「ヴェイユ予想」について、その主張を紹介しました。
tsujimotter.hatenablog.com

せっかくここまで丁寧に解説したので、今回はこのヴェイユ予想を具体例を通して計算してみたいと思います。

個人的には、こうした具体例の計算をする「遊び」が大好きです。
こうした遊びを通して、定理の主張や意義がより深く理解できたりするのも面白いなと思っています。

今回の記事は、前回の内容を前提とする記事となっています。
アドベントカレンダー的には、一話完結ではない「続きもの」の記事はちょっと不向きかな・・・とも思ったのですが、ご容赦いただけますと幸いです。

有限体 $\mathbb{F}_p$ 上の代数曲線を $C$ としたとき、有限体の列

$\mathbb{F}_{p}, \; \mathbb{F}_{p^2}, \; \mathbb{F}_{p^3}, \; \mathbb{F}_{p^4}, \; \mathbb{F}_{p^5}, \; \ldots$

を考えます。これらに対応する曲線 $C$ の有理点の個数

$\# C(\mathbb{F}_{p}), \; \# C(\mathbb{F}_{p^2}), \; \# C(\mathbb{F}_{p^3}), \; \# C(\mathbb{F}_{p^4}), \; \# C(\mathbb{F}_{p^5}), \; \ldots$

をすべて求めたいというのが、今回やりたいことです。

有限体の点だけを考えているので、有限通りの $(x, y)$ 座標を考えれば、一つひとつの有理点の個数は計算できます。しかしながら、それではすべての $n$ について $\# C(\mathbb{F}_{p^n})$ を考えたことにはなりません。

実は、ヴェイユ予想の４つの定理を駆使すると、最初のいくつか（１個とか２個とか）を計算するだけで、その先のすべての $\# C(\mathbb{F}_{p^n})$ を決定できるのです。

一を聞いて十を知る
ならぬ
一を聞いて $\infty$ を知る
です。

そんな不思議なことが起きるんですね。

今回は、2つの例を具体的に計算してみたいと思います：

（前編・本日の記事） $\mathbb{F}_{5}$ 上の楕円曲線（種数1）
（後編・次回の記事）超楕円曲線（種数2）

12/1に間に合わなかったので、下の例については次回の記事で計算したいと思います。

1. 楕円曲線の $\mathbb{F}_{5^n}$ 有理点の個数

それではまずは楕円曲線の例から行きましょう。

$q = 5$ として、 $\mathbb{F}_{5}$ 上の楕円曲線

$E\colon y^2 = x^3 + x + 1 \tag{1}$

について考えていきます。

係数が $\mathbb{F}_5$ なので、 $\mathbb{F}_{5^n}$ 有理点の個数 $\# E(\mathbb{F}_{5^n})$ について考えてみたいと思います。

まず、 $n = 1$ のときは、 $\mathbb{F}_5$ 上の有理点の個数を考えれば良いわけです。要するに、 $\bmod{5}$ で

$y^2 \equiv x^3 + x + 1\pmod{5}$

を満たす $(x, y)$ の組を数え上げればよいことになります。

ここで、右辺の $x$ に $x \in \mathbb{F}_5 = \{0, 1, 2, 3, 4\}$ を代入していき、（これが $y^2$ に等しいことから）この値が平方剰余であるかどうかを確認すればよいことになります。

$x$	$x^3 + x + 1$	対応する $y$
$0$	$0^3 + 0 + 1 = 1$	$1, \; 4$
$1$	$1^3 + 1 + 1 = 3$	$-$
$2$	$2^3 + 2 + 1 = 1$	$1, \; 4$
$3$	$3^3 + 3 + 1 = 1$	$1, \; 4$
$4$	$4^3 + 4 + 1 = 4$	$2, \; 3$

よって、これらに無限遠点 $\mathcal{O}$ を加えて

$E(\mathbb{F}_5) = \{ (0, 1), (0, 4), (2, 1), (2, 4), (3, 1), (3, 4), (4, 2), (4, 3), \mathcal{O} \}$

がすべての $\mathbb{F}_5$ -有理点となります。よって、その個数は

$\# E(\mathbb{F}_5) = 9$

です。

無限遠点を除く点をグラフで表すと、次のようになります：

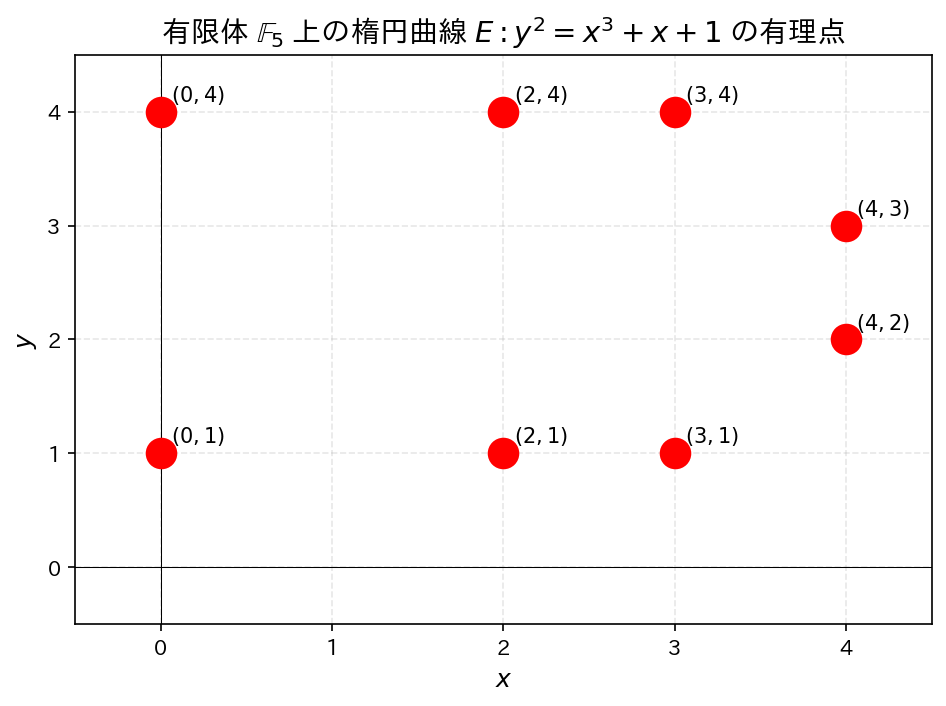
$n \geq 2$ の場合については、Sagemathを使って計算してみると次のようになります：

$\# E(\mathbb{F}_{5^2}) = 27$

$\# E(\mathbb{F}_{5^3}) = 108$

$\# E(\mathbb{F}_{5^4}) = 675$

$\# E(\mathbb{F}_{5^5}) = 3069$

2. 合同ゼータ関数 $Z(E, T)$ の計算

$E$ の合同ゼータ関数

$\displaystyle Z(E, T) = \exp \left(\sum_{n=1}^{\infty} \frac{\# E(\mathbb{F}_{5^n})}{n} T^n\right) \tag{2}$

を計算したいと思います。

$E$ は楕円曲線なので、種数は $g = 1$ です。また、トーラスの幾何的な性質からベッチ数は

$\begin{cases} b_0 = 1 \\ b_1 = 2 \\ b_2 = 1 \end{cases} \tag{3}$

となるのでした。

したがって、ヴェイユ予想の有理性とベッチ数の関係から

$\displaystyle Z(E, T) = \frac{P_1(T)}{(1 - T) (1 - 5T)} \tag{4}$

が得られます。あとは、分子の二次多項式 $P_1(T)$ を決定すればよいことになります。

また、ヴェイユ予想のリーマン予想類似より

$P_1(T) = (1 - \alpha T) (1 - \beta T) \tag{5}$

と表せて、 $\alpha, \beta$ の絶対値は

$|\alpha| = |\beta| = \sqrt{5} \tag{6}$

となります。二乗すると

$|\alpha|^2 = \alpha \overline{\alpha} = 5 \tag{7}$

と表せます。

式 $(5)$ を展開すると

$P_1(T) = 1 - (\alpha + \beta)T + \alpha\beta T^2 \tag{8}$

と表せることにも注意します。

さらに、ヴェイユ予想の関数等式より

$\displaystyle Z\left(E, \frac{1}{5T}\right) = Z(E, T) \tag{9}$

が成り立ちます。

補足：
元々の関数等式の式では、両辺を結ぶ際の符号は $\pm$ となっており、定理の主張としては「不定」です。
しかしながら、代数曲線であれば、いろいろな事情により符号は $+$ に定まるようです。私も理由はよくわかっていません。

式 $(4)$ に $T = 1 / 5T$ を代入すると

$\displaystyle \begin{align*} Z\left(E, \frac{1}{5T}\right) &= \frac{P_1\left(\dfrac{1}{5T}\right)}{\left(1 - \dfrac{1}{5T}\right) \left(1 - \dfrac{1}{T}\right)} \\ &= \frac{5T^2 P_1\left(\dfrac{1}{5T}\right)}{\left(5T - 1\right) \left(T - 1\right)} \\ &= \frac{5T^2 P_1\left(\dfrac{1}{5T}\right)}{\left(1 - 5T\right) \left(1 - T\right)} \end{align*}$

が得られます。

これが関数等式 $(9)$ により $Z(E, T) = \dfrac{P_1(T)}{(1 - T) (1 - 5T)}$ に等しいことから

$\displaystyle 5T^2 P_1\left(\dfrac{1}{5T}\right) = P_1(T) \tag{10}$

が得られます。

ここで式 $(8)$ すなわち $P_1(T) = 1 - (\alpha + \beta)T + \alpha\beta T^2$ を用いて左辺を展開すると

$\displaystyle \begin{align*} 5T^2 P_1\left(\dfrac{1}{5T}\right) &= 5T^2 \left(1 - (\alpha + \beta) \dfrac{1}{5T} + \alpha\beta \dfrac{1}{25T^2} \right) \\ &= 5T^2 - (\alpha + \beta) T + \dfrac{\alpha\beta}{5} \end{align*}$

が成り立ちます。これが $P_1(T)$ と等しいことから、係数を比較して

$\alpha \beta = 5 \tag{11}$

が成り立ちます。式 $(7)$ と式 $(11)$ より

$\beta = \overline{\alpha}$

も従います。

さて、あと $\alpha + \beta$ が分かれば $P_1(T)$ の係数が定まることになりますが、これは前回の記事で得られた式 $(11)$ をそのまま使います。すなわち

$\# E(\mathbb{F}_{5^n}) = 5^n + 1 - \alpha^n - \beta^n \tag{12}$

が成り立ちます。

$n = 1$ のとき

$\# E(\mathbb{F}_{5}) = 5 + 1 - \alpha - \beta$

なので、移項して

$\alpha + \beta = 6 - \# E(\mathbb{F}_{5})$

となります。

ここで、 $E$ の $\mathbb{F}_5$ -有理点の個数は $\# E(\mathbb{F}_5) = 9$ だったので、

$\alpha + \beta = 6 - 9 = -3 \tag{13}$

となります。

以上により、式 $(11)$ と式 $(13)$ から $P_1(T)$ の係数がすべて定まり、合同ゼータ関数が

$\displaystyle Z(E, T) = \frac{1 + 3T + 5T^2}{(1 - T)(1 - 5T)} \tag{14}$

と求まりました。

ここで、 $P_1(T)$ を因数分解すると

$1 + 3T + 5T^2 = \left(1 - \dfrac{-3 - \sqrt{-11}}{2} T\right)\left(1 - \dfrac{-3 + \sqrt{-11}}{2} T\right)$

と表されるので、 $\alpha, \beta$ は

$\displaystyle \alpha = \dfrac{-3 - \sqrt{-11}}{2}, \;\; \beta = \dfrac{-3 + \sqrt{-11}}{2} \tag{15}$

と求められます。

これらの絶対値は

$\begin{align*} |\alpha|^2 = |\beta|^2 &= \dfrac{-3 - \sqrt{-11}}{2}\cdot \dfrac{-3 + \sqrt{-11}}{2} \\ &= \dfrac{9 - (-11)}{4} = 5 \end{align*}$

より

$|\alpha| = |\beta| = \sqrt{5}$

となり、ヴェイユ予想のリーマン予想部分が成り立つことが確認できました。

3. 合同ゼータ関数の形から有理点の個数が分かる

以上から、 $\mathbb{F}_{5^n}$ 上の有理点の個数は

$\displaystyle \# E(\mathbb{F}_{5^n}) = 5^n + 1 - \left(\dfrac{-3 - \sqrt{-11}}{2}\right)^n - \left(\dfrac{-3 + \sqrt{-11}}{2}\right)^n \tag{16}$

と表せることが分かりました。この公式が本日の結論1です。

この公式から

$\# E(\mathbb{F}_{5^2}), \; \# E(\mathbb{F}_{5^3}), \; \# E(\mathbb{F}_{5^4}), \; \# E(\mathbb{F}_{5^5}), \; \ldots$

がすべて計算できます。

実際、 $n = 2$ のときは、

$\displaystyle \begin{align*} \# E(\mathbb{F}_{5^2}) &= 5^2 + 1 - \left(\dfrac{-3 - \sqrt{-11}}{2}\right)^2 - \left(\dfrac{-3 + \sqrt{-11}}{2}\right)^2 \\ &= 26 - \left(\dfrac{-1 - 3\sqrt{-11}}{2}\right) - \left(\dfrac{-1 + 3\sqrt{-11}}{2}\right) \\ &= 26 - (-1) \\ &= 27 \end{align*}$

と計算できます。これは上で数値計算で求めた $\# E(\mathbb{F}_{5^2}) = 27$ と一致しています。

$n = 3$ のときは

$\displaystyle \begin{align*} \# E(\mathbb{F}_{5^3}) &= 5^3 + 1 - \left(\dfrac{-3 - \sqrt{-11}}{2}\right)^3 - \left(\dfrac{-3 + \sqrt{-11}}{2}\right)^3 \\ &= 126 - \left(9 + 2\sqrt{-11}\right) - \left(9 - 2\sqrt{-11}\right) \\ &= 126 - 18 \\ &= 108 \end{align*}$