一つ前の記事で「LTEの補題（指数持ち上げ補題）」という有名な補題について勉強しました。せっかくなので、この補題を何か他のネタにも使えないかと考えました。
LTEの補題とは、こんな主張の補題でした：
これ自体の証明は、たとえば INTEGERSの記事 をご覧になってください。
色々考えていくうちに、レピュニットに応用できそうだ というところに思い至ったので、そのことについてまとめたのがこちらの記事です。
今回紹介するレピュニットの性質については、なかなか面白いと思います！ なにせ、私はこの性質が載っているサイトを見たことがありません。
よかったらぜひ楽しんでいってください！
世の中の現象の中には「ランダム」な現象が多々あります。たとえば、サイコロを振るのは分かりやすいランダムな現象の例です。他にも天気や地震、ギャンブルなども分かりやすいランダムな現象の例です。
一方で、コンピュータの中で行われる計算は、一定のアルゴリズムにより定められた計算が順次実行されることになるため、原理的にはランダムになることはありません。
このことはコンピュータ内でランダムな現象をシミュレーションするにあたって問題になります。そこで「決められた手順によって生成されるランダムっぽく振る舞う数列」をいかにして作るかが重要になるわけですね。このような数列を擬似乱数と言います。
コンピュータによって擬似乱数を生成する手法は、これまでもさまざまな手法が提案されています。今回は、その中でも特に有名な手法である 線形合同法 について考えたいと思います。
最近はもっと良い疑似乱数の生成法が発見されているので、線形合同法はあまり使われていないと聞きます。しかし、一昔前のC言語等の乱数生成には、この方法が普通に使われていました。
簡単に線形合同法について説明しましょう。線形合同法とは次のようなアルゴリズムです。
を
であるような整数とし、整数
を次の漸化式によって定めます：
ただし、 は
の中からとることにします。
このように数列 を選ぶと、
を決める毎に異なる疑似乱数の列が得られるというわけです。
たとえば、 とします。このとき、
とすると
のように数列 が得られます。
今回の数列は結構優秀で、数列をこのまま続けていくと、こうなるのですが・・・
実は、 からスタートして
に戻ってくるまで、
から
までの数がすべて１回ずつ出力されています。つまり、この数列の周期は
というわけですね。周期は法
を超えることはないので、これが最大周期になります。
パラメータ によっては最大周期とならないケースも存在します。たとえば、
とすると
となりますが、これは が繰り返されるので、周期
となります。
あとで述べるように、一般に線形合同法によって得られる数列は周期 を持ち、その周期は
となります。
今回のメインテーマは、パラメータ がどのような条件のとき周期最大（
）となるのか、という問題です。周期は長ければ長いほど疑似乱数としては優秀だと考えられるので、気になる問題設定です。
線形合同法において最大周期になる必要十分条件は知られていて、以下の定理1が成り立ちます。
実際、 のケースでは、条件 (i), (ii), (iii) を満たすので最大周期
になったというわけですね。
しかし、一体どうしてこのような必要十分条件になるのか気になりますね。そこで、今回の記事は 定理1を証明 してみたいと思います。
自力で考えてみてもなかなか難しかったので、証明がどこかに載っていないか調べてみましたが、ネット上で一般的なケースについての証明は見かけませんでした。
その後、Knuth先生の "The Art of Computer Programming Volume2 Seminumerical Algorithms" に証明が載っていることを知り、今回参考にさせていただきました。
しかしながら、証明を読んでいて納得いかない部分がいくつかありました。
こちらの記事では、大枠の証明は上記に従いつつも、いくらか自分流に修正したものをまとめたいと思います。
続きを読む今日は5月12日なので 512 の日ですね！
なので、2のべき乗で表せる数というわけです！嬉しいですね！（え、嬉しくないですか？）
楽しくなってきたので他にも面白い性質ないかなと、Wikipediaの「512」という項目を調べてみると、次のような性質を見つけました。
（
）で表せる24番目の数である。1つ前は500、次は625。(オンライン整数列大辞典の数列 A003592)
なるほど
と書けるので、 で表せる数ということですね。
・・・ 関係ないですやん。
この性質に何の意味があるんだろう・・・。このWikipediaの記事を書いた人は、どういう気持ちでこの性質を追加したのだろう・・・。
このままでは512がかわいそうなので（？）、 で表せる数に何か数学的な意味を見出してあげたいですね。
そこで私が思いついたのは
という分数についてです。
続きを読むいつもブログを読んでくださってありがとうございます！
今日５月９日は私の誕生日なのですが、今年で３６歳を迎えまして「平方数歳」になりました。おかげさまで今年も楽しく数学をできています！
せっかくの３６という年齢なので、３６にまつわる何かをしたいですね。何かアイデアある方いましたら、ぜひコメント欄かTwitterで教えてください。
さて、今日は２つほどお知らせがあるのですが、その一つ目が テレビ出演 についてです。
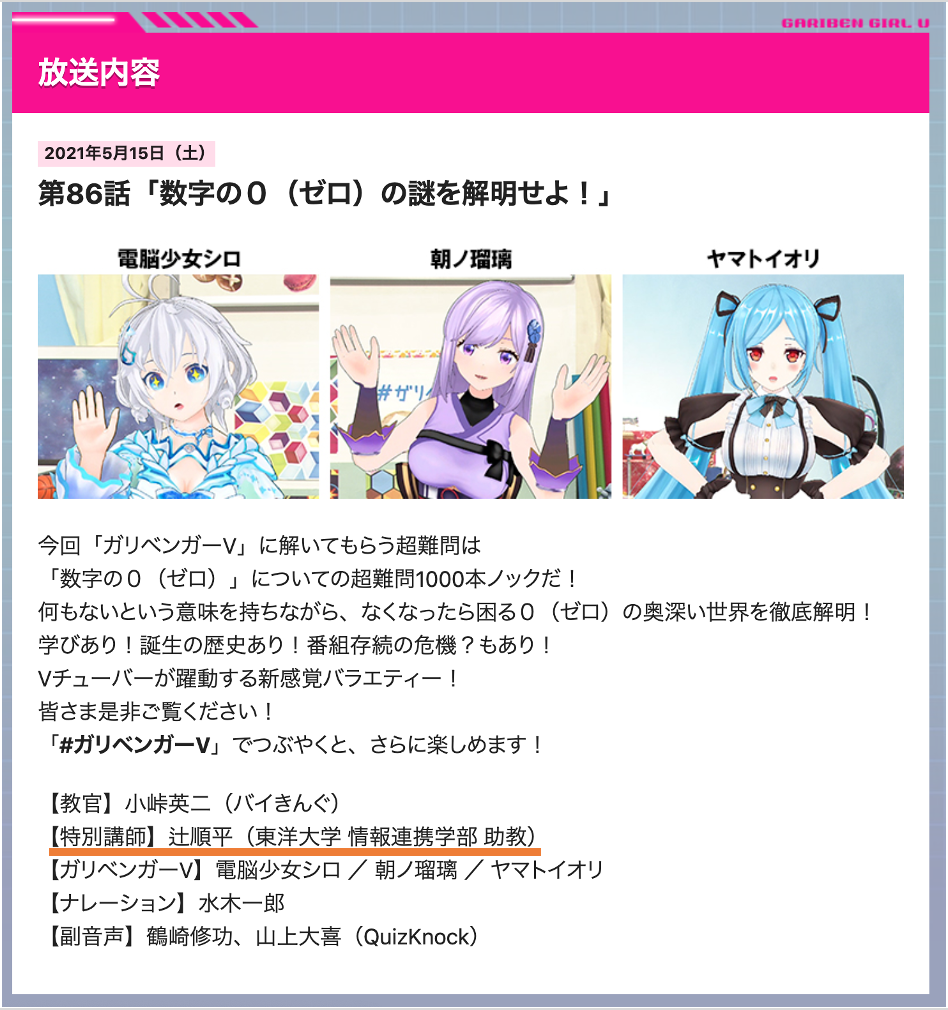
テレビ朝日の ガリベンガーV という番組に出演することになりました。
ガリベンガーVという番組は、最近流行りのVTuberが出演して、わいわい楽しく科学的なトピックを勉強するという番組です。tsujimotterはもちろんVTuberとして・・・ではなく特別講師の方で出演させていただきます。
今回のテーマは 「数字０（ゼロ）」 です！
これまで85回ほど色んなテーマを紹介してきた番組ですが、数学の回は「今回が初めて」とのことです。そんな特別な回に講師として呼んでいただきました。
来週5/15（土）の深夜24時5分 に放送されます！
（土曜から日曜に変わる瞬間の時間です。）
テレビをお持ちでない方も（私も持っていないｗ）TVerというサイトで、放送直後から（無料で）見ることができます。便利な世の中になったものですね！
ぜひご覧になってください！
www.tv-asahi.co.jp
Twitterのハッシュタグ #ガリベンガーV で実況などしていただけると、大変喜びます！
裏話などは、また放送後に紹介できればと思っています。当日はVTuberのみなさんが（びっくりするぐらい）楽しそうに聞いてくださったので、私としてはとても楽しい気分で話せた収録でした。どんな形で放送されるかはわからないですが、これまでの放送の様子を見るにきっと楽しくまとめてくださると思います。お楽しみに！
もう一つのお知らせが、表現者のための数学 という数学の講座についてです。
peatix.com
【以前の申し込みページで申し込まれた方へ：手違いにより元のイベント申込ページが削除されてしまいました。お手数ですが、返金の完了を確認の上、再度こちらよりお申込いただけますでしょうか。】
キュレーターの高橋裕行さん、ピタゴラスイッチ等に携われた星功基さんのお二人と私の三人で、やさしく楽しく大学数学の初歩に親しむ講座を企画することになりました。
元々、高橋さんから「文系の人にわかるように群論について教えて欲しい」というリクエストがあり、群論の勉強会を開こうとなったのがきっかけです。人文科学でもレヴィ=ストロースの「親族の基本構造」など、群論を応用した研究があり、そういった事例が見聞きして群論に興味を持ったとのことです。
せっかく準備して話すなら、高橋さんだけでなくさまざまなバックグラウンドを持った方に対しても大学数学に親しむ機会を提供できるのではと思い、オープンなオンライン講座とすることになりました。
参加者としては次のような人たちを想定しています。
数学の専門的な話を勉強したい方向けの講座ではないので、その点はご注意ください。あくまで群論の初歩的なところに触れてみたい方向けの講座となっています。
今回のテーマ「群論」では、月１回ずつの３回に渡る講座となっていますが、5/13（木）の第１回 の内容は次のような話になりそうです。
1. なぜ「群」を学ぶのか？
2. キーワードは「対称性」？
3. 身近な対称性
4. 「対称性」から「群」へ（本日のメインパート）
5. 「巡回群」を探してみよう！
第２回では、巡回群以外の群や、もう少しだけ突っ込んだ群論の概念を紹介し、さらに群論の応用として上で触れたレヴィ=ストロースの事例や、音楽理論への事例などを紹介する予定です。
今回の講座の特色としては、単に群論の勉強をするというだけではなく、それを何かしらの表現活動（アート・デザイン・作曲・プログラミング・スポーツ・料理・文章執筆・動画制作 etc.）に活かしていただくというところにあります。
実際、第２回で紹介するように、群にはさまざまな分野への応用があります。また、群論そのものを使わずとも、そこで登場する「対称性」「可換・非可換」などのアイデアや、ものごとを抽象的に捉えて「異なるものを同じものとみなす思考」などは、さまざまな表現に応用できるものだと思います。
そこで第３回では、参加者のみなさんに群論のアイデアを使った「作品」を作っていただき、「課題発表会」でその内容を紹介していただこうと考えています。さまざまなバックグラウンドの参加者のアイデアを見ることで、より広い視野が得られるような会になることを期待しています。
tsujimotterは第１回に向けて絶賛準備中です。今の所かなり面白い講座になるのではないかという実感があります。まだ参加者は募集しています。みなさまのご参加をお待ちしております。
peatix.com
【以前の申し込みページで申し込まれた方へ：手違いにより元のイベント申込ページが削除されてしまいました。お手数ですが、返金の完了を確認の上、再度こちらよりお申込いただけますでしょうか。】
それでは今日はこの辺で！
モジュラー曲線というのは、上半平面 を
の合同部分群で割ったものとして定義されます。
定義からは、明らかに複素解析的な対象に見えると思います。ところが、実はモジュラー曲線は数論的な対象でもあるのです。
わかりやすい応用として、楕円曲線の位数有限な点に関する メイザーの定理 があります。
これは楕円曲線の有理点の構造を決定するために大変有用な定理です。数論における大定理といってよいと思うのですが、この定理を証明するのにモジュラー曲線が用いられるのです。
メイザーの定理の証明自体は私は理解できていないので、ここでは解説はできません。今回は、位数有限の有理点とモジュラー曲線の関係に限って紹介したいという記事です。
話のキーとなるのは、モジュラー曲線の一点一点が楕円曲線の同型類に対応する という事実です。つまり、モジュラー曲線は楕円曲線の モジュライ空間 であるのです。
また、モジュラー曲線のもう一つの側面として、代数曲線としての性質があります。具体的に、方程式のなす点集合として表すことができるのです。この曲線としての性質から、たとえば位数Nの有理点を持つ楕円曲線が存在しないことが言えてしまうのです。
そんなわけでモジュラー曲線のすごさをお伝えしたいと思います。
また「モジュラー曲線」シリーズの過去記事はこちらで読むことができます：
tsujimotter.hatenablog.com
今回の記事はシリーズ記事ですが、前回（モジュラー曲線(4)）からずいぶんと時間が経ってしまいましたので、この記事単体で読めるような記事にしたいと思います。そのため、過去の記事と重複する部分もかなりあるかと思います。必要に応じて過去の記事を参照してみてください。
４年に一度、国際数学者会議（ICM: International Congress of Mathematicians）と呼ばれる大きな催しが行われます。フィールズ賞という、数学界の最高峰の賞が発表される会としても知られていますね。
次回、2022年にはロシアのサンクトペテルブルグにてICM 2022が開催されるようです。私がこの情報を知ったのは、ICM 2022の公式が出しているプロモーション企画の情報を、Springerさんのツイート経由で見たのがきっかけでした。
プロモーション企画のタイトルは "Surprising math user video contest" です。いかにも楽しそうなタイトルですね！
企画のページはこちらです：
icm2022.org
要するに、数学に関する面白い動画を投稿するコンテストのようですね。我こそはという方は挑戦してみてはいかがでしょうか。
特に見ていただきたいのは、ICM 2022公式が出している宣伝動画です。
www.youtube.com
動画を見てまず感じるのは、映像に登場する図がとてもきれいだということですね。それだけでもそそられますが、内容も大変面白く、私の心に深く刺さりました。
とはいえ、企画のプロモーション動画ということもあり、時間は短めで、かつ音声による説明はまったくありません。内容自体も結構高度なので、背景知識がないとなかなか理解するのは難しいかと思います。
そこで今回は、あくまで私の理解できた範囲で、このICMの動画の内容の解説を試みたいと思います。もちろん、私も１００％理解できているわけではないので、あやふやな点も多々あるかと思います。その点をご了承の上、見ていただけると嬉しいです。
テーマは
です。大変面白いトピックなので、ぜひ最後まで読んでいただきたいです！
続きを読む
