前回の内容を簡単に振り返ります。「空間内の与えられた2直線 に対して、その距離を求めることはできるか?」という問題について考えました。
からそれぞれ点
をとったとき、
の距離は2変数の2次関数関数
として求められます。
の最小値を求めれば、
の距離が求まるという話でした。
ここで「2変数の2次関数の最小値はあるのか?」という部分が一つの焦点だったわけですが、 が平行でない場合には最小値が極小値に一致する(最小値は存在する)という結論でした。
上の記事では、 を力技で平方完成して最小値を出していました。ところが、ブログ公開後にTwitter上で @Freufirst さんという方から「2次関数の平方完成は合同変換で出来るよ」という旨のアドバイスをいただきました。教えていただいた方法は「まさに」という方法だったのですが、昨日の時点ではまったく頭にありませんでした。ありがとうございます。
というわけで、せっかくなので行列を使った2変数2次関数の極値問題の解法について、詳しくまとめてみたいと思います。2変数2次関数 が極小値(あるいは極大値など)を持つ条件について考察していきたいと思います。
今回は、行列やベクトルとしての式変形を用いてスマートに求めることを目指します。計算の途中では、いくつかの「行列やベクトルの変換操作」を行っていきますが、それらは単なる機械的な置き換えではなく、実はちゃんと図形的な意味があるものになっています。記事の後半では、そのことについても触れていきたいと思います。
目次:
2変数2次関数の行列を使った表示
2変数2次関数 の一般形を
と表しておきます。この関数が極小値を持つか、持つのであればどの点 でが極小値を持つのか、というのが知りたい問題でした。
ここで、次のような行列とベクトルをおきます:
添え字の は行列の転置(行と列を入れ替える)記号です。基本のベクトルが縦ベクトルになるように、最初から転置記号を当てて定義しています。
このようにすると、2次関数 は
とかけることになります。
特に、 の部分は 2次形式 と呼ばれる部分ですね。
このようにまとめておくことで、式自体がすっきりまとまっていて見通しが良くなります。また、次に述べるように平方完成の計算が著しく簡単になります。
もう一つのメリットとしては、今回の計算をそのまま一般の 元2次形式でも実行できるという点ですね。今回はやらないですが。
平方完成
ここで、ベクトル変数 の部分が1項目と2項目に別れてしまっているのが気になると思います。これを一つにまとめましょう。これがまさに「平方完成」に相当する計算です。
結論から言ってしまうと、次のような変数の置換を行います:
ここで、両辺の転置をとると
となります。
の計算ですが、 まず行列の積の転置
を用いています。また、 であり、
は対称行列(転置をとっても変わらない)なので、
となります。
これらを2次関数の式 に代入しましょう。すると
ここで、一見異なる二つの式 と
ですが、結果がスカラーとなり互いに転置の関係にあるので、実は同じ式です。これを使うと
となり、ばっさりと項が消えていきます。結果的に
が得られます。
あんなに難しかった平方完成が、こんなに簡単に出来るなんて・・・。中身の値を気にせず行列のまま計算を進めることができるのが嬉しいですね。これが行列計算の良さなのかなと思います。
対角化と主軸変換
そんなわけで「2次の項」と「定数項」にきれいに分離できたわけですが、もう少しだけ変形することができます。
としては実対称行列を仮定しています。ここで線形代数の一般論により、
は直交行列
を用いて対角化可能です。すなわち
となります。ここで、 は行列
の固有値です。
そこで、対角化に用いた直交行列 を用いて変数変換
を施すことを考えます。このような変換を「主軸変換」といいますが、その意味は次の節でわかるかと思います。
転置をとると
ですが、直交行列の定義より が成り立ちます。
したがって、式 に代入すると
となります。
これによって、2次形式 の行列部分
が対角行列になりました。これの何が嬉しいのでしょうか。
2次形式を改めて展開すると、その良さが実感できるかと思います。 とおくと
となります。定数項を一旦忘れると となります。これはもうめちゃめちゃ簡単な式になっていますね。
であれば極小値をただ一つ持つことが、見れば明らかです。
は行列
の固有値でしたが、こんな風に行列の固有値がすべて正になる行列を正定値(positive definite)であるといいます。このときは極小値を持つというわけですね。
また、 がどちらも負である場合は、負定値(negative definite)といいます。この場合はただ一つの極大値を持つわけですね。
面白いのは、 のような状況です。この場合は、
方向には増大していくが、
方向には減少していくような挙動となります。こういう状況を鞍点(suddle point)といいます。
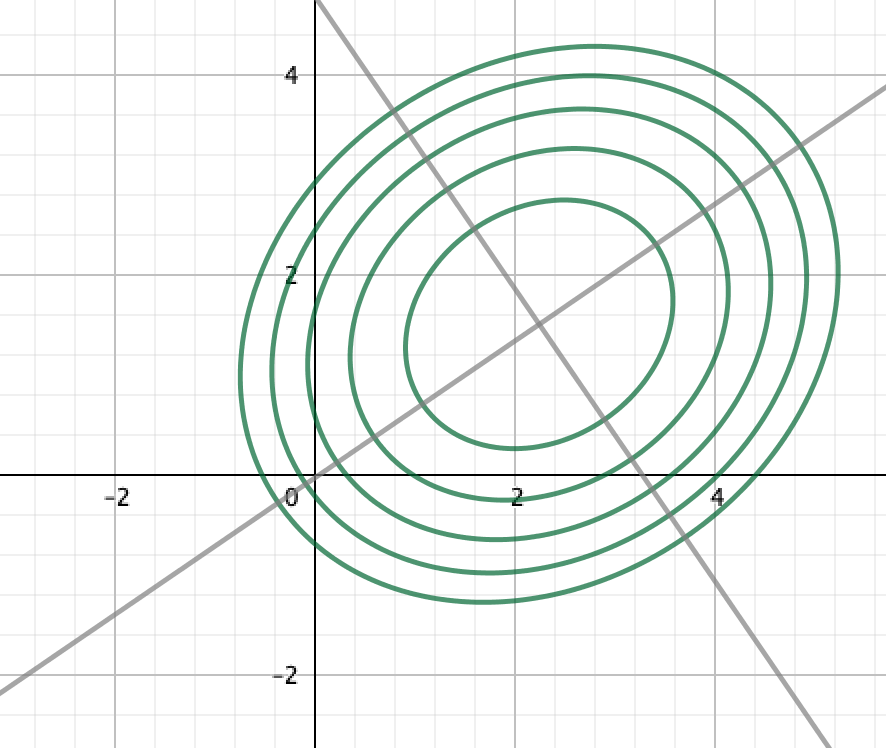
主な挙動として3通りの状況を図示します。
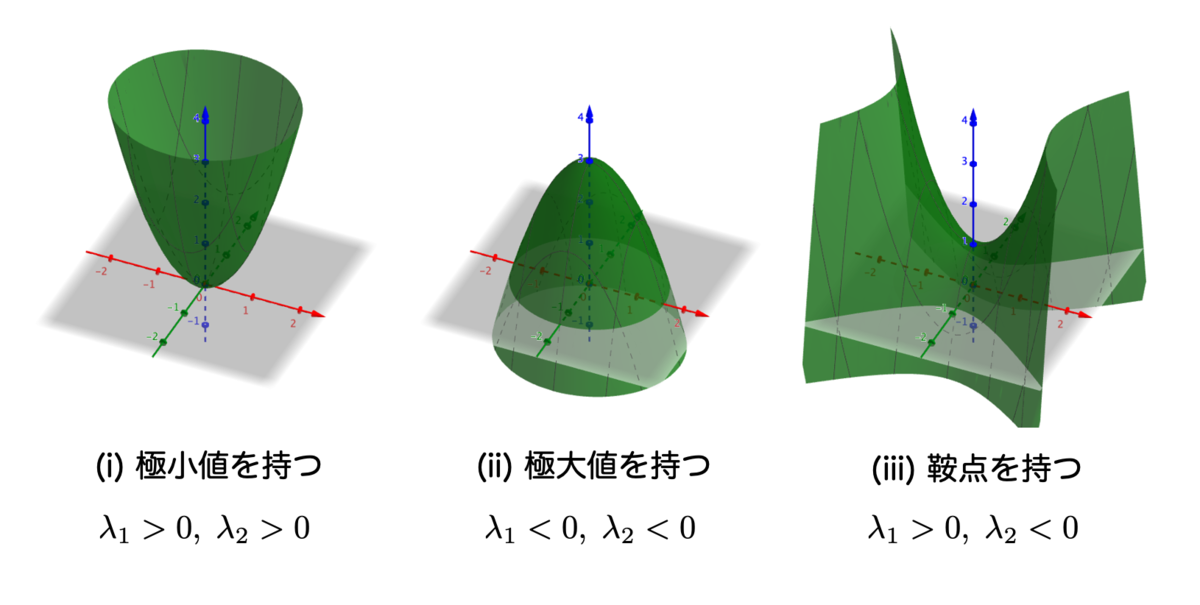
もちろん、これら以外の状況も存在して、たとえば固有値が になるときは非常にややこしいことになります。
なお、前回の問題に照らしあわせると、2本の直線が平行でない場合は、正定値行列になるので はただ一つの極小値を持つというわけですね。
これまでの変換の図形的な意味
極小値を求めるにあたって2つの変換を施してきたわけですが、最後にこれらの変換の図形的な意味を説明して終わりたいと思います。
(
は対称行列)
(
は
を対角化する直交行列)
逆順に進んでいったほうがわかりやすいかと思いますので、変数 からスタートします。
が正定値のとき、変数
に関する2次関数
は、原点にただ1つの極小値を持つ関数でした。関数の概形としては「すり鉢状」の形をしているわけですね。
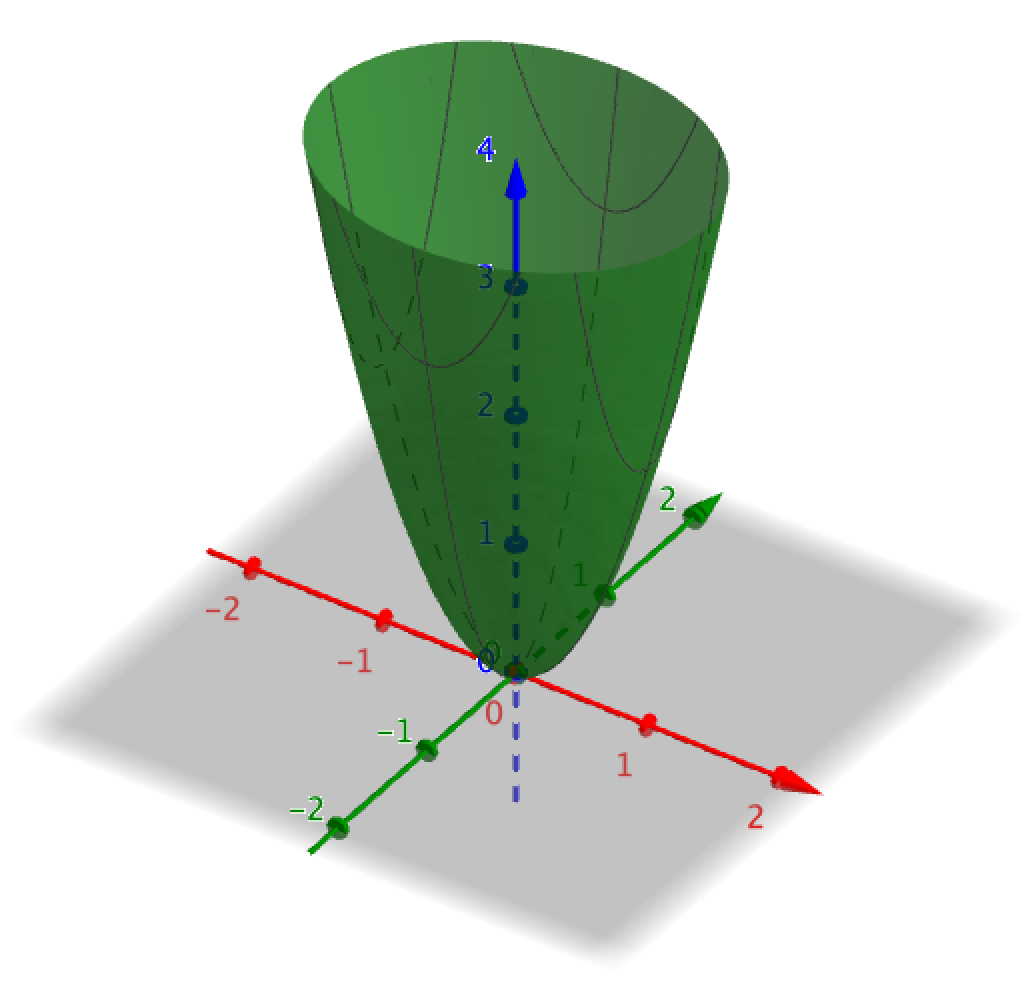
3Dの図形を思い浮かべながら、説明の方では関数の「等高線」を用いて説明したいと思います。
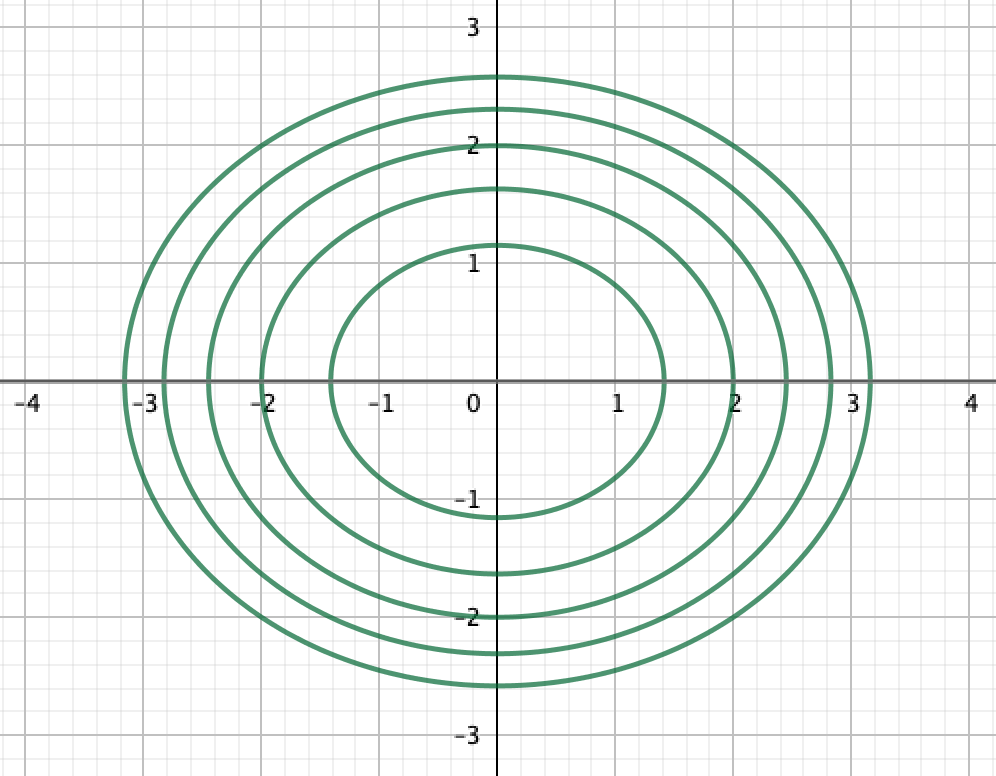
等高線がすべて楕円になっていることがポイントです。楕円の長軸と短軸が のいずれか一方に対応していて、それぞれ軸の長さが
に対応しているわけですね。
さて、これに対して、 なる変換を施すとどうなるでしょうか。
は直交行列でしたが、2次の直交行列の意味するところは「回転」または「鏡映」です。
軸を回転したり鏡映したりする座標変換というわけですね。
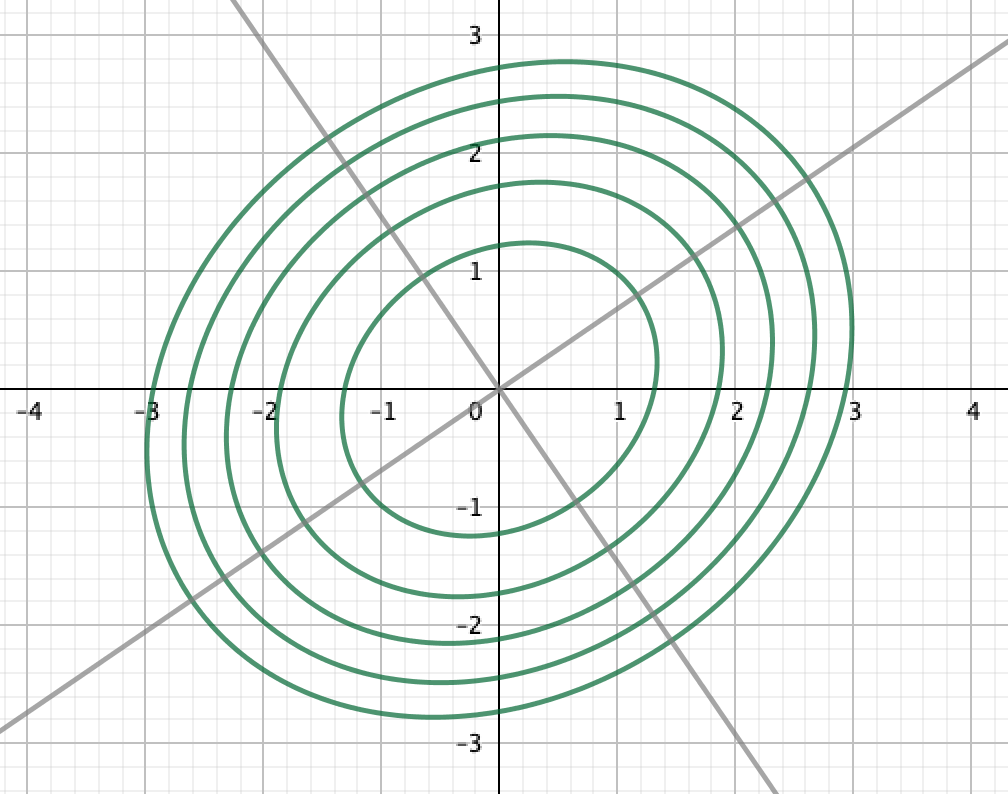
先ほどこの変換を「主軸変換」と言いましたが、これで意味はわかったのではないでしょうか。「主軸」を「変換」していますよね。
逆に考えると、元々の 座標においては、「原点を通る2本の軸」に沿って等高線の楕円の「長軸」と「短軸」が伸びていたわけです。これらを「主軸」といいます。これが主軸変換(
座標から
座標への変換)によって、直交する横と縦の軸に置き換わったということになりますね。行列の対角化というのは、まさにこういう幾何的な意味があったというわけです。
また、この変換の際に 座標での2次形式
から 座標での2次形式
へと変換が行われています。つまり、行列を対角化することは、2次形式でいうところの真ん中の項( の項)を消すことに他ならないというわけですね。
最後に、 という変換についてですが、これは簡単ですね。ベクトル
にベクトル
を足して新たな座標
としているわけです。ただの「平行移動」ですね。
つまり、「平方完成」には極小値を原点に移す「平行移動」の役割があった というわけですね。こうやって聞くと確かに1変数のときの平方完成もそうだったなと思いますね。
そんなわけで、それぞれの変換についての幾何的な意味をまとめると
- 平方完成: 極値を原点に移す平行移動
- 主軸変換: 等高線の長軸と短軸(主軸)の向きを変える(直交する軸に変換する)
ということになるかなと思います。「平行移動」と「回転(or鏡映)」の組み合わせなので「合同変換」ということですね。面白いですね!
それでは今日はこの辺で!
おまけ:正定値になる条件
正定値という条件が出てきたので「正定値になる条件」について考えてみましょう。実際、行列が正定値、すなわち「固有値が正である」という条件は、少し直感的ではないですよね。
極小値を持つ条件なので、以降 は仮定しておきます。
ここで、 としておいて、行列
の固有値を考えます。
の固有値は、あるベクトル
が存在して
を満たすような のことでした。
は実対称行列なので、すべての固有値は実数になることに注意します。
単位行列を とすると
を満たすという を求める問題となります。このとき、行列
は退化していますので、行列式が
となります。したがって
が成り立ちます。これは についての2次方程式となっていて、左辺を固有多項式といったりしますね。
固有多項式を変形すると
ということになります。
ここで、もし であれば
となります。今、 なので、
の範囲は
ということになります。
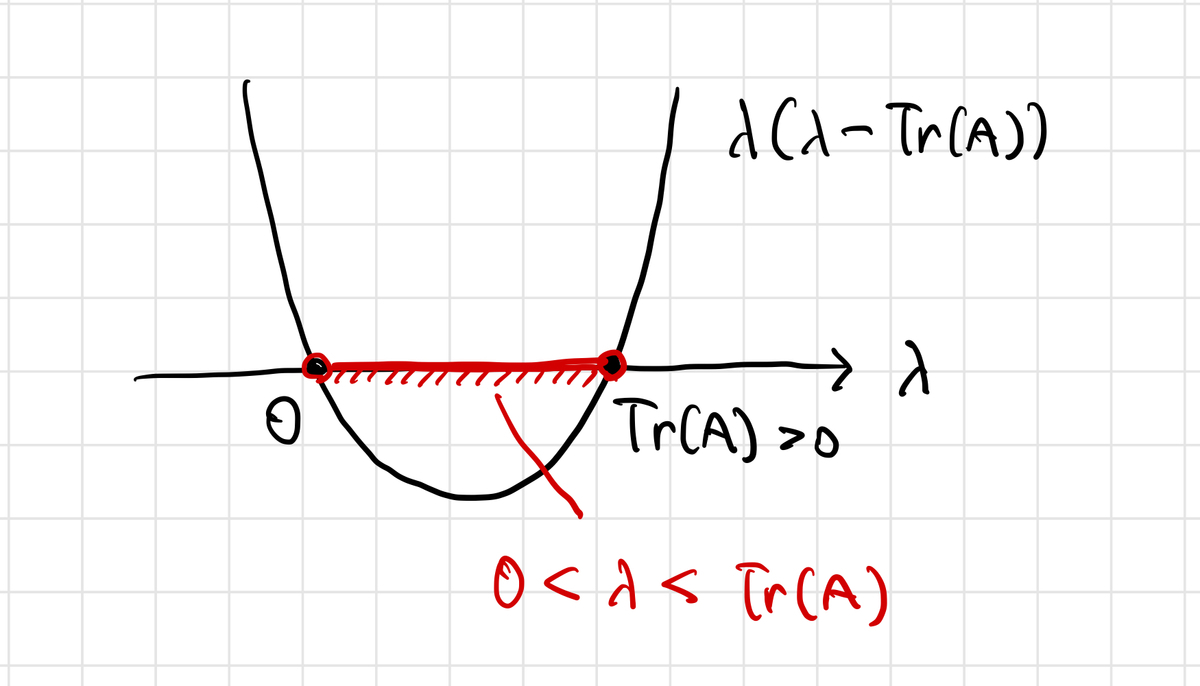
すなわち、 は常に正の値をとるということです。これは行列
が正定値であることを意味します。
よって、前回と同様の結論が得られることになります。
結局、前回やったような「 のヘッセ行列の行列式
が正である」という条件がそのまま出てくるわけですね。実際、
のヘッセ行列は、
を偏微分してみることで
であることがわかります。なるほどそれはその通りという感じですね。