Twitterで数学に関するこんな話が話題になっていました。
√-2×√-8計算する時に√16にしたらいけんのなんで?
— 愛華 (@sakubunkake) 2020年7月9日
もう少しツイートの内容を補足してみましょう。 というのは、虚数単位
を用いて
として定義されます。よって を用いて
が成り立ちます。
一方、 には積に関して
なる法則が成り立つはずです。
ところが、この法則を適用すると
となってしまいます。
すなわち、計算方法によって結果が になったり
になったり、異なってしまっています。これは何かがおかしい。一体、どこがおかしいのだ?
というのが、上のツイートが問題にしている点です。
私はこのツイートを見て、これは モノドロミー の問題だ!
と直感しました。これは面白そうだと。
そこで、以前書いたこの記事
tsujimotter.hatenablog.com
を思い出しながら、自分でも考えてみることにしました。
私の中ではかなり納得感のある結論にたどり着きましたのでまとめてみたいと思います。よかったら聞いてください。
元々のツイートは高校生の方のものだと思われますが、本記事は「高校生に向けた解説記事」というわけではありません。
あくまで、趣味で数学を勉強する筆者(日曜数学者)が、自分で考えているうちに楽しくなってしまい、まとめてみたくなったというタイプの記事となっています。
この点にご留意して読んでいただければと思います。
色々検討した結果、第4パートと追記のところでリーマン面上の点に対して積をとっている箇所が怪しい議論をしていると感じています。記事修正が困難なためそのままになっていますが、鵜呑みにせず話半分に読んでいただければと思います。
第1〜第3パートについては、通常の複素関数論と同様の議論だと思いますので、今のところ問題ないと思います。
1. 正の数の平方根
「そもそも平方根の定義とは何だったのか?」というところから思い出したいと思います。
を実数とし、実数
を
の
乗とします。すなわち
が成り立つということです。このとき、 も
乗すると
に一致します。つまり
ということですね。
このとき、 と
は
の 平方根 といいます。
つまり、 の平方根というやつは、定義からして 2つ 存在するわけですね。
ところで、 の
と
は実数なので大小関係があり、どちらか一方が正の数になります。そこで、
の平方根の2つのうち正の方 を特別に
と表す ことにします。これにより、
の2つの平方根を
と表すことができるわけです。これが という記号の定義です。
高校までに、こんなややこしいことを習っていたのですね。
みなさん覚えていました? tsujimotterは忘れていました。
まとめると、 のとき、
の平方根は2つあるわけですが、 そのうち正の方を選んで、
と名付けているというわけでした。
「正の方を選んで」と強調しているのは、選べない例があるからなのですが、それについてこれから説明していきたいと思います。
後の議論を踏まえて、今の状況を複素数平面によって図示しておきたいと思います。以降、複素数全体の集合を で表すことにします。
は正の実数、
も実数としていましたが、複素数平面における実軸上の点だと思うことにしましょう。
乗する写像
によって、
にうつる様子を表したのが次の図です:
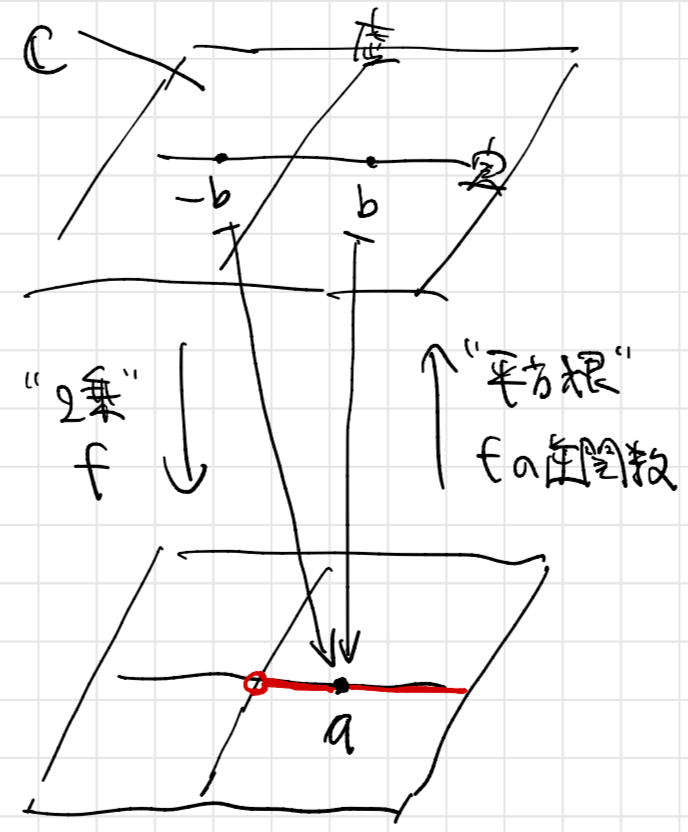
このように表すと、平方根は の逆関数であることが分かりますね。
ただし、逆関数の値は に対して1つには定まりませんので、正の方を対応させることにして、それを
と名付けるというわけです。
2. 負の数の平方根
それでは負の数 の平方根についても考えてみましょう。
虚数単位を として、純虚数
と
を考えます(
は実数とします)。するとこれらを2乗したものは同じ数
に一致しますね。ここで とおくと、負の実数
の平方根は
の2つであるということができます。
先ほどの複素数平面の写像を考えると、虚軸上の2点 から
乗写像
によって
にうつっていることがわかります。

ここで の逆関数として
を考えたいわけですが、ここで困ったことが。
は
と
のどちらに対応づければ良いでしょうか?
どっちかに決めなければいけませんが、一般には
とすることが多いかと思います。つまり、 と
のうち、係数
が正である方を選んだということですね。
というように言い換えてもいいかもしれません(こっちの方が一般的な定義の仕方ですね)。
つまり、 の係数が正の実数になるように 「えいっ」 と決めたというわけです。
いや、ほんとにそうで、特に決め手がないので「えいっ」と決めるしかないのです。
こういう風に、平方根のどちらかを「えいっ」と定めることを、専門用語で 分枝を決める といいます。
ともあれこれで、正の実数と負の実数 に対して、
を一意的に定めることができました。
3. 複素数の平方根とリーマン面
そうなってくると、一般の複素数 に対して、
を考えたくなります。しかし、これが一筋縄ではいきません。
先ほどは、えいっと決めることができましたが、今度はそういう風に決める手立てがないのです。
図では、2つの複素数 によって
と表されている状況を考えます。すなわち、
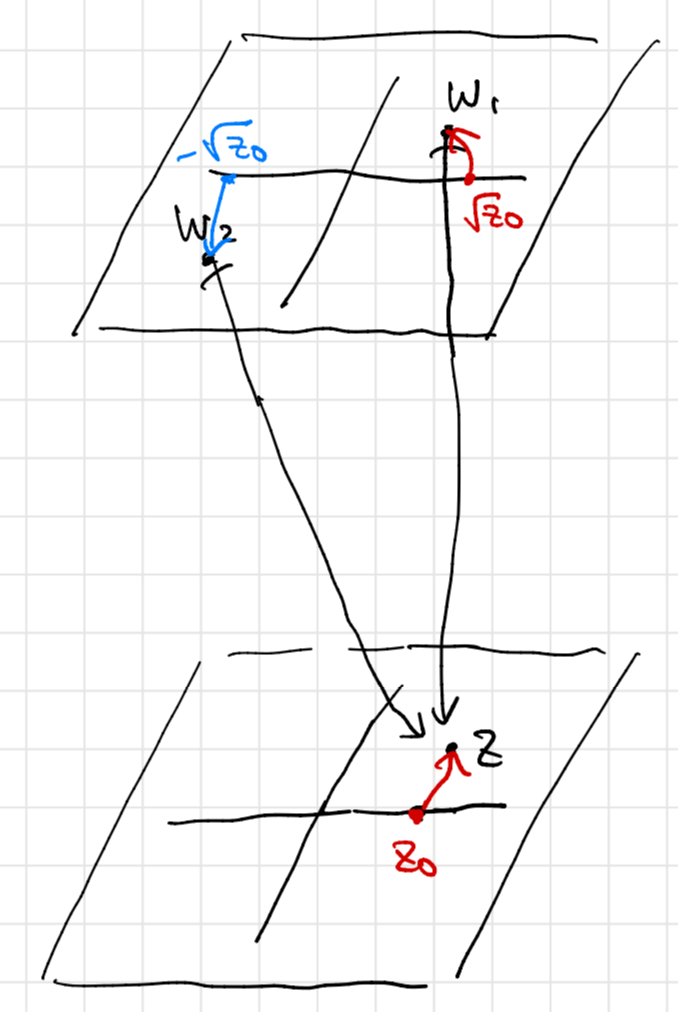
これに対する一つの答えは、 が正の実数である点から始めて、
を連続的に繋いでいく という方法です。
元々 が正の実数のときは、正の平方根
によって
を定めることができるのでした。ということは、
を
から「ちょっとずらした点」とした場合、
は
から「そう大きく離れた値を取らない」と思えそうです。
の候補は2通りありますが、
に近い方を選べば、一つに決められそうです。
こんな要領で、 を正の実数
からスタートして、座標
を「ちょっとずらして」
の値を決定し、また座標を「ちょっとずらして」
の値を決定し、と繰り返し進めていくのです。
このようにして、 を連続的に繋いでいくことができそうです。
すなわち、 という関数は
を中心にテイラー展開できます。同様に
を中心にテイラー展開したものを考えます。双方の展開における収束円に重なりがあれば、一致の定理により、収束円をまたいで二つの関数を解析接続できるわけですね。
これが「 を連続的に繋いでいく」の意味するところです。
こんな感じに、 からスタートし、
を通らずに
の周りを左回りに移動していくことを考えましょう。
が負の実軸上に到達すると、
は
に一致します。こうして先ほどの負の実数の議論が正当化されるわけです。
これでうまくいきそう・・・と思いきや、一つ問題が生じます。
その問題は、 からスタートして、
の周りを左に一周回って
に戻ってきたときに起こります。
なんと、 になってしまうのです。これは驚きです。
のときには、
だったはずなのに、ただ一周して戻ってきただけで関数の値が
と変わってしまうのです。このような現象を モノドロミー といいます。
つまり、 に対して、関数の値が一意に定まらないということです。これが多価関数です。これは困った。
こういう状況のときに使える一つうまい考え方がありまして、それが 定義域を2枚の複素数平面へと拡張してしまう方法 です。
次の図のように複素数平面2枚を左右に用意します。そしてそれぞれの の実軸上に切り込みを入れておきます。この切り込みを使って、2枚の複素数平面を貼り付けてしまうのです。ちょうど、赤い部分同士、青い部分同士がつながるようにします。
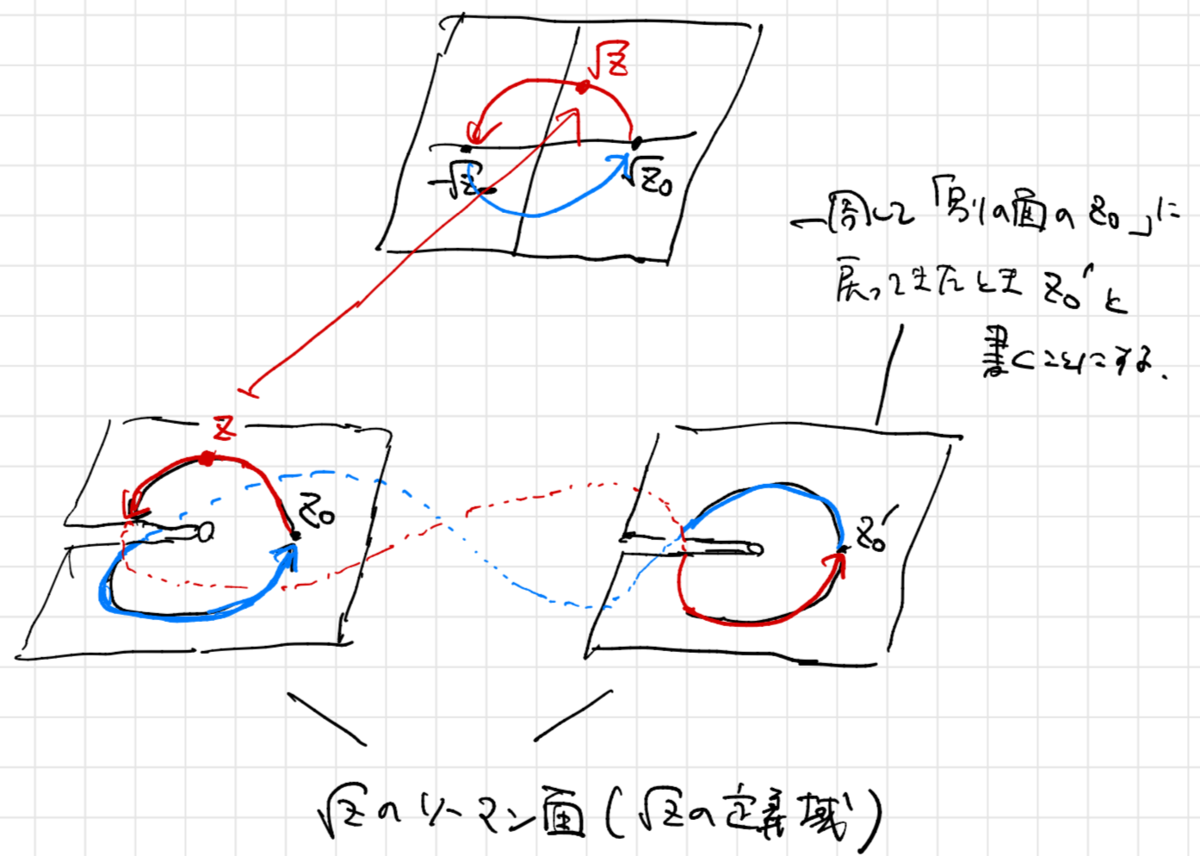
このようにすると、左側の面の からスタートして、左回りに移動し、負の実軸をまたぐ瞬間に、右側(2枚目)の面に移動します。また、ぐるっと回って右側の面の
に戻ってきます。2枚目の面の座標
に相当する点を
のように「ダッシュ記号」を使って表すことにしましょう。
における
の値は
となります。
に一致しません。しかしながら、この場合は同じ座標
であっても乗っている面が異なりますので、
だと思えます。よって、関数の値
が
と異なっていても問題ありません。
もう一度、右側の面で左回りに移動すると、今度は1枚目の面に戻ってきます。最終的に に戻ってくると、関数の値は
となるわけです。
すなわち、 という関数の定義域は、本質的に上記の2枚の複素数平面だった、というわけです。このように複数の複素数平面を貼り合わせてできる面のことを、一般に リーマン面 と言います。
関数 は、上記のリーマン面上の1価正則関数だった というわけですね。
4. 「√-2 × √-8 = √16?」の問題
さて、このような準備のもとで、元々の
の問題について考えてみましょう。
ここで考えたいのは、 とした部分の正当性です。実は、上記のリーマン面上の関数として見たときに
は一般に成り立ちます。ただし「リーマン面上のどの点であるか」をきちんと考えればの話です。
我々は日頃、 という計算をカジュアルに考えていますが、どこの面で成り立つのかということを真面目に考える必要があるということです。
を左の面の座標だと考えましょう。このとき、
の
は右の面の
という座標です。正確にいうならば、リーマン面の右側の座標であることを表す「ダッシュ記号」を用いて
と表すべきなのです。この は座標の値としては
と同じものを指していますが、リーマン面では相異なる点です。
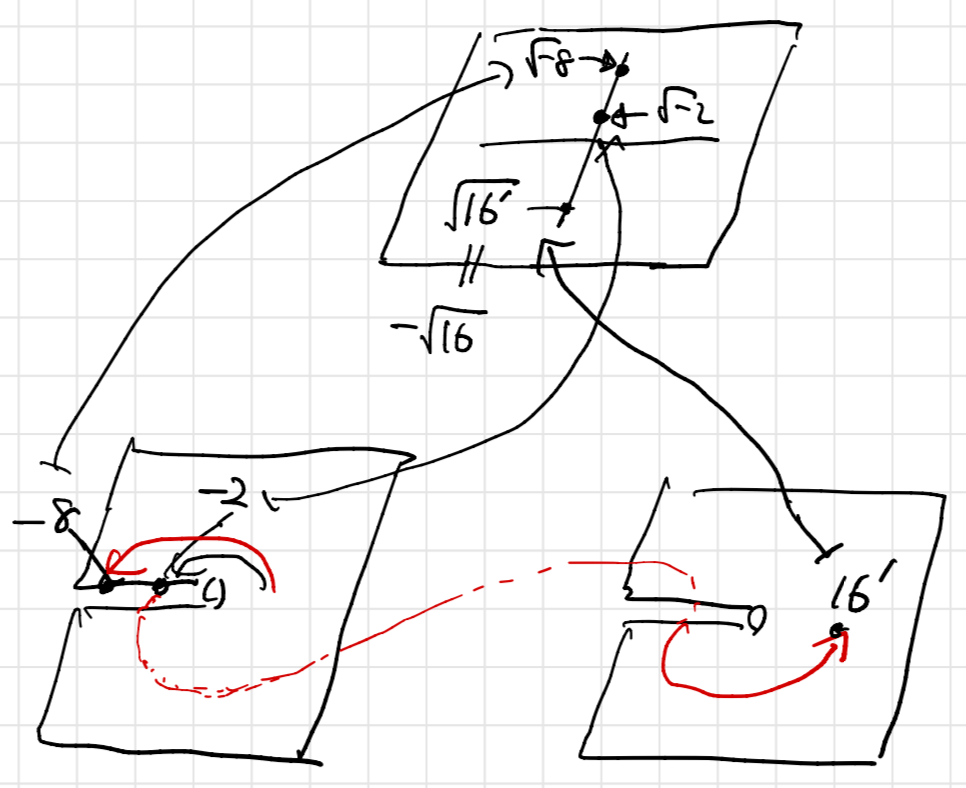
この場合、 における
の値は、左回りのモノドロミーの影響を考慮してマイナスがつきます。すなわち
となります。
したがって、
となり、ちゃんと正しい値が計算できています!!
これがこの問題のカラクリでした。
まとめると、複素関数の を考えるときは、適切にリーマン面を考える必要があるということですね。
いやー、とても楽しかったです。平方根って奥が深いですね!
元々の問題を提供してくれた @sakubunkake さんに感謝です!
それでは今日はこの辺で!
また、今回の内容は私が独自に考えたものなので、間違っているなどのご指摘がありましたら、こっそりTwitterのDM等で教えてください。
追記(2020/07/11 15:00):
記事の公開後に、上で書いた話を 複素数の偏角 によってスッキリまとめられることに気がつきました。
0ではない任意の複素数 に対して、
の偏角とは、
を実数
を用いて
と表したときの として定義されます。これを
と書くことにしましょう。
は、
を指すベクトルが実軸となす角という幾何的な意味を持ちます。だから偏 角 というわけですね。

もちろん、上の定義のままでは偏角は に対して一意に定まりません。
のように、2周、3周したときにも同じ値になってしまうからですね。
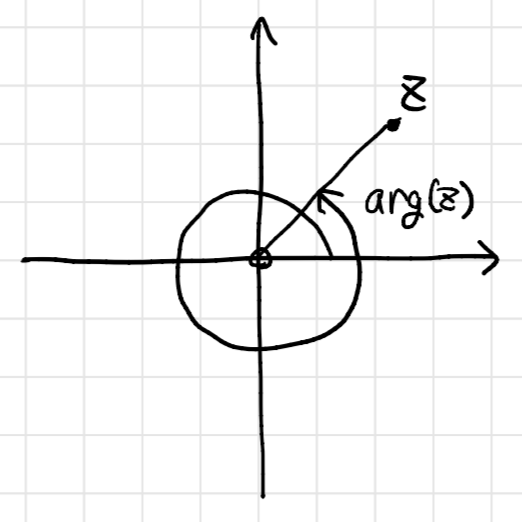
通常は、偏角はたとえば のように、範囲を限定してとります。
ここでは、上で議論したリーマン面を想定しつつ、 の範囲でとることにします。そして
の偏角が
のとき は左の面に、
のとき は右の面にあると考えます。
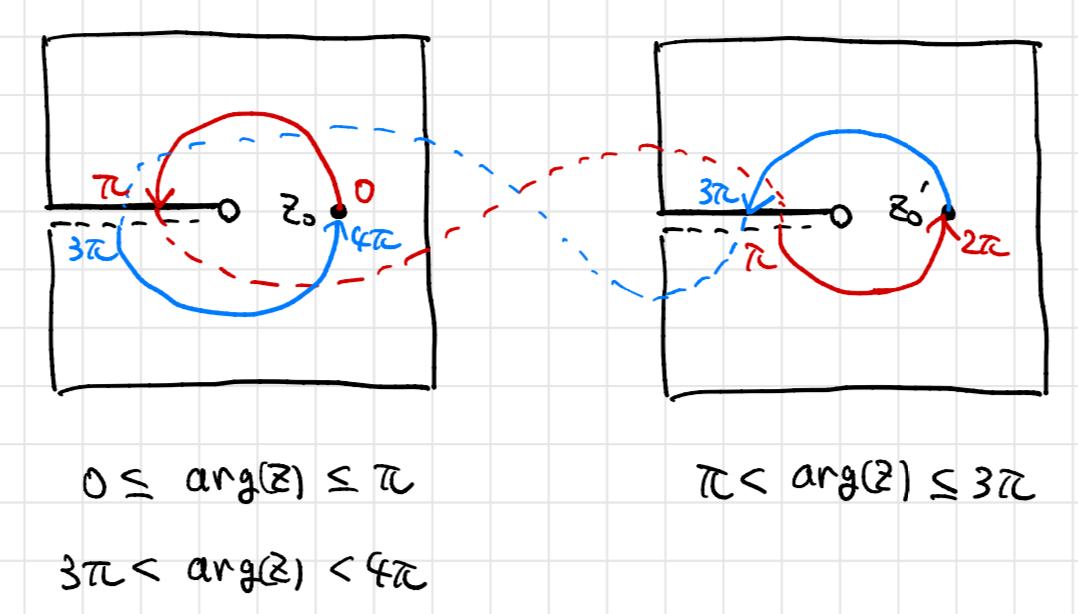
これで、偏角によって左と右の面を区別できるようになりました。
この状況で、リーマン面上の関数 を定義することができます。
としたとき
とします。
ここで、元々の問題に戻ると、 は
と表すことができますね。
次に、 を考えると、ド・モアブルの定理により
となります。偏角が なので、この数は右の面にいますね。これを
と書くことにしましょう。
通常の複素数で考えると と
は等しいわけですが、
のリーマン面上では
です。
さて、 を計算すると
となり、たしかに が成り立っていますね。
最後の計算で、
はてブでご指摘いただいた方、ありがとうございます!
具体的に計算できると納得感が増しますね。