先ほど、YouTubeでtsujimotterのプレゼン動画が公開されました! ぜひみなさまにご覧いただきたくて、ブログでも紹介したいと思います。
記事の後半では、私のこだわりポイントも紹介したいと思いますので、ぜひ最後まで読んでください。ちょっと趣向を凝らしています。
「tsujimotterのYouTubeチャンネル」というところで公開しています。以前からこのYouTubeチャンネルは持っていたのですが、あまり力を入れていませんでした。これを機に本格的に稼働させていこうと思っていますので、チャンネル登録よろしくお願いします!
どんな内容の動画?
2020年5月30日に ロマンティック数学ナイト というイベントがオンラインで開催されました。tsujimotterはその中で496秒の時間をもらって発表させていただきました。タイトルは 『「にじたい」へのいざない』 です。
私が最近精力的に勉強している 2次体 について、その面白さを紹介する内容になっています。
2次体というのは、本来少し専門的な内容なのですが、今回はその魅力をいかに伝えるかという点を工夫していますので、2次体なんて初めて知ったという方も楽しめる内容になっているのではないかと思います。
特に、2次体を考えるきっかけとして 「素数がめっちゃ出てくる多項式」 も紹介しています。
ぜひ一度ご覧になってください! 動画の感想もお待ちしています!!
(YouTubeのコメント欄かTwitter等にどうぞ)
プレゼンのこだわりポイント(インタビュー記事風)
せっかくなので発表に当たって考えていたことや、自分なりのプレゼンの工夫点・こだわりについて語ってみようかなと思います。こういうのってなかなか語る機会がないんですよね。今回は、特に色々と考えて作ったので、それをまとめることにも一定の価値があると思いました。
ちょっとした思いつきで、音楽雑誌のインタビュー記事風に書いてみました。
(アーティストがCDを出すときにインタビューされるイメージ)

写真・2次体の魅力について熱く語る日曜数学者tsujimotterこと辻順平さん
————プレゼン動画の公開おめでとうございます。まずは、辻さんの今回のプレゼンで「2次体」をテーマに選んだきっかけについて教えてください。
tsujimotter(以下、辻) ロマ数で発表させていただくにあたって、いつも考えていることは2つあります。一つはこれまでで最高の発表をしようということ。もう一つは今一番アツい話をしようということです。やっぱり僕の場合は、自分が心から面白いと思っていないと楽しく伝えることはできないんですよね。
実は4月くらいまでは、新型コロナの影響もあって数学に対するモチベーションがやや下がってしまっていました。
その中でずっとコンスタントに続けてきた活動が毎週水曜の「ゆるにじたい(「素数と2次体の整数論」の読書会)」だったのです。おかげさまで数学のモチベーションを保つことができて、2次体や関連する話題に関心が向いてきました。
そういうわけで、2次体をテーマにしてもいいのかなと思いながら発表の準備を進めていたら、これが楽しかったんですね。それで私のパートナーに2次体の話をしてみたんです。
実はこれまでも何度か2次体に関連する話をしたことはあったのですが、全然関心を持ってもらえなかったのです。でも、今回はとても響いて興味をもってもらえました。そこで、これはいけると思いましたね。笑
興味を持ってもらえるイントロ
————なるほど。2次体について伝えるのはなかなか難しいと思うのですが、辻さんのプレゼンではどのような点を工夫されたのでしょうか。
辻 今回特に工夫したところは、導入の部分です。一般向けの本で2次体を紹介するときは決まって「素数 が
で表される条件(2平方和の定理)」から始まります。
もちろん、この例自体はとても面白くて、フェルマー・オイラー・ガウスら、数論の土台を作ってきた大数学者らが、この定理をきっかけに数論を発展させてきたという背景があるわけです。かくいう私もこの定理に興味をもって、数論の世界にいざなわれました。
しかしながら、私自身がこれまで何度かこの問題を紹介して感じたのは、この2平方和の定理は万人に興味をもってもらえるようなものではなさそうだということです。
————人を選ぶということでしょうか。
辻 はい、そうなんです。2平方和の定理はある程度数論の世界の前提を知っている人には面白く感じられるでしょうし、奥も深いので、一度ハマるとどっぷりと沼に引きずり込まれるような問題です。
しかし、逆にそうではない人にとっては「なぜ素数を平方数の和に表したいのかわからない」という問題があります。そこで突っかかってしまうと、いかに面白おかしく「説明」したところで、相手の心には響かない。
そのように考えているうちに、私自身が2次体の話に強く興味を持ったもう一つのきっかけを思い出しました。それが「素数生成多項式」です。素数がたくさん出てくる魔法の多項式、素数さえ知っていれば、面白く感じるための障壁はありません。
しかも、その素朴な事実の背景に、2次体の整数環における「素因数分解の一意性」が関わってくるのです。これは面白い。
そんなわけで、素数生成多項式をイントロに据えた2次体の整数論の導入プレゼンを構成することにしました。

2次体の「魅力」は何なのか
————それは面白そうですね。イントロの内容が決まってからは、プレゼンの準備はスムーズにいったのでしょうか。
辻 そうですね。イントロの内容を決めてからは、かなりスムーズに進んでいきました。ただ一点、「2次体を考えることの面白さ」の伝え方については、だいぶ悩みました。
2次体の整数環の素因数分解の一意性を考えることで、素数生成多項式の条件が明らかになるというのは数学的な事実です。しかし、それを説明したところで、2次体を考えることの何が一体面白いのかは伝わりません。結局、証明に必要だから2次体が導入されたんですね、という程度で理解されてしまったら面白くない。
私が感じている2次体の面白さは何であるかを明らかにして、それを具体的なメッセージとして伝える必要がありました。
説明にあたっては、ある程度細かい話はばっさりカットしました。「整数環」という用語の説明とか、「単数」の扱いとか、「素因数分解の一意性」の正確な意味とか。「イデアル」とか「類数」とか。この辺は2次体の理論においては重要なトピックだけれども、今回の話の本題ではない。
これらの用語は簡単に説明できるとは思わないし、説明したところでそれは僕が伝えたい魅力を伝えることには繋がらないからです。私は2次体の「説明」をしたいのではなく「魅力」を伝えたいのだから。
————なるほど。辻さんの発表では「数の世界を広げる」という言葉が出てきましたが、その辺りが2次体の魅力を表すキーワードになるのでしょうか。
辻 そうとも言えるし、そうではないとも言えます。2次体のような「有理数体より大きな代数体」の導入をするとき、しばしば「数の世界を広げる」という表現がなされます。しかしその言い回しで本当に十分かどうか疑問に思っていました。
数の世界を広げるのであれば、高校生でも知っている実数や複素数の集合があるわけです。これじゃあダメなのか。を加えるんだったら、複素数だっていいじゃないか。なんで中途半端な
みたいな集合を考えるのか。
————実際、その中途半端さ具合もあまり伝わっていなかったりしますよね。「あぁ、複素数を考えているんですね」みたいな理解のされ方をしてしまって。
辻 そうなんですよ。そこで、僕がとった紹介の仕方はこうです。
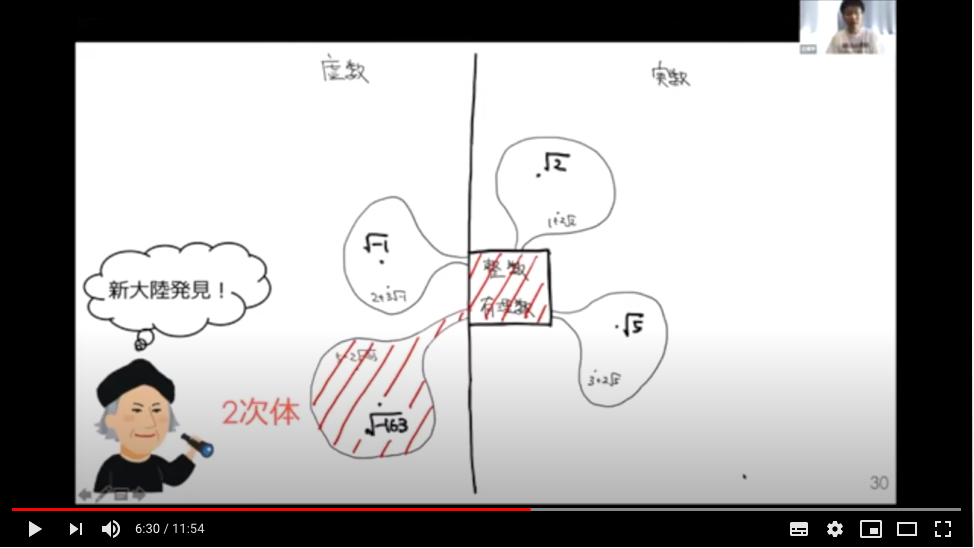
「数の世界を広げるんだけど、実数や複素数のような大きすぎる集合ではなく、整数論が展開できるギリギリまで数の世界を広げる、その考え方が面白いんだ」と。
この考え方は2次体の世界を知らない人にとっては、なかなか斬新な考え方だと思うし、あまり語られない部分だと思っています。整数論を知っている人はみんな当たり前に思っているのかもしれませんが。
そのことを図示するような集合の描き方も開発しました。これについては分かりやすいというコメントをたくさんいただきました。
数を好きになってもらいたい
————プレゼンで他に工夫されたところはありますでしょうか? 冒頭の素数生成多項式の紹介では、図を使って説明していたと思いますが。
辻 そうですね。冒頭はいわゆる「掴み」の部分なので、問題意識を共有して、問題そのものに興味をもってもらえるよう工夫しました。
特に、一般の「オイラーの幸運数」(プレゼン中は「ティック数」と表現)であるような は実はレアであって、
が魅力的なんだということを知ってもらいたい。そのために、多項式が生成する数が素数かどうかを 可視化できるページ を作ったというのが大きな工夫点です。
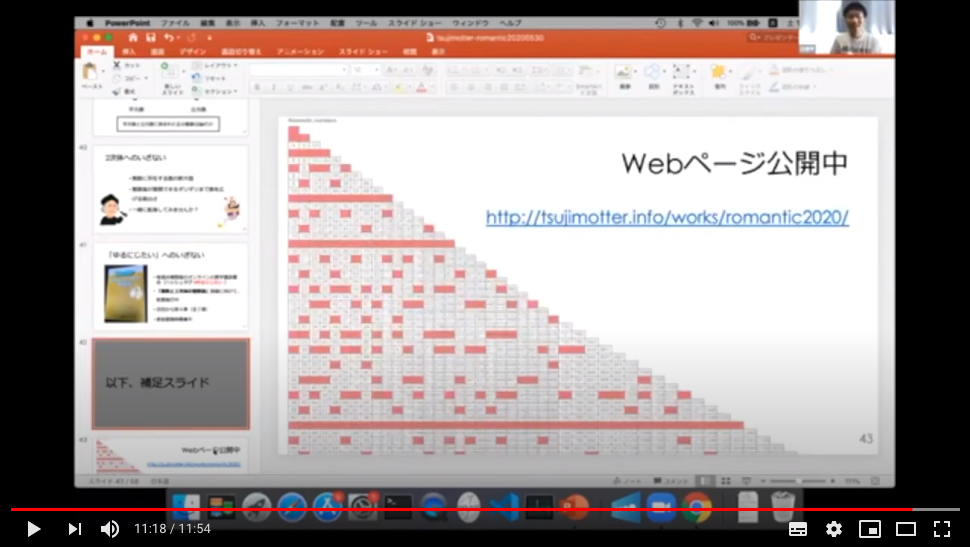
41が素数生成多項式であることはよく語られるけど、それが最後であることはあまりうまく説明されない。伝わっていないことが多い。
もちろん、この辺の話は有名な事実で、調べれば簡単にわかるし、tsujimotterのノートブック にも載っています。しかし、知らない人は多いです。ロマ数のような講演で、そのような前提知識を聞き手の知識に委ねてしまうのはどうかなと思っています。
————最後に が出てきたところでは、Twitterのコメントでも歓声が起きていましたね。
辻 そうなんです! 今回のプレゼンでは最初の方で「 という数を覚えておいてください」と言っています。その後一般論を展開してから、最後にまた
が出てくるという構成にしました。
今回のプレゼンでは、Twitterの反応はとても多かったのですが、特にそのコメントは嬉しかったですね。狙い通りにうまくいったぜという感じです。
スライドの枚数を にしたのも、密かなこだわりでした。自分で言ってしまいましたが。笑
今回のプレゼンを通して、 や
という数を好きになってもらえたらと思っています。
アウトプットを通した学び
辻 今回、素数生成多項式の話をするので、改めて昔の記事を読み返してみたんですね。「なかなかよく書けているな」と自分で思ったのですが。笑
ただ、証明にちょっと不備があることがわかってしまいました。近々それを修正するような記事を書きたいと思っています。
また、証明を見直したことによって新たに気づいたこともあり、今ここでは述べられないのですが、近いうちに何かしらの方法で紹介したいと思っています。
————発表をきっかけに学びがあったと言うことですね。
辻 そうです。発表をすることによって、たとえ今までよく知っていると思っていたことでも、改めて精緻に見直すことになります。そこで思いもよらない発見があったりします。
こういうことがあるので、発表はやめられないですね。以前、佐野さんのインターネットラジオ でお邪魔したときにも語ったのですが、アウトプットを通した学びの有用性を日々実感しています。
ファンの方へのメッセージ
————最後にファンの方に向けたメッセージをお願いします。
辻 発表の動画やこの記事を見ていただいてありがとうございます。今回の発表を通して、私のお気に入りの対象である、2次体や素数生成多項式に興味を持ってもらえたら嬉しいです。こうした対象は少し難しいので、なかなか手を出しにくかったかと思いますが、ぜひ私の発表をきっかけに手を伸ばしてみてもらえたらと思います。
また、Twitterでのコメントがいつも励みになっています。面白いなと思った部分や「おおっ!」と思ったこと、その他感想など、TwitterやYouTubeのコメント欄でコメントいただけると嬉しいです。
最後になりましたが、今回、発表者として選んでいただきましたロマンティック数学ナイトの運営のみなさま、和から株式会社のみなさま、楽しく司会進行してくださったタカタ先生、その他応援してくださったみなさまに感謝申し上げます。ありがとうございます。
これからも私の日曜数学の様子を楽しく発信できたらと思っていますので、引き続き応援よろしくお願いします!
————tsujimotterさん、どうもありがとうございました!
