無理数の無理数乗は無理数か？

この記事は明日話したくなる数学豆知識アドベントカレンダーの 7日目の記事です。（６日目：ほとんどいたるところ）

無理数とは、有理数でない数のことです。

有理数とは $\displaystyle \frac{2}{3}, \frac{100}{9}$ のように分数（分母がゼロでない整数の比）で表せる数のことですね。
分母が　 $1$ になってもいいので、 $2$ や $-3$ のような整数も有理数です。

無理数の例としては、 $\sqrt{2}$ だとか $\pi$ だとか $e$ だとかがあるかと思います。
もちろんほかにもうんざりするほどありますよ。
なんたって、数直線上を適当に指したときに、その指の先が示す数は、ほぼ間違いなく無理数です（図１）。無理数のほうが有理数よりはるかに多いのです。

f:id:tsujimotter:20141203185622p:plain:w400

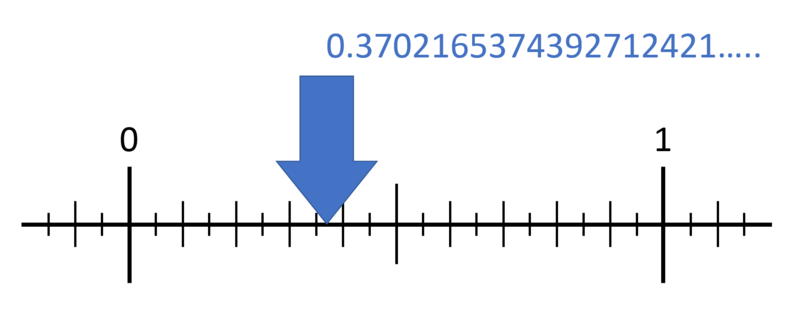
図１：「数直線上のほとんどの点は無理数」のイメージ

さて、この無理数という数は非常に厄介な数です。
無理数の条件というのは、基本的には「有理数ではない」ということだけなので「すべての無理数がどんな数であるか」という問いに対しては、あまり気の利いた答えを返すことが出来ません。よくわからないのです。

これは「すべての宇宙人」を考えるようなもので、金星人も土星人もいますし、特定の星に定住しないような人もいるかもしれませんが、これらすべて「宇宙人」すなわち「すべての地球人でない人」に含まれますね。すべての宇宙人に共通するような性質っていったいなんでしょう。

この宇宙人の例えのように、非常に扱いづらい無理数ですが、せめてその姿の一端を垣間みることは出来ないのでしょうか。すなわち、すべての無理数に適用できるような面白い数学の定理はないのでしょうか。

たとえば、無理数の無理数乗はすべて無理数だったり、しないでしょうか。具体的に $\displaystyle \sqrt{2}^\pi, \pi^e$ などを考えてみると、なんとなく正しいような気もしてきます。直感的には、すべての無理数の無理数乗は無理数になりそうです。

淡い期待を打ち砕く残念なお知らせですが、すべての無理数の無理数乗が無理数になるわけではありません。すなわち、無理数の無理数乗であらわされる有理数が存在します。

今からそんな興味深い例をご紹介しましょう。

次の数を考えます。

f:id:tsujimotter:20141203191134p:plain:w160

$\sqrt{2}$ は無理数ですから、この数もたしかに「無理数の無理数乗」ですね。

この数を使って、以下を証明しましょう。

（定理）
無理数の無理数乗で表される有理数が少なくとも１つ存在する

$\sqrt{2}^\sqrt{2}$ をうまく使って、「無理数の無理数乗が有理数」となる実例を１つ示すことにします。

この問題に対するうまいアイデアは、場合分けを使うことです。 $\displaystyle \sqrt{2}^\sqrt{2}$ が有理数であるか無理数であるかの 2 通りで考えてみましょう。

（証明）
1. $\displaystyle \sqrt{2}^\sqrt{2}$ が有理数であると仮定する
$\sqrt{2}$ は無理数。仮定より $\displaystyle \sqrt{2}^\sqrt{2}$ は有理数。したがって $\displaystyle \sqrt{2}^\sqrt{2}$ は、無理数の無理数乗であらわされる有理数である。

2. $\displaystyle \sqrt{2}^\sqrt{2}$ が無理数であると仮定する
仮定より $\displaystyle \sqrt{2}^\sqrt{2}$ は無理数。これの√2乗をとると、この数は無理数の無理数乗である。
$\displaystyle \left(\sqrt{2}^\sqrt{2}\right)^\sqrt{2}$
さて、これを計算していくと、
$\displaystyle \left(\sqrt{2}^\sqrt{2}\right)^\sqrt{2} = \sqrt{2}^{\sqrt{2}\times\sqrt{2}} = \sqrt{2}^{2} = 2$
よって、 $2$ すなわち有理数が得られた。したがって $\displaystyle \left(\sqrt{2}^\sqrt{2}\right)^\sqrt{2}$ は、無理数の無理数乗であらわされる有理数である。

以上 1. 2. のいずれの場合においても、「無理数の無理数乗で表される有理数が少なくとも１つ存在する」ことを示すことができた。
（証明終わり）

いかがだったでしょうか。
わからなかった方のために図で示してみましょう。

f:id:tsujimotter:20141203191058p:plain:w400

図２：無理数の無理数乗で表される有理数が少なくとも１つ存在する

たしかに、いずれの場合においても、「無理数の無理数乗で表される有理数が少なくとも１つ存在する」ことがわかりますね。

この証明の面白いところは「 $\displaystyle \sqrt{2}^\sqrt{2}$ が無理数か有理数かどうか」は一切わからないにもかかわらず、元の命題を証明できてしまうところです。なんとも不思議ですね！

実は、この $\displaystyle \sqrt{2}^\sqrt{2}$ という数は、無理数であることが知られています。しかも無理数の中の無理数、超越数です。（「超越数とは何か」が分からない人は、End01nojo 氏のこの記事を参照。）
この証明は簡単ではありませんが、「ゲルフォント＝シュナイダーの定理」を知っていればその系として示すことができます。（「ゲルフォント＝シュナイダー」の定理は、超越数を判定するための奥義みたいな定理です。超越数であれば無理数なので、無理数かどうか判定できます。）