多項式関数に接する多項式関数（2021年共通テスト数学ⅡB・第2問）

2021年から「センター試験」が「大学入学共通テスト」という名前に代わり、傾向も以前とは変わったということで各所で話題になりましたね。受験生の皆様はお疲れ様でした。

tsujimotterは例年、数学だけは自分で解くようにしているのですが、今年も数学Ⅰ・数学Ａと数学Ⅱ・数学Ｂについて時間制限付きで解いてみました。現役から離れて十数年たっているので、大学合格は難しそうな結果に終わってしまったのですが、いろいろ面白い問題があって解いてみてよかったなと思います。

色々紹介したい問題はたくさんあったのですが、今回考えたいのは数学Ⅱ・数学Ｂの第２問です。これについては高校数学の範囲を超えて、色々掘り下げられそうな気がしました。

問題をそのまま掲載するのは気が引けますので、各自検索して確認してください。たとえばこちらのページでは、問題と回答が載っています。まだ解いていない人は自分で考えてみると面白いかもしれません。
edu.chunichi.co.jp

諸注意：
本ブログ記事では共通テストの問題を扱っていますが、日曜数学者 tsujimotter が趣味で勉強した内容を発表するブログ記事であり、受験生向けの解説記事ではありません。

「センター試験の問題を大学以降の数学を使って色々考察してみた」という内容になっていますので、受験に役に立つテクニックといった類のものではないことをあらかじめお伝えしておきます。内容に興味がある受験生の方は「受験の息抜きに」ぐらいの気持ちで読んでいただければと思います。

目次：

1. 関連する日曜数学会の発表

2. 2次関数の x = 0 における接線

3. n次多項式に一般化しよう

4. 二重数環

5. ザリスキー接空間

6. おわりに

おまけ

続きを書きました！

1. 関連する日曜数学会の発表

実は、今回の記事の前半部分の内容については、1月で行われた日曜数学会というイベントにて、Shimoya-manさんという方によって発表されています。タイトルは「接線を微分を使わず求めたい」というもので、まさにこんな内容ですね。近々発表の様子が動画で公開されるかと思いますので、そのときにこちらに共有いたします。

動画が公開されたので共有します！

2. 2次関数の x = 0 における接線

今回、考えたい第２問は「2次関数の接線」を扱う問題でした。

一般に

$y = f(x) = ax^2 + bx + c \tag{1}$

の形で表される2次関数を考えたときに、 $x = 0$ で $y = f(x)$ に接する接線の方程式を求めよ、という問題を考えてみましょう。

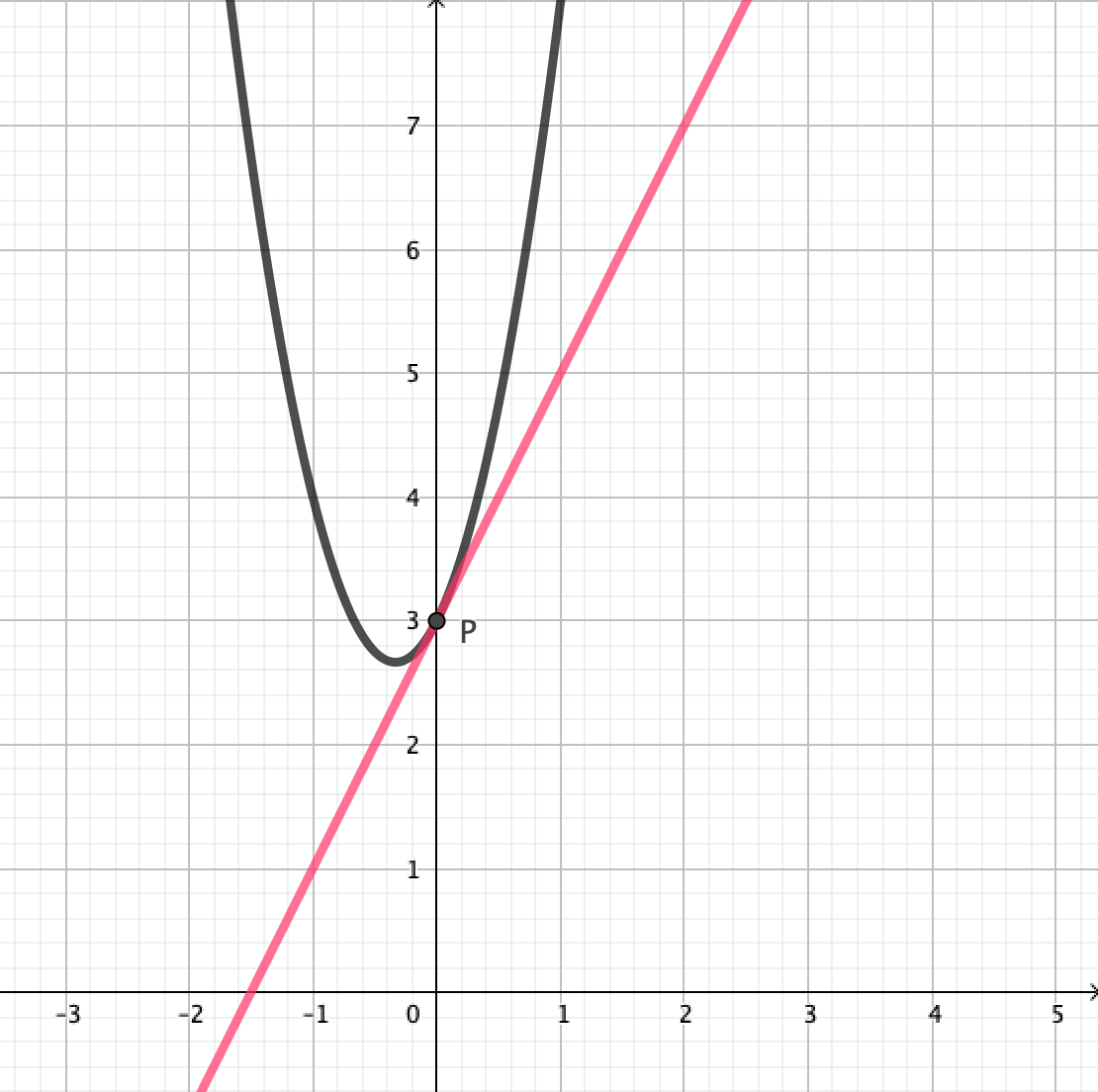
実はこの問題、一瞬で解けるのですが、素朴に考えてみましょう。接線の傾きは $f(x)$ の微分 $f'(x) = 2ax + b$ に、 $x = 0$ を代入して得られるので $f'(0) = b$ です。また、接線の $y$ 切片は $f(0) = c$ となるので、接線の方程式は

$y = g(x) = bx + c \tag{2}$

と表せますね。これでできあがりです。

さて、ここで式 $(1)$ と式 $(2)$ を見比べてみると、実は 1次の項と0次の項がまったく同じですね！なので、係数をみるだけで一瞬で解けるわけです。

実際、微分の過程をみると微分 $f'(x) = 2ax + b$ を求める際に1次の係数 $b$ が定数項になり、 $x = 0$ にすることで定数項だけが残ります。これが接線の1次の係数になるので、また1次に戻ってくるわけですね。 $c$ の方も、元々 $f(x) = ax^2 + bx + c$ の定数項で、 $x = 0$ とすることでやはり1次以上の項が消えて、接線の方程式の定数項に戻ってくるわけです。接線の方程式が $f(x)$ の1次以下を見れば良いというのは、そりゃそうだという感じがしますね。

もう少し見方を変えてみましょう。先ほどは、 $y = f(x)$ に接する接線 $y = g(x)$ を考えたわけですが、今度は $f(x) - g(x)$ を考えてみましょう。 $f(x)$ と $g(x)$ が $x = 0$ で接するので、 $f(x) - g(x)$ の方は $x$ 軸と接することになりますよね。

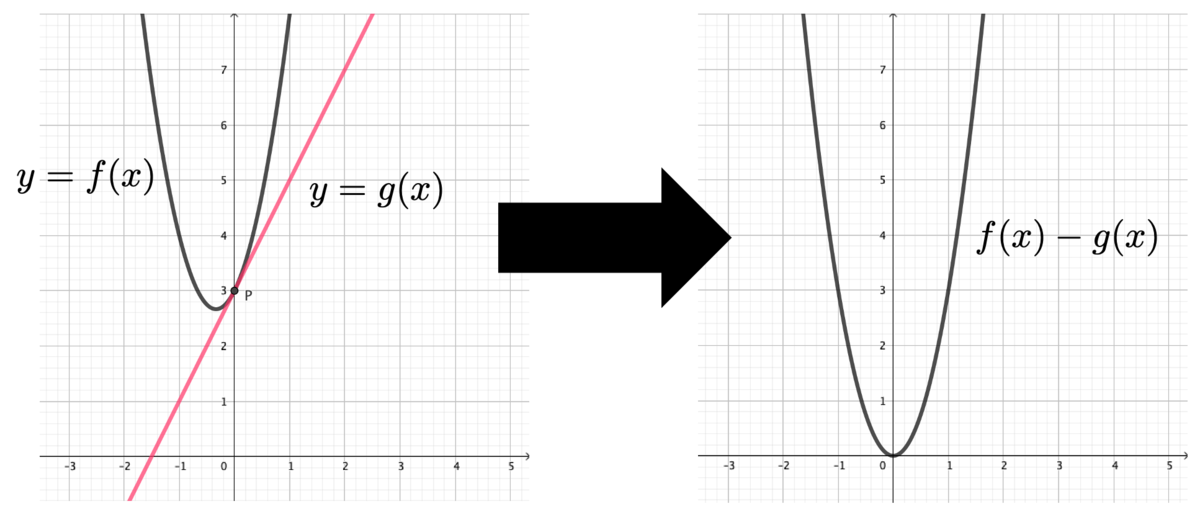
$f(x) - g(x)$ が $x = 0$ で $x$ 軸に接するということは、 $x = 0$ で重根を持つということです。 $f(x), g(x)$ は高々2次多項式なので、 $f(x) - g(x)$ も2次多項式であることに着目すると

$f(x) - g(x) = Ax^2$ （ $A$ はある定数）

が成り立つということがわかりますね。今、 $f(x)$ の2次の係数が $a$ であって、 $g(x)$ は1次であることを仮定していますので、 $A = a$ となります。

よって

$g(x) = f(x) - ax^2 = bx + c$

となり、 $g(x) = bx + c$ であることの説明ができましたね。

ここからの教訓で、一般に $x = p$ における接線を同様の方法で求めることもできそうですね。 $f(x) - g(x)$ が $x = p$ で重根を持つということなので、同様のロジックで

$f(x) - g(x) = A(x - p)^2$

と表せることになりますね。

接線を手早く求めたいときにぜひ使ってみてください。

3. n次多項式に一般化しよう

ここまでは十分高校数学の範囲だと思いますが、この辺からだんだんと逸脱していきます。

上の話は、 $f(x)$ を2次多項式、 $g(x)$ を1次多項式として、 $y = f(x)$ と $y = g(x)$ が $x = 0$ （あるいは一般に $x = p$ ）で接する問題について考えました。

これは一般の次数の多項式にしても、同じように議論できそうですね。つまり、 $f(x), g(x)$ を高々 $n$ 次の多項式としたときに、 $y = f(x), y = g(x)$ が $x = p$ で接する状況を考えましょう。

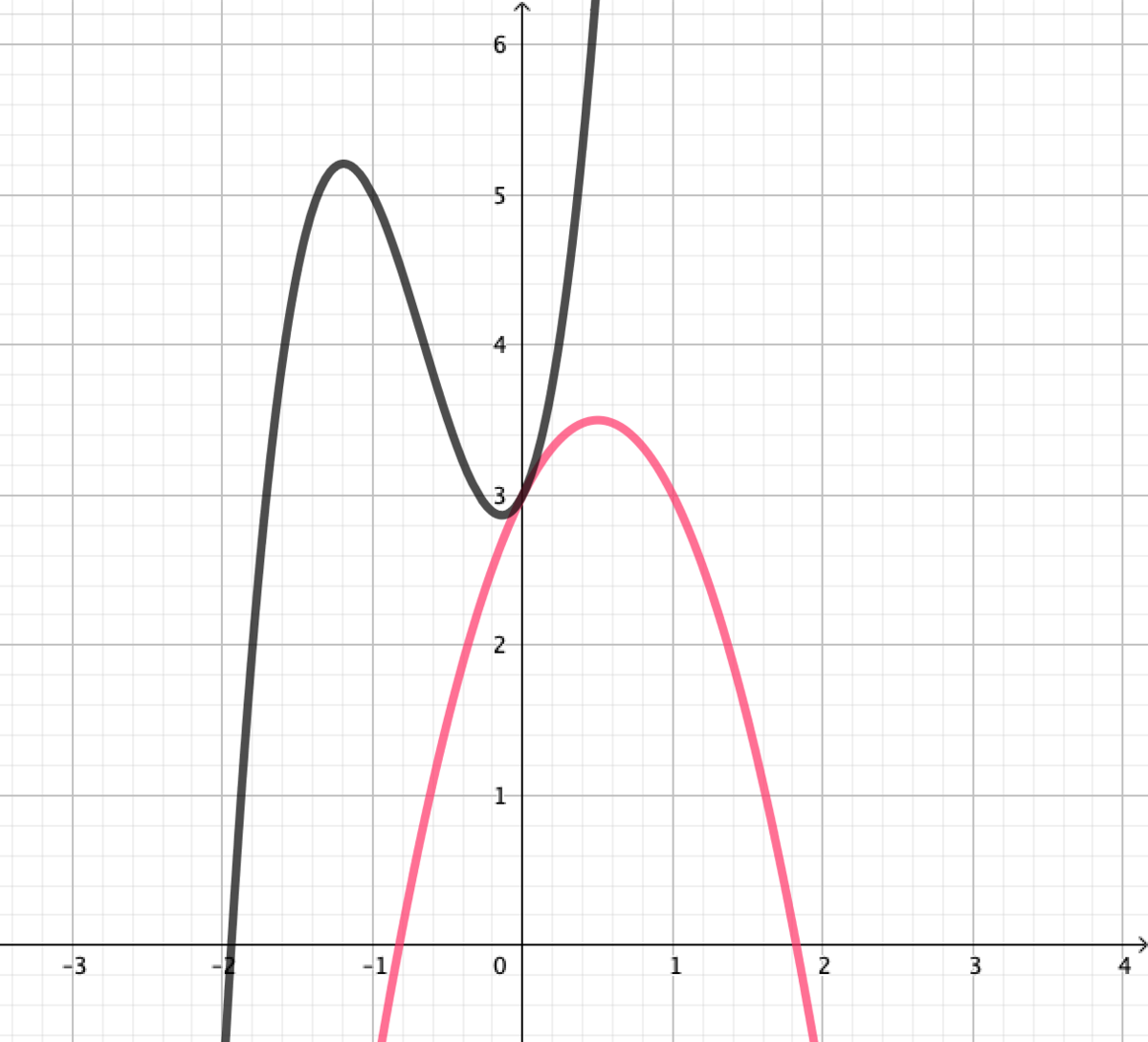
これも結局 $f(x) - g(x)$ が $x = p$ で重根を持つという条件を考えればよいわけです。したがって

$f(x) - g(x) = (x-p)^2 h(x)$ （ただし、 $h(x)$ は高々 $n-2$ 次の多項式）

と表せるわけですね。これが成り立つとき $f(x), g(x)$ は $x = p$ で接するというわけです。

少しだけ言い換えると

$f(x) - g(x)$ は $(x-p)^2$ で割り切れる

ということもできそうですね。この条件は次の節で使いますので、覚えておいてください。

この重根を持つという条件、実はいろんな言い方で言い換えることができて、たとえば

多項式 $f - g$ の判別式 $\Delta(f-g)$ が $0$
$f(x) - g(x)$ とその微分 $f'(x) - g'(x)$ が共通根を持つ
終結式 $\operatorname{Res}(f-g, f'-g')$ が $0$

などということもできそうです。

詳しくは龍孫江さんの動画が参考になります。
www.youtube.com

4. 二重数環

前節において、多項式が点 $p$ で接する条件を、「多項式を $(x-p)^2$ で割り切れる」という言葉を用いて言い換えることができました。

$f(x)$ と $g(x)$ は $x = p$ で接する $\;\; \Longleftrightarrow \;\;$ $f(x) - g(x)$ は $(x-p)^2$ で割り切れる

そこで、多項式環の言葉を使って問題を整理できないでしょうか？

実際、多項式環 $\mathbb{R}[x]$ の元 $f, g$ に対して

$f \sim g$ $\;\; \Longleftrightarrow \;\;$ $f(x) - g(x)$ は $(x-p)^2$ で割り切れる

という同値関係を入れたくなると思います。

そこで

$R = \mathbb{R}[x] / ((x-p)^2)$

という剰余環を考えたくなるのは自然かと思います。

剰余環 $R$ の任意の元（剰余類） $[f]$ は、

$[f] \; = \; f + (x-p)^2 \mathbb{R}[x]$

と表せます。

この剰余類は、代表元 $f(x)$ に $(x-p)^2 g(x)$ という形の多項式を加えて得られる多項式全体を表します。言い換えると「 $f(x)$ に $x = p$ で接する多項式全体」ということになります。

（図は $y = 4x^3 + 8x^2 + 2x + 3$ に $x = 0$ で接する多項式関数の例）

ここで、多項式 $f(x) \in \mathbb{R}[x]$ を $(x-p)^2$ で割ったあまりを取れば、

$f(x) = ax + b + (x-p)^2 g(x)$

となり、 $ax+b$ のように1次多項式で表せます。これは、 $R = \mathbb{R}[x] / ((x-p)^2)$ の任意の剰余類は、1次多項式によって代表されることを意味しています。

言い換えると、 $R = \mathbb{R}[x] / ((x-p)^2)$ の任意の剰余類は

「1次関数（直線） $y = ax + b$ に $x = p$ で接する多項式全体」

だったというわけです。 $R$ はこのような剰余類全体なので、「1次関数全体」と同一視できるわけですね。

さらに、環 $R = \mathbb{R}[x] / ((x-p)^2)$ の構造を考えてみましょう。

$\varepsilon$ を $\varepsilon^2 = 0$ となるような数としたとき、

$\begin{align*} \phi \colon \;\;\mathbb{R}[x] \;\;\; &\longrightarrow \; \mathbb{R}[\varepsilon], \\ a + b(x-p) + g(x) (x-p)^2 &\longmapsto a + b\varepsilon \end{align*}$

なる環準同型写像 $\phi$ を考えてみましょう。要するに、 $(x-p)^2$ を $0$ にして $(x-p)$ を $\varepsilon$ に置き換える環準同型ですね。これは全射であり、 $\operatorname{ker}\phi = ( (x-p)^2 )$ なので、準同型定理より

$\begin{align*} \phi \colon \mathbb{R}[x] / ((x-p)^2) &\;\; \simeq \; \; \mathbb{R}[\varepsilon], \\ [a + b(x-p)] &\longmapsto a + b\varepsilon \end{align*}$

なる環の同型が得られます。

右辺の $\mathbb{R}[\varepsilon ]$ は二重数環と呼ばれるものです。 $\mathbb{R}[\varepsilon ]$ の任意の元を二重数といいます。複素数みたいな $\mathbb{R}$ 上の2次元ベクトル空間ですが、複素数と異なり $\varepsilon^2 = 0$ となるような構造が入っています。

二重数は $\varepsilon^2 = 0$ より整域ではないので、通常の数とは性質が異なりますが、便利に使える場面もあります。実際、二重数はよく「微分」を表現するのに使ったりしますね。 $\varepsilon = dx$ とすると、 $dx$ は2乗すると消えてしまうので、そのような状況を表すのにちょうどよい代数的な構造をしているわけです。

ところで、上の同型の元になった環準同型

$\begin{align*} \phi \colon \;\;\mathbb{R}[x] \;\;\; &\longrightarrow \; \mathbb{R}[\varepsilon], \\ a + b(x-p) + g(x) (x-p)^2 &\longmapsto a + b\varepsilon \end{align*}$

ですが、この環準同型は $f(x) = a + b(x-p) + g(x) (x-p)^2$ を「 $x - p$ の周りで1次関数に近似している」と見ることができます。これって、よくよく考えると微分そのものですね。

$\phi$ は「多項式を微分する環準同型」といっても良さそうです。

5. ザリスキー接空間

こんなことを考えているうちに、せっかく可換環論の話が出てきたので、代数幾何的な見方ができないかと思いました。もう少しだけ深掘りしてみましょう。

tsujimotterがちょうど2重数ぐらいまで考えているときに、第二宇宙賢者さんという方からヒント的なコメントをいただきまして、以下に述べるような方向性で考えてみようと思いました。

元々「ザリスキー接空間」自体知らない概念だったので、昨日定義を調べた上で、「多分こういうことなんじゃないか」と思いながら記事を書いています。なので、内容の正しさは全く保証できませんのでご了承ください。

まず、いま考えているのは $\mathbb{R}$ 上の多項式環 $\mathbb{R}[x]$ なわけです。代数幾何的にいうと、座標環が $\mathbb{R}[x]$ であって、対応するアフィンスキームが $X = \operatorname{Spec}\mathbb{R}[x]$ みたいな感じでしょうか。

$\mathbb{R}$ は代数閉体ではないので、あとあと不具合が起きないことを防ぐために、 $\mathbb{R}$ の代わりに $\mathbb{C}$ を考えた方がよいのかもしれません。（この辺の議論は確認せず、結構適当にやっていますので、ご容赦ください）

なお、アフィンスキームについては、昔こんな記事を書いたことがありました。参考までに。
tsujimotter.hatenablog.com

要するに、空間として数直線を考えていて、その上のたとえば $x = p$ の点が環 $\mathbb{R}[x]$ の素（極大）イデアル $P = (x-p)$ と同一視できるわけですね。

点 $P = (x-p)$ の周りで定義される正則関数（「極」を持たない関数）を考えましょう。たとえば、すべての多項式 $f \in \mathbb{R}[x]$ は極を持たないので正則ですね。ほかにも、有理関数 $f/g \in \mathbb{R}(x)$ を考えたときには、もし $g$ が $x - p$ に零点を持たないのであれば $f/g$ は点 $p$ の周りで正則です。言い換えると、 $g \not\in P = (x-p)$ であれば $f/g$ は点 $P$ の周りで正則な関数となります。

そのような状況を表すことができるのが環の局所化という概念で、素イデアル $P = (x - p)$ による $R$ の局所化

$R_{P} = \left\{ \cfrac{f}{g} \; \middle| \;\; f, g \in R, \;\; g \not\in P \right\}$

です。これは要するに、 $P = (x-p)$ の周りで正則な（極を持たない）有理関数全体を表す環です。

$R_{P}$ は局所環なので、唯一の極大イデアルを持つことになるのですが、それを $\mathfrak{m}_{P}$ と置くことにしましょう。これは

$\mathfrak{m}_{P} = (x-p) R_{P}$

というイデアルですが、要するに $x = p$ に零点を持つ有理関数全体ですね。

抽象的に定義されるので、一見では何のことかわからなくなりそうな対象たちですが、中身をきちんと考えればそこまで怖いものではありません。

また、 $R_P$ を極大イデアル $\mathfrak{m}_P$ で割った環 $k_P = R_P / \mathfrak{m}_P$ は、体になります。 $k_P$ を $P$ における剰余体といいます。剰余体では $(x-p)g(x)$ を $0$ と同一視するので、1次以上の項が全て消えて定数になってしまいます。よって、実質的には $k_P \simeq \mathbb{R}$ となりますね。

さて、この $\mathfrak{m}_P$ を $\mathfrak{m}_P^2$ で割って得られる商 $\mathfrak{m}_P / \mathfrak{m}_P^2$ を（ザリスキー）余接空間と呼ぶことにしましょう。ここから先は、これを理解することを目指したいと思います。

まず、 $\mathfrak{m}_P / \mathfrak{m}_P^2$ は、 $\mathfrak{m}_P$ を $\mathfrak{m}_P^2$ で割った商空間で、特に $k_P \simeq \mathbb{R}$ 上のベクトル空間になります。

$\mathfrak{m}_P$ はイデアルなので加法で閉じています。また、 $\mathfrak{m}_P$ の元 $(x-p)g(x)$ に剰余体 $k_P \simeq \mathbb{R}$ の元 $k$ をかけても $\mathfrak{m}_P$ の元になりますので、これは $k_P$ 上のベクトル空間になりますね。

$\mathfrak{m}_P^2$ は単項イデアル $(x-p)R_{P}$ の2乗なので、単に $(x-p)^2 R_P$ です。これは $\mathfrak{m}_P$ の部分空間になっています。したがって、 $\mathfrak{m}_P / \mathfrak{m}_P^2$ は、 $\mathfrak{m}_P$ を $\mathfrak{m}_P^2$ で割った商空間で、特に $k_P \simeq \mathbb{R}$ 上のベクトル空間になります。

$\mathfrak{m}_P / \mathfrak{m}_P^2$ は「 $x=p$ を零点に持つ有理関数全体の空間」を「 $(x-p)^2$ で割れる有理関数全体の空間」で割っているわけですが、これは2重数のときと同じような状況ですね。

つまり、ベクトル空間 $\mathfrak{m}_P / \mathfrak{m}_P^2$ の各点は「関数 $(x-p)g(x)$ （ $g(x)$ は点 $P$ で正則）に点 $P$ で接する有理関数全体」を表す剰余類ということになるわけです。また、 $g$ を

$g(x) = a + b(x-p) + c(x)(x-p)^2$
（ $a, b \in \mathbb{R}, \; c(x)$ は正則関数）

のように $x=p$ の周りでテイラー展開すると

$\begin{align*} (x-p)g(x) &= (x-p)(a + b(x-p) + c(x)(x-p)^2) \\ &= a(x-p) + b(x-p)^2 + c(x)(x-p)^3 \\ & \equiv a(x-p) \pmod{\mathfrak{m}_P^2} \end{align*}$

となります。剰余類の代表元としては $a(x-p)$ の形の多項式だけ考えれば十分だとわかります。

もう一度言い換えると、ベクトル空間 $\mathfrak{m}_P / \mathfrak{m}_P^2$ の各点は「1次関数 $a(x-p)$ （ $a$ は定数）に点 $P$ で接する有理関数全体」を表す剰余類ということになります。

結局、 $\mathfrak{m}_P / \mathfrak{m}_P^2$ の各点は「1次関数の傾き」だったわけですね。そして、 $\mathfrak{m}_P / \mathfrak{m}_P^2$ は「1次関数の傾き全体」のなす1次元ベクトル空間だったというわけです。

ところで、 $\mathfrak{m}_P / \mathfrak{m}_P^2$ を「余接空間」と呼んでいましたが、どの辺が「余接空間」なのでしょうか。実際に、これが多様体的な意味での余接空間 $T_P^{*}(X)$ と関係するのですが、それを確認してみましょう。

$f \in \mathfrak{m}_P$ に対して、 $(df)_P \in T_{P}^*(X)$ を与える写像 $d\colon \mathfrak{m}_P \to T_{P}^*(X)$ は、次の2つの性質を満たします：

①線形性： $a, b \in \mathbb{R}, \; f, g \in \mathfrak{m}_P$ に対して $( d(af + bg) )_P = a (df)_P + b (dg)_P$
②ライプニッツ則： $f, g \in \mathfrak{m}_P$ に対して $( d(fg) )_P = f(P) (dg)_P + g(P) (df)_P$

①により、 $d$ が線形写像であることがわかります。

また、 $f \in \mathfrak{m}_P$ を $x = p$ の周りでテイラー展開します。定数項が $0$ であることから

$f(x) = a_1(x-p) + g(x)(x-p)^2$ （ $g(x)$ は点 $P$ で正則な関数）

と表すことができます。また、ライプニッツ則から

$\begin{align*} d(g(x)(x-p)^2)_P &= g(x)(x-p)|_{x=p} d( x-p )_P + (x-p)|_{x=p} d( g(x)(x-p) )_P \\ &= 0 \end{align*}$

であるので、 $d$ によって $f$ の2次以降の項も消えます。したがって、 $(df)_P = 0$ ならば $a_1 = 0$ が導かれます。すなわち、 $d$ の核は $\mathfrak{m}_P^2$ となります。

$T_{P}^*(X)$ が1次元より、 $d$ が全射であることもわかります。したがって、準同型定理より

$\mathfrak{m}_P / \mathfrak{m}_P^2 \; \simeq \;T_{P}^*(X)$

なる同型が得られます。これで、 $\mathfrak{m}_P / \mathfrak{m}_P^2$ を余接空間だと思っても差し支えなさそうです。

この $\mathfrak{m}_P / \mathfrak{m}_P^2$ の双対空間 $(\mathfrak{m}_P / \mathfrak{m}_P^2)^*$ のことをザリスキー接空間というそうです。

まとめると、数直線 $\mathbb{R}$ 上の各点 $P$ には、それぞれ $\mathfrak{m}_P / \mathfrak{m}_P^2$ （あるいは $(\mathfrak{m}_P / \mathfrak{m}_P^2)^*$ ）という「直線の傾き全体」を表す1次元の余接空間（あるいは接空間）が乗っているような、ベクトルバンドル（ベクトル束）だと思うことができそうです。また、余接空間の各点は「原点を通るある直線に点 $P$ で接する多項式全体」がいることになっているわけですね。

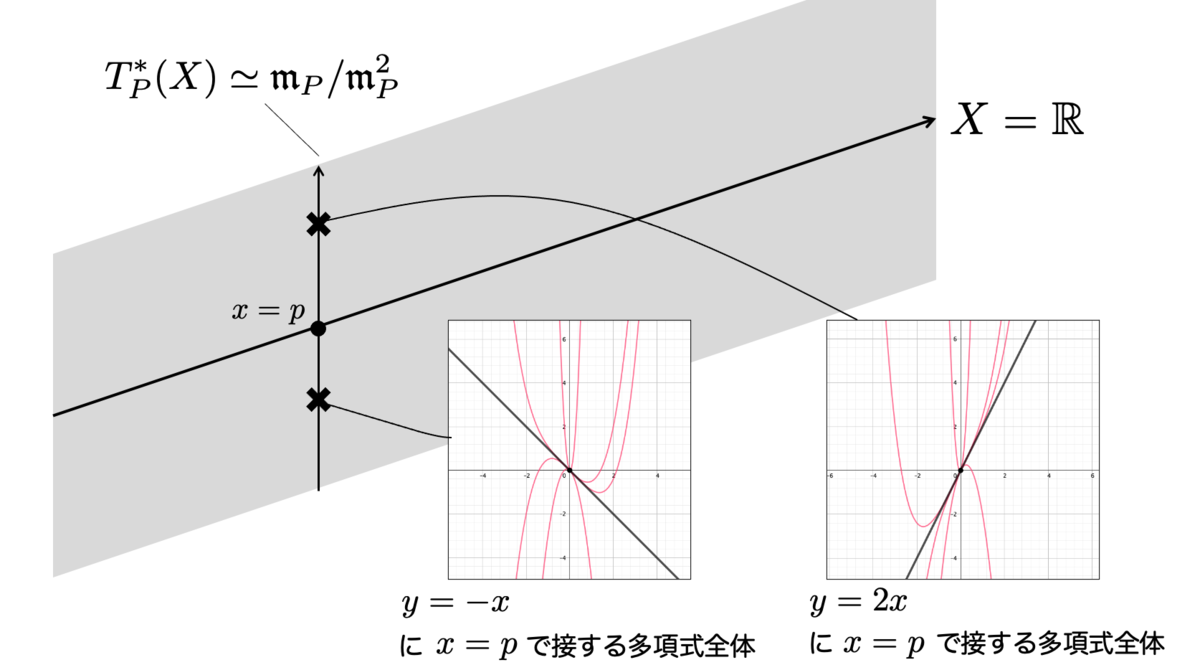
接空間だと思うことによって、かなり幾何的なイメージが湧いてきますね。いやー面白いな。

6. おわりに

共通テストの１つの大問から始まった今日の記事でしたが、考えてみると想像以上に深掘りできて、面白いですね。

とくに $\mathfrak{m}_P / \mathfrak{m}_P^2$ という空間は、私が勉強している代数曲線の文脈でも出てきます。初めは何のことかさっぱり分からない対象だったのですが、今回の調査を通して親しめそうな実感が湧いてきました。

最近勉強している「多様体の接空間」とも接点があって、とても面白かったです。

tsujimotterは今回やったように「高校で勉強した素朴な数学」が、大学以降に教わる専門的な数学を用いて、深い概念へと昇華されるのを見るのが好きです。高校数学というのはそれだけで独立した世界なのではなく、実際は専門的な数学とも地続きであるわけです。こうしたつながりを理解できるようになると、より専門的な数学も学んでみようかなという気にさせられます。

それでは今日はこの辺で！

おまけ

「Zariski tangent space」で検索してみるとこんなツイートと返信が

Take a polynomial, divide by (x-a)², and the remainder is the tangent line at x=a. Magic!https://t.co/mjW8m6BMqd
— Patrick Honner (@MrHonner) 2020年10月7日

This is the basic idea behind Zariski's algebraic definition of the tangent space. Useful for studying splines (smoothly joined piecewise polynomials) over tessellations.
— Vaitkus Márton (@vm_braindumps) 2020年10月7日