リーマンの素数公式の可視化アプリがパワーアップしました

「花の金曜日」ということで、前々から懸案事項だった数学アプリの整備を再開しました。言わば、

「一人数学ハッカソン」

です。

今回のテーマは「リーマンの素数公式」について。

実はこのテーマは、以前の記事でも扱ったテーマでした。

ちなみに、記事が長くて探しにくいと思うので、以前のバージョンのサイトへのリンクも掲載しておきます。

リーマンの素数公式を可視化する

以前のバージョンでは、canvas を使っているのでグラフの見た目があまりよくありませんでした。また、横に長いのでスマホだと見づらい、という難点もありました。

そこで、今回の一人数学ハッカソンで、改善させました。

完成品

完成品がこちらです！

スクリーンキャプチャはこんな感じ。

f:id:tsujimotter:20150109234845p:plain:w400

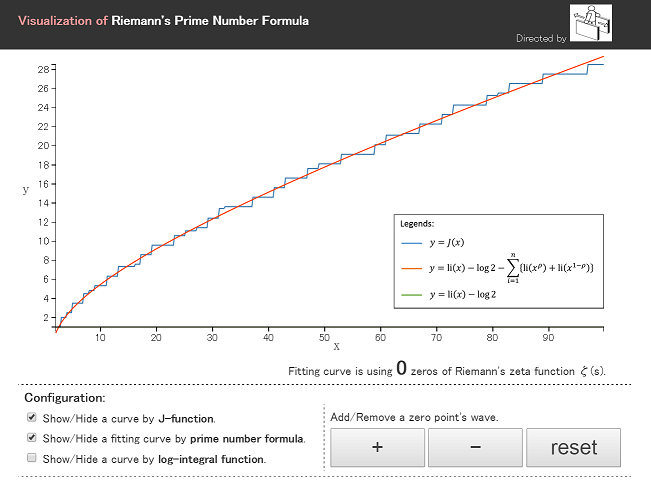
一番変わった点は、見た目のかっこよさです！！以上！！（笑）

変更点

中身の方にも、ちょっとだけマイナーチェンジがありました。

まず、グラフは ccchart.js から d3.js へと変更しました。具体的には、canvas (ラスター) から svg (ベクター) に変わったので、見た目がきれいになっています。あと、アニメーションが動きます。

数学的にも、いくつか変えた点があるので補足しておきます。

前回は、素数計数関数 $\pi(x)$ を使っていましたが、今回は $J(x)$ を使っています。これは、表記は違いますが、リーマンの原論文でも使われた関数です。これを使うと、素数公式の式が著しく簡単になるのです。

$J(x)$ の定義はこちら。

$\displaystyle J(x) = \pi(x) + \frac{1}{2}\pi(x^{\frac{1}{2}}) + \frac{1}{3}\pi(x^{\frac{1}{3}}) + \frac{1}{4}\pi(x^{\frac{1}{4}}) + \frac{1}{5}\pi(x^{\frac{1}{5}}) + \cdots \tag{1}$

$J(x)$ のイメージは $\pi(x)$ と比べて考えればわかりやすいです。素数計数関数 $\pi(x)$ は、素数 $p$ のときだけ $1$ 上がるような関数でした。一方 $J(x)$ は、素数 $p$ のときだけでなく、 $p^m$ のときもピコーンと $\frac{1}{m}$ だけ上にあがるような関数です。

この関数 $J(x)$ に対して、以下のような式が得られます。

$\displaystyle J(x) = {\rm li}(x) - \log 2 + \int_x^{\infty}\frac{{\rm d}t}{t(t^2 - 1) \log t} - \sum_{k=1}^{\infty} \left\{ {\rm li}(x^{\rho_k}) + {\rm li}(x^{1-\rho_k}) \right\} \tag{2}$

これがリーマンの素数公式です。等式は厳密に成立します。

${\rm li}(x)$ は対数積分（log-integral）といって、定義は次の通りです。

$\displaystyle {\rm li}(x) = \int_{0}^{x} \frac{{\rm d}t}{\log t} \tag{3}$

ただし上の積分は、積分範囲に特異点を持つため通常の意味での積分はできません。この場合は「コーシーの主値」と呼ばれる以下のような積分によって定義されます。

$\displaystyle \int_{0}^{x} \frac{{\rm d}t}{\log t} = \lim_{\varepsilon \to +0} \left\{\int_{0}^{1-\varepsilon} \frac{{\rm d}t}{\log t} + \int_{1+\varepsilon}^{x} \frac{{\rm d}t}{\log t} \right\}\tag{3'}$

実際に計算するときは上の式では面倒なので、「指数積分」と呼ばれる関数の級数を使って間接的に計算しています。

さて、(2) の式の後半の難しそうな和を取っ払えば、こんな式のように簡単に近似されます。

$\displaystyle J(x) \approx {\rm li}(x) - \log 2 + \int_x^{\infty}\frac{{\rm d}t}{t(t^2 - 1) \log t} \tag{4}$

もちろん、このままでは素数の細かい階段は再現されません。でもざっくりとした見積りとしてはこれで十分でしょう。これが、ガウスの素数定理です。ちなみに第３項目は、計算してみるとわかりますが、ほとんど全体に寄与しません。したがって、結局のところ $J(x)$ は対数積分で近似できるわけです。

そして、一番最後の項は「振動項」と言って、リーマンのゼータ関数の零点がつくる「振動の波」を表しているのでした。これがずらっと和になっていて、１つずつ足していくと、だんだんと対数積分が階段の形に近づいていく訳です。最終的には、これが $J(x)$ に一致します。これが面白いのです。

使い方

画面右下の「＋」のボタンをクリックしていくと、振動の波が足し合わされていきます。２０個ぐらい足すと、ほとんど $J(x)$ と区別つかなくなりますよ。ぜひ体験してみてください。

「reset」ボタンを押すと、足し合わさった波がすべて消えるので、今までのどれだけ積み重ねてきたのかが実感できるかと思います。

どのグラフを表示させるかは、左下のチェックボックスで選べます。好きなグラフを表示させてスクリーンショットをとれば、オリジナルの図が簡単に作れます。

というわけで、tsujimotterは十分遊んだので今日はこの辺で。
あー、プログラミング楽しかった。

2015/02/05追記:
対数積分に関する説明が不正確だったので修正しました。

参考文献・関連記事

[1] リーマンの素数公式を可視化する - tsujimotterのノートブック
前回 tsujimotter が解説した記事です。

[2] Riemann, B. (1859), "On the Number of Prime Numbers less than a Given Quantity". の日本語訳
こういう日本語訳がちゃんとウェブ上に上がっているのはありがたいですね。訳者に感謝です。

[3] Riesel, H. and Gohl, G. (1970), "Some Calculations Related to Riemann's Prime Number Formula", Mathematics of Computation, Vol. 24, No. 112, 969-983.
「振動項」の計算に使いました。タイトルで検索すれば PDF が無料で見れます。

[4] Odlyzko, A., "Tables of zeros of the Riemann zeta function".
いつもお世話になっている、素数の零点分布の「モンゴメリー・オドリツコ予想」で著名な Andrew Odlyzko 先生のウェブサイトです。1 から 100,000 までの零点がリストで並んでいます。

[5]