今日は3月31日ということで、331にまつわる小ネタを。
はじめに
4n+1の形で表せる素数はすべて平方数の和でただ一通りに表せる。
逆に平方数の和で表せる奇素数はすべて4n+1型である。
というのは、この記事で以前お話したことでした。
今日は 3n+1型 の素数に対しても同じような性質があることを紹介しましょう。
3n+1型の素数
3n+1の形で表せる素数 はすべて次のような和の形でただ１通りに表せます。
定理：3n+1型 の素数
は次のように和の形でただ１通りに表現できる。
ただし、
,
は互いに素な整数。
逆に、上記の形式で表せる素数は 3n+1型 または 3 となっています。
実例
実例を挙げましょう。
最も小さい 3n+1型素数 は 7 です。
もちろん 331 も 3n+1型素数 です。
ちなみにこんな巨大な数でもうまくいきますよ。
これだけ大きいと、カンマを付けないとよくわからなくなってしまいますね。
8n+1, 8n+3, 8n+7型の素数
4n+1型や3n+1型があるなら、ほかにもan+b型で似たようなことができるんじゃないの？と思った方、鋭いです。
次のような素数でも、平方数を使った和の形で表すことができるのです。
定理：8n+1型, または, 8n+3型 の素数
ただし、
定理：8n+1型, または 8n+7型 の素数
ただし、
例：
41 (8n+1型):
43 (8n+3型):
31 (8n+7型):
331 (8n+3型):
331は 8n+3型でもあったのですね。
素数チェッカー
「え、たまたまうまいこといくような素数を選んだだけじゃないかって？」
そんな疑りぶかいあなたは、ぜひ自分で計算してみてください。新たな発見があるかもしれません。
とはいえ、今回の記事のような素数を自分で探すのはなかなか大変ですよね。計算練習になるかもしれませんが。
そんなとき、ある整数を与えたら、それが素数かどうか判定してくれて、なおかつ 3n+1 や 8n+1 のときにうまいこと平方和で分割してくれるようなアプリがあったら便利ですよね。
そんな便利なアプリないかなー・・・ないかなー・・・（チラッ）
なんと、あったじゃないですかー！
やだなー、もー、早く言ってくださいよ。
スクリーンショットなんかとっちゃいましたよー。
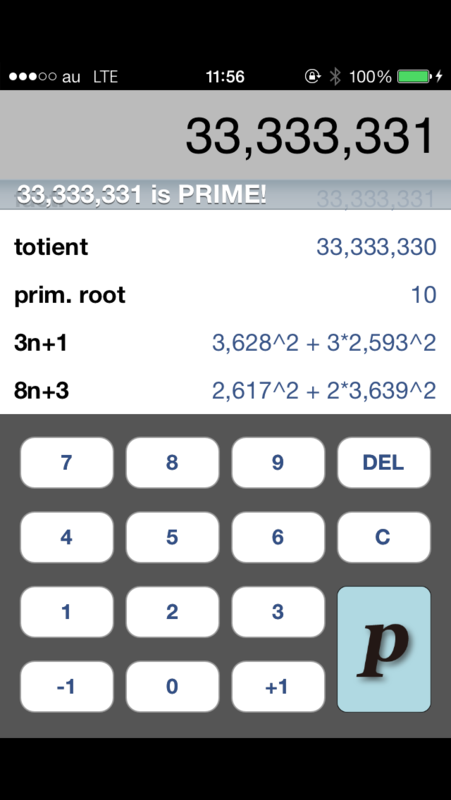
「+1」, 「-1」 という便利キーもついていて、次の数が素数かどうかも確認できちゃいますね。
これで、317の次の素数が331であることがすぐにわかってしまいます。
便利ですね～。
・・・・
・・・・
ということで、私が作ったわけじゃないですが、つい宣伝してしまいました。
よろしかったら遊んでみてくださいな。
それではこの辺で。
