以前「足し算の繰り上がりと群コホモロジーが関係している」という話が、Twitter上で話題になったことがありました。
もうちょっと説明してくれといわれたので、しますと、Z/100Z は mod 100 の整数が足し算のもとでなす群ですが、その中で10の倍数は Z/10Z (すなわち10の位) と同型な部分群をなして、商群も Z/10Z (すなわち1の位)になります。だから、Z/100Z は1の位のなす Z/10Z を10の位のなすZ/10Zで拡大したもの。
— 🥑 (@yujitach) 2017年11月16日
関連するツイートとして、次のようなものもありました。
nLabの記事(同じ論文を引用してます):https://t.co/IRAOYBB7yU
— Iwao KIMURA (@iwaokimura) 2019年10月14日
当時は理解できなかったのですが、久しぶりに思いだして自分なりに考えてみたところ、結構理解できた部分がありました。せっかくなのでまとめてみようと思って書いています。
「こんなところに群コホモロジーが関連してくるの!?」というところを楽しんでいただければと思います。
tsujimotter.hatenablog.com
特にこの2つの記事が関係すると思います。
tsujimotter.hatenablog.com
二進法の足し算
元の話では十進法の足し算で考えていましたが、十進法は組み合わせが多くて難しいので、今回は 二進法の足し算 に限定して考えたいと思います。
(まったく同じ考え方で十進法も考えることができますのでご安心ください。)
二進法で一桁の足し算を考えるとき、次の4通りを考えれば十分です:
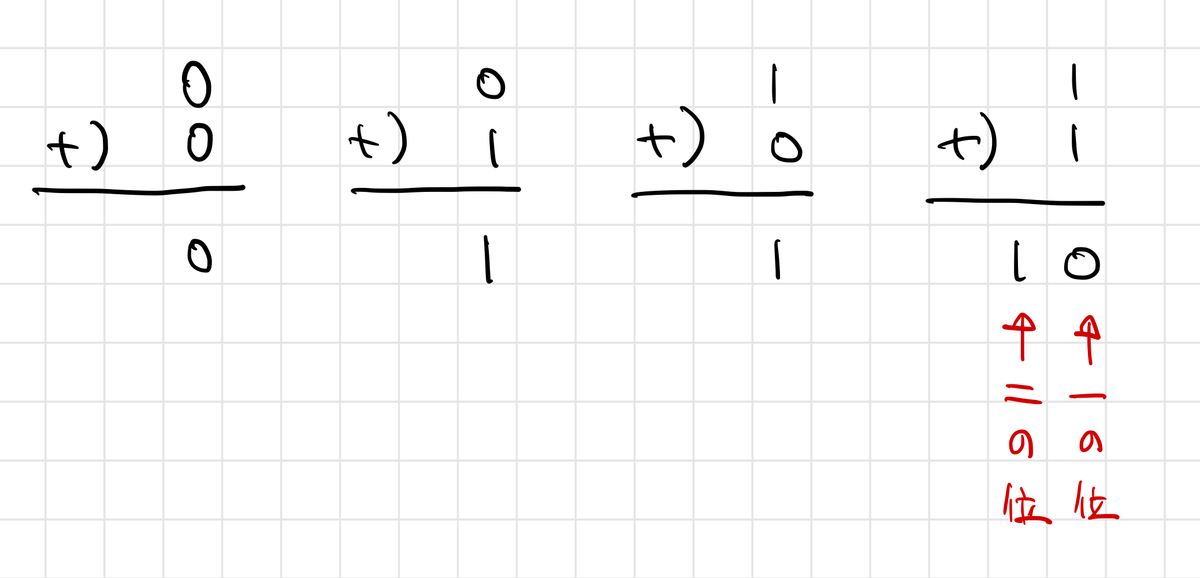
一の位の計算は「 の足し算」になりますので、
の普通の足し算を考えればよいでしょう。
一方で二の位(十進法でいうところの十の位)の部分、これを 繰り上がり と言います。「繰り上がりの計算はいったいどのように解釈できるでしょうか?」というのが今回のテーマです。
少しフォーマルに書くと、繰り上がりの計算は (一の位)の2つの元に対して、
(十の位)の元を与える写像だと思うことができます。
すなわち、写像 を次のように定めるということです:
引数にあたる は一の位、行き先にあたる
は十の位に対応することに注意します。(少しややこしいですね。)
実は、この写像 は 2-コサイクル であるという性質を持っています。
が2-コサイクルであるとは、任意の
に対し、
が
を満たすことを言います。
実際、8通りすべてに対して、成り立つことが以下の表からわかります(ぜひ皆さんも確認してみてください):
というわけで、繰り上がりの写像 が2-コサイクルであった、というのが一つ目の結論です。
群の拡大
なんで、2-コサイクルが出てくるのか、という点をもう少し掘り下げていきましょう。
ここには 群の拡大 というものが関係しています。一般に群の拡大とは、短完全列:
のことを指します。(あるいは、 を主役にして、
のことを
の
による群の拡大、ということもあります。)
特に、 をアーベル群とし、
の
による中心拡大と呼ばれるものを考えます。中心拡大とは、式
の短完全列において、
が
の中心(center)に入っていることをいいます。
今回は、 としてすべてアーベル群を考えているので、この仮定は自動的に満たされています。
さて、今回のケースにおいては、次のような群の拡大を考えることになります:
これから式 の意味を説明していきますが、
が2つ出てきて少しわかりづらいですね。群の拡大
の記号を用いて「
の方の
」とか、「
の方の
」というように呼んでいきたいと思います。
まず ですが、二進法2桁の数
を表す加法群です。
ここからは の元をずっと二進法により表すことにします。
次に「 の方の
」ですが、これは「二の位の値」を表します。二の位は「二進法2桁の数」として考えるとき
と対応しますが、これがちょうど2倍写像になるわけですね。これにより2倍写像
が定まるというわけです。集合の元の対応関係を図に表すと
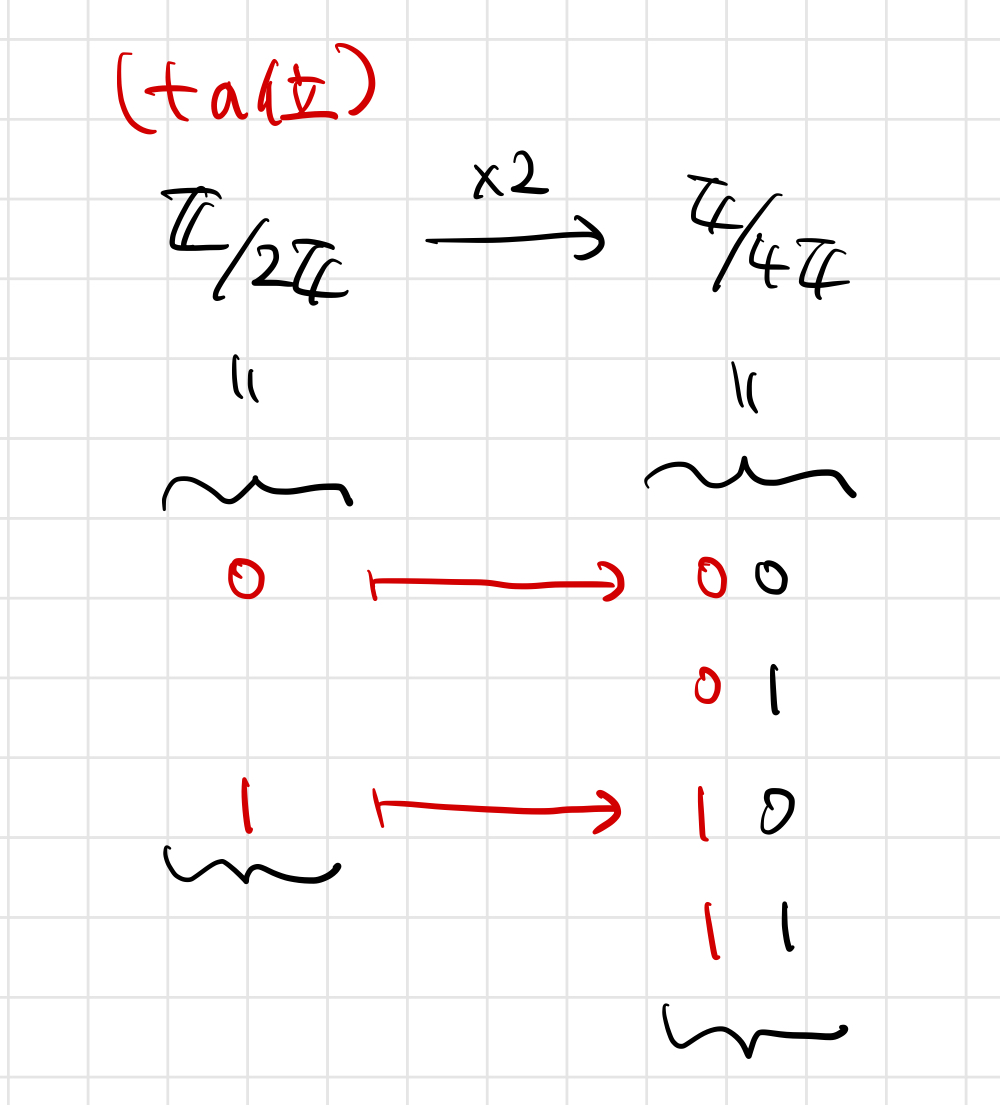
ということになります。
今度は「 の方の
」ですが、こちらは「一の位の値」を表します。これは2倍写像のCokerになっていて、2倍写像で送った「
の方の
」で
を割った群となります。
この群の割り算は「二の位を無視して、一の位が同じものを同一視する」ことに相当するので、 写像であったというわけですね:
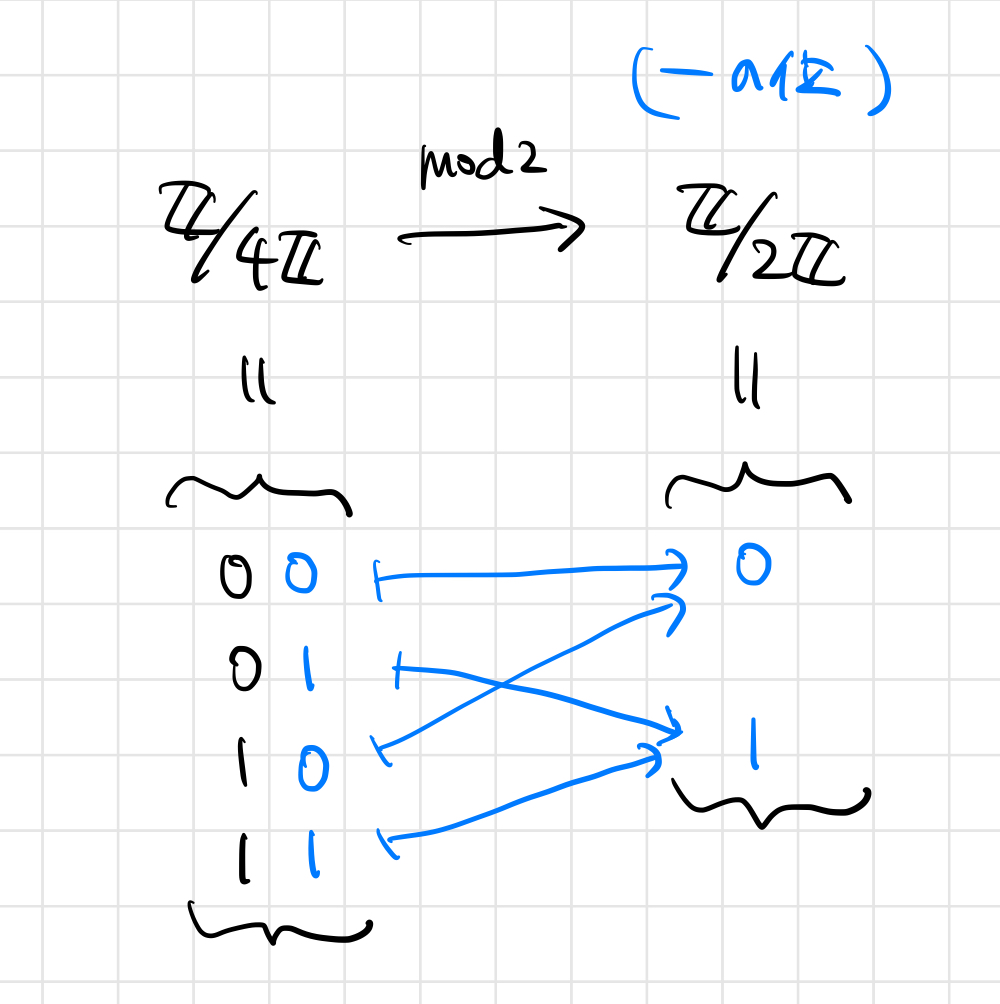
以上により、群の拡大 の全容がわかったかと思います。図に表すとこうなります:

二進法2桁の足し算とは、 における群演算を考えていることに他なりません。
群の拡大 の演算を、一の位
と二の位
によって記述するのが繰り上がりの演算だったと考えることができるでしょう。
ところで、 の
による群の拡大としては、もう一つ
が考えられると思います。
しかし、この拡大は二進法の足し算には対応しません。なぜならば、二進法2桁の足し算は の足し算にはならないからです。実際、
の足し算は
ですが、二進法の足し算が
になったらおかしいですよね。
群の拡大と2-コサイクル
いよいよ群の拡大と2-コサイクルの関係について説明しましょう。一般に、群の拡大が与えられると、そこから2-コサイクルを導く具体的な手順があるのです。
まず、群の拡大
に対して、切断 を考えます。
切断とは、 となるような
のことです。
は
から
への「一方通行」ですが、逆に
の元を
に持っていく写像を考えたいということですね。ただし、
から
に戻したものを、再度
で送ったときに元に戻って欲しい、という条件が付いています。
実際、群の拡大
に対して、切断 (定義域は
の方の
)を次のように定めます:
定義域の は「一の位」を表しますので、これをそのまま二進法の数に埋め込んだ感じですね。
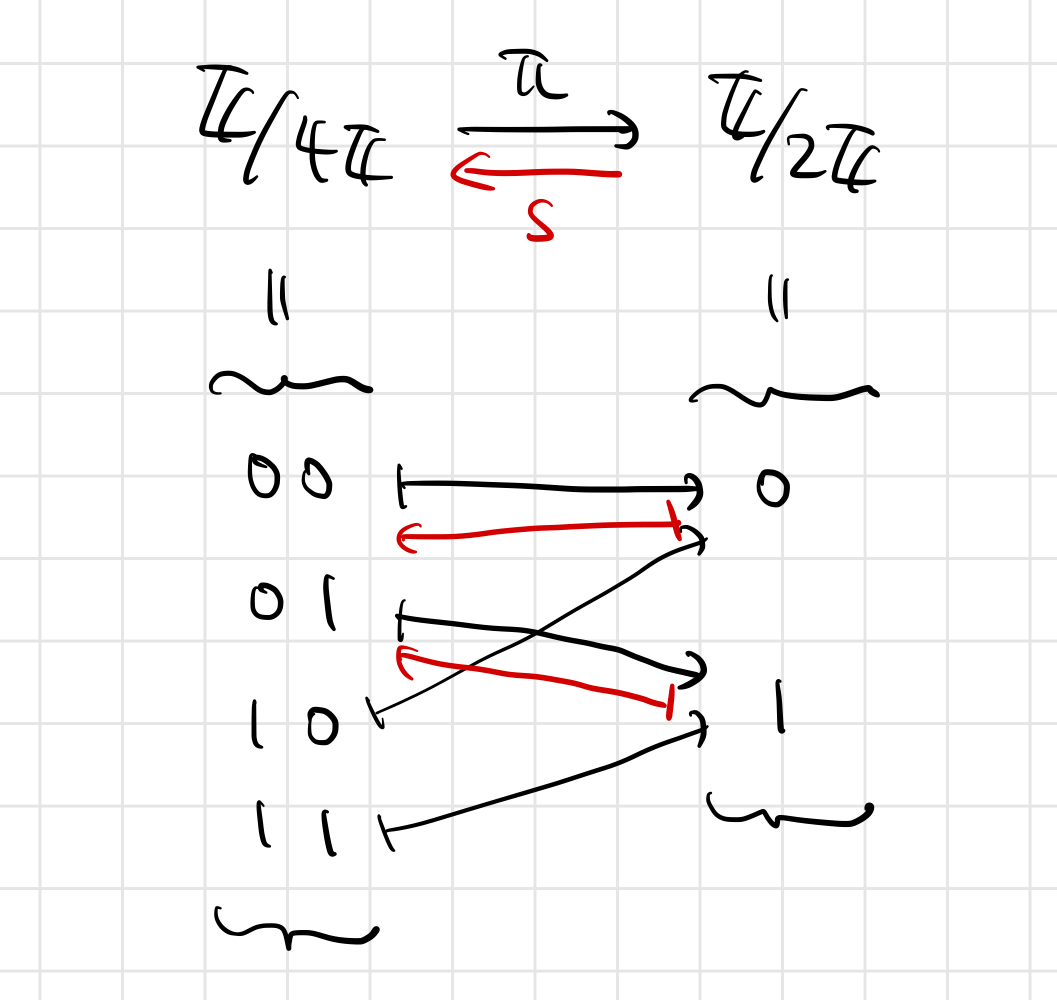
二の位を二倍写像 で送ったものを
とし、一の位の元を
で送ったものをそれぞれ
とします。
これらを用いて を、次のように表すことができます:
要するに一の位と二の位を別々に考えている感じですね。
この集合の中で、1桁の数同士の演算を考えます:
たとえば2行目でやっていることは
を足し合わせると、 となり、これは
になるよ、という計算をやっていることになります。
単に1桁同士の数の和を計算しているだけなのですが、記号を変えると途端によく分からなくなりますね。
ここで、太字で書いた部分 を
で戻して並べて
とします。これを用いて写像
を作ります:
この写像 が群の拡大
から作られる2-コサイクルとなります。実際、2-コサイクルになっていることは計算すればすぐにわかります。
というかそもそも作り方からして、 (一の位)の2つの元に対して、
(十の位)の元を与える写像だったわけで、これは繰り上がりの写像そのものですね!!
繰り上がりの写像が2-コサイクルになっていることは先ほど確認したので、これは当然2-コサイクルになっているわけです。
もっというと、一般に群の拡大(中心拡大)
に対して、まったく同様の手順で写像 を作ることができます。これが2-コサイクルになることは一般的に言えるので、このことから繰り上がり写像が2-コサイクルであったというわけなんですね。
こんな仕組みが裏にあったというわけです。面白いですね!
ここまでの話は
という話でした。
逆方向もいうことができます。
足し算の例でいうと、与えられているものは群 (一の位)、
(ニの位)および2-コサイクル
でした。
ここで、集合として を
で定めます。(あくまで、集合としてなので、この段階では演算は考えていません。)
この集合に、次のような「加法」の演算を入れます。(二の位)、
(一の位)に対し
とします。下線部分の がなければ単なる直積
の加法なわけですが、下線の部分が入ることによって、ニの位の計算に一の位からの「繰り上がり」が入ってきたことになるわけです。これによって、
の加法の演算が復元されたというわけなのですね。
2次の群コホモロジーとの関係
最後に、群コホモロジーとの関係について触れておきます。
2-コサイクルといえば、2次の群コホモロジーの元なのでした。より正確にいえば、2次の群コホモロジーとは2-コサイクル全体を2-バウンダリ全体で割った群のことでした。
なので、2-コサイクルの同値類が2次の群コホモロジーの元というわけですね。
一方、群の拡大の方にも、同型を考えることができます。適切に同型類を定めることによって、次の事実が一般に成り立ちます:
今回のケースでいうと、2次の群コホモロジー は位数2となっています。つまり、自明な元と非自明な元があるわけです。
群の拡大
に対応する2-コサイクル (繰り上がり写像)は、非自明な元に対応します。
一方で、
の方は、自明な2-コサイクルに対応するようです。
の元としては、この2つだけということですね!
まったく同じように、群の拡大
に対して、上と同じ手順で2-コサイクル与えると、十進法1桁の足し算における繰り上がりを与えることができるはずです。興味がある人はぜひ考えてみてください。
小学校で習った足し算の繰り上がりって、数学的にはこんなに深かったのですね!
それでは今日はこの辺で!
参考文献(2021.03.12追記)
まだ最初の方しか読めてないのですが、こちらの論文が基本的な文献かと思います。
A Cohomological Viewpoint on Elementary School Arithmetic
Daniel C. Isaksen
https://www.jstor.org/stable/3072368
補足(2021.03.12追記)
における加法の結合則を考えると、2-コサイクル条件は自然に出てくることに気づいたので、こちらに載せておきます:
(画像ですみません。)
