複素射影直線 ℙ¹ はコンパクトリーマン面

以下の記事でリーマン面の定義をまとめたことがありました。
tsujimotter.hatenablog.com

これまでtsujimotterのブログではリーマン面の具体例を挙げたことがありませんでした。今日は、リーマン面（特にコンパクトリーマン面）の代表例である複素射影直線 $\mathbb{P}^1$ を紹介します。 $\mathbb{P}^1$ が、リーマン面の構造を持つ例であることを、リーマン面の定義にしたがって示したいと思います。

f:id:tsujimotter:20210308133520p:plain:w300

なお、リーマン面の定義は示すべき条件が割と多く、証明を丁寧にやろうとすると結構大変です。大変ではあるのですが、示す価値はあります。リーマン面であることを示すことにより、リーマン面に成り立つ諸定理を使うことができるのですね。一般に、定義の条件が示しづらいほど、使うときには強力な武器となることが多いのではないかと思います。

今回は、解説記事というよりは、tsujimotterの勉強した成果をまとめておくというのが主な目的です。

普段のtsujimotterのノートブックでは、分野外の人にもなるべく理解してもらえるように前提知識の説明を丁寧に行っているのですが、今回はただでさえ証明が長いのでそれをやるのは難しいです。最低限の解説を述べつつ、あくまで証明が中心という形の内容としたいと思います。

目次：

1. ℙ¹の定義

1-1. ℙ¹の定義

1-2. ℙ¹の位相

1-3. ℙ¹の開被覆とアトラス

1-4. 証明したい主張

1-5. コンパクト性の定義

2. ℙ¹はコンパクトリーマン面の証明

2-1. U₀, U₁ は ℙ¹ の開集合

2-2. φ₀, φ₁ は同相写像

φ₀ の単射性

φ₀ の全射性

φ₀ の連続性

φ₀⁻¹ の連続性

2-3. 座標変換が正則関数

2-4. 正則行列によって表せる ℙ¹ から ℙ¹ への同相写像

2-5. ℙ¹ は第2可算公理を満たす連結かつコンパクトなハウスドルフ空間

ℙ¹ は第2可算公理を満たす

ℙ¹ は連結かつコンパクト

ℙ¹ はハウスドルフ

3. 参考文献

1. ℙ¹の定義

まず、複素射影直線 $\mathbb{P}^1$ を定義します。

1-1. ℙ¹の定義

$\mathbb{C}^2 \setminus \{ (0, 0) \}$ の2点 $(x_0, x_1), \; (y_0, y_1)$ に対して、次で定まる同値関係を入れます：

$(x_0, x_1) \sim (y_0, y_1)$ $\Longleftrightarrow$ ある $\mathbb{C} \setminus \{0\}$ が存在して $(x_0, x_1) = (cy_0, cy_1)$

すなわち、定数倍して一致する点は同じものとみなすわけですね。

「比」が同じになる2点を同一視しているということですね。

$\mathbb{C}^2 \setminus \{ (0, 0) \}$ を同値関係 $\sim$ で割った集合を複素射影直線と言い、 $\mathbb{P}^1$ と書くことにします。

$\mathbb{P}^1 := \mathbb{C}^2 \setminus \{ (0, 0) \} \; \big/ \;\sim$

$\mathbb{P}^1$ は $\mathbb{CP}^1$ 、 $\mathbb{P}^1_{\mathbb{C}}$ 、 $\mathbb{P}^1(\mathbb{C})$ 等と書くこともありますが、今回は $\mathbb{P}^1$ で統一します。

$\mathbb{P}^1$ への全射

$\pi \colon \;\; \mathbb{C}^2 \setminus \{ (0, 0) \} \; \longrightarrow \; \mathbb{P}^1$

を考え、これを商写像と呼ぶことにします。 $\pi$ による $(x_0, x_1) \in \mathbb{C}^2 \setminus \{ (0, 0) \}$ の像を $[x_0 : x_1]$ と表すことにします。これを同次座標といいます。

$x_0$ と $x_1$ の「比」に興味があるので、比のような書き方をしているわけです。

1-2. ℙ¹の位相

次に、 $\mathbb{P}^1$ に位相を入れたいと思います。

まず、 $\mathbb{C}^2$ を $\mathbb{R}^4$ だと思ったときに、ユークリッド距離による位相が入ります。 $\mathbb{C}^2$ の部分集合 $U$ 内の任意の点 $x$ に対して、 $x$ を中心とする半径 $\varepsilon > 0$ の開球が存在するとき、 $U$ を $\mathbb{C}^2$ の開集合であるとします。このように定義されたもの全体を開集合とする位相空間（距離位相空間）を考えるわけです。

$\mathbb{C}^2 \setminus \{ (0, 0) \}$ は $\mathbb{C}^2$ の部分集合なので、相対位相が入ります。すなわち、 $\mathbb{C}^2$ の任意の開集合 $U$ に対して $U\cap \mathbb{C}^2 \setminus \{ (0, 0) \}$ を $\mathbb{C}^2 \setminus \{ (0, 0) \}$ 開集合とするわけです。

続いて、先ほどの商写像 $\pi$ を考えます。

$\pi \colon\;\; \mathbb{C}^2 \setminus \{ (0, 0) \} \; \longrightarrow \; \mathbb{P}^1$

$\mathbb{P}^1$ の部分集合 $U$ が $\mathbb{P}^1$ の開集合であるとは、 $\pi$ による逆像 $\pi^{-1}(U)$ が $\mathbb{C}^2 \setminus \{ (0, 0) \}$ の開集合であることをいいます。

つまり、 $\mathbb{P}^1$ の任意の開集合 $U$ の $\pi$ による逆像 $\pi^{-1}(U)$ はすべて $\mathbb{C}^2 \setminus \{ (0, 0) \}$ の開集合であるというわけです。すなわち、 $\pi$ はこの位相において連続写像です。

逆にいうと、 $\pi$ が連続になるような $\mathbb{P}^1$ の位相の中で、もっとも開集合が多い位相になっているということですね（最強の位相）。このような位相を商位相といいます。

ここで、 $\mathbb{P}^1$ の開集合を減らしたとして、 $\pi$ は連続写像のままであることに注意しましょう。「値域の開集合の逆像が定義域の開集合」という連続性の条件が、より簡単になるからですね。なので、連続写像のままであるような、ギリギリ一番開集合の多いものを選んで商位相の定義とするわけです。

これによって、 $\mathbb{P}^1$ の位相が定まりました。

ここで、商位相の性質を思い出します。

まず、これは一般の連続写像になりたつ性質ですが、連続写像 $f\colon X \to Y, \;\; g\colon Y \to Z$ の合成写像 $g\circ f \colon X \to Z$ は連続写像になります。

したがって、ある連続写像 $\pi\colon \mathbb{C}^2 \setminus \{ (0, 0) \} \to \mathbb{P}^1$ と $\mathbb{P}^1$ からの連続写像 $f\colon \mathbb{P}^1 \to Z$ との合成

$f \circ \pi \colon \; \mathbb{C}^2 \setminus \{ (0, 0) \} \xrightarrow{ \; \pi \; } \mathbb{P}^1 \xrightarrow{ \; f \; } Z$

は連続写像となります。

逆に、連続写像 $g\colon \mathbb{C}^2 \setminus \{ (0, 0) \} \to Z$ があったとします。 $g = f\circ \pi$ であるような位相空間の間の写像 $f\colon \mathbb{P}^1 \to Z$ が存在するとき、 $f$ は連続写像となります。これを商位相の普遍性といいます。

f:id:tsujimotter:20210308142801p:plain:w220

1-3. ℙ¹の開被覆とアトラス

$\mathbb{P}^1$ にリーマン面の構造を与えるために、 $\mathbb{P}^1$ の開被覆 $\mathbb{P}^1 = U_0 \cup U_1$ を次で定めます：

$U_0 := \{ [x_0 : x_1 ] \in \mathbb{P}^1 \; \mid \; x_0 \neq 0 \}$

$U_1 := \{ [x_0 : x_1 ] \in \mathbb{P}^1 \; \mid \; x_1 \neq 0 \}$

なお、 $[x_0 : x_1] \in \mathbb{P}^1$ が $x_0 \neq 0$ のとき、 $c \in \mathbb{C}\setminus \{(0, 0)\}$ に対する $[ cx_0 : cx_1 ]$ についても $cx_0 \neq 0$ であることがわかります。したがって、 $[x_0 : x_1] \in U_0$ のとき $[cx_0 : cx_1 ] \in U_0$ が成り立ちます。すなわち、 $U_0$ の定義は $[x_0 : x_1]$ の代表元の取り方によらない（well-definedである）ということですね。（ $U_1$ も同様です。）

開被覆であることをいうためには、 $U_0, U_1$ が $\mathbb{P}^1$ の開集合である必要がありますが、これは証明の2-1.で示すことにします。

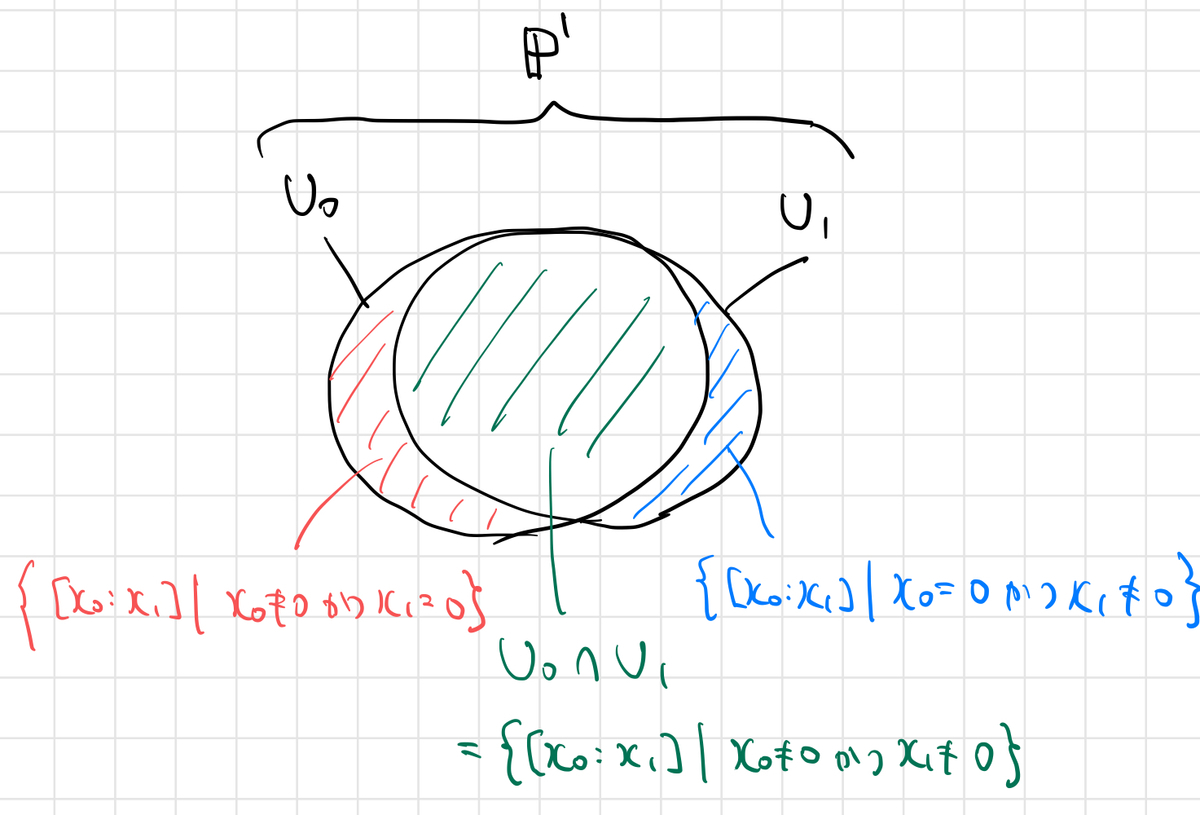
f:id:tsujimotter:20210308140201j:plain:w400

上の図では、 $\mathbb{P}^1$ を3つの部分

$U_0 \setminus U_1, \;\; U_0 \cap U_1, \;\; U_1 \setminus U_0$

に分けていますが、実際左右の2つの部分は1点集合です：

$U_0 \setminus U_1 = \{ [ 1 : 0 ] \}$

$U_1 \setminus U_0 = \{ [ 0 : 1 ] \}$

よって、大部分が $U_0$ と $U_1$ の「のりしろ」 $U_0 \cap U_1$ となっているような被覆を考えているわけですね。

また、次で定義される写像 $\varphi_0, \varphi_1$ を考えます：

$\displaystyle \begin{align} \varphi_0 \colon \;\;\;\; U_0 \;\;\;\; &\longrightarrow \;\;\, \mathbb{C}, \\ [x_0 : x_1] \;& \longmapsto \;\; \frac{x_1}{x_0} \end{align}$

$\displaystyle \begin{align} \varphi_1 \colon \;\;\;\; U_1 \;\;\;\; &\longrightarrow \;\;\, \mathbb{C}, \\ [x_0 : x_1] \;& \longmapsto \;\; \frac{x_0}{x_1} \end{align}$

ここで、 $[x_0 : x_1 ] \in U_0$ においては $x_0 \neq 0$ であるので、写像 $\varphi_0$ の行き先の値 $x_1 / x_0$ が定まることに注意しましょう。（ $\varphi_1$ も同様です。）

また、 $[x_0 : x_1] = [cx_0 : cx_1] \in U_0$ に対して、

$\displaystyle \varphi_0([x_0 : x_1]) = \frac{x_1}{x_0} = \frac{cx_1}{cx_0} = \varphi_0([cx_0 : cx_1])$

なので、 $\varphi_0([x_0 : x_1])$ の値は、 $[x_0 : x_1]$ の代表元の取り方によらないことがわかります。 $\varphi_0$ はwell-definedであるということです。

f:id:tsujimotter:20210308140243j:plain:w300

1-4. 証明したい主張

これにて準備が整いました。今回示したいのは次の定理です。

定理

$(\mathbb{P}^1, \; \{ (U_0, \varphi_0), \; (U_1, \varphi_1)\})$ はコンパクトリーマン面である。

この事実を以下で（一生懸命）示していきたいと思います。

単にリーマン面ではなく、コンパクトリーマン面であることも示します。位相空間としてコンパクトであるようなリーマン面をコンパクトリーマン面といいます。

コンパクト性の定義については次で述べますが、証明の過程でコンパクト性も簡単に示すことができるのです。

1-5. コンパクト性の定義

位相空間 $X$ がコンパクトとは、 $X$ の任意の開被覆 $X \subset \bigcup_{\lambda \in \Lambda} U_\lambda$ に対して、ある有限な部分被覆 $X \subset \bigcup_{i=1}^{n} U_{\lambda_i}$ を取れることを言います。

誤解されやすいですが、単に $X$ 有限開被覆を取れること自体がコンパクトの定義ではありません。

もし有限開被覆をとれるだけでコンパクトの定義になるのであれば、たとえば $\mathbb{C}$ の開被覆として $\mathbb{C}$ 自身をとってしまえば有限（1個の）開被覆になりますので、コンパクトになってしまいます。（念の為言っておくと、 $\mathbb{C}$ はコンパクトではありません。）

任意の開被覆に対し（当然、何でも良いので無限開被覆を考えてもよい）、その中から有限個のうまい開集合を選んで $X$ を覆うことができる。必ずそれができるというのがコンパクトの条件なわけですね。

定義から何となく察することができますが、証明するのはかなり大変です。なにせ、任意の開被覆を考えて、それに対して有限開被覆が取れるかどうか示さないといけないわけですからね。

逆に使う側としては非常に便利です。「任意の開被覆に対して〜」ということは、使うときは何か便利な開被覆をとってよいわけです。そしたら、コンパクト性の条件からいろんなことが導かれてしまうというわけです。

敵にすると手強いけど、味方にすれば心強い、みたいな感じですかね。

そんなコンパクト性なのですが、特定の条件を満たす場合においては簡単に言えてしまうのです。それが次の定理です：

有限次元ユークリッド空間の有界閉集合はコンパクト。

たまたま今回はこれを満たす状況が作れるということで、コンパクト性をあっさり示すことができます。これについては証明の中で実際にやってみればわかるかと思います。
（ $\mathbb{P}^1$ が直接この条件を満たすというわけではありません。）

2. ℙ¹はコンパクトリーマン面の証明

リーマン面の定義にしたがって、 $(\mathbb{P}^1, \; \{ (U_0, \varphi_0), \; (U_1, \varphi_1)\})$ がリーマン面であることを示します。特にコンパクトリーマン面であることを示します。

ただし、リーマン面の定義の記事で書いたような①〜⑦を順番に示すことはしません。（というか順番通りには示せません。）

2-1. 〜 2-5. の５つのパートに分けて順に示していくことにしましょう。

2-1. U₀, U₁ は ℙ¹ の開集合

まず、 $U_0, U_1$ が $\mathbb{P}^1$ の開集合であることを示したいと思いますが、そのために商写像 $\pi \colon \mathbb{C}^2 \setminus \{(0, 0)\} \to \mathbb{P}^1$ が開写像であることを示します。

$\pi$ が開写像とは、 $\mathbb{C}^2 \setminus \{(0, 0)\}$ の任意の空でない開集合 $V$ の像 $\pi(V)$ が $\mathbb{P}^1$ の開集合であることをいいます。

$\pi$ が開写像であることを使えば、次のようにして $U_0, U_1$ が $\mathbb{P}^1$ の開集合であることが言えます。

まず

$\tilde{U_0} := \{(x_0, x_1) \in \mathbb{C}^2\setminus \{(0, 0)\} \mid x_0 \neq 0\}$

$\tilde{U_1} := \{(x_0, x_1) \in \mathbb{C}^2\setminus \{(0, 0)\} \mid x_1 \neq 0\}$

とおきます。定義から $\pi(\tilde{U_0}) = U_0$ と $\pi(\tilde{U_1}) = U_1$ であることがわかります。

また、 $U_0$ の任意の点 $x$ に対して、 $x$ を含む十分小さな開球が取れるので $x$ は $U_0$ の内点です。よって、 $U_0$ は $\mathbb{C}^2\setminus \{(0, 0)\}$ の開集合です。 $U_1$ も同様です。

$\pi$ は開写像より、 $U_0 = \pi(\tilde{U_0})$ 、[tex; U_1 = \pi(\tilde{U_1})] は $\mathbb{P}^1$ の開集合です。

以下では、商写像 $\pi$ が開写像であることを示します。 $\mathbb{C}^2 \setminus \{(0, 0)\}$ の任意の空でない開集合を $V$ とし、 $V$ の像 $\pi(V)$ が $\mathbb{P}^1$ の開集合であることを示します。

$\pi(V)$ が $\mathbb{P}^1$ の開集合であることは、商位相の定義より $\pi^{-1}( \pi(V) )$ が $\mathbb{C}^2 \setminus \{(0, 0)\}$ の開集合であることと同値です。よって、これを示します。

$\mathbb{C}\setminus \{0\}$ の元 $c$ に対して

$cV := \{ (cx_0, cx_1) \; \mid \; (x_0, x_1) \in V \}$

とおきます。このとき、商写像 $\pi$ による $V$ および $cV$ の行き先は、ともに $\pi(V)$ となります。

$(x_0, x_1) \in \mathbb{C}^2\setminus \{(0, 0)\}$ に対して

$\pi^{-1}( \pi(x_0, x_1) ) = \pi^{-1}( [x_0, x_1] ) = \{ (cx_0, cx_1) \; \mid \; c \in \mathbb{C}\setminus \{0\} \}$

であり、これより

$\displaystyle \begin{align} \pi^{-1}( \pi(V) ) &= \bigcup_{(x_0, x_1) \in V} \{ (cx_0, cx_1) \; \mid \; c \in \mathbb{C}\setminus \{0\} \} \\ &= \bigcup_{c \in \mathbb{C}\setminus \{0\}} cV \end{align}$

となります。

一方、 $c$ 倍写像

$\begin{align} \mathbb{C}^2\setminus \{(0, 0)\} &\longrightarrow \mathbb{C}^2\setminus \{(0, 0)\}, \\ (x_0, x_1) \;\;\;\; &\longmapsto \;\; (cx_0, cx_1) \end{align}$

は同相写像です。

したがって、 $V$ が $\mathbb{C}^2\setminus \{(0, 0)\}$ の開集合であるならば、 $cV$ も $\mathbb{C}^2\setminus \{(0, 0)\}$ の開集合です。

よって、 $\pi^{-1}( \pi(V) ) = \bigcup_{c \in \mathbb{C}\setminus \{0\}} cV$ は開集合の合併なので、 $\pi^{-1}( \pi(V) )$ も $\mathbb{C}^2\setminus \{(0, 0)\}$ の開集合です。

$\pi^{-1}( \pi(V) )$ が $\mathbb{C}^2\setminus \{(0, 0)\}$ の開集合なので、商位相の定義より $\pi(V)$ は $\mathbb{P}^1$ の開集合であることが分かりました。したがって、 $\pi$ は開写像です。

以上により、 $U_0, U_1$ が $\mathbb{P}^1$ の開集合であることが示されました。

2-2. φ₀, φ₁ は同相写像

以下では、 $\varphi_0 \colon U_0 \longrightarrow \mathbb{C}$ が同相写像であることを示します。

$\varphi_0$ の単射性・全射性・連続性・ $\varphi_0^{-1}$ の連続性をそれぞれ示す必要があります。 $\varphi_0$ のwell-defined性は既に示しています。（ $\varphi_1$ も同様です。）

f:id:tsujimotter:20210308140532j:plain:w300

φ₀ の単射性

$\mathbf{x} = [x_0 : x_1], \; \mathbf{y} = [y_0 : y_1] \in U_0$ に対して

$\varphi_0(\mathbf{x}) = \varphi_0(\mathbf{y})$

が成り立っているとします。

このとき、 $\varphi_0$ の定義より

$\displaystyle \frac{x_1}{x_0} = \frac{y_1}{y_0}$

が成り立ちます。これより $x_1 = \frac{y_1}{y_0}x_0$ が成り立つことを使うと

$\displaystyle [x_0 : x_1] = [x_0 : \frac{y_1}{y_0}x_0 ] = [y_0 : y_1 ]$

が成り立ちます。最後の等号では、同次座標に $\frac{y_0}{x_0} \in \mathbb{C} \setminus \{0\}$ をかけても $\mathbb{P}^1$ の点は動かないことを使いました。

よって、 $\varphi_0$ は単射です。

φ₀ の全射性

任意の $y \in \mathbb{C}$ に対して、 $[1 \colon y] \in \mathbb{P}^1$ を考えると $\varphi_0([1 \colon y]) = y$ となります。

よって、 $\varphi_0$ は全射です。ここまでの議論で $\varphi_0$ が全単射であることが言えました。

なお、リーマン面であることを示すのに、一般には $\varphi_0\colon U_0 \to \mathbb{C}$ が全射である必要はありません（ $\mathbb{C}$ の中への写像であれば良い）。

今回はたまたま全射になっているということと、上で与えた逆写像を以降の議論で使うので、証明しています。後のために書いておくと

$\varphi_0^{-1}(y) = [1 \colon y]$

というわけですね。これは逆写像になっています。

φ₀ の連続性

写像

$\displaystyle \begin{align} \tilde{\varphi_0} \colon \;\;\;\; \tilde{U_0} \;\;\;\; &\longrightarrow \;\;\, \mathbb{C}, \\ (x_0, x_1) \;& \longmapsto \;\; \frac{x_1}{x_0} \end{align}$

を考えます。これは、 $\mathbb{C}^2$ の開集合上の有理式で表される関数です。分母 $x_0$ が $0$ にならないことから、これは連続関数を与えます。

商位相の普遍性より、 $\tilde{\varphi_0} \colon \tilde{U_0} \to \mathbb{C}$ が連続であることと、 $\varphi_0 \colon \pi( \tilde{U_0} ) \to \mathbb{C}$ が連続であることは同値です：

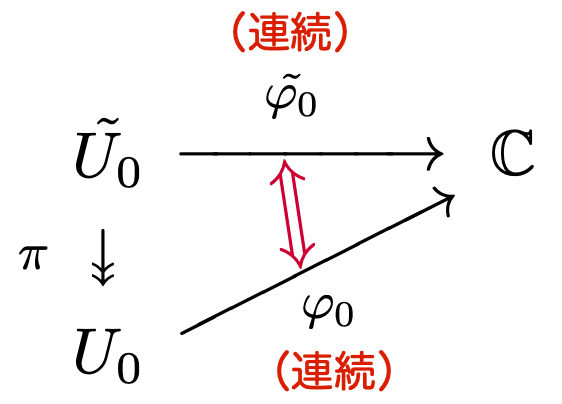
f:id:tsujimotter:20210308183340p:plain:w150

したがって、 $\varphi_0$ は連続であることが示されました。

φ₀⁻¹ の連続性

写像

$\displaystyle \begin{align} \tilde{\psi_0} \colon \;\; \mathbb{C} \; &\longrightarrow \;\; \tilde{U_0}, \\ y \;& \longmapsto \; (1, y) \end{align}$

を考えます。第1成分は $y \mapsto 1$ 、第2成分は $y\mapsto y$ です。 $\mathbb{C} \to \mathbb{C}$ の多項式写像は連続より、第1成分・第2成分ともに連続写像です。よって、直積位相の普遍性より $\tilde{\psi_0}$ は連続です。

また、 $\pi \colon \tilde{U_0} \to U_0$ との合成写像を考えると、 $\varphi_0^{-1} = \pi \circ \tilde{\psi_0}$ であり、合成写像の連続性より $\varphi_0^{-1}$ は連続です。

$\begin{eqnarray} \varphi_0^{-1}\colon\;\; & \mathbb{C} & \xrightarrow{\; \tilde{\psi_0} \;} & \;\; \tilde{U_0} & \xrightarrow{\pi} & \;\;\, U_0 \\ & y & \longmapsto & (1, y) & \longmapsto & [1 : y] \end{eqnarray}$

以上により、 $\varphi_0$ が同相写像であることが示されました。

2-3. 座標変換が正則関数

$U_0 \cap U_1 \neq \emptyset$ であることは明らかです。よって

$\varphi_{1}\circ \varphi^{-1}_{0}\colon \varphi_{0}(U_{0} \cap U_{1}) \to \varphi_{1}(U_{0} \cap U_{1})$

は正則関数であることを示しましょう。

f:id:tsujimotter:20210308140739j:plain:w340

$\varphi_0, \varphi_1$ の定義から、具体的には次の合成写像であることがわかります：

$\begin{eqnarray} \varphi_{1}\circ \varphi^{-1}_{0} \colon \;\; & \mathbb{C}\setminus \{0\} & \longrightarrow &U_0\cap U_1& \longrightarrow & \mathbb{C}\setminus \{0\}, \\ & x & \longmapsto & \; [ 1 : x] & \longmapsto &\;\;\; \frac{1}{x}\end{eqnarray}$

よって、 $\varphi_{1}\circ \varphi^{-1}_{0}(x) = \frac{1}{x}$ は $\mathbb{C}\setminus \{0\}$ 上の正則関数であることがわかります。

$U_0$ と $U_1$ の立場を入れ替えて、同様に示すことができます。

2-4. 正則行列によって表せる ℙ¹ から ℙ¹ への同相写像

（この節の議論は、後でハウスドルフ性を示すための準備です。）
$A = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{GL}(2, \mathbb{C})$ とします。すなわち、 $A$ は逆行列を持つ（行列式が0ではない）複素係数の2次正方行列です。

このとき

$\begin{align} p_A \colon\;\;\;\; \mathbb{P}^1\;\;\; &\longrightarrow \;\;\;\;\mathbb{P}^1, \\ [x_0 : x_1] &\longmapsto [ax_0 + bx_1 : \; cx_0 + dx_1] \end{align}$

で表される写像 $p_A$ を考えると、 $p_A$ は $\mathbb{P}^1$ から $\mathbb{P}^1$ への同相写像であることを示します。

あたかも、ベクトル $(x_0, x_1)$ に行列 $A$ を掛けるように、 $\mathbb{P}^1$ 上の同相写像が得られます。

まず、 $p_A$ がwell-definedであることを示します。

行列 $A$ を $\mathbb{C}^2$ に作用させると

$\begin{align} A \colon \;\;\;\; \mathbb{C}^2\;\; &\longrightarrow \;\;\;\;\mathbb{C}^2, \\ (x_0, x_1) &\longmapsto (ax_0 + bx_1, \; cx_0 + dx_1) \end{align}$

なる線形写像が得られます。

$A(0, 0) = (0, 0)$ より、 $A$ を $\mathbb{C}^2 \setminus \{(0, 0)\}$ に制限させた写像は

$\begin{align} A \colon \mathbb{C}^2 \setminus \{(0, 0)\} &\longrightarrow \;\;\;\;\mathbb{C}^2 \setminus \{(0, 0)\}, \\ (x_0, x_1) \;\;\;&\longmapsto (ax_0 + bx_1, \; cx_0 + dx_1) \end{align}$

となります。

$\mathbf{x} \in \mathbb{C}^2 \setminus \{(0, 0)\}$ および $c \in \mathbb{C} \setminus \{0\}$ に対し

$A(c\mathbf{x}) = cA(\mathbf{x})$

が成り立つので

$\pi( A(c\mathbf{x}) ) = \pi( A(\mathbf{x}) )$

が得られますが、これは $p_A := \pi \circ A \circ \pi^{-1}$ が $\mathbb{P}^1$ 上の写像としてwell-definedに定まることを意味します。

ここで、 $A$ と $\pi \colon \mathbb{C}^2 \setminus \{(0, 0)\} \to \mathbb{P}^1$ の可換性を考えると、次の可換図式が成り立ちます：

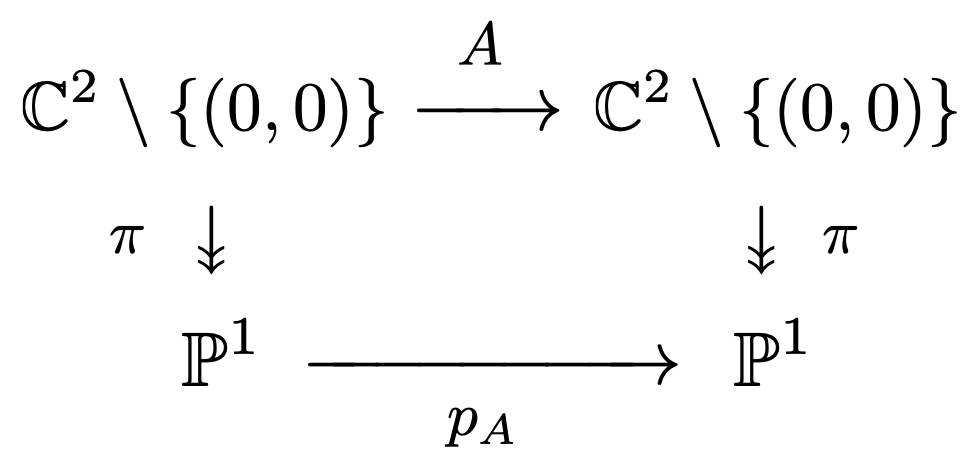
f:id:tsujimotter:20210308033428p:plain:w240

ここで対角線方向の写像を考えると、 $A$ と $\pi$ が連続より合成写像 $\pi \circ A$ は連続です。

f:id:tsujimotter:20210308142021p:plain:w240

また、 $p_A \circ \pi = \pi \circ A$ は連続であるから、商位相の普遍性より $p_A$ も連続であることがわかります。

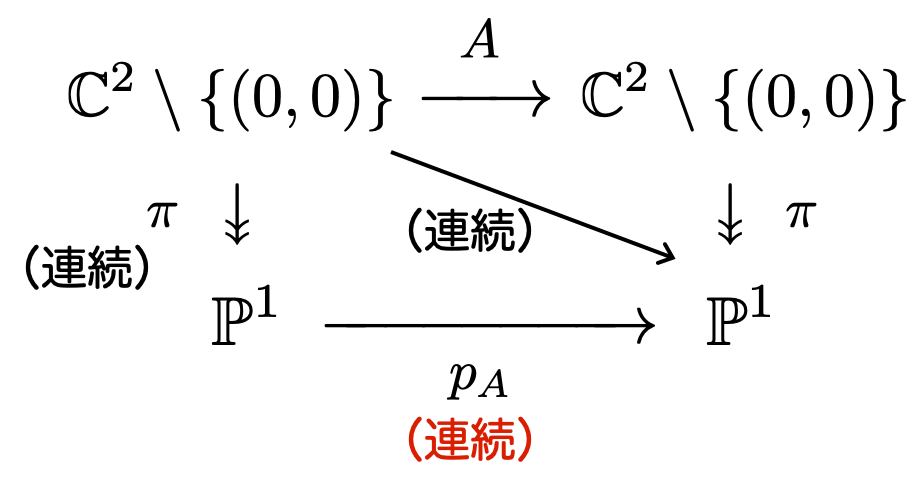
f:id:tsujimotter:20210308142111p:plain:w240

よって、 $p_A \colon \mathbb{P}^1 \to \mathbb{P}^1$ が連続であることが示されました。

また、 $A$ が逆行列 $A^{-1}$ を持つことから $p_A$ が全単射であることは明らかです。 $p_A^{-1} = p_{A^{-1}}$ より、 $A^{-1}$ に対して同様の議論を行うことで、 $p_A^{-1}$ が連続であることもわかります。

よって、 $p_A$ が同相写像であることが示されました。

2-5. ℙ¹ は第2可算公理を満たす連結かつコンパクトなハウスドルフ空間

ℙ¹ は第2可算公理を満たす

$\mathbb{C}$ の部分集合 $\mathbb{Q}(i)$ の点を中心とする半径有理数の開球を考えると、これが $\mathbb{C}$ の開基を与えます。これらの開基は可算個なので、 $\mathbb{C}$ は第2可算公理を満たします。

さらに、 $\mathbb{P}^1$ は $U_0$ と $U_1$ の合併であり、また $U_0$ と $U_1$ は $\mathbb{C}$ と同相です。よって、 $\mathbb{P}^1$ は第2可算公理を満たすことが示されました。

ℙ¹ は連結かつコンパクト

$\mathbb{C}^2 \setminus \{(0, 0)\}$ の部分集合

$S^3 := \{(x_0, x_1) \in \mathbb{C}^2 \mid |x_0|^2 + |x_1|^2 = 1 \}$

を考えます。（ $\mathbb{C}^2 = \mathbb{R}^4$ だと思うと、これは4次元空間内の3次元球面を表します。）

これは連結であることがわかります。

$S^3$ は任意の2点を通る大円を考えることで弧状連結であるとわかります。「弧状連結ならば連結」より、 $S^3$ が連結であることが示されます。

また、有界閉集合であることもわかります。

有界であることは明らか。

$S_3 \to \mathbb{R}; (x_0, x_1) \mapsto |x_0|^2 + |x_1|^2 = 1$ なる写像を考えると、これは連続写像となります。よって、閉集合の逆像は閉集合になります。

一方、 $\mathbb{R}$ はハウスドルフより1点集合 $\{1\}$ は閉集合です。ゆえに、その逆像 $S^3$ は閉集合。

ここで、商写像 $\pi \colon \mathbb{C}^2 \setminus \{(0, 0)\} \to \mathbb{P}^1$ を $S^3$ に制限すると

$\pi|_{S^3} \colon \;\; S^3 \longrightarrow \mathbb{P}^1$

が得られます。これが全射連続写像であることを示します。

$[x_0 : x_1] \in \mathbb{P}^1$ に対して、 $\pi(x_0, x_1) = [x_0 : x_1]$ となりますが、一般に $(x_0, x_1) \in S^3$ とは限りません。一方で、 $[x_0 : x_1]$ の代表元として $[\frac{x_0}{\sqrt{|x_0|^2 + |x_1|^2}} : \frac{x_1}{\sqrt{|x_0|^2 + |x_1|^2}}]$ を取ることにすると、対応する $(\frac{x_0}{\sqrt{|x_0|^2 + |x_1|^2}}, \frac{x_1}{\sqrt{|x_0|^2 + |x_1|^2}})$ は $S^3$ の点になります。よって、 $\pi|_{S^3}$ は全射です。