2021-02-28

1000以下の素数は250個以下であることを示せ（一橋大学・2021年第1問）【※数学ジョーク記事です】

数学

一橋大学の問題が僕にも解けそうだったので、解いてみました！

問題（一橋大学・2021年第1問）

1000以下の素数は250個以下であることを示せ。

2021-02-23

「23」とフェルマーの最終定理

数学素数整数論クンマーおすすめの記事

本日は 2/23 ということで、この日付にまつわる楽しい数学の話をしたいと思います！

お話したいのは、23 という数そのものが持つ性質についてです。

f:id:tsujimotter:20210222234128p:plain:w400

$23$ は素数なので、素数についての話かと思った方もいるかもしれません。

もちろん、素数であることは大事なのですが、それだけではありません。 $23$ は次のような特徴を持つ素晴らしい数でもあるのです。

$p$ を3以上の素数としたとき、
$p$ 次円分体の類数が $1$ より大きくなる最小の $p$ は $23$ である

整数論を学んだ人にとっては、円分体や類数の意味が理解でき、そこから23の性質に感動を覚える人も少なくないかと思います。

一方で、円分体や類数をまったく知らない人にとっては、上の説明だけでは何のことかわかりませんよね。私自身、何度か一般向けの講演で上の事実を紹介したことがあるのですが、難しくて理解できなかったという方も多いのではないかと思います。

そんな方でも、今回こそは23の魅力について理解できるようになる、そんな解説を目指したいと思います。

円分体や類数といった概念は、実はフェルマーの最終定理という世紀の難問（現在は定理）と密接に結びついています。今日はこの関係について、できるだけわかりやすく解説することを目標にしたいと思います。

2/23という日に、今日の日付を、 $23$ という数を好きになってもらえたら嬉しいです！

2021-02-22

単連結ではない領域のド・ラームコホモロジー

数学解析学積分ド・ラームコホモロジー

こちらの記事の続きです。
tsujimotter.hatenablog.com

上の記事では、穴あき円板 $D_2$ 上のド・ラームコホモロジー $H^1(D_2, \mathbb{R})$ を計算しました。

$D_2 := \{ (x, y) \in \mathbb{R}^2 \mid 0 < x^2 + y^2 < 1 \} \tag{1}$

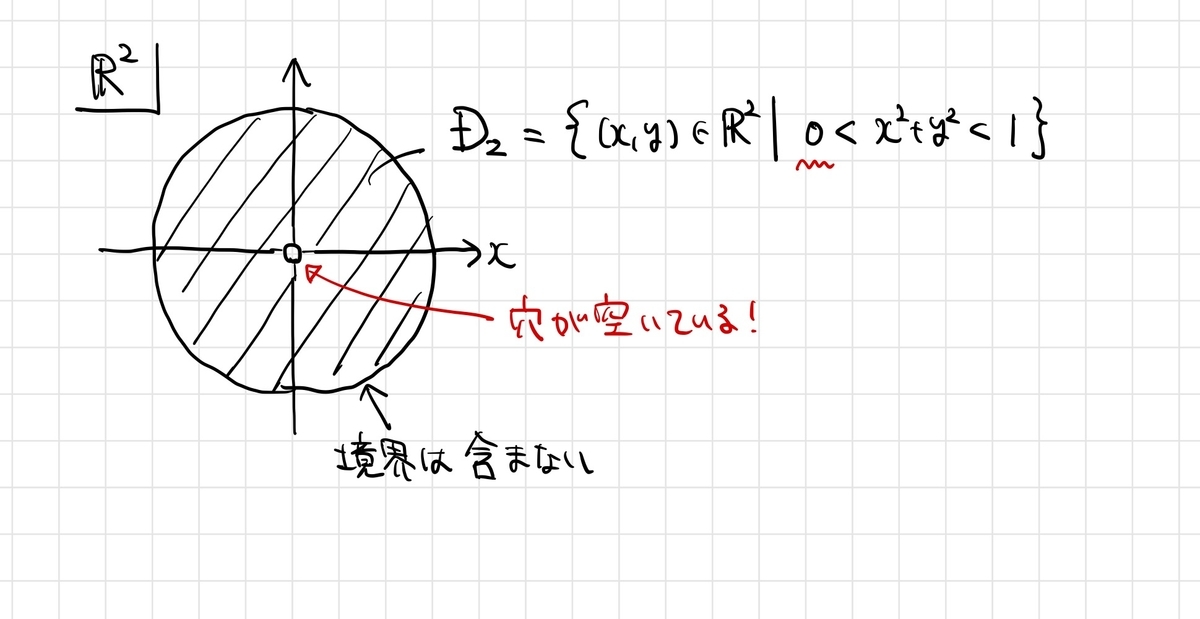
ド・ラームコホモロジーを計算するには、 $D_2$ 上の任意の閉1形式（ $Z^1_{\text{dR}}(D_2) := \operatorname{Ker}(d^1)$ の元）を計算し、それと完全1形式（ $B^1_{\text{dR}}(D_2) := \operatorname{Im}(d^0)$ の元）との「差」（実際は商ベクトル空間）を計算する必要があります。

このとき、非自明な元

$\displaystyle \omega_0 = \frac{-y}{x^2 + y^2}dx + \frac{x}{x^2 + y^2}dy \tag{2}$

が存在して、 $\omega_0$ が閉1形式でありながら完全1形式ではないことを示しました。

前回の記事では、「ド・ラームの定理」という非常に大きな定理を使うことで、 $H^1(D_2, \mathbb{R})$ の $\mathbb{R}$ 上の次元が1であることを示し、結果として $\omega_0$ が1次元の基底をなすことを示したのでした。

しかしながら、ド・ラームの定理を使うのはちょっと大掛かりすぎますね。もっと直接的に示す方法はないものかと思っていました。そんな折に、ラスクさん（ @washoi4150 ）という方からTwitterで「直接的に示す方法はあるよ」と教えていただけました。

そこで今回は、ラスクさんに許可をいただきまして、 $D_2$ 上のド・ラームコホモロジーのより直接的な計算方法を紹介したいと思います。

常々思っているのですが、ブログを書いて公開することによって、自分自身が一番勉強になっています。

タイムラインに僕より専門的な数学に詳しい人がたくさんいるので、記事に書くと「こんなのありますよ！」というのを教えてくださるのが嬉しい。

書けば書くほど僕自身が勉強になるポジティブフィードバックが出来ています。大変ありがたい話です。
— tsujimotter 日曜数学者 (@tsujimotter) 2021年2月18日

私自身は独学で数学を勉強しているので、本に書いてない内容についてはただただ自分の頭で考えるしかないのですが、どうしてもわからずに断念してしまうことが多々あります。なので、私の知らないアイデアをより詳しい人に提供いただけるのは、本当にありがたいことです。

独学で数学を勉強していて、私と同じように悩んでいる人はいるのかもしれません。私のケースがどれぐらい一般化できるのかは分かりませんが、「自分がここまで理解したぞ」という部分を、ブログなりSNSなりで（理解が完全でないことを承知の上で）アウトプットしてみるというのも悪くはないのではないかなと思っています。*1

今後もこういったコミュニケーションを大事にしながら、勉強を進めていきたいと思っています。

それでは内容に入っていきましょう！

*1:結城先生による質問回答の内容が大変共感できるものだったので、リンクを共有します。

質問（学んだことを発表したいが未熟をさらけ出すのが不安）

ご質問ありがとうございます。あなたが感じる不安はとてもよく理解できます。そしてその不安をどう扱うかは極めて重要です。(続く)#結城浩に聞いてみよう https://t.co/CXeXYzO7EF pic.twitter.com/1GwGgN6c4R
— 結城浩 / Hiroshi Yuki (@hyuki) 2021年2月17日

2021-02-20

ナッシュの定理の証明：有限ゲームの混合戦略にはナッシュ均衡点が存在する

数学ゲーム理論おすすめの記事

先日、予備校のノリで学ぶ「大学の数学・物理」さん（以下、ヨビノリさん）のYouTubeチャンネルにて、ゲーム理論に関する動画が公開されました。

www.youtube.com

ゲーム理論に関する基本的な用語について、大変わかりやすく紹介されているのでぜひご覧になってください。ゲーム理論において、重要な「解」概念である「ナッシュ均衡点」や「パレート効率」といった概念も紹介されていました。

さて、今回私の記事で紹介したいテーマは「ナッシュ均衡点の存在性」についてです。（混合戦略を考えない）純粋戦略のゲームにおいては、ナッシュ均衡点の存在しないゲームが存在します。具体的には、動画にも紹介された「じゃんけんゲーム」などがそうですね。

A＼B	グー	チョキ	パー
グー	$(0, 0)$	$(1, -1)$	$(-1, 1)$
チョキ	$(-1, 1)$	$(0, 0)$	$(1, -1)$
パー	$(1, -1)$	$(-1, 1)$	$(0, 0)$

一方で、（これもまた動画内で触れられていますが）混合戦略という、各プレーヤーが戦略を確率的に選ぶような状況にゲームを拡大すると、なんと必ずナッシュ均衡点が存在するということが知られています。

これは大変興味深い定理かと思います。

定理（ナッシュの定理）

有限個の戦略を持つ任意のゲームは、混合戦略の範囲でナッシュ均衡点を持つ。

もちろん、ナッシュ自身が「ナッシュ均衡点」と呼んだわけではありません。ナッシュがこの定理を示したからナッシュ均衡点という名前がついたわけですね。そして今やゲーム理論における超重要概念になっています。

tsujimotterは、三年ぐらい前からこの定理の証明をブログに書きたいと思っていました。しかしながら、ゲーム理論の基本的な設定を説明するのが面倒で、断念しておりました。ヨビノリさんの動画をみて、これはすばらしい、ぜひ乗っからせていただこう！と思ったのが執筆の経緯です。笑

ヨビノリさんの素晴らしい動画に感謝しつつ、証明を紹介させていただきます。

なお「ナッシュの定理」の証明には、不動点定理という定理が使われていまして、その定理の使いどころが今回の記事の一番のポイントになります。不動点定理自体の証明について今回はやりませんが、いったいどうやってナッシュ均衡点の存在を導くのかという点に着目して楽しんで頂ければと思います。

元々はヨビノリさんの動画からシームレスにつながるようなレベル感の記事にしようと思っていたのですが、どうもそれは難しそうです。内容が単純に難しいのです・・・。というわけで、それなりに数式も多くなってしまいますが、数学（特に集合と写像）にある程度慣れている人には読めるものにはなっているかと思います。

以前からゲーム理論を知っていた方でも、（ナッシュの定理の）証明は知らないという方も多いのではないでしょうか。有名な定理なので、一度はその証明に触れてみたいですよね。これを機にぜひ味わっていただきたいと思います。

最後まで通して読むのにはなかなか時間がかかると思いますので、読んでいる途中でも構いませんので

「（途中までしか読んでないけど）面白い！」とか
「ナッシュやばい！！」とか
「ベイマックスwww」とか

呟いていただけると嬉しいです。

それでは、じっくりお楽しみください！

2021-02-19

完全微分方程式とド・ラームコホモロジー

数学解析学積分ド・ラームコホモロジー

微分方程式には色々な種類があって、それぞれ解き方が異なったり、そもそも解けなかったりします。

理系大学生であれば大学１・２年でさまざまな微分方程式の解き方を習うわけですが、これは微分方程式の中でもほんの一部である「うまく解ける微分方程式」の解き方を学んでいるにすぎません。タイトルにある完全微分方程式は、そのような常微分方程式の一種です。

$P(x, y), \;\; Q(x, y)$ を $C^1$ 級（1階偏微分可能かつ1階偏導関数が連続な）2変数実関数とします。このとき

$P(x, y) dx + Q(x, y) dy = 0 \tag{1}$

の形の微分方程式を考えます。

加えて完全微分形という条件を考えます。この条件を満たすかどうかで、式 $(1)$ の微分方程式の解き方が変わります：

（完全微分形） $(x, y) \in \mathbb{R}^2$ に対して $\displaystyle \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}$ が成り立つ

微分方程式 $(1)$ が完全微分形の条件を満たすとき、完全微分方程式といいます。
（満たさない場合は「不完全微分方程式」といって、取り扱いが異なってきます。こちらについては今回は扱いません。）

完全微分形の条件を満たすとき、次が成り立つことが知られています：

ある $C^1$ 級関数 $f(x, y)$ が存在して

$df = P(x, y) dx + Q(x, y) dy$

が成り立つ。

また、このように書けるのは完全微分形のときに限られることもわかります。すなわち、式 $(1)$ が完全微分形であるための必要十分条件というわけですね。この事実は超重要なので、次節で証明したいと思います。

実際、完全微分形の条件を満たすとき $df = P dx + Q dy$ であり、また式 $(1)$ から $P dx + Q dy = 0$ なので、合わせて

$df = 0$

が言えます。よって、定数 $c \in \mathbb{R}$ を用いて

$f(x, y) = c$

が言えることになります。これは、元々の完全微分方程式 $(1)$ を満たす $(x, y)$ の組を陰関数によって表現した方程式になっており、これが微分方程式の解と言えるわけです。

これが完全微分方程式 $(1)$ の解法だったわけでした。

ここからが今日の本題です。完全微分方程式を解くために必要であった条件は、まさに $\mathbb{R}^2$ 上のド・ラームコホモロジーを計算する際に必要な条件そのものであった、というのが今日話したい内容です。すなわち、完全微分形の必要十分条件は

閉1形式　 $\Longleftrightarrow$ 　完全1形式

を表しているのです。

今回の記事では、前半で完全微分方程式の必要十分条件の証明を行います。後半では、この条件がまさに、ド・ラームコホモロジーにおける条件を表していることを具体的な例を元に説明したいと思います。

2021-02-18

2変数2次関数の極値問題（平方完成と主軸変換の図形的な意味）

数学解析学幾何学

前回の記事の続きです（前回の記事を読まなくても、今回の内容は読むことができます）：
tsujimotter.hatenablog.com

前回の内容を簡単に振り返ります。「空間内の与えられた2直線 $l_1, l_2$ に対して、その距離を求めることはできるか？」という問題について考えました。 $l_1, l_2$ からそれぞれ点 $P, Q$ をとったとき、 $P, Q$ の距離は2変数の2次関数関数 $F(x, y)$ として求められます。 $F(x, y)$ の最小値を求めれば、 $l_1, l_2$ の距離が求まるという話でした。

ここで「2変数の2次関数の最小値はあるのか？」という部分が一つの焦点だったわけですが、 $l_1, l_2$ が平行でない場合には最小値が極小値に一致する（最小値は存在する）という結論でした。

上の記事では、 $F(x, y)$ を力技で平方完成して最小値を出していました。ところが、ブログ公開後にTwitter上で @Freufirst さんという方から「2次関数の平方完成は合同変換で出来るよ」という旨のアドバイスをいただきました。教えていただいた方法は「まさに」という方法だったのですが、昨日の時点ではまったく頭にありませんでした。ありがとうございます。

というわけで、せっかくなので行列を使った2変数2次関数の極値問題の解法について、詳しくまとめてみたいと思います。2変数2次関数 $F(x, y)$ が極小値（あるいは極大値など）を持つ条件について考察していきたいと思います。

今回は、行列やベクトルとしての式変形を用いてスマートに求めることを目指します。計算の途中では、いくつかの「行列やベクトルの変換操作」を行っていきますが、それらは単なる機械的な置き換えではなく、実はちゃんと図形的な意味があるものになっています。記事の後半では、そのことについても触れていきたいと思います。

2021-02-17

空間内の「ねじれの位置」にある2直線間の距離

数学幾何学

高校数学で習う「空間内の2直線間の距離」について考えてみたいと思います。

3次元空間内に2直線 $l_1, l_2$ があるとします。 $l_1, l_2$ が「ねじれの位置にある」とは、 $l_1, l_2$ が交点を持たず、かつ、平行でもないことを言います。このとき、2直線 $l_1, l_2$ の距離を考えてみたいと思います。

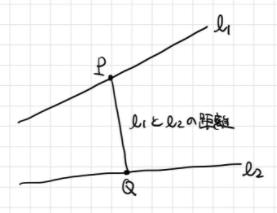
そもそも2直線の距離とは、というところから考えたいと思います。 $l_1$ の点 $P$ および $l_2$ の点 $Q$ を任意にとったとき、距離 $PQ$ の最小値を2直線 $l_1, l_2$ の距離と定義します。

ここで疑問に思うのは、そもそもこの最小値は存在するのか？、という問題です。2直線の位置関係によっては、2直線のそれぞれの点の距離がいつまでも漸近的に小さくなり続けるなんてこともあるかもしれません。この場合、最小値は存在しないことになります。もちろん、直感的にはそんな状況はなさそうに思えますが、証明される必要があると思います。

最小値が存在しなければ、2直線の距離は定義できない場合が存在するということになってしまいますね。

この記事の最後に述べるように、結果的には最小値は存在し、2直線の距離が定義できます。この事実って高校数学では証明されるのでしょうか？　少なくともtsujimotterはこの証明について聞いた記憶がありませんでした。証明が気になって眠れません。

というわけで、最小値が存在することについて自分なりに考えてみたのがこちらの記事となります。今回は「ベクトル解析」を使った証明ですが、もしかしたら、もっと簡単に考えることもできるかもしれません。

個人的に楽しかったのでまとめてみたという記事になりますので、おおらかな目でみてあげてください。別解などあればお気軽におしらせください。

（追記）
実は最後に書いたのですが、もっとシンプルな解決策があったようです。結果的には、前半で書いたような計算はしなくてもよかったのですが、計算していて楽しかったのでそのまま載せたいと思います。