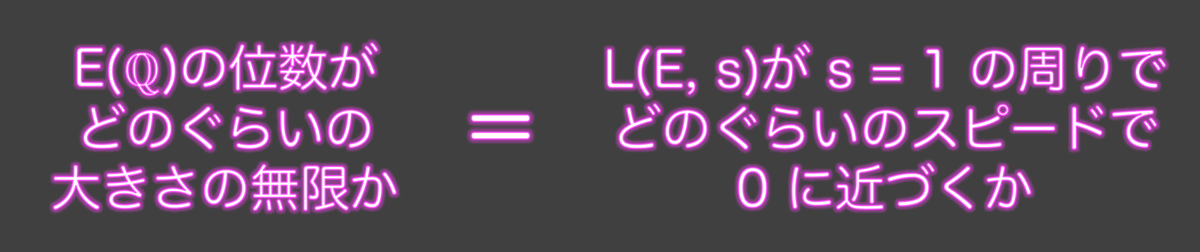2020-09-23

ベータ関数とフェルマー曲線の周期

数学リーマン面代数幾何積分

前回書いた積分の記事が大変話題になりまして嬉しいです。
tsujimotter.hatenablog.com

今日も積分についての話を書いてみたいと思います。

定積分によって定義される特殊関数、ベータ関数

$\displaystyle \operatorname{B}(p, q) = \int_{0}^{1} t^{p-1}(1-t)^{q-1} dt \tag{1}$

について紹介しましょう。

有名な特殊関数なので、ベータ関数自体は知っている方は多いかと思います。

前回の記事では、 $\int \frac{1}{\sqrt{x^2 + 1}}dx$ という積分が、双曲線 $y^2 - x^2 = 1$ 上の積分だという話をしました。

実は今回の積分にも、フェルマー曲線という曲線が背景にあります。そんな面白そうな話を紹介してみたいと思います。

目次：

1. フェルマー曲線

2. ベータ関数の変形

3. コンパクトリーマン面と周期の定義

4. フェルマー曲線上の周期

参考記事

2020-09-14

無理関数の不定積分と双曲線、微分形式

数学自由研究・独自研究代数幾何積分

今日考えたいのは、

$\displaystyle \int \frac{1}{\sqrt{x^2 + 1}} dx$ 　や　 $\displaystyle \int \sqrt{x^2 + 1}\, dx$

というタイプの積分です。

いわゆる無理関数の積分と呼ばれるもので、大学受験でも難関大学の問題として登場するみたいですね。

今回の記事のきっかけとなったのは、清さんによる以下のツイートです：

【清史弘からの提案 7 】
　教育系YouTuber の人に向けて、このような動画はどうですか? という内容です。もちろん、YouTuber でない方もご参加ください。
　私の考え方は24時間以内にあげようと思っています。
　これは、唯一の正解というよりは、いろいろとあってよいと思います。#清史弘からの提案 pic.twitter.com/UokREtslQt
— 清　史弘 (@f_sei) 2020年9月13日

上のツイートによると、今回の積分は

$t = x + \sqrt{x^2 + 1} \tag{1}$

という変数変換がキーになるようですが、いったいどこからこの式が現れたのか説明せよ、というのが問題です。

清さんのツイートの引用リツイートに、加藤文元先生がこんな意味深なツイートを残されています：

大学教科書ですが、これ私の教科書には書きました（数研講座大学教養微分積分 p.146）。代数関数の積分が有理関数の積分に帰着できるか否かには、代数曲線論による少し深い背景があるという話ですが、逆に言えば、どういうときにはそういう変数変換が不可能かということもわかります。 https://t.co/pw4Ap7taX3
— Fumiharu Kato 加藤文元（Bungen） (@FumiharuKato) 2020年9月13日

どうもこの積分には深い数学的背景があるようです。このツイートを見てtsujimotterは面白そうだと思いました。

実際、代数曲線論に基づく議論によって、上記の変数変換で積分が解けることを説明できそうです。このことについてまとめてみようとおもいます。

清さんの元々の問題は受験生を対象とした説明を想定されていて、私が理解した内容はそれを大きく超えてしまっています。

したがって、今回の記事の内容は 受験生の役に立つものではありません。上の問題の答えというわけでもありません。それでも面白そうなので、せっかくだからまとめてみようというのが本記事の趣旨です。よろしければご覧いただければ幸いです。

また、今回の内容は、特にどこかに書いてあった話というわけではなく、私が今まで見聞きした情報を元に「多分こうだろう」と思って書いた内容になります。内容の正確性は保証できませんので、その点ご了承いただければと思います。

2020-09-08

ミレニアム問題「BSD予想」の主張を1から理解したい！（ざっくり編）

数学楕円曲線おすすめの記事

ミレニアム問題という言葉を聞いたことがあるでしょうか？

アメリカのクレイ研究所という数学の研究所によって2000年に発表された、数学における7つの未解決問題のことです。21世紀に解かれるべき重要な問題がリストアップされており、それぞれに 100万ドルの懸賞金が掛けられたことで知られています。

有名なものだとリーマン予想やポアンカレ予想があります。ポアンカレ予想だけは2003年に解決されていて、解決の際に大変話題になったのを覚えている人も多いかと思います。

ミレニアム問題の一覧をリストアップしてみましょう：

ヤン–ミルズ方程式と質量ギャップ問題
リーマン予想
P≠NP予想
ナビエ–ストークス方程式の解の存在と滑らかさ-
ホッジ予想
ポアンカレ予想
バーチ-スウィンナートン・ダイアー予想

今回紹介したいのは、リストの最後に挙げた

バーチ-スウィンナートン・ダイアー予想

です。

バーチ-スウィンナートン・ダイアー予想は、バーチとスウィンナートン・ダイアーという２人の数学者によって提唱された予想で、名前の頭文字をとって BSD予想と呼ばれます。今回の記事でも以降BSD予想と呼ぶことにします。

（注）よく誤解されますが、予想を提唱したのは２人です。名前の繋がり的に３人に見えますが、２人です。

みなさんはこのBSD予想についてどのくらいご存知でしょうか？

ミレニアム問題に興味を持ち、一度くらいはBSD予想について調べてみようと思ったことがあるのではないでしょうか。そして、Wikipediaで検索してみてもよく分からなかった、「楕円曲線」「ランク」「L関数」と色々な用語が出てきて何のこっちゃ分からなかった、そんな方も多いのではないかと思います。この記事はそんなあなたのための記事です。

BSD予想はそもそも主張を理解するためだけであっても一定の専門知識が求められるため、ミレニアム問題の中では知名度が低いかもしれません。一方で、私個人の主観に基づく評価ですが、BSD予想はミレニアム問題の中で一番面白い予想だと思います。こんなに面白いのに知られていないのはもったいないと思っています。

そんなBSD予想の主張を紹介し、どんな風に面白いのかを説明して、読者の皆様にその魅力を感じてもらいたい、というのが今回の記事の趣旨です。

今回の記事は「ざっくり編」です

BSD予想の主張を理解するにあたって、本来であればさまざまな前提知識が必要になります。これらの前提知識はなかなか専門的なものですので、正確な定義を理解するためにはそれなりの時間が必要です。

しかしながら、BSD予想の主張をなんとなく感じとりたいという目的であれば、厳密な定義を避けて直感的な説明をすることは十分に可能だと思います。

今回の記事は、まさにそのような試みとなっています。あくまで直感的な理解を目指して、楕円曲線やBSD予想の主張について、ざっくりと解説したいと思います。題して

ミレニアム問題「BSD予想」の主張を1から理解したい！
（ざっくり編）

です。　

より詳しく知りたい方のために『詳細編』も用意していますので、この記事を読んだ後には、ぜひそちらにもアクセスしてみてください。
（本記事の最後に『詳細編』の紹介とリンクが掲載されています。）

BSD予想とは

BSD予想における登場人物は

「楕円曲線」と「（楕円曲線に付随する）L関数」

です。BSD予想は、これら２つの数学的対象の間の関係についての予想です。

まず、楕円曲線について紹介します。

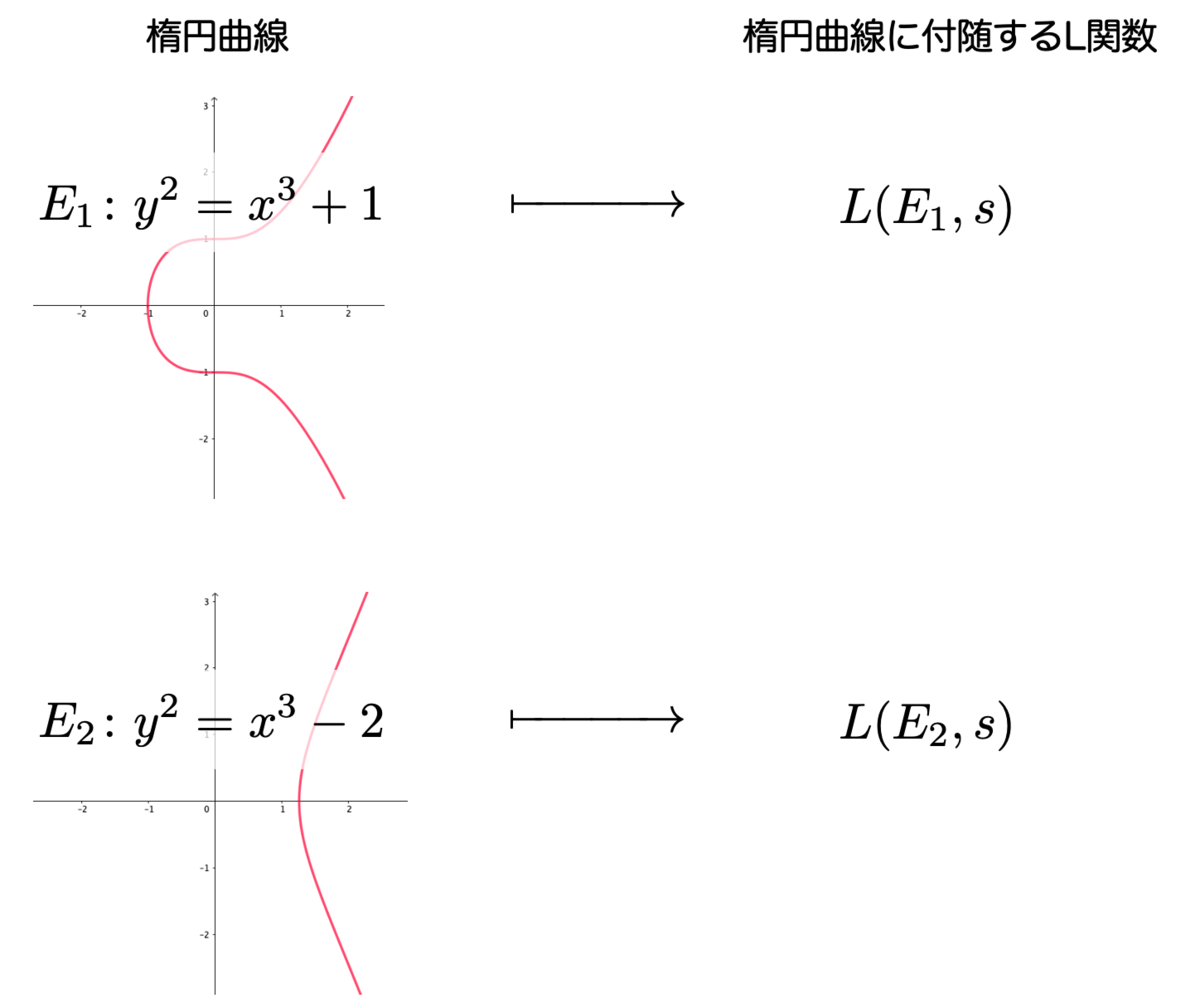
たとえば

$E_1\colon y^2 = x^3 + 1 \tag{1}$

$E_2\colon y^2 = x^3 - 2 \tag{2}$

というような曲線が楕円曲線です。これらの曲線の名前は、楕円曲線（Elliptic curve）の頭文字をとって、それぞれ $E_1, E_2$ と呼ぶしましょう。

左辺が $y$ についての2次式、右辺が $x$ についての3次式になっているのがポイントです。このような方程式で定義された曲線を一般に楕円曲線といいます。

楕円曲線は高校までの数学では扱われないような曲線です。高校までに扱った曲線は

$y = ax, \;\; y = x^2, \;\; x^2 + y^2 = 1, \;\; 2x^2 + 3y^2 = 1, \;\; x^2 - y^2 = 1$

というような曲線でした。それぞれ、直線・放物線・円・楕円・双曲線で、どの曲線についても $x, y$ の次数が高々 $2$ 次であるような曲線でした。

楕円曲線は、 $3$ 次の項が含まれる分、上記の曲線よりも「ちょっとだけ複雑な曲線」だといえます。

なお「楕円曲線」は「楕円」ではないことに注意しましょう。

イメージが大事だと思いますので、楕円曲線 $E_1, E_2$ を図示してみましょう。こんな感じの図形です。

f:id:tsujimotter:20200825221839p:plain:w420

楕円曲線は図のように「連続的な曲線」ですが、ここでは特に $x$ 座標と $y$ 座標がどちらも有理数になるような点を考えます。方程式でいうなら、式 $(1)$ の有理数解といっても良いでしょう。

このような点を楕円曲線 $E_1$ の有理点（あるいは $E_2$ の有理点）といいます。 $E_1$ の有理点全体の集合を $E_1(\mathbb{Q})$ 、 $E_2$ の有理点全体の集合を $E_2(\mathbb{Q})$ と呼ぶことにしたいと思います。

この $E_1(\mathbb{Q})$ と $E_2(\mathbb{Q})$ 、あるいは、一般の楕円曲線 $E$ に対する $E(\mathbb{Q})$ について、こんな問いを投げかけてみましょう：

$E_1(\mathbb{Q}), E_2(\mathbb{Q})$ の要素はいったいどれぐらいあるでしょうか？　有限個でしょうか、無限個でしょうか？

実は、 $E_1$ の場合は $E_1(\mathbb{Q})$ の要素数は有限個になり、 $E_2$ の場合は $E_2(\mathbb{Q})$ の要素は無限個になります。

楕円曲線によって異なるというのが答えです。有限個の場合もあるし、無限個の場合もあります。

BSD予想は、まさにこの $E(\mathbb{Q})$ が無限か有限かという問題に、一つの答えを与えてくれる予想となっています。

つづいて、もう一方の登場人物である L関数について紹介しましょう。

楕円曲線 $E$ に対し、 $L(E, s)$ という関数が定まります。 $L(E, s)$ は楕円曲線 $E$ に付随するL関数と呼ばれます。

L関数というのは、このブログにもよく登場するリーマンのゼータ関数

$\displaystyle \zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s} \tag{3}$

のちょうど親戚にあたるような関数です。

リーマンのゼータ関数は式 $(3)$ の関数が唯一ですが、L関数はたくさんあり、楕円曲線１つに対してL関数が１つ定まります。

f:id:tsujimotter:20200825235200p:plain:w420

$L(E, s)$ は、楕円曲線 $E$ の情報を使って作られる関数です。具体的な仕組みについては後ほど少しだけ説明をします。変数 $s$ は、リーマンのゼータ関数と同じように複素数の範囲を動きます。

BSD予想では、この関数の特に $s = 1$ における値に注目します。

リーマンゼータ関数 $\zeta(s)$ は、 $s = 1$ のときに無限大に発散しました。一方の $L(E, s)$ は $s = 1$ で値を持ちます。

今さらっと事実を述べましたが、この事実の背景にはとても興味深い理屈があるのです。これについては、少しもったいぶらせてください。「詳細編」で述べることにしたいと思います。

$s = 1$ の値に注目して $E_1, E_2$ に付随するL関数 $L(E_1, s), \; L(E_2, s)$ を観察してみましょう。

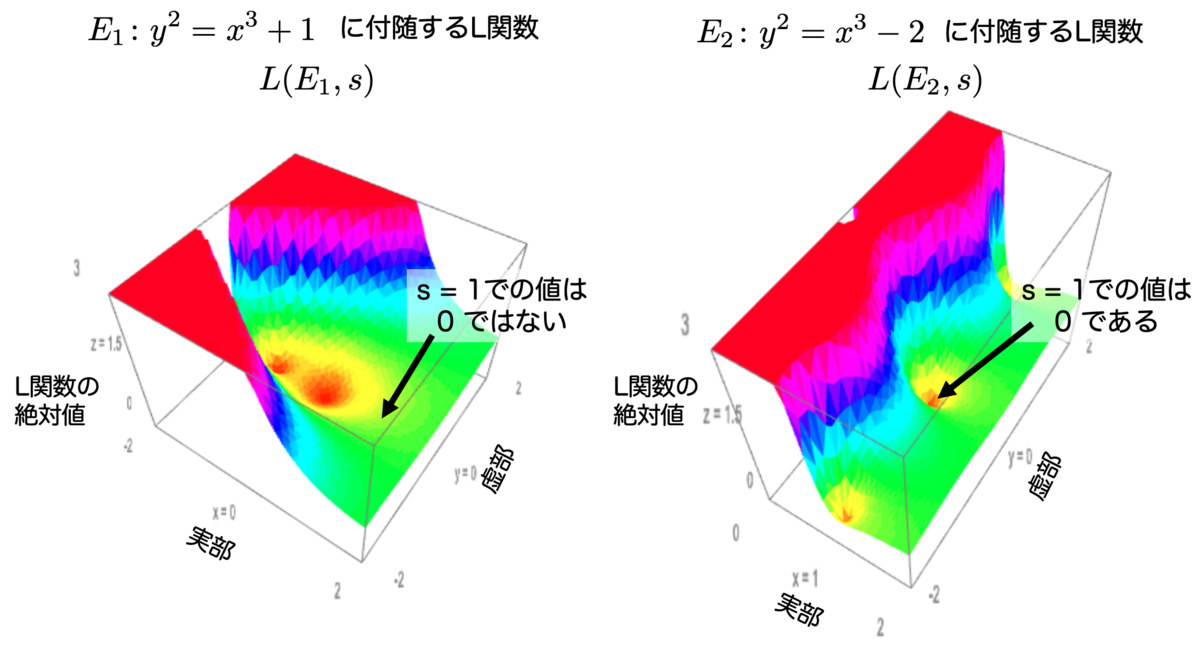
Sagemathというシステムを使って、L関数の値を計算しました。 $s$ の実部と虚部に対して、L関数の絶対値 $|L(E, s)|$ をプロットしたのが次の図になります：

f:id:tsujimotter:20200826004209p:plain:w500

図の「凹んでいる赤色の点」の周辺が、L関数の値が $0$ になる点です。その点に着目して観察すると、 $E_1$ の方は $L(E_1, 1) \neq 0$ であるのに対し、 $E_2$ の方は $L(E_2, 1) = 0$ となっています。一方で、 $E_1(\mathbb{Q})$ が有限個で、 $E_2(\mathbb{Q})$ が無限個であったことを思い出しましょう。

実際、次が成り立つことが予想されています：

$E(\mathbb{Q})$ の個数が有限個 $\;\; \Longleftrightarrow \;\; L(E, 1) \neq 0\tag{4}$

また同値な予想として

$E(\mathbb{Q})$ の個数が無限個 $\;\; \Longleftrightarrow \;\; L(E, 1) = 0 \tag{5}$

これらがまさに BSD予想の主張（の一部）です。

BSD予想は、楕円曲線 $E$ の有理点の個数が無限かどうかは、 $L(E, 1)$ が教えてくれるという予想だと言えます。我々が知りたかった楕円曲線 $E$ の有理点の個数の情報が、 $L(E, 1)$ を見ればわかるというのです。

正確にいうと、上記で述べた予想はBSD予想そのものではなく、BSD予想の主張の一部です。

実際のBSD予想は、これよりもう少し精密なものになっています。上記の予想は「有理点の個数が有限個か無限個か」についてのものでしたが、BSD予想ではそれ以上の情報が分かるというのです。

BSD予想の本来の主張を標語的に表すと、次のように表現できるでしょう：

f:id:tsujimotter:20200825233741p:plain:w480

正確な主張は次のものです。より踏み込んだ説明が必要なので「詳細編」でじっくりすることにしましょう。

BSD予想

$E$ を $\mathbb{Q}$ 上の楕円曲線とする。 $E(\mathbb{Q})$ を $E$ の $\mathbb{Q}$ -有理点のなす群とし、 $L(E, s)$ を $E$ に付随するL関数とすると、次が成り立つ：

$\displaystyle \operatorname{rank}_{\mathbb{Z}} E(\mathbb{Q}) = \operatorname{ord}_{s = 1} L(E, s) \tag{6}$

ただし、 $\operatorname{rank}_{\mathbb{Z}}$ は $\mathbb{Z}$ 上のランク（階数）を表し、 $\operatorname{ord}_{s = 1}$ は $s = 1$ における零点の位数を表す。

BSD予想の魅力

最後にBSD予想について、私の思う魅力について3つ述べたいと思います。

1つ目は、数学的な深さです。

ここまで読んできた読者の中には、こんな風な疑問を持った方もいるのではないでしょうか。

$L(E, s)$ は元々楕円曲線 $E$ の情報を使って定義されているのだから、 $L(E, s)$ が $E$ についての情報を持っていたとしても不思議ではないのでは。

きわめて自然な疑問だと思いますが、 $L(E, s)$ の定義に踏み込んで考えれば、そう単純な話ではないとわかります。

$L(E, s)$ は、楕円曲線 $E$ の方程式を「素数 $p$ で割ったあまり」で考えたときの情報によって定義されます。つまり $E\colon y^2 = x^3 + 1$ であれば

$y^2 \equiv x^3 + 1\pmod{2}$

$y^2 \equiv x^3 + 1\pmod{3}$

$y^2 \equiv x^3 + 1\pmod{5}$

$y^2 \equiv x^3 + 1\pmod{7}$

$\vdots$

という合同式を考えます。方程式の「 $\bmod{p}$ での解の個数」を $N_p$ としたとき、 $N_2, N_3, N_5, N_7, \ldots$ を使って $L(E, s)$ が定義されるのです。

実際、 $L(E, s)$ はこんな風に定義されます：

$\begin{align} \displaystyle L(E, s) := &\frac{1}{1 - (2+1-N_2)\frac{1}{2^s} + \frac{1}{2^{2s-1}}} \times \frac{1}{1 - (3+1-N_3)\frac{1}{3^s} + \frac{1}{3^{2s-1}}} \\ &\times \frac{1}{1 - (5+1-N_5)\frac{1}{5^s} + \frac{1}{5^{2s-1}}} \times \frac{1}{1 - (7+1-N_7)\frac{1}{7^s} + \frac{1}{7^{2s-1}}} \times \cdots \end{align} \tag{7}$

$L(E, s)$ の定義はかなり複雑に見えますが（実際かなり複雑ですが）、そこには $E$ の有理点についての情報は使われていません。一見すると、有理点とはまったく関係ないように見えます。

これらの情報がなぜか結びついてしまうというのが、BSD予想の不思議なところなのです。

一見関係ないように見える二つの対象が、結びついてしまうというのは、その背景にきっと深い理由があるはずです。BSD予想のような現象は、あくまで表面的に見えている氷山の一角なのだと思います。本当はもっと深い数学的な関係が隠れているはずで、見え隠れする数学の世界の深遠に私はワクワクします。

2つめは、発見の経緯の面白さです。

BSD予想がコンピュータによる計算によって予想されたというのも、なかなか興味深いエピソードだと思います。

BSD予想が提唱されたのは、1960年代初頭です。当時、コンピュータと呼ばれるものが登場したばかりでした。スウィンナートン・ダイアーは、EDSAC*1の後継機であるEDSAC 2を使って式 $(7)$ の計算をし、BSD予想に至ったそうです。

この辺の計算も、現在のパソコンを使って実際にトレースすることができます。計算して楽しむことができるというのも面白いです。「詳細編」では、この具体的な計算もやってみたいと思います。

3つめは、これは個人的な理由ではありますが、解決のための手法の面白さです。

BSD予想は未解決問題ですが、実は予想の一部分については既に解決しているのです。最初のブレイクスルーは、コーツとワイルズという数学者によるものなのですが、その論文では $\mathbb{Z}_p$ 拡大という岩澤理論的な発想が用いられています。

岩澤理論は、まさに私がこれまで追いかけてきた「お気に入りの」理論だったので、この事実を知ってBSD予想にとても興味が湧いてきました。BSD予想の研究はコーツ-ワイルズよりさらに進んでいるようで、それらの研究においても岩澤理論的な手法は使われているようなのです。BSD予想はどこまで解決したのか、そして部分的解決の糸口となった手法はいったいどのようなものなのか。これらについても掘り下げて理解できたらと思っています。

コーツ-ワイルズの論文については、以前の記事で（かなり難しい内容ではありますが）その概要をまとめたことがあります：
tsujimotter.hatenablog.com

色々紹介してきましたが、BSD予想の魅力は伝わりましたでしょうか？

もちろん、今回紹介したことはあくまで表面的なものです。BSD予想の面白さをより深く実感するには、今回ざっくり説明した話を、より詳しく・正確に理解する必要があります：

楕円曲線とは
有理点とランクとは
楕円曲線に付随するL関数とは
BSD予想の正しい主張とは

「ミレニアム問題「BSD予想」の主張を1から理解したい！（詳細編）」では、上記について1からじっくりと説明したいと思っています。その上で次のような「もう少し踏み込んだ解説」をできればと思っています：

BSD予想はどうやって予想されたのか
BSD予想はどこまで解決されたのか

楕円曲線やBSD予想について、もっと詳しく知りたいという方はぜひご覧になってください。

ここまで読んでくださりありがとうございました！

それでは、今日はこの辺で！

続きが知りたくなったあなたへ『詳細編』

『詳細編』は『ざっくり編』と説明された内容を、より詳しく・より正確に理解するための助けになる記事となっております。（有料記事です）

今回解説したように、BSD予想自体は雰囲気だけ触れるだけでもとても楽しいものです。しかしながら、背景知識を深く理解することで、もっと面白く感じることもできるのです。ある程度理解していれば、自分で計算実験することもできますし、最近の研究成果の概要を掴むこともできるようになります。

『詳細編』ではBSD予想の主張に現れるさまざまな用語「楕円曲線」「有理点」「ランク」「L関数」「位数」。これらの用語の背景にある数学的な意味を解きほぐし、BSD予想はなぜ面白いのか、その魅力に迫ります。

ぜひ以下のリンクからご覧いただければと思います。（「note」というサービスを利用しています。）
note.com

『詳細編』の閲覧手順

以下の流れで記事を閲覧することができます。

上記のサイトにアクセスし、購入処理を行います（500円）
するとnote記事の続きに、『詳細編』の記事本体のPDFが添付されているので、ダウンロードして読むことができます

お願い

記事を購入する際は、記事を読みたい気持ち50%、tsujimotterを応援したい気持ち50%ぐらいで購入されることをおすすめします。
今回の有料記事は、私の日曜数学活動の方向性を模索する中での試みであり、あくまで実験的なものとなっています。記事の内容にはできる限り誤りのないよう努めておりますが、私の理解不足により誤りが含まれる可能性もあります。ご理解のうえご購入をお願いいたします。
ご購入後の返金はいたしかねますので、予めご了承ください。

*1:世界初の実用的なプログラム内蔵方式の電子計算機

2020-08-30

任意の素数はレピュニットの素因数に現れる（2, 5を除く）あとダイヤル数

数学整数論循環小数レピュニット

Twitterって本当に面白いなと思うのですが、人々のいろんな発見が流れてくるのです。

私が最近面白いと思ったのは次のツイートです。

「2、5を除く全ての素数は11、111、1111、…の素因数として“周期的に”現れる」ってことに気が付いて、証明できた気がするんだけど、これって素数の研究に役立ったりしないかな。おれが気付ける程度のことだから既に知られているとは思うけど。
— Yukinari (@yukinarioshiro) 2020年8月27日

レピュニットについてはこれまでも何度か記事にまとめてきましたが、このツイートに書かれているような事実は知りませんでした。とても面白いと思いましたので、ぜひ紹介させてください。

レピュニット関連の記事はこちらから：
tsujimotter.hatenablog.com

今回の話はレピュニットだけでなく、「循環小数」や「ダイヤル数」という面白いテーマにも広がる話になっています。よろしければ最後までご覧になってください。

2020-08-24

リーマンの再配列定理を使って級数を「お望みの実数」に収束させよう

数学解析学

今日のテーマは「リーマンの再配列定理」です。「条件収束する実数列の級数は、再配列によって任意の実数に収束させることができる」という主張です。何を言っているかわからないという方にも、これから詳しくは説明していきますのでご安心ください。

無限級数

$\displaystyle \sum_{n = 1}^{\infty} a_n$

が絶対収束するとは、各数列に絶対値をつけた

$\displaystyle \sum_{n = 1}^{\infty} |a_n|$

が収束するということです。名前の通りですね。

対する条件収束とは、無限級数が絶対収束はしないが収束はすることを言います。

たとえば、平方数の逆数の和

$\displaystyle \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + \cdots = \frac{\pi^2}{6} \tag{1}$

は絶対収束しますが、自然数の逆数を足し引きする級数（交代級数）

$\displaystyle \frac{1}{1} - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \cdots = \log 2 \tag{2}$

　
は条件収束します。

後者が条件収束であることは、たとえばこちらの記事の最後に紹介されています：
mathtrain.jp

「なぜ絶対収束か条件収束を気にするのか」と疑問に思った方もいるかもしれませんが、それにはワケがあります。

絶対収束する級数は、足し合わせる順番に関わらず同じ値に収束します。つまり、足し合わせる順番を気にする必要がないわけですね。

一方、条件収束する級数については、足し合わせる順番によって収束する先の値が変わってしまうのです。条件収束はとてもナイーブなのですね。

たとえば、 $\log 2$ に収束する式 $(2)$ の級数ですが、足し合わせる順番を入れ替えて

$\displaystyle 1 + \frac{1}{3} - \frac{1}{2} + \frac{1}{5} + \frac{1}{7} - \frac{1}{4} + \frac{1}{9} + \frac{1}{11} - \frac{1}{6} + \cdots$

のように和をとると、 $\frac{3}{2}\log 2$ に収束してしまいます。（計算は自分で確かめてみるといいでしょう。）

さらに面白いことに、冒頭の「リーマンの再配列定理」によれば、条件収束する級数は（足し合わせる順番を入れ替えることで）任意の実数値に収束させることができるというのです。

これはなんというか、とても非自明な感じがしますよね。なんたって任意の実数値ですから。

正確な主張と証明は、以下の記事にまとまっています。
integers.hatenablog.com

とにかく証明はできるわけです。tsujimotterはこれまで証明をきちんと追ったことがなく、なんとなくよくわからないな、難しそうだなとモヤモヤしていました。

そろそろちゃんと理解したいなと思い、つい先ほど証明を追いかけてみたのですが、思っていたよりスッキリ理解することができました。しかも、よくよく読んでみると、証明の中に任意の実数値に収束させる方法が載っていることに気づきました。

これは面白いかもしれない！　なんたって、好きな実数に収束させることができるのですから！

そんなわけでイントロが長くなりましたが、本日の記事では条件収束する級数をお望みの実数に収束させる手順を紹介したいと思います。

2020-08-21

リーマンの素数公式の導出の概略（Enjoy Mathematics! 寄稿記事の公開）

数学素数ゼータ関数おすすめの記事

ゼータ関数を通して素数のことが理解できてしまうという魔法の公式、これが今日のテーマです。

この公式はtsujimotterが素数に興味を持つきっかけとなったもので、これまでも様々な場所でこの公式の魅力について語ってきました。

たとえば、こちらの講演動画など：
www.youtube.com

$\pi(x)$ を「素数のときだけ一段上がる階段状の関数」とします。一般には素数計数関数と呼ばれるものです。

リーマンの素数公式（あるいはリーマンの明示公式）とは、この $\pi(x)$ の挙動を明示的に表す次の公式のことです：　

$\displaystyle \pi(x) =\sum_{1\leq m\leq \log_2(x)} \frac{\mu(m)}{m} \left( \operatorname{li}(x^{\frac{1}{m}}) - \sum_{\rho} \operatorname{li}(x^{\frac{\rho}{m}}) - \log 2 - \int_{x^{\frac{1}{m}}}^{\infty} \frac{dt}{t(t^2-1) \log t} \right) \tag{1}$