tsujimotterのノートブック

日曜数学者 tsujimotter の「趣味で数学」実践ノート

2変数2次関数の極値問題（平方完成と主軸変換の図形的な意味）

数学 解析学 幾何学

前回の記事の続きです（前回の記事を読まなくても、今回の内容は読むことができます）：
tsujimotter.hatenablog.com

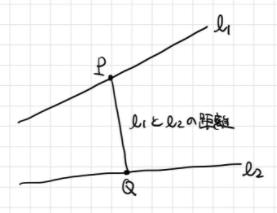
前回の内容を簡単に振り返ります。「空間内の与えられた2直線 l_1, l_2 に対して、その距離を求めることはできるか？」という問題について考えました。 l_1, l_2 からそれぞれ点 P, Q をとったとき、 P, Q の距離は2変数の2次関数関数 F(x, y) として求められます。 F(x, y) の最小値を求めれば、 l_1, l_2 の距離が求まるという話でした。

ここで「2変数の2次関数の最小値はあるのか？」という部分が一つの焦点だったわけですが、 l_1, l_2 が平行でない場合には最小値が極小値に一致する（最小値は存在する）という結論でした。


上の記事では、 F(x, y) を力技で平方完成して最小値を出していました。ところが、ブログ公開後にTwitter上で @Freufirst さんという方から「2次関数の平方完成は合同変換で出来るよ」という旨のアドバイスをいただきました。教えていただいた方法は「まさに」という方法だったのですが、昨日の時点ではまったく頭にありませんでした。ありがとうございます。


というわけで、せっかくなので行列を使った2変数2次関数の極値問題の解法について、詳しくまとめてみたいと思います。2変数2次関数 F(x, y) が極小値（あるいは極大値など）を持つ条件について考察していきたいと思います。

今回は、行列やベクトルとしての式変形を用いてスマートに求めることを目指します。計算の途中では、いくつかの「行列やベクトルの変換操作」を行っていきますが、それらは単なる機械的な置き換えではなく、実はちゃんと図形的な意味があるものになっています。記事の後半では、そのことについても触れていきたいと思います。

続きを読む

空間内の「ねじれの位置」にある2直線間の距離

数学 幾何学

高校数学で習う「空間内の2直線間の距離」について考えてみたいと思います。

3次元空間内に2直線 l_1, l_2 があるとします。 l_1, l_2 が「ねじれの位置にある」とは、 l_1, l_2 が交点を持たず、かつ、平行でもないことを言います。このとき、2直線 l_1, l_2 の距離を考えてみたいと思います。

そもそも2直線の距離とは、というところから考えたいと思います。 l_1 の点 P および l_2 の点 Q を任意にとったとき、距離 PQ の最小値を2直線 l_1, l_2 の距離と定義します。


ここで疑問に思うのは、そもそもこの最小値は存在するのか？、という問題です。2直線の位置関係によっては、2直線のそれぞれの点の距離がいつまでも漸近的に小さくなり続けるなんてこともあるかもしれません。この場合、最小値は存在しないことになります。もちろん、直感的にはそんな状況はなさそうに思えますが、証明される必要があると思います。

最小値が存在しなければ、2直線の距離は定義できない場合が存在するということになってしまいますね。

この記事の最後に述べるように、結果的には最小値は存在し、2直線の距離が定義できます。この事実って高校数学では証明されるのでしょうか？　少なくともtsujimotterはこの証明について聞いた記憶がありませんでした。証明が気になって眠れません。


というわけで、最小値が存在することについて自分なりに考えてみたのがこちらの記事となります。今回は「ベクトル解析」を使った証明ですが、もしかしたら、もっと簡単に考えることもできるかもしれません。

個人的に楽しかったのでまとめてみたという記事になりますので、おおらかな目でみてあげてください。別解などあればお気軽におしらせください。


（追記）
実は最後に書いたのですが、もっとシンプルな解決策があったようです。結果的には、前半で書いたような計算はしなくてもよかったのですが、計算していて楽しかったのでそのまま載せたいと思います。

続きを読む

計算が間違っているのに結果が合っている分数の和 #有害分数

数学 整数論 自由研究・独自研究

一年生の和（freshman sum） というものがあります。

分数の和の計算を計算するときに、通分して計算すべきところを、間違えて

\displaystyle \frac{a}{b} + \frac{c}{d} = \frac{a+c}{b+d} \tag{1}

のように計算してしまうというアレです。

一般に分数の和の計算は難しいものですが、上の式が成り立てば分数の和の計算が楽になるのにな・・・と思うわけです。もちろん、こんな式は一般に成り立たないわけですが、もしかすると上の式が たまたま成り立ってしまうケース が存在するかもしれません。

そんなケースを探してみようというのが今回の記事です。果たして「正しい一年生の和」は存在するのでしょうか？

きっかけ

今回の記事のきっかけは、ポテト一郎さんのこちらの呟きからでした。
togetter.com

面白いですね。上のツイートでは、同様の計算を３つの分数で実行していますが、２つの分数で実行した場合はどうなるかなと思って考えてみたというのが今回の記事になります。

ポテト一郎さんのツイートに関連して、「初学者には有害な分数の計算」の練習プリントを作られた方がいます。

これに対して、私が軽い気持ちで「有害分数」と呼んだところ、 どうもこの名前が定着しているみたいです。#有害分数 というハッシュタグで似たような分数がたくさん投稿されているのでよかったらご覧になってください。

続きを読む

ザリスキー接空間（続・多項式関数に接する多項式関数）

数学 幾何学

前回の記事の続きです。まだ読んでいない方はこちらから。
tsujimotter.hatenablog.com

前回の記事では、 x = p を通る直線を考えて「この直線に x = p で接する関数全体の同値類」を考えて、その同値類全体がザリスキー余接空間 \mathfrak{m}_P/\mathfrak{m}_P^2になっているという話をしました。また、この余接空間の双対空間として、ザリスキー接空間 (\mathfrak{m}_P/\mathfrak{m}_P^2)^* が定義できるよという話もしました。

一方で、ザリスキー接空間については、双対空間を経由せずとも直接的に考えることができるよ、と第二宇宙賢者さんからアドバイスいただきました。

ヒントとして次のPDFを教えていただきましたので、PDFの内容を参考にしつつ、ザリスキー接空間について考えてみたいと思います。

NOTES ON THE ZARISKI TANGENT SPACE
SAM EVENS
https://www3.nd.edu/~sevens/tanspace.pdf


なお、上の記事では一般の多変数の多項式環を元に考えていますが、今回は前回の記事の続きということで、1変数の多項式環に限定して議論したいと思います。また、 \mathbb{R}[x] で考えるのは \mathbb{R} が代数閉体でないゆえの問題（特に極大イデアルに関する問題）がありそうなので、 \mathbb{C}[x] で議論したいと思います。

続きを読む

多項式関数に接する多項式関数（2021年共通テスト数学ⅡB・第2問）

数学 幾何学 自由研究・独自研究

2021年から「センター試験」が「大学入学共通テスト」という名前に代わり、傾向も以前とは変わったということで各所で話題になりましたね。受験生の皆様はお疲れ様でした。

tsujimotterは例年、数学だけは自分で解くようにしているのですが、今年も数学Ⅰ・数学Ａと数学Ⅱ・数学Ｂについて時間制限付きで解いてみました。現役から離れて十数年たっているので、大学合格は難しそうな結果に終わってしまったのですが、いろいろ面白い問題があって解いてみてよかったなと思います。

色々紹介したい問題はたくさんあったのですが、今回考えたいのは数学Ⅱ・数学Ｂの 第２問 です。これについては高校数学の範囲を超えて、色々掘り下げられそうな気がしました。

問題をそのまま掲載するのは気が引けますので、各自検索して確認してください。たとえばこちらのページでは、問題と回答が載っています。まだ解いていない人は自分で考えてみると面白いかもしれません。
edu.chunichi.co.jp

諸注意：
本ブログ記事では共通テストの問題を扱っていますが、日曜数学者 tsujimotter が趣味で勉強した内容を発表するブログ記事であり、受験生向けの解説記事ではありません。

「センター試験の問題を大学以降の数学を使って色々考察してみた」という内容になっていますので、受験に役に立つテクニックといった類のものではないことをあらかじめお伝えしておきます。内容に興味がある受験生の方は「受験の息抜きに」ぐらいの気持ちで読んでいただければと思います。

続きを読む

多様体の「接ベクトル空間」の一歩手前の話

数学 幾何学

最近、多様体に関する勉強をしているのですが「接ベクトル空間」という概念を習得するのに苦労しています。ちょっと抽象的すぎてよくわからないなと思っていたところに、黒木玄さんからの次のツイートが。


というわけで、 \mathbb{R}^3 に埋め込まれた2次元曲面（ 2 つの変数でパラメータ表示された図形）を考えて、その1点 P に接する平面について考えてみましょう。これは多様体そのものではありませんが、実際このような古典的な対象の計算を考えてみることで、多様体の接ベクトル空間がどうしてそのような定義なのか、理解できた気がします！

今回、多様体や多様体の接ベクトル空間の定義は与えませんが、多様体の勉強をしている人はぜひご自身の本の定義と見比べて考えていただければ幸いです。

注意：
今回の記事はtsujimotterが勉強中の内容を自分の言葉でまとめてみたものになります。正しさは保証できませんので、その点にご了承ください。間違っているところなどありましたら、勉強になりますのでご指摘いただければと思います。

続きを読む

（線形代数・復習）双対空間

数学 線形代数

前回の記事：tsujimotter.hatenablog.com

前回に引き続き、線形代数の復習編の記事です。今回は 双対空間 というものを導入したいと思います。


「線形写像を単体で考えるのではなく、全体を考えるとよい」というモチベーションのもと、 V から W への K-線形写像全体のなす K-線形空間 \newcommand{\hom}{\operatorname{Hom}} \hom_K(V, W) を導入しました。

今日は、特に W = K = \mathbb{C} として、線形空間 V から \mathbb{C} への \mathbb{C}-線形写像全体のなす \mathbb{C}-線形空間

V^* = \hom_\mathbb{C}(V, \mathbb{C})

を考えたいと思います。 V^* を V の 双対空間 といいます。ちなみに、 \mathbb{C} の部分は、そのまま \mathbb{R} に置き換えても構いません。「数の集合」への写像であればよいです。

V から \mathbb{C} のような数の集合に対する写像のことを 関数 と言います。 つまり、 V^* は V 上の線形関数全体を表す空間と言えますね。

実は V の双対空間は、前回示したように \mathbb{C}-線形空間になります。関数の値の加法や \mathbb{C} 倍を使って、関数自身の加法や \mathbb{C} 倍を定義すれば良いわけですね。

双対空間 V^* は、 V についての大部分の情報を持っていて、まさに「双対」と呼べる存在になっています。言い換えると「関数を考えると、その土台の空間を考えたことになる」というわけです。


ここでは、次の定理を示したいと思います。

命題（問題3.2 小木曽「代数曲線論」）
V を \mathbb{C}-線形空間とし、 V^* をその双対空間とする。以下 V \neq \{0\} とし、 \{x_1, \ldots, x_n\} を V の基底とする。

このとき、次の (1), (2), (3) が成り立つ：
(1) 次を満たす V 上の関数 f_1, \ldots, f_n \colon V \to \mathbb{C} が一意的に存在する：

\begin{matrix} f_1(x_1) = 1, & \ldots, & f_n(x_n) = 0, \\ \vdots & \ddots & \vdots \\ f_n(x_1) = 0, & \ldots, & f_n(x_n) = 1 \end{matrix}
（対角の値が 1、それ以外の値は 0 であるような写像）
(2) \{f_1, \ldots, f_n \} は V^* の基底をなす。特に \operatorname{dim} V = \operatorname{dim} V^* である。
(3) 写像
\begin{align} \iota\colon V \; &\longrightarrow \;\;\; (V^*)^*, \\ x \; &\longmapsto \; ( f \mapsto f(x) ) \end{align}

は同型写像である。


では、証明しましょう。

続きを読む