循環小数(1): フェルマーの小定理 - tsujimotterのノートブック

循環小数問題

1/12377の小数点以下6193桁目は何か？（問題編） - tsujimotterのノートブック
 1/12377の小数点以下6193桁目は何か？（解答編） - tsujimotterのノートブック

解説編

第１回：循環小数(1): フェルマーの小定理 - tsujimotterのノートブック
第２回：循環小数(2): Midyの定理（前編） - tsujimotterのノートブック
第３回：循環小数(3): Midyの定理（後編） - tsujimotterのノートブック
第４回：循環小数(4): 平方剰余の相互法則 - tsujimotterのノートブック

本記事は、循環小数問題の解説編として書いています。

解説編の第１回では

循環小数は (p-1) 桁で循環する

という基本的な事実について紹介します。

具体例と用語の確認

たとえば、1/7 を考えてみましょう。

1/7 は計算すると次のようになります。

1/7 = 0.142857142857142857...

いつまでたっても続いていきますが、よくみると "142857" が繰り返し並んでいることがわかります。

すなわち、1/7 は循環小数です。

循環する繰り返しのパターン "142857" を循環節と呼びます。

この場合の循環節の長さは 6 です。

循環小数をすべて書くことは出来ないため、次のように最初と最後にドットをつけた１つの循環節によって表記されることが多いです。

$1/7 = 0.\dot{1}4285\dot{7}$

一方、1/2, 1/5 では、循環しないで途中で止まってしまいます。これを有限小数と呼んだりするそうです。

1/2 = 0.5
1/5 = 0.2

一般に、2, 5 以外のすべての素数に対して、1/p は循環小数となることが知られています。

1/p の循環小数は (p-1) 桁目で必ず循環する（本題）

ところで、循環節の長さは、計算してみるとわかりますが長くなったり短くなったりしますね。

たとえば、

$1/11 = 0.\dot{0}\dot{9}$

のように短くなることもあれば、

$1/17 = 0.\dot{0}58823529411764\dot{7}$

のように非常に長くなることもあります。

一見すると循環のパターンは一般性がないように見えます。

しかしながら、pが素数の場合、p=2, 5 以外のどんな 1/p をとっても、小数点以下 (p-1) 桁で必ず循環することが示せます。

次の図は、2, 5 以外の素数 p に対して、循環節と循環のパターンを示したものです。

f:id:tsujimotter:20140405195035p:plain

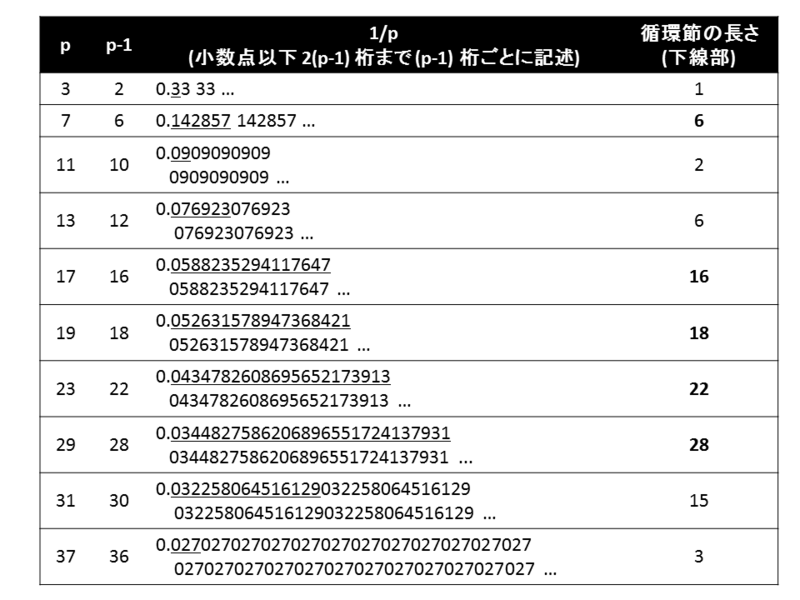
下線部は循環節ですが、循環節の長さに関わらず小数点以下 (p-1) 桁目でたしかに循環していることがわかります。

循環節の定義から、循環節の長さの倍数の桁で繰り返しがおきます。したがって、循環節の長さが (p-1) の約数であることもわかってしまいます。

このことは、2, 5 以外の素数すべてで一般に成り立ちます！

《定理１》
$p$ を $2$ , $5$ 以外の素数としたとき、循環小数 $1/p$ は $(p-1)$ 桁で循環する。また、その循環節の長さは $(p-1)$ の約数となる。

面白いですね。でも、本当にちゃんと (p-1)桁で循環は起きるのでしょうか。

以降で、《定理１》を証明することにしましょう。

フェルマーの小定理

まず、この証明で使う 《フェルマーの小定理》 について紹介します。
非常に重要な公式で、整数論で頻発する式なので、知らない方はこれを機に覚えるとよいかと思います。

《フェルマーの小定理》
$p$ を素数とし、 $a$ を $p$ と互いに素な整数としたとき、次の合同式が成り立つ。

$a^{p-1} \equiv 1 \pmod p$

$a=10$ , $p=7$ として考えてみましょう。

$10^{1} \equiv 3 \pmod 7$
$10^{2} \equiv 2 \pmod 7$
$10^{3} \equiv 6 \pmod 7$
$10^{4} \equiv 4 \pmod 7$
$10^{5} \equiv 5 \pmod 7$
$10^{6} \equiv 1 \pmod 7$

実際に、 $10^{6} \equiv 1 \pmod 7$ となることがわかります。

証明

p を素数としたとき、循環小数 1/p は (p-1) 桁で循環することを証明する。

まず循環小数 $1/p$ を次のように表し、 $e$ 桁で循環するとします。小数点以下 $e$ 桁までの循環パターンの数を $c$ とします。

$\displaystyle \frac{1}{p} = \frac{c}{10^e}+\frac{c}{10^{2e}}+\frac{c}{10^{3e}}+\cdots$

これを以下のように変形していきます。

$\displaystyle \begin{eqnarray} \frac{1}{p} &=& \frac{c}{10^e}+\frac{c}{10^{2e}}+\frac{c}{10^{3e}}+\cdots \\ &=& \frac{c}{10^e}\left(1+\frac{1}{10^{e}}+\frac{1}{10^{2e}}+\cdots\right) \\ &=& \frac{c/10^e}{1-1/10^e} \\ &=& \frac{c}{10^e-1} \end{eqnarray}$

したがって、